|
CGAL 4.14 - 3D Polyhedral Surface
|
|
CGAL 4.14 - 3D Polyhedral Surface
|
Polyhedral surfaces in three dimensions are composed of vertices, edges, facets and an incidence relationship on them. The organization beneath is a halfedge data structure, which restricts the class of representable surfaces to orientable 2-manifolds - with and without boundary. If the surface is closed we call it a polyhedron, for example, see the following model of a hammerhead:
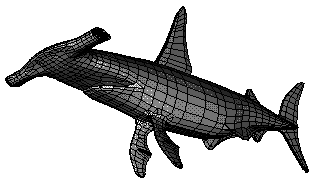
The polyhedral surface is realized as a container class that manages vertices, halfedges, facets with their incidences, and that maintains the combinatorial integrity of them. It is based on the highly flexible design of the halfedge data structure, see the introduction in Chapter Halfedge Data Structures and [3]. However, the polyhedral surface can be used and understood without knowing the underlying design. Some of the examples in this chapter introduce also gradually into first applications of this flexibility.
A polyhedral surface Polyhedron_3<PolyhedronTraits_3> in three dimensions consists of vertices V, edges E, facets F and an incidence relation on them. Each edge is represented by two halfedges with opposite orientations. The incidences stored with a halfedge are illustrated in the following figure:
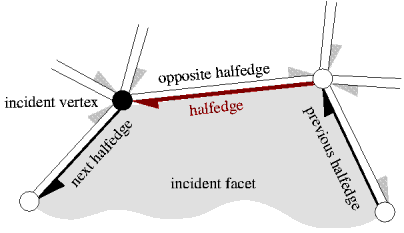
Vertices represent points in space. Edges are straight line segments between two endpoints. Facets are planar polygons without holes. Facets are defined by the circular sequence of halfedges along their boundary. The polyhedral surface itself can have holes (with at least two facets surrounding it since a single facet cannot have a hole). The halfedges along the boundary of a hole are called border halfedges and have no incident facet. An edge is a border edge if one of its halfedges is a border halfedge. A surface is closed if it contains no border halfedges. A closed surface is a boundary representation for polyhedra in three dimensions. The convention is that the halfedges are oriented counterclockwise around facets as seen from the outside of the polyhedron. An implication is that the halfedges are oriented clockwise around the vertices. The notion of the solid side of a facet as defined by the halfedge orientation extends to polyhedral surfaces with border edges although they do not define a closed object. If normal vectors are considered for the facets, normals point outwards (following the right-hand rule).
The strict definition can be found in [3]. One implication of this definition is that the polyhedral surface is always an orientable and oriented 2-manifold with border edges, i.e., the neighborhood of each point on the polyhedral surface is either homeomorphic to a disc or to a half disc, except for vertices where many holes and surfaces with boundary can join. Another implication is that the smallest representable surface avoiding self intersections is a triangle (for polyhedral surfaces with border edges) or a tetrahedron (for polyhedra). Boundary representations of orientable 2-manifolds are closed under Euler operations. They are extended with operations that create or close holes in the surface.
Other intersections besides the incidence relation are not allowed. However, this is not automatically verified in the operations, since self intersections are not easy to check efficiently. Polyhedron_3<PolyhedronTraits_3> does only maintain the combinatorial integrity of the polyhedral surface (using Euler operations) and does not consider the coordinates of the points or any other geometric information.
Polyhedron_3<PolyhedronTraits_3> can represent polyhedral surfaces as well as polyhedra. The interface is designed in such a way that it is easy to ignore border edges and work only with polyhedra.
The polyhedral surface is based on the highly flexible design of the halfedge data structure. Examples for this flexibility can be found in Section Extending Vertices, Halfedges, and Facets and in Section Examples of the chapter on the halfedge data structure. This design is not a prerequisite to understand the following examples. See also the Section sectionPolyAdvanced below for some advanced examples.
The first example instantiates a polyhedron using a kernel as traits class. It creates a tetrahedron and stores the reference to one of its halfedges in a Halfedge_handle. Handles, also know as trivial iterators, are used to keep references to halfedges, vertices, or facets for future use. There is also a Halfedge_iterator type for enumerating halfedges. Such an iterator type can be used wherever a handle is required. Respective Halfedge_const_handle and Halfedge_const_iterator for a constant polyhedron and similar handles and iterators with Vertex_ and Facet_ prefix are provided too.
The example continues with a test if the halfedge actually refers to a tetrahedron. This test checks the connected component referred to by the halfedge h and not the polyhedral surface as a whole. This examples works only on the combinatorial level of a polyhedral surface. The next example adds the geometry.
File Polyhedron/polyhedron_prog_simple.cpp
We add geometry to the our construction of a tetrahedron. Four points are passed as arguments to the construction. This example demonstrates in addition the use of the vertex iterator and the access to the point in the vertices. Note the natural access notation v->point(). Similarly, all information stored in a vertex, halfedge, and facet can be accessed with a member function given a handle or iterator. For example, given a halfedge handle h we can write h->next() to get a halfedge handle to the next halfedge, h->opposite() for the opposite halfedge, h->vertex() for the incident vertex at the tip of h, and so on. The output of the program will be
1 0 0 0 1 0 0 0 1 0 0 0
File Polyhedron/polyhedron_prog_tetra.cpp
The polyhedron offers a point iterator for convenience. The above for loop simplifies to a single statement by using std::copy and the ostream iterator adaptor.
An affine transformation A can act as a functor transforming points and a point iterator is conveniently defined for polyhedral surfaces. So, assuming we want only the point coordinates of a polyhedron P transformed, std::transform does the job in a single line.
The polyhedral surface has already provisions to store a plane equation for each facet. However, it does not provide a function to compute plane equations.
This example computes the plane equations of a polyhedral surface. The actual computation is implemented in the Plane_equation functor. Depending on the arithmetic (exact/inexact) and the shape of the facets (convex/non-convex) different methods are useful. We assume here strictly convex facets and exact arithmetic. In our example a homogeneous representation with int coordinates is sufficient. The four plane equations of the tetrahedron are the output of the program.
File Polyhedron/polyhedron_prog_planes.cpp
The polyhedron class template has actually four parameters, where three of them have default values. Using the default values explicitly in our examples above for three parameter - ignoring the fourth parameter, which would be a standard allocator for container class - the definition of a polyhedron looks like:
The Polyhedron_items_3 class contains the types used for vertices, edges, and facets. The HalfedgeDS_default class defines the halfedge data structure used, which is a list-based representation in this case. An alternative is a vector-based representation. Using a vector provides random access for the elements in the polyhedral surface and is more space efficient, but elements cannot be deleted arbitrarily. Using a list allows arbitrary deletions, but provides only bidirectional iterators and is less space efficient. The following example creates again a tetrahedron with given points, but in a vector-based representation.
The vector-based representation resizes automatically if the reserved capacity is not sufficient for the new items created. Upon resizing all handles, iterators, and circulators become invalid. Their correct update in the halfedge data structure is costly, thus it is advisable to reserve enough space in advance as indicated with the alternative constructor in the comment.
Note that the polyhedron and not the underlying halfedge data structure triggers the resize operation, since the resize operation requires some preconditions, such as valid incidences, to be fulfilled that only the polyhedron can guarantee.
File Polyhedron/polyhedron_prog_vector.cpp
We create a tetrahedron and write it to std::cout using the Object File Format (OFF) [5]. This example makes use of STL algorithms (std::copy, std::distance), STL std::ostream_iterator, and CGAL circulators. The polyhedral surface provides convenient circulators for the counterclockwise circular sequence of halfedges around a facet and the clockwise circular sequence of halfedges around a vertex.
However, the computation of the vertex index in the inner loop of the facet output is not advisable with the std::distance function, since it takes linear time for non random-access iterators, which leads to quadratic runtime. For better runtime the vertex index needs to be stored separately and computed once before writing the facets. It can be stored, for example, in the vertex itself or in a hash-structure. See also Section File I/O.
File Polyhedron/polyhedron_prog_off.cpp
Euler operators are the natural way of modifying polyhedral surfaces. We provide a set of operations for polyhedra: split_facet(), join_facet(), split_vertex(), join_vertex(), split_loop(), and join_loop(). We add further convenient operators, such as split_edge(). However, they could be implemented using the six operators above. Furthermore, we provide more operators to work with polyhedral surfaces with border edges, for example, creating and deleting holes. We refer to the references manual for the definition and illustrative figures of the Euler operators.
The following example implements a function that appends a unit cube to a polyhedral surface. To keep track of the different steps during the creation of the cube a sequence of sketches might help with labels for the different handles that occur in the program code. The following Figure shows six selected steps from the creation sequence. These steps are also marked in the program code.
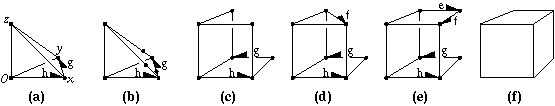
File Polyhedron/polyhedron_prog_cube.cpp
A polyhedron can be visualized by calling the CGAL::draw() function as shown in the following example. This function opens a new window showing the given polyhedron. The function is blocking, that is the program continues as soon as the user closes the window.
File Polyhedron/draw_polyhedron.cpp
This function requires CGAL_Qt5, and is only available if the flag CGAL_USE_BASIC_VIEWER is defined at compile time.

Simple file I/O for polyhedral surfaces is already provided in the library. The file I/O considers so far only the topology of the surface and its point coordinates. It ignores a possible plane equation or any user-added attributes, such as color.
The default file format supported in CGAL for output as well as for input is the Object File Format, OFF, with file extension .off, which is also understood by Geomview [5]. For OFF an ASCII and a binary format exist. The format can be selected with the CGAL modifiers for streams, set_ascii_mode() and set_binary_mode() respectively. The modifier set_pretty_mode() can be used to allow for (a few) structuring comments in the output. Otherwise, the output would be free of comments. The default for writing is ASCII without comments. Both, ASCII and binary format, can be read independent of the stream setting. Since this file format is the default format, iostream operators are provided for it.
Additional formats supported for writing are OpenInventor (.iv) [7], VRML 1.0 and 2.0 (.wrl) [1], [6], [2], and Wavefront Advanced Visualizer object format (.obj). Another convenient output function writes a polyhedral surface to a Geomview process spawned from the CGAL program. These output functions are provided as stream operators, now acting on the stream type of the respective format.
All these file formats have in common that they represent a surface as a set of facets. Each facet is a list of indices pointing into a set of vertices. Vertices are represented as coordinate triples. The file I/O for polyhedral surfaces Polyhedron_3 imposes certain restrictions on these formats. They must represent a permissible polyhedral surface, e.g., a 2-manifold and no isolated vertices, see Section Introduction.
Some example programs around the different file formats are provided in the distribution under examples/Polyhedron_IO/ and demo/Polyhedron_IO/. We show an example converting OFF input into VRML 1.0 output.
File Polyhedron_IO/polyhedron2vrml.cpp
In Section Example with a Vector Instead of a List Representation we have seen how to change the default list representation
to a vector based representation of the underlying halfedge data structure. Now we want to look a bit closer at the second template argument, Polyhedron_items_3, that specifies what kind of vertex, halfedge, and facet is used. The implementation of Polyhedron_items_3 looks a bit involved with nested wrapper class templates. But ignoring this technicality, what remains are three local typedefs that define the Vertex, the Halfedge, and the Face for the polyhedral surface. Note that we use here Face instead of facet. Face is the term used for the halfedge data structure. Only the top layer of the polyhedral surface gives alias names renaming face to facet.
If we look up in the reference manual the definitions of the three classes used in the typedefs, we will see the confirmation that the default polyhedron uses all supported incidences, a point in the vertex class, and a plane equation in the face class. Note how the wrapper class provides two template parameters, Refs, which we discuss a bit later, and Traits, which is the geometric traits class used by the polyhedral surface and which provides us here with the types for the point and the plane equation.
Using this example code we can write our own items class. Instead, we illustrate an easier way if we only want to exchange one class. We use a simpler face without the plane equation but with a color attribute added. To simplify the creation of a vertex, halfedge, or face class, it is always recommended to derive from one of the given base classes. Even if the base class would contain no data it would provide convenient type definitions. So, we derive from the base class, repeat the mandatory constructors if necessary - which is not the case for faces but would be for vertices - and add the color attribute.
The new items class is derived from the old items class and the wrapper containing the face typedef gets overridden. Note that the name of the wrapper and its template parameters are fixed. They cannot be changed even if, as in this example, a template parameter is not used.
When we use our new items class with the polyhedral surface, our new face class is used in the halfedge data structure and the color attribute is available in the type Polyhedron_3::Facet. However, Polyhedron_3::Facet is not the same type as our local face typedef for My_face, but it is derived therefrom. Thus, everything that we put in the local face type except constructors is then available in the Polyhedron_::Facet type. For more details, see the Chapter Halfedge Data Structures on the halfedge data structure design.
Pulling all pieces together, the full example program illustrates how easy the color attribute can be accessed once it is defined.
File Polyhedron/polyhedron_prog_color.cpp
We come back to the first template parameter, Refs, of the wrapper classes. This parameter provides us with local types that allow us to make further references between vertices, halfedges, and facets, which have not already been prepared for in the current design. These local types are Polyhedron_3::Vertex_handle, Polyhedron_3::Halfedge_handle, Polyhedron_3::Facet_handle, and there respective .._const_handle. We add now a new vertex reference to a face class as follows. Encapsulation and access functions could be added for a more thorough design, but we omit that here for the sake of brevity. The integration of the face class with the items class works as illustrated above.
More advanced examples can be found in the Section sectionHdsExamples illustrating further the design of the halfedge data structure.
This program reads a polyhedral surface from the standard input and writes a refined polyhedral surface to the standard output. Input and output are in the Object File Format, OFF, with the common file extension .off, which is also understood by Geomview [5].
The refinement is a single step of the \( \sqrt{3}\)-scheme for creating a subdivision surface [4]. Each step subdivides a facet into triangles around a new center vertex, smoothes the position of the old vertices, and flips the old edges. The program is organized along this outline. In each of these parts, the program efficiently uses the knowledge that the newly created vertices, edges, and facets have been added to the end of the sequences. The program needs additional processing memory only for the smoothing step of the old vertices.
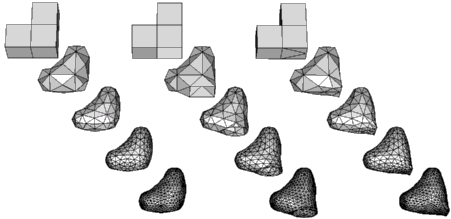
The above figure shows three example objects, each subdivided four times. The initial object for the left sequence is the closed surface of three unit cubes glued together to a corner. The example program shown here can handle only closed surfaces, but the extended example examples/Polyhedron/polyhedron_prog_subdiv_with_boundary.cpp handles surfaces with boundary. So, the middle sequence starts with the same surface where one of the facets has been removed. The boundary subdivides to a nice circle. The third sequence creates a sharp edge using a trick in the object presentation. The sharp edge is actually a hole whose vertex coordinates pinch the hole shut to form an edge. The example directory examples/Polyhedron/ contains the OFF files used here.
File Polyhedron/polyhedron_prog_subdiv.cpp
A utility class Polyhedron_incremental_builder_3 helps in creating polyhedral surfaces from a list of points followed by a list of facets that are represented as indices into the point list. This is particularly useful for implementing file reader for common file formats. It is used here to create a triangle.
A modifier mechanism allows to access the internal representation of the polyhedral surface, i.e., the halfedge data structure, in a controlled manner. A modifier is basically a callback mechanism using a function object. When called, the function object receives the internal halfedge data structure as a parameter and can modify it. On return, the polyhedron can check the halfedge data structure for validity. Such a modifier object must always return with a halfedge data structure that is a valid polyhedral surface. The validity check is implemented as an expensive postcondition at the end of the Polyhedron_3::delegate() member function, i.e., it is not called by default, only when expensive checks are activated.
In this example, Build_triangle is such a function object derived from Modifier_base<HalfedgeDS>. The Polyhedron_3::delegate() member function of the polyhedron accepts this function object and calls its Modifier_base::operator()() with a reference to its internally used halfedge data structure. Thus, this member function in Build_triangle can create the triangle in the halfedge data structure.
File Polyhedron/polyhedron_prog_incr_builder.cpp