|
CGAL 4.6.1 - Polynomial
|
|
CGAL 4.6.1 - Polynomial
|
Functions | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Canonicalize::result_type | CGAL::canonicalize (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Compare::result_type | CGAL::compare (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Degree::result_type | CGAL::degree (const Polynomial_d &p, int i, index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Degree_vector::result_type | CGAL::degree_vector (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Differentiate::result_type | CGAL::differentiate (const Polynomial_d &p, index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Evaluate_homogeneous::result_type | CGAL::evaluate_homogeneous (const Polynomial_d &p, Polynomial_traits_d< Polynomial_d >::Coefficient_type u, Polynomial_traits_d< Polynomial_d >::Coefficient_type v) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Evaluate::result_type | CGAL::evaluate (const Polynomial_d &p, Polynomial_traits_d< Polynomial_d >::Coefficient_type x) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Gcd_up_to_constant_factor::result_type | CGAL::gcd_up_to_constant_factor (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::get_coefficient::result_type | CGAL::get_coefficient (const Polynomial_d &p, int i) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::get_innermost_coefficient::result_type | CGAL::get_innermost_coefficient (const Polynomial_d &p, Exponent_vector ev) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Innermost_leading_coefficient::result_type | CGAL::innermost_leading_coefficient (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Integral_division_up_to_constant_factor::result_type | CGAL::integral_division_up_to_constant_factor (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Invert::result_type | CGAL::invert (const Polynomial_d &p, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Is_square_free::result_type | CGAL::is_square_free (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class InputIterator > | |
| Polynomial_traits_d < Polynomial_d > ::Is_zero_at_homogeneous::result_type | CGAL::is_zero_at_homogeneous (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class InputIterator > | |
| Polynomial_traits_d < Polynomial_d > ::Is_zero_at::result_type | CGAL::is_zero_at (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Leading_coefficient::result_type | CGAL::leading_coefficient (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Make_square_free::result_type | CGAL::make_square_free (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Move::result_type | CGAL::move (const Polynomial_d &p, int i, int j) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Multivariate_content::result_type | CGAL::multivariate_content (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Negate::result_type | CGAL::negate (const Polynomial_d &p, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<typename Polynomial_d > | |
| int | CGAL::number_of_real_roots (Polynomial_d f) |
| computes the number of distinct real roots of \(f\). More... | |
| template<typename InputIterator > | |
| int | CGAL::number_of_real_roots (InputIterator start, InputIterator end) |
| computes the number of distinct real roots of \( f\) whose principal Sturm-Habicht coefficients are passed by the iterator range. More... | |
| template<class Polynomial_d , class InputIterator > | |
| Polynomial_traits_d < Polynomial_d > ::Permute::result_type | CGAL::permute (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<typename Polynomial_d , typename OutputIterator > | |
| OutputIterator | CGAL::polynomial_subresultants (Polynomial_d p, Polynomial_d q, OutputIterator out) |
| computes the polynomial subresultants of \( p\) and \( q\), with respect to the outermost variable. More... | |
| template<typename Polynomial_d , typename OutputIterator1 , typename OutputIterator2 , typename OutputIterator3 > | |
| OutputIterator1 | CGAL::polynomial_subresultants_with_cofactors (Polynomial_d p, Polynomial_d q, OutputIterator1 sres_out, OutputIterator2 coP_out, OutputIterator3 coQ_out) |
computes the polynomial subresultants of \( p\) and \( q\), sres_out, with respect to the outermost variable, and the cofactors for \( P\), coP_out and \( Q\), coQ_out. More... | |
| template<typename Polynomial_d , typename OutputIterator > | |
| OutputIterator | CGAL::principal_sturm_habicht_sequence (typename Polynomial_d f, OutputIterator out) |
| computes the principal Sturm-Habicht coefficients of \( f\) with respect to the outermost variable. More... | |
| template<typename Polynomial_d , typename OutputIterator > | |
| OutputIterator | CGAL::principal_subresultants (Polynomial_d p, Polynomial_d q, OutputIterator out) |
| computes the principal subresultants of \( p\) and \( q\), with respect to the outermost variable. More... | |
| template<class Polynomial_d > | |
| void | CGAL::pseudo_division (const Polynomial_d &f, const Polynomial_d &g, Polynomial_d &q, Polynomial_d &r, Polynomial_traits_d< Polynomial_d >::Coefficient_type &D) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Pseudo_division_quotient::result_type | CGAL::pseudo_division_quotient (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Pseudo_division_remainder::result_type | CGAL::pseudo_division_remainder (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Resultant::result_type | CGAL::resultant (const Polynomial_d &p, const Polynomial_d &q) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Scale_homogeneous::result_type | CGAL::scale_homogeneous (const Polynomial_d &p, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &u, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &v, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Scale::result_type | CGAL::scale (const Polynomial_d &p, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &a, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Shift::result_type | CGAL::shift (const Polynomial_d &p, int i, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class InputIterator > | |
| Polynomial_traits_d < Polynomial_d > ::Sign_at_homogeneous::result_type | CGAL::sign_at_homogeneous (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class InputIterator > | |
| Polynomial_traits_d < Polynomial_d > ::Sign_at::result_type | CGAL::sign_at (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class OutputIterator > | |
| OutputIterator | CGAL::square_free_factorize (const Polynomial_d &p, OutputIterator it, Polynomial_traits_d< Polynomial >::Innermost_coefficient &a) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class OutputIterator > | |
| OutputIterator | CGAL::square_free_factorize (const Polynomial_d &p, OutputIterator it) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class OutputIterator > | |
| OutputIterator | CGAL::square_free_factorize_up_to_constant_factor (const Polynomial_d &p, OutputIterator it) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<typename Polynomial_d , typename OutputIterator > | |
| OutputIterator | CGAL::sturm_habicht_sequence (Polynomial_d f, OutputIterator out) |
| computes the Sturm-Habicht-sequence of \( f\) with respect to the outermost variable. More... | |
| template<typename Polynomial_d , typename OutputIterator1 , typename OutputIterator2 , typename OutputIterator3 > | |
| OutputIterator1 | CGAL::sturm_habicht_sequence_with_cofactors (Polynomial_d f, OutputIterator1 stha_out, OutputIterator2 cof_out, OutputIterator3 cofx_out) |
computes the Sturm-Habicht sequence of \( f\) stha_out, with respect to the outermost variable, and the cofactors for \( f\), cof_out and \( f'\), cofx_out. More... | |
| template<class Polynomial_d , class InputIterator > | |
| CGAL::Coercion_traits < Polynomial_traits_d < Polynomial_d > ::Innermost_coefficient, std::iterator_traits < Input_iterator >::value_type > ::Type | CGAL::substitute_homogeneous (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d , class InputIterator > | |
| CGAL::Coercion_traits < Polynomial_traits_d < Polynomial_d > ::Innermost_coefficient, std::iterator_traits < Input_iterator >::value_type > ::Type | CGAL::substitute (const Polynomial_d &p, InputIterator begin, InputIterator end) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Swap::result_type | CGAL::swap (const Polynomial_d &p, int i, int j) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Total_degree::result_type | CGAL::total_degree (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Translate_homogeneous::result_type | CGAL::translate_homogeneous (const Polynomial_d &p, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &u, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &v, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Translate::result_type | CGAL::translate (const Polynomial_d &p, const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type &a, int index=Polynomial_traits_d< Polynomial_d >::d-1) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Univariate_content::result_type | CGAL::univariate_content (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| template<class Polynomial_d > | |
| Polynomial_traits_d < Polynomial_d > ::Univariate_content_up_to_constant_factor::result_type | CGAL::univariate_content_up_to_constant_factor (const Polynomial_d &p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>. More... | |
| Polynomial_traits_d<Polynomial_d>::Canonicalize::result_type CGAL::canonicalize | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Canonicalize.
For more details see the concept PolynomialTraits_d::Canonicalize.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Compare::result_type CGAL::compare | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Compare.
For more details see the concept PolynomialTraits_d::Compare.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Degree::result_type CGAL::degree | ( | const Polynomial_d & | p, |
| int | i, | ||
| index | = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Degree.
For more details see the concept PolynomialTraits_d::Degree.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Degree_vector::result_type CGAL::degree_vector | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::DegreeVector.
For more details see the concept PolynomialTraits_d::DegreeVector.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Differentiate::result_type CGAL::differentiate | ( | const Polynomial_d & | p, |
| index | = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Differentiate.
For more details see the concept PolynomialTraits_d::Differentiate.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Evaluate::result_type CGAL::evaluate | ( | const Polynomial_d & | p, |
| Polynomial_traits_d< Polynomial_d >::Coefficient_type | x | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Evaluate.
For more details see the concept PolynomialTraits_d::Evaluate.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Evaluate_homogeneous::result_type CGAL::evaluate_homogeneous | ( | const Polynomial_d & | p, |
| Polynomial_traits_d< Polynomial_d >::Coefficient_type | u, | ||
| Polynomial_traits_d< Polynomial_d >::Coefficient_type | v | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Evaluate_homogeneous.
For more details see the concept PolynomialTraits_d::EvaluateHomogeneous.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Gcd_up_to_constant_factor::result_type CGAL::gcd_up_to_constant_factor | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Gcd_up_to_constant_factor.
For more details see the concept PolynomialTraits_d::GcdUpToConstantFactor.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::get_coefficient::result_type CGAL::get_coefficient | ( | const Polynomial_d & | p, |
| int | i | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::GetCoefficient.
For more details see the concept PolynomialTraits_d::GetCoefficient.
Polynomial_d PolynomialTraits_d PolynomialTraits_d::GetCoefficient PolynomialTraits_d::GetInnermostCoefficient #include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::get_innermost_coefficient::result_type CGAL::get_innermost_coefficient | ( | const Polynomial_d & | p, |
| Exponent_vector | ev | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::GetInnermostCoefficient.
For more details see the concept PolynomialTraits_d::GetInnermostCoefficient.
Polynomial_d PolynomialTraits_d PolynomialTraits_d::GetCoefficient PolynomialTraits_d::GetInnermostCoefficient #include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Innermost_leading_coefficient::result_type CGAL::innermost_leading_coefficient | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::InnermostLeadingCoefficient.
For more details see the concept PolynomialTraits_d::InnermostLeadingCoefficient.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Integral_division_up_to_constant_factor::result_type CGAL::integral_division_up_to_constant_factor | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Integral_division_up_to_constant_factor.
For more details see the concept PolynomialTraits_d::IntegralDivisionUpToConstantFactor.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Invert::result_type CGAL::invert | ( | const Polynomial_d & | p, |
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Invert.
For more details see the concept PolynomialTraits_d::Invert.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Is_square_free::result_type CGAL::is_square_free | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Is_square_free.
For more details see the concept PolynomialTraits_d::IsSquareFree.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Is_zero_at::result_type CGAL::is_zero_at | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Is_zero_at.
For more details see the concept PolynomialTraits_d::IsZeroAt.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Is_zero_at_homogeneous::result_type CGAL::is_zero_at_homogeneous | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Is_zero_at_homogeneous.
For more details see the concept PolynomialTraits_d::IsZeroAtHomogeneous.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Leading_coefficient::result_type CGAL::leading_coefficient | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Leading_coefficient.
For more details see the concept PolynomialTraits_d::LeadingCoefficient.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Make_square_free::result_type CGAL::make_square_free | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Make_square_free.
For more details see the concept PolynomialTraits_d::MakeSquareFree.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Move::result_type CGAL::move | ( | const Polynomial_d & | p, |
| int | i, | ||
| int | j | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Move.
For more details see the concept PolynomialTraits_d::Move.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Multivariate_content::result_type CGAL::multivariate_content | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Multivariate_content.
For more details see the concept PolynomialTraits_d::MultivariateContent.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Negate::result_type CGAL::negate | ( | const Polynomial_d & | p, |
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Negate.
For more details see the concept PolynomialTraits_d::Negate.
#include <CGAL/polynomial_utils.h>
| int CGAL::number_of_real_roots | ( | Polynomial_d | f) |
computes the number of distinct real roots of \(f\).
Given a polynomial \( f\), or a range of values that is interpreted as the principal Sturm-Habicht coefficients of \( f\), the function computes
\[ m:=\# \{\alpha\in\mathbb{R}\mid f(\alpha)=0\} \]
that is, the number of distinct real roots of \( f\).
The coefficient type of the polynomial, or the value type of the iterator range, respectively must be a model of RealEmbeddable. In the second version, it is not required to pass the exact princiapl Sturm-Habicht coefficients to the functions; it is only required that the sign of each element corresponds to the sign of the actual principal Sturm-Habicht coefficient.
We explain the internals of this function. For a sequence \( I:=(a_0,\ldots,a_n)\) of real numbers with \( a_0\neq 0\), define
\[ C(I)=\ccSum{i=1}{s}\epsilon_i \]
where \( s\) is the number of subsequences of \( I\) of the form
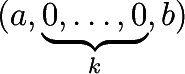
with \( a\neq 0,b\neq 0, k\geq 0\).
For the \( i\)-th subsequence of \( I\), define
\[ \epsilon_i:=\begin{array}{cc} 0 & \mbox{if $k$ is odd},\\ (-1)^{k/2}\mathrm{sign}(ab) & \mbox{if $k$ is even}. \end{array} \]
For \( f\in\mathbb{R}[x]\) with \( \deg f=n\), we have:
\[ C(\mathrm{stha}_n(f),\ldots,\mathrm{stha}_0(f)) = \#\{\alpha\in\R\mid f(\alpha)=0\} \]
In other words, the signs of the principal Sturm-Habicht coefficients determine the number of distinct real roots of \( f\).
#include <CGAL/polynomial_utils.h>
| int CGAL::number_of_real_roots | ( | InputIterator | start, |
| InputIterator | end | ||
| ) |
computes the number of distinct real roots of \( f\) whose principal Sturm-Habicht coefficients are passed by the iterator range.
Given a polynomial \( f\), or a range of values that is interpreted as the principal Sturm-Habicht coefficients of \( f\), the function computes
\[ m:=\# \{\alpha\in\mathbb{R}\mid f(\alpha)=0\} \]
that is, the number of distinct real roots of \( f\).
The coefficient type of the polynomial, or the value type of the iterator range, respectively must be a model of RealEmbeddable. In the second version, it is not required to pass the exact princiapl Sturm-Habicht coefficients to the functions; it is only required that the sign of each element corresponds to the sign of the actual principal Sturm-Habicht coefficient.
We explain the internals of this function. For a sequence \( I:=(a_0,\ldots,a_n)\) of real numbers with \( a_0\neq 0\), define
\[ C(I)=\ccSum{i=1}{s}\epsilon_i \]
where \( s\) is the number of subsequences of \( I\) of the form
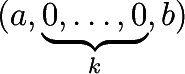
with \( a\neq 0,b\neq 0, k\geq 0\).
For the \( i\)-th subsequence of \( I\), define
\[ \epsilon_i:=\begin{array}{cc} 0 & \mbox{if $k$ is odd},\\ (-1)^{k/2}\mathrm{sign}(ab) & \mbox{if $k$ is even}. \end{array} \]
For \( f\in\mathbb{R}[x]\) with \( \deg f=n\), we have:
\[ C(\mathrm{stha}_n(f),\ldots,\mathrm{stha}_0(f)) = \#\{\alpha\in\R\mid f(\alpha)=0\} \]
In other words, the signs of the principal Sturm-Habicht coefficients determine the number of distinct real roots of \( f\).
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Permute::result_type CGAL::permute | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Permute.
For more details see the concept PolynomialTraits_d::Permute.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::polynomial_subresultants | ( | Polynomial_d | p, |
| Polynomial_d | q, | ||
| OutputIterator | out | ||
| ) |
computes the polynomial subresultants of \( p\) and \( q\), with respect to the outermost variable.
Each element is of type Polynomial_d.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::PolynomialSubresultants.
#include <CGAL/polynomial_utils.h>
| OutputIterator1 CGAL::polynomial_subresultants_with_cofactors | ( | Polynomial_d | p, |
| Polynomial_d | q, | ||
| OutputIterator1 | sres_out, | ||
| OutputIterator2 | coP_out, | ||
| OutputIterator3 | coQ_out | ||
| ) |
computes the polynomial subresultants of \( p\) and \( q\), sres_out, with respect to the outermost variable, and the cofactors for \( P\), coP_out and \( Q\), coQ_out.
The elements of each output range are of type Polynomial_d.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::PolynomialSubresultantsWithCofactors.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::principal_sturm_habicht_sequence | ( | typename Polynomial_d | f, |
| OutputIterator | out | ||
| ) |
computes the principal Sturm-Habicht coefficients of \( f\) with respect to the outermost variable.
Each element is of type Polynomial_traits_d::Coefficient_typeb.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::PrincipalSturmHabichtSequence.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::principal_subresultants | ( | Polynomial_d | p, |
| Polynomial_d | q, | ||
| OutputIterator | out | ||
| ) |
computes the principal subresultants of \( p\) and \( q\), with respect to the outermost variable.
Each element is of type Polynomial_traits_d::Coefficient_type.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::PrincipalSubresultants.
#include <CGAL/polynomial_utils.h>
| void CGAL::pseudo_division | ( | const Polynomial_d & | f, |
| const Polynomial_d & | g, | ||
| Polynomial_d & | q, | ||
| Polynomial_d & | r, | ||
| Polynomial_traits_d< Polynomial_d >::Coefficient_type & | D | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Pseudo_division.
For more details see the concept PolynomialTraits_d::PseudoDivision.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Pseudo_division_quotient::result_type CGAL::pseudo_division_quotient | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Pseudo_division_quotient.
For more details see the concept PolynomialTraits_d::PseudoDivisionQuotient.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Pseudo_division_remainder::result_type CGAL::pseudo_division_remainder | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Pseudo_division_remainder.
For more details see the concept PolynomialTraits_d::PseudoDivisionRemainder.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Resultant::result_type CGAL::resultant | ( | const Polynomial_d & | p, |
| const Polynomial_d & | q | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Resultant.
For more details see the concept PolynomialTraits_d::Resultant.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Scale::result_type CGAL::scale | ( | const Polynomial_d & | p, |
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | a, | ||
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Scale.
For more details see the concept PolynomialTraits_d::Scale.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Scale_homogeneous::result_type CGAL::scale_homogeneous | ( | const Polynomial_d & | p, |
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | u, | ||
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | v, | ||
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Scale_homogeneous.
For more details see the concept PolynomialTraits_d::ScaleHomogeneous.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Shift::result_type CGAL::shift | ( | const Polynomial_d & | p, |
| int | i, | ||
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Shift.
For more details see the concept PolynomialTraits_d::Shift.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Sign_at::result_type CGAL::sign_at | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Sign_at.
For more details see the concept PolynomialTraits_d::SignAt.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Sign_at_homogeneous::result_type CGAL::sign_at_homogeneous | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Sign_at_homogeneous.
For more details see the concept PolynomialTraits_d::SignAtHomogeneous.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::square_free_factorize | ( | const Polynomial_d & | p, |
| OutputIterator | it, | ||
| Polynomial_traits_d< Polynomial >::Innermost_coefficient & | a | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Square_free_factorize.
For more details see the concept PolynomialTraits_d::SquareFreeFactorize.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::square_free_factorize | ( | const Polynomial_d & | p, |
| OutputIterator | it | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Square_free_factorize.
For more details see the concept PolynomialTraits_d::SquareFreeFactorize.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::square_free_factorize_up_to_constant_factor | ( | const Polynomial_d & | p, |
| OutputIterator | it | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Square_free_factorize_up_to_constant_factor.
For more details see the concept PolynomialTraits_d::SquareFreeFactorizeUpToConstantFactor.
#include <CGAL/polynomial_utils.h>
| OutputIterator CGAL::sturm_habicht_sequence | ( | Polynomial_d | f, |
| OutputIterator | out | ||
| ) |
computes the Sturm-Habicht-sequence of \( f\) with respect to the outermost variable.
Each element is of type Polynomial_d.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::SturmHabichtSequence.
#include <CGAL/polynomial_utils.h>
| OutputIterator1 CGAL::sturm_habicht_sequence_with_cofactors | ( | Polynomial_d | f, |
| OutputIterator1 | stha_out, | ||
| OutputIterator2 | cof_out, | ||
| OutputIterator3 | cofx_out | ||
| ) |
computes the Sturm-Habicht sequence of \( f\) stha_out, with respect to the outermost variable, and the cofactors for \( f\), cof_out and \( f'\), cofx_out.
The elements of each output range are of type Polynomial_d.
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
For more details see the concept PolynomialTraits_d::SturmHabichtSequenceWithCofactors.
#include <CGAL/polynomial_utils.h>
| CGAL::Coercion_traits<Polynomial_traits_d<Polynomial_d>::Innermost_coefficient,std::iterator_traits<Input_iterator>::value_type>::Type CGAL::substitute | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Substitute.
For more details see the concept PolynomialTraits_d::Substitute.
#include <CGAL/polynomial_utils.h>
| CGAL::Coercion_traits<Polynomial_traits_d<Polynomial_d>::Innermost_coefficient,std::iterator_traits<Input_iterator>::value_type>::Type CGAL::substitute_homogeneous | ( | const Polynomial_d & | p, |
| InputIterator | begin, | ||
| InputIterator | end | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Substitute_homogeneous.
For more details see the concept PolynomialTraits_d::SubstituteHomogeneous.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Swap::result_type CGAL::swap | ( | const Polynomial_d & | p, |
| int | i, | ||
| int | j | ||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Swap.
For more details see the concept PolynomialTraits_d::Swap.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Total_degree::result_type CGAL::total_degree | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Total_degree.
For more details see the concept PolynomialTraits_d::TotalDegree.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Translate::result_type CGAL::translate | ( | const Polynomial_d & | p, |
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | a, | ||
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Translate.
For more details see the concept PolynomialTraits_d::Translate.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Translate_homogeneous::result_type CGAL::translate_homogeneous | ( | const Polynomial_d & | p, |
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | u, | ||
| const Polynomial_traits_d< Polynomial_d >::Innermost_coefficient_type & | v, | ||
| int | index = Polynomial_traits_d< Polynomial_d >::d-1 |
||
| ) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Translate_homogeneous.
For more details see the concept PolynomialTraits_d::TranslateHomogeneous.
#include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Univariate_content::result_type CGAL::univariate_content | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::UnivariateContent.
For more details see the concept PolynomialTraits_d::UnivariateContent.
Polynomial_d PolynomialTraits_d PolynomialTraits_d::Univariate_Content #include <CGAL/polynomial_utils.h>
| Polynomial_traits_d<Polynomial_d>::Univariate_content_up_to_constant_factor::result_type CGAL::univariate_content_up_to_constant_factor | ( | const Polynomial_d & | p) |
For a given Polynomial_d, adapts the according functor in Polynomial_traits_d<Polynomial_d>.
Adapts Polynomial_traits_d::Univariate_content_up_to_constant_factor.
For more details see the concept PolynomialTraits_d::UnivariateContentUpToConstantFactor.
#include <CGAL/polynomial_utils.h>