#include <CGAL/Triangulation_3.h>

Inherits from

CGAL::Triangulation_utils_3.

Inherited by CGAL::Regular_triangulation_3< Traits, TDS, SLDS >.

Definition

The class Triangulation_3 represents a 3-dimensional tetrahedralization of points.

Template Parameters

Traits	is the geometric traits class and must be a model of `TriangulationTraits_3`.
TDS	is the triangulation data structure and must be a model of `TriangulationDataStructure_3`. `Default` may be used, with default type `Triangulation_data_structure_3<Triangulation_vertex_base_3<Traits>, Triangulation_cell_base_3<Traits> >`. Any custom type can be used instead of `Triangulation_vertex_base_3` and `Triangulation_cell_base_3`, provided that they are models of the concepts `TriangulationVertexBase_3` and `TriangulationCellBase_3`, respectively.
SLDS	is an optional parameter to specify the type of the spatial lock data structure. It must be a model of the `SurjectiveLockDataStructure` concept, with `Object` being a `Point` (as defined below). It is only used if the triangulation data structure used is concurrency-safe (i.e. when `TriangulationDataStructure_3::Concurrency_tag` is `Parallel_tag`). The default value is `Spatial_lock_grid_3<Tag_priority_blocking>` if the triangulation data structure is concurrency-safe, and `void` otherwise. In order to use concurrent operations, the user must provide a reference to a SLDS instance via the constructor or `Triangulation_3::set_lock_data_structure`.

Traversal of the Triangulation

The triangulation class provides several iterators and circulators that allow one to traverse it (completely or partially).

See also: CGAL::Delaunay_triangulation_3; CGAL::Regular_triangulation_3

Examples:: Triangulation_3/for_loop.cpp, Triangulation_3/simple_triangulation_3.cpp, and Triangulation_3/simplex.cpp.

Public Types
enum	Locate_type { VERTEX =0, EDGE, FACET, CELL, OUTSIDE_CONVEX_HULL, OUTSIDE_AFFINE_HULL }
	The enum `Locate_type` is defined by `Triangulation_3` to specify which case occurs when locating a point in the triangulation. More...

Types
The class `Triangulation_3` defines the following types:
typedef Traits	Geom_traits

typedef TDS	Triangulation_data_structure

typedef SLDS	Lock_data_structure

typedef Triangulation_data_structure::Vertex::Point	Point

typedef Geom_traits::Segment_3	Segment

typedef Geom_traits::Triangle_3	Triangle

typedef Geom_traits::Tetrahedron_3	Tetrahedron

Only vertices (0-faces) and cells (3-faces) are stored. Edges (1-faces) and facets (2-faces) are not explicitly represented and thus there are no corresponding classes (see Section Representation).
typedef Triangulation_data_structure::Vertex	Vertex

typedef Triangulation_data_structure::Cell	Cell

typedef Triangulation_data_structure::Facet	Facet

typedef Triangulation_data_structure::Edge	Edge

typedef Triangulation_data_structure::Concurrency_tag	Concurrency_tag
	Concurrency tag (from the TDS).

The vertices and faces of the triangulations are accessed through `handles`, `iterators` and `circulators`. A handle is a model of the `Handle` concept, and supports the two dereference operators and `operator->`. A circulator is a model of the concept `Circulator`. Iterators and circulators are bidirectional and non-mutable. The edges and facets of the triangulation can also be visited through iterators and circulators which are bidirectional and non-mutable. Iterators and circulators are convertible to the corresponding handles, thus the user can pass them directly as arguments to the functions. The handles are also model of the concepts `LessThanComparable` and `Hashable`, that is they can be used as keys in containers such as `std::map` and `boost::unordered_map`.
typedef Triangulation_data_structure::Vertex_handle	Vertex_handle
	handle to a vertex

typedef Triangulation_data_structure::Cell_handle	Cell_handle
	handle to a cell

typedef Triangulation_simplex_3< Self >	Simplex
	Reference to a simplex (vertex, edge, facet or cell) of the triangulation.

typedef Triangulation_data_structure::size_type	size_type
	Size type (an unsigned integral type)

typedef Triangulation_data_structure::difference_type	difference_type
	Difference type (a signed integral type)

typedef Triangulation_data_structure::Cell_iterator	All_cells_iterator
	iterator over cells

typedef Triangulation_data_structure::Facet_iterator	All_facets_iterator
	iterator over facets

typedef Triangulation_data_structure::Edge_iterator	All_edges_iterator
	iterator over edges

typedef Triangulation_data_structure::Vertex_iterator	All_vertices_iterator
	iterator over vertices

typedef unspecified_type	Finite_cells_iterator
	iterator over finite cells

typedef unspecified_type	Finite_facets_iterator
	iterator over finite facets

typedef unspecified_type	Finite_edges_iterator
	iterator over finite edges

typedef unspecified_type	Finite_vertices_iterator
	iterator over finite vertices

typedef unspecified_type	Point_iterator
	iterator over the points corresponding to the finite vertices of the triangulation.

typedef Triangulation_data_structure::Cell_circulator	Cell_circulator
	circulator over all cells incident to a given edge

typedef Triangulation_data_structure::Facet_circulator	Facet_circulator
	circulator over all facets incident to a given edge

In order to write C++ 11 `for`-loops we provide the following range types.
typedef Iterator_range< unspecified_type >	All_cell_handles
	range type for iterating over all cell handles (including infinite cells), with a nested type `iterator` that has as value type `Cell_handle`.

typedef Iterator_range< All_facets_iterator >	All_facets
	range type for iterating over facets.

typedef Iterator_range< All_edges_iterator >	All_edges
	range type for iterating over edges.

typedef Iterator_range< unspecified_type >	All_vertex_handles
	range type for iterating over all vertex handles, with a nested type `iterator` that has as value type `Vertex_handle`.

typedef Iterator_range< unspecified_type >	Finite_cell_handles
	range type for iterating over finite cell handles, with a nested type `iterator` that has as value type `Cell_handle`.

typedef Iterator_range< Finite_facets_iterator >	Finite_facets
	range type for iterating over finite facets.

typedef Iterator_range< Finite_edges_iterator >	Finite_edges
	range type for iterating over finite edges.

typedef Iterator_range< unspecified_type >	Finite_vertex_handles
	range type for iterating over finite vertex handles, with a nested type `iterator` that has as value type `Vertex_handle`.

typedef Iterator_range< unspecified_type >	Points
	range type for iterating over the points of the finite vertices.

Creation
	Triangulation_3 (const Geom_traits &traits=Geom_traits(), Lock_data_structure *lock_ds=nullptr)
	Introduces a triangulation `t` having only one vertex which is the infinite vertex. More...

	Triangulation_3 (Lock_data_structure *lock_ds=nullptr, const Geom_traits &traits=Geom_traits())
	Same as the previous one, but with parameters in reverse order.

	Triangulation_3 (const Triangulation_3 &tr)
	Copy constructor. More...

template<class InputIterator >
	Triangulation_3 (InputIterator first, InputIterator last, const Geom_traits &traits=Geom_traits(), Lock_data_structure *lock_ds=nullptr)
	Equivalent to constructing an empty triangulation with the optional traits class argument and calling `insert(first,last)`.

Assignment
Triangulation_3 &	operator= (const Triangulation_3 &tr)
	The triangulation `tr` is duplicated, and modifying the copy after the duplication does not modify the original. More...

void	swap (Triangulation_3 &tr)
	The triangulations `tr` and `t` are swapped. More...

void	clear ()
	Deletes all finite vertices and all cells of `t`.

template<class GT , class Tds1 , class Tds2 >
bool	operator== (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2)
	Equality operator. More...

template<class GT , class Tds1 , class Tds2 >
bool	operator!= (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2)
	The opposite of `operator==`.

Access Functions
const Geom_traits &	geom_traits () const
	Returns a const reference to the geometric traits object.

const Triangulation_data_structure &	tds () const
	Returns a const reference to the triangulation data structure.

Triangulation_data_structure &	tds ()
	Returns a reference to the triangulation data structure. More...

int	dimension () const
	Returns the dimension of the affine hull.

size_type	number_of_vertices () const
	Returns the number of finite vertices.

size_type	number_of_cells () const
	Returns the number of cells or 0 if `t.dimension() < 3`.

Vertex_handle	infinite_vertex ()
	Returns the infinite vertex.

void	set_infinite_vertex (Vertex_handle v)
	This is an advanced function. More...

Cell_handle	infinite_cell () const
	Returns a cell incident to the infinite vertex.

Non-Constant-Time Access Functions
As previously said, the triangulation is a collection of cells that are either infinite or represent a finite tetrahedra, where an infinite cell is a cell incident to the infinite vertex. Similarly we call an edge (resp. facet) `infinite` if it is incident to the infinite vertex.
size_type	number_of_facets () const
	The number of facets. More...

size_type	number_of_edges () const
	The number of edges. More...

size_type	number_of_finite_cells () const
	The number of finite cells. More...

size_type	number_of_finite_facets () const
	The number of finite facets. More...

size_type	number_of_finite_edges () const
	The number of finite edges. More...

Geometric Access Functions
Tetrahedron	tetrahedron (Cell_handle c) const
	Returns the tetrahedron formed by the four vertices of `c`. More...

Triangle	triangle (Cell_handle c, int i) const
	Returns the triangle formed by the three vertices of facet `(c,i)`. More...

Triangle	triangle (const Facet &f) const
	Same as the previous method for facet `f`. More...

Segment	segment (const Edge &e) const
	Returns the line segment formed by the vertices of `e`. More...

Segment	segment (Cell_handle c, int i, int j) const
	Same as the previous method for edge `(c,i,j)`. More...

const Point &	point (Cell_handle c, int i) const
	Returns the point given by vertex `i` of cell `c`. More...

const Point &	point (Vertex_handle v) const
	Same as the previous method for vertex `v`. More...

Tests for Finite and Infinite Vertices and Faces
bool	is_infinite (Vertex_handle v) const
	`true`, iff vertex `v` is the infinite vertex.

bool	is_infinite (Cell_handle c) const
	`true`, iff `c` is incident to the infinite vertex. More...

bool	is_infinite (Cell_handle c, int i) const
	`true`, iff the facet `i` of cell `c` is incident to the infinite vertex. More...

bool	is_infinite (const Facet &f) const
	`true` iff facet `f` is incident to the infinite vertex. More...

bool	is_infinite (Cell_handle c, int i, int j) const
	`true`, iff the edge `(i,j)` of cell `c` is incident to the infinite vertex. More...

bool	is_infinite (const Edge &e) const
	`true` iff edge `e` is incident to the infinite vertex. More...

Queries
bool	is_vertex (const Point &p, Vertex_handle &v) const
	Tests whether `p` is a vertex of `t` by locating `p` in the triangulation. More...

bool	is_vertex (Vertex_handle v) const
	Tests whether `v` is a vertex of `t`.

bool	is_edge (Vertex_handle u, Vertex_handle v, Cell_handle &c, int &i, int &j) const
	Tests whether `(u,v)` is an edge of `t`. More...

bool	is_facet (Vertex_handle u, Vertex_handle v, Vertex_handle w, Cell_handle &c, int &i, int &j, int &k) const
	Tests whether `(u,v,w)` is a facet of `t`. More...

bool	is_cell (Cell_handle c) const
	Tests whether `c` is a cell of `t`.

bool	is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c, int &i, int &j, int &k, int &l) const
	Tests whether `(u,v,w,x)` is a cell of `t`. More...

bool	is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c) const
	Tests whether `(u,v,w,x)` is a cell of `t` and computes this cell `c`. More...

There is a method `has_vertex()` in the cell class. The analogous methods for facets are defined here.
bool	has_vertex (const Facet &f, Vertex_handle v, int &j) const
	If `v` is a vertex of `f`, then `j` is the index of `v` in the cell `f.first`, and the method returns `true`. More...

bool	has_vertex (Cell_handle c, int i, Vertex_handle v, int &j) const
	Same for facet `(c,i)`. More...

bool	has_vertex (const Facet &f, Vertex_handle v) const

bool	has_vertex (Cell_handle c, int i, Vertex_handle v) const
	Same as the first two methods, but these two methods do not return the index of the vertex.

The following three methods test whether two facets have the same vertices.
bool	are_equal (Cell_handle c, int i, Cell_handle n, int j) const

bool	are_equal (const Facet &f, const Facet &g) const

bool	are_equal (const Facet &f, Cell_handle n, int j) const
	For these three methods: More...

Point Location
The class `Triangulation_3` provides two functions to locate a given point with respect to a triangulation. It provides also functions to test if a given point is inside a finite face or not. Note that the class `Delaunay_triangulation_3` also provides a `nearest_vertex()` function.
Cell_handle	locate (const Point &query, Cell_handle start=Cell_handle(), bool *could_lock_zone=nullptr) const
	If the point `query` lies inside the convex hull of the points, the cell that contains the query in its interior is returned. More...

Cell_handle	locate (const Point &query, Vertex_handle hint, bool *could_lock_zone=nullptr) const
	Same as above but uses `hint` as the starting place for the search.

Cell_handle	inexact_locate (const Point &query, Cell_handle start=Cell_handle()) const
	Same as `locate()` but uses inexact predicates. More...

Cell_handle	locate (const Point &query, Locate_type &lt, int &li, int &lj, Cell_handle start=Cell_handle(), bool *could_lock_zone=nullptr) const
	If `query` lies inside the affine hull of the points, the \( k\)-face (finite or infinite) that contains `query` in its interior is returned, by means of the cell returned together with `lt`, which is set to the locate type of the query (`VERTEX, EDGE, FACET, CELL`, or `OUTSIDE_CONVEX_HULL` if the cell is infinite and `query` lies strictly in it) and two indices `li` and `lj` that specify the \( k\)-face of the cell containing `query`. More...

Cell_handle	locate (const Point &query, Locate_type &lt, int &li, int &lj, Vertex_handle hint, bool *could_lock_zone=nullptr) const
	Same as above but uses `hint` as the starting place for the search.

Bounded_side	side_of_cell (const Point &p, Cell_handle c, Locate_type &lt, int &li, int &lj) const
	Returns a value indicating on which side of the oriented boundary of `c` the point `p` lies. More...

Bounded_side	side_of_facet (const Point &p, const Facet &f, Locate_type &lt, int &li, int &lj) const
	Returns a value indicating on which side of the oriented boundary of `f` the point `p` lies: More...

Bounded_side	side_of_facet (const Point &p, Cell_handle c, Locate_type &lt, int &li, int &lj) const
	Same as the previous method for the facet `(c,3)`.

Bounded_side	side_of_edge (const Point &p, const Edge &e, Locate_type &lt, int &li) const
	Returns a value indicating on which side of the oriented boundary of `e` the point `p` lies: More...

Bounded_side	side_of_edge (const Point &p, Cell_handle c, Locate_type &lt, int &li) const
	Same as the previous method for edge \( (c,0,1)\).

Flips
Two kinds of flips exist for a three-dimensional triangulation. They are reciprocal. To be flipped, an edge must be incident to three tetrahedra. During the flip, these three tetrahedra disappear and two tetrahedra appear. Figure 44.1 (left) shows the edge that is flipped as bold dashed, and one of its three incident facets is shaded. On the right, the facet shared by the two new tetrahedra is shaded. Flips are possible only under the following conditions: - the edge or facet to be flipped is not on the boundary of the convex hull of the triangulation - the five points involved are in convex position. 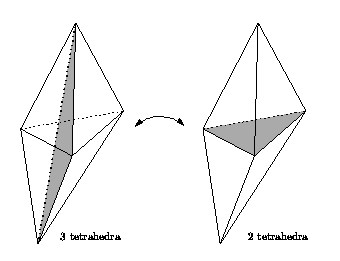Figure 44.1 Flips The following methods guarantee the validity of the resulting 3D triangulation. Flips for a 2d triangulation are not implemented yet.
bool	flip (Edge e)

bool	flip (Cell_handle c, int i, int j)
	Before flipping, these methods check that edge `e=(c,i,j)` is flippable (which is quite expensive). More...

void	flip_flippable (Edge e)

void	flip_flippable (Cell_handle c, int i, int j)
	Should be preferred to the previous methods when the edge is known to be flippable. More...

bool	flip (Facet f)

bool	flip (Cell_handle c, int i)
	Before flipping, these methods check that facet `f=(c,i)` is flippable (which is quite expensive). More...

void	flip_flippable (Facet f)

void	flip_flippable (Cell_handle c, int i)
	Should be preferred to the previous methods when the facet is known to be flippable. More...

Insertions
The following operations are guaranteed to lead to a valid triangulation when they are applied on a valid triangulation.
Vertex_handle	insert (const Point &p, Cell_handle start=Cell_handle())
	Inserts the point `p` in the triangulation and returns the corresponding vertex. More...

Vertex_handle	insert (const Point &p, Vertex_handle hint)
	Same as above but uses `hint` as the starting place for the search.

Vertex_handle	insert (const Point &p, Locate_type lt, Cell_handle loc, int li, int lj)
	Inserts the point `p` in the triangulation and returns the corresponding vertex. More...

template<class PointInputIterator >
std::ptrdiff_t	insert (PointInputIterator first, PointInputIterator last)
	Inserts the points in the range `[first,last)` in the given order, and returns the number of inserted points.

template<class PointWithInfoInputIterator >
std::ptrdiff_t	insert (PointWithInfoInputIterator first, PointWithInfoInputIterator last)
	Inserts the points in the iterator range `[first,last)` in the given order, and returns the number of inserted points. More...

We also provide some other methods that can be used instead of `Triangulatation_3::insert()` when the place where the new point must be inserted is already known. They are also guaranteed to lead to a valid triangulation when they are applied on a valid triangulation.
Vertex_handle	insert_in_cell (const Point &p, Cell_handle c)
	Inserts the point `p` in the cell `c`. More...

Vertex_handle	insert_in_facet (const Point &p, const Facet &f)
	Inserts the point `p` in the facet `f`. More...

Vertex_handle	insert_in_facet (const Point &p, Cell_handle c, int i)
	As above, insertion in the facet `(c,i)`. More...

Vertex_handle	insert_in_edge (const Point &p, const Edge &e)
	Inserts `p` in the edge `e`. More...

Vertex_handle	insert_in_edge (const Point &p, Cell_handle c, int i, int j)
	As above, inserts `p` in the edge \( (i, j)\) of `c`. More...

Vertex_handle	insert_outside_convex_hull (const Point &p, Cell_handle c)
	The cell `c` must be an infinite cell containing `p`. More...

Vertex_handle	insert_outside_affine_hull (const Point &p)
	`p` is linked to all the points, and the infinite vertex is linked to all the points (including `p`) to triangulate the new infinite face, so that all the points now belong to the boundary of the convex hull. More...

template<class CellIt >
Vertex_handle	insert_in_hole (const Point &p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i)
	Creates a new vertex by starring a hole. More...

template<class CellIt >
Vertex_handle	insert_in_hole (const Point &p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i, Vertex_handle newv)
	Same as above, except that `newv` will be used as the new vertex, which must have been allocated previously with e.g. `create_vertex`.

Cell, Face, Edge and Vertex Iterators
The following iterators allow the user to visit cells, facets, edges and vertices of the triangulation. These iterators are non-mutable, bidirectional and their value types are respectively `Cell`, `Facet`, `Edge` and `Vertex`. They are all invalidated by any change in the triangulation.
Finite_vertices_iterator	finite_vertices_begin () const
	Starts at an arbitrary finite vertex. More...

Finite_vertices_iterator	finite_vertices_end () const
	Past-the-end iterator.

Finite_edges_iterator	finite_edges_begin () const
	Starts at an arbitrary finite edge. More...

Finite_edges_iterator	finite_edges_end () const
	Past-the-end iterator.

Finite_facets_iterator	finite_facets_begin () const
	Starts at an arbitrary finite facet. More...

Finite_facets_iterator	finite_facets_end () const
	Past-the-end iterator.

Finite_cells_iterator	finite_cells_begin () const
	Starts at an arbitrary finite cell. More...

Finite_cells_iterator	finite_cells_end () const
	Past-the-end iterator.

All_vertices_iterator	all_vertices_begin () const
	Starts at an arbitrary vertex. More...

All_vertices_iterator	all_vertices_end () const
	Past-the-end iterator.

All_edges_iterator	all_edges_begin () const
	Starts at an arbitrary edge. More...

All_edges_iterator	all_edges_end () const
	Past-the-end iterator.

All_facets_iterator	all_facets_begin () const
	Starts at an arbitrary facet. More...

All_facets_iterator	all_facets_end () const
	Past-the-end iterator.

All_cells_iterator	all_cells_begin () const
	Starts at an arbitrary cell. More...

All_cells_iterator	all_cells_end () const
	Past-the-end iterator.

Point_iterator	points_begin () const
	Iterates over the points of the triangulation.

Point_iterator	points_end () const
	Past-the-end iterator.

Ranges
In order to write C++ 11 `for`-loops we provide a range type and member functions to generate ranges. Note that vertex and cell ranges are special. See Section Iterators and Ranges in the User Manual.
All_cell_handles	all_cell_handles () const
	returns a range of iterators over all cells (even the infinite cells). More...

All_facets	all_facets () const
	returns a range of iterators starting at an arbitrary facet. More...

All_edges	all_edges () const
	returns a range of iterators starting at an arbitrary edge. More...

All_vertex_handles	all_vertex_handles () const
	returns a range of iterators over all vertices (even the infinite one). More...

Finite_cell_handles	finite_cell_handles () const
	returns a range of iterators over finite cells. More...

Finite_facets	finite_facets () const
	returns a range of iterators starting at an arbitrary facet. More...

Finite_edges	finite_edges () const
	returns a range of iterators starting at an arbitrary edge. More...

Finite_vertex_handles	finite_vertex_handles () const
	returns a range of iterators over finite vertices. More...

Points	points () const
	returns a range of iterators over the points of finite vertices.

Cell and Facet Circulators
The following circulators respectively visit all cells or all facets incident to a given edge. They are non-mutable and bidirectional. They are invalidated by any modification of one of the cells traversed.
Cell_circulator	incident_cells (Edge e) const
	Starts at an arbitrary cell incident to `e`. More...

Cell_circulator	incident_cells (Cell_handle c, int i, int j) const
	As above for edge `(i,j)` of `c`.

Cell_circulator	incident_cells (Edge e, Cell_handle start) const
	Starts at cell `start`. More...

Cell_circulator	incident_cells (Cell_handle c, int i, int j, Cell_handle start) const
	As above for edge `(i,j)` of `c`.

The following circulators on facets are defined only in dimension 3, though facets are defined also in dimension 2: there are only two facets sharing an edge in dimension 2.
Facet_circulator	incident_facets (Edge e) const
	Starts at an arbitrary facet incident to `e`. More...

Facet_circulator	incident_facets (Cell_handle c, int i, int j) const
	As above for edge `(i,j)` of `c`.

Facet_circulator	incident_facets (Edge e, Facet start) const
	Starts at facet `start`. More...

Facet_circulator	incident_facets (Edge e, Cell_handle start, int f) const
	Starts at facet of index `f` in `start`.

Facet_circulator	incident_facets (Cell_handle c, int i, int j, Facet start) const
	As above for edge `(i,j)` of `c`.

Facet_circulator	incident_facets (Cell_handle c, int i, int j, Cell_handle start, int f) const
	As above for edge `(i,j)` of `c` and facet `(start,f)`.

Traversal of the Incident Cells, Facets and Edges, and the Adjacent Vertices of a Given Vertex
template<class OutputIterator >
OutputIterator	incident_cells (Vertex_handle v, OutputIterator cells) const
	Copies the `Cell_handle`s of all cells incident to `v` to the output iterator `cells`. More...

bool	try_lock_and_get_incident_cells (Vertex_handle v, std::vector< Cell_handle > &cells) const
	Try to lock and copy the `Cell_handle`s of all cells incident to `v` into `cells`. More...

template<class OutputIterator >
OutputIterator	finite_incident_cells (Vertex_handle v, OutputIterator cells) const
	Copies the `Cell_handle`s of all finite cells incident to `v` to the output iterator `cells`. More...

template<class OutputIterator >
OutputIterator	incident_facets (Vertex_handle v, OutputIterator facets) const
	Copies all `Facet`s incident to `v` to the output iterator `facets`. More...

template<class OutputIterator >
OutputIterator	finite_incident_facets (Vertex_handle v, OutputIterator facets) const
	Copies all finite `Facet`s incident to `v` to the output iterator `facets`. More...

template<class OutputIterator >
OutputIterator	incident_edges (Vertex_handle v, OutputIterator edges) const
	Copies all `Edge`s incident to `v` to the output iterator `edges`. More...

template<class OutputIterator >
OutputIterator	finite_incident_edges (Vertex_handle v, OutputIterator edges) const
	Copies all finite `Edge`s incident to `v` to the output iterator `edges`. More...

template<class OutputIterator >
OutputIterator	adjacent_vertices (Vertex_handle v, OutputIterator vertices) const
	Copies the `Vertex_handle`s of all vertices adjacent to `v` to the output iterator `vertices`. More...

template<class OutputIterator >
OutputIterator	finite_adjacent_vertices (Vertex_handle v, OutputIterator vertices) const
	Copies the `Vertex_handle`s of all finite vertices adjacent to `v` to the output iterator `vertices`. More...

size_type	degree (Vertex_handle v) const
	Returns the degree of a vertex, that is, the number of incident vertices. More...

Traversal Between Adjacent Cells
int	mirror_index (Cell_handle c, int i) const
	Returns the index of `c` in its \( i^{th}\) neighbor. More...

Vertex_handle	mirror_vertex (Cell_handle c, int i) const
	Returns the vertex of the \( i^{th}\) neighbor of `c` that is opposite to `c`. More...

Facet	mirror_facet (Facet f) const
	Returns the same facet seen from the other adjacent cell.

Checking
The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of cells and vertices. We provide the user with the following methods to help debugging.
bool	is_valid (bool verbose=false) const
	This is a function for debugging purpose. More...

bool	is_valid (Cell_handle c, bool verbose=false) const
	This is a function for debugging purpose. More...

I/O
CGAL provides an interface to Geomview for a 3D-triangulation, see Chapter Chapter_Geomview on `Geomview_stream`. #include <CGAL/IO/Triangulation_geomview_ostream_3.h> The information in the `iostream` is: the dimension, the number of finite vertices, the non-combinatorial information about vertices (point, etc; note that the infinite vertex is numbered 0), the number of cells, the indices of the vertices of each cell, plus the non-combinatorial information about each cell, then the indices of the neighbors of each cell, where the index corresponds to the preceding list of cells. When dimension \( <\) 3, the same information is stored for faces of maximal dimension instead of cells.
istream &	operator>> (istream &is, Triangulation_3 &t)
	Reads the underlying combinatorial triangulation from `is` by calling the corresponding input operator of the triangulation data structure class (note that the infinite vertex is numbered 0), and the non-combinatorial information by calling the corresponding input operators of the vertex and the cell classes (such as point coordinates), which are provided by overloading the stream operators of the vertex and cell types. More...

ostream &	operator<< (ostream &os, const Triangulation_3 &t)
	Writes the triangulation `t` into `os`.

Concurrency
void	set_lock_data_structure (Lock_data_structure *lock_ds) const
	Set the pointer to the lock data structure.

Additional Inherited Members
Static Public Member Functions inherited from CGAL::Triangulation_utils_3
static unsigned int	next_around_edge (unsigned int i, unsigned int j)

static int	vertex_triple_index (const int i, const int j)

static unsigned int	ccw (unsigned int i)

static unsigned int	cw (unsigned int i)

Member Enumeration Documentation

◆ Locate_type

template<typename Traits, typename TDS, typename SLDS>

enum CGAL::Triangulation_3::Locate_type

The enum Locate_type is defined by Triangulation_3 to specify which case occurs when locating a point in the triangulation.

Enumerator
VERTEX
EDGE
FACET
CELL
OUTSIDE_CONVEX_HULL
OUTSIDE_AFFINE_HULL

Constructor & Destructor Documentation

◆ Triangulation_3() [1/2]

template<typename Traits, typename TDS, typename SLDS>

CGAL::Triangulation_3< Traits, TDS, SLDS >::Triangulation_3	(	const Geom_traits &	traits = `Geom_traits()`,
		Lock_data_structure *	lock_ds = `nullptr`
	)

Introduces a triangulation t having only one vertex which is the infinite vertex.

lock_ds is an optional pointer to the lock data structure for parallel operations. It must be provided if concurrency is enabled.

◆ Triangulation_3() [2/2]

template<typename Traits, typename TDS, typename SLDS>

CGAL::Triangulation_3< Traits, TDS, SLDS >::Triangulation_3 ( const Triangulation_3< Traits, TDS, SLDS > & tr )

Copy constructor.

All vertices and faces are duplicated. The pointer to the lock data structure is not copied. Thus, the copy won't be concurrency-safe as long as the user has not call Triangulation_3::set_lock_data_structure.

Member Function Documentation

◆ adjacent_vertices()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::adjacent_vertices	(	Vertex_handle	v,
		OutputIterator	vertices
	)		const

Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices.

If t.dimension() < 0, then do nothing. Returns the resulting output iterator.

Precondition: v != Vertex_handle(), t.is_vertex(v).

◆ all_cell_handles()

template<typename Traits, typename TDS, typename SLDS>

All_cell_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::all_cell_handles ( ) const

returns a range of iterators over all cells (even the infinite cells).

Returns an empty range when t.number_of_cells() == 0.

Note: While the value type of All_cells_iterator is Cell, the value type of All_cell_handles::iterator is Cell_handle.

◆ all_cells_begin()

template<typename Traits, typename TDS, typename SLDS>

All_cells_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_cells_begin ( ) const

Starts at an arbitrary cell.

Iterates over all cells (even infinite ones). Returns cells_end() when t.dimension() < 3.

◆ all_edges()

template<typename Traits, typename TDS, typename SLDS>

All_edges CGAL::Triangulation_3< Traits, TDS, SLDS >::all_edges ( ) const

returns a range of iterators starting at an arbitrary edge.

Returns an empty range when t.dimension() < 2.

◆ all_edges_begin()

template<typename Traits, typename TDS, typename SLDS>

All_edges_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_edges_begin ( ) const

Starts at an arbitrary edge.

Iterates over all edges (even infinite ones). Returns edges_end() when t.dimension() < 1.

◆ all_facets()

template<typename Traits, typename TDS, typename SLDS>

All_facets CGAL::Triangulation_3< Traits, TDS, SLDS >::all_facets ( ) const

returns a range of iterators starting at an arbitrary facet.

Returns an empty range when t.dimension() < 2.

◆ all_facets_begin()

template<typename Traits, typename TDS, typename SLDS>

All_facets_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_facets_begin ( ) const

Starts at an arbitrary facet.

Iterates over all facets (even infinite ones). Returns facets_end() when t.dimension() < 2.

◆ all_vertex_handles()

template<typename Traits, typename TDS, typename SLDS>

All_vertex_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::all_vertex_handles ( ) const

returns a range of iterators over all vertices (even the infinite one).

Note: While the value type of All_vertices_iterator is Vertex, the value type of All_vertex_handles::iterator is Vertex_handle.

◆ all_vertices_begin()

template<typename Traits, typename TDS, typename SLDS>

All_vertices_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_vertices_begin ( ) const

Starts at an arbitrary vertex.

Iterates over all vertices (even the infinite one).

◆ are_equal()

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::are_equal	(	const Facet &	f,
		Cell_handle	n,
		int	j
	)		const

For these three methods:

Precondition: t.dimension() == 3.

◆ degree()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::degree ( Vertex_handle v ) const

Returns the degree of a vertex, that is, the number of incident vertices.

The infinite vertex is counted.

Precondition: v != Vertex_handle(), t.is_vertex(v).

◆ finite_adjacent_vertices()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_adjacent_vertices	(	Vertex_handle	v,
		OutputIterator	vertices
	)		const

Copies the Vertex_handles of all finite vertices adjacent to v to the output iterator vertices.

If t.dimension() < 0, then do nothing. Returns the resulting output iterator.

Precondition: v != Vertex_handle(), t.is_vertex(v).

◆ finite_cell_handles()

template<typename Traits, typename TDS, typename SLDS>

Finite_cell_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_cell_handles ( ) const

returns a range of iterators over finite cells.

Returns an empty range when t.number_of_cells() == 0.

Note: While the value type of Finite_cells_iterator is Cell, the value type of Finite_cell_handles::iterator is Cell_handle.

◆ finite_cells_begin()

template<typename Traits, typename TDS, typename SLDS>

Finite_cells_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_cells_begin ( ) const

Starts at an arbitrary finite cell.

Then ++ and -- will iterate over finite cells. Returns finite_cells_end() when t.dimension() < 3.

◆ finite_edges()

template<typename Traits, typename TDS, typename SLDS>

Finite_edges CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_edges ( ) const

returns a range of iterators starting at an arbitrary edge.

Returns an empty range when t.dimension() < 2.

◆ finite_edges_begin()

template<typename Traits, typename TDS, typename SLDS>

Finite_edges_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_edges_begin ( ) const

Starts at an arbitrary finite edge.

Then ++ and -- will iterate over finite edges.

◆ finite_facets()

template<typename Traits, typename TDS, typename SLDS>

Finite_facets CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_facets ( ) const

returns a range of iterators starting at an arbitrary facet.

Returns an empty range when t.dimension() < 2.

◆ finite_facets_begin()

template<typename Traits, typename TDS, typename SLDS>

Finite_facets_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_facets_begin ( ) const

Starts at an arbitrary finite facet.

Then ++ and -- will iterate over finite facets. Returns finite_facets_end() when t.dimension() < 2.

◆ finite_incident_cells()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_cells	(	Vertex_handle	v,
		OutputIterator	cells
	)		const

Copies the Cell_handles of all finite cells incident to v to the output iterator cells.

Returns the resulting output iterator.

Precondition: t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v).

◆ finite_incident_edges()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_edges	(	Vertex_handle	v,
		OutputIterator	edges
	)		const

Copies all finite Edges incident to v to the output iterator edges.

Returns the resulting output iterator.

Precondition: t.dimension() > 0, v != Vertex_handle(), t.is_vertex(v).

◆ finite_incident_facets()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_facets	(	Vertex_handle	v,
		OutputIterator	facets
	)		const

Copies all finite Facets incident to v to the output iterator facets.

Returns the resulting output iterator.

Precondition: t.dimension() > 1, v != Vertex_handle(), t.is_vertex(v).

◆ finite_vertex_handles()

template<typename Traits, typename TDS, typename SLDS>

Finite_vertex_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_vertex_handles ( ) const

returns a range of iterators over finite vertices.

Note: While the value type of Finite_vertices_iterator is Vertex, the value type of Finite_vertex_handles::iterator is Vertex_handle.

◆ finite_vertices_begin()

template<typename Traits, typename TDS, typename SLDS>

Finite_vertices_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_vertices_begin ( ) const

Starts at an arbitrary finite vertex.

Then ++ and -- will iterate over finite vertices.

◆ flip() [1/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::flip	(	Cell_handle	c,
		int	i,
		int	j
	)

Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive).

They return false or true according to this test.

◆ flip() [2/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::flip	(	Cell_handle	c,
		int	i
	)

Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive).

They return false or true according to this test.

◆ flip_flippable() [1/2]

template<typename Traits, typename TDS, typename SLDS>

void CGAL::Triangulation_3< Traits, TDS, SLDS >::flip_flippable	(	Cell_handle	c,
		int	i,
		int	j
	)

Should be preferred to the previous methods when the edge is known to be flippable.

Precondition: The edge is flippable.

◆ flip_flippable() [2/2]

template<typename Traits, typename TDS, typename SLDS>

void CGAL::Triangulation_3< Traits, TDS, SLDS >::flip_flippable	(	Cell_handle	c,
		int	i
	)

Should be preferred to the previous methods when the facet is known to be flippable.

Precondition: The facet is flippable.

◆ has_vertex() [1/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::has_vertex	(	const Facet &	f,
		Vertex_handle	v,
		int &	j
	)		const

If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true.

Precondition: t.dimension() == 3

◆ has_vertex() [2/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::has_vertex	(	Cell_handle	c,
		int	i,
		Vertex_handle	v,
		int &	j
	)		const

Same for facet (c,i).

Computes the index j of v in c.

◆ incident_cells() [1/3]

template<typename Traits, typename TDS, typename SLDS>

Cell_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells ( Edge e ) const

Starts at an arbitrary cell incident to e.

Precondition: t.dimension() == 3.

◆ incident_cells() [2/3]

template<typename Traits, typename TDS, typename SLDS>

Cell_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells	(	Edge	e,
		Cell_handle	start
	)		const

Starts at cell start.

Precondition: t.dimension() == 3 and start is incident to e.

◆ incident_cells() [3/3]

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells	(	Vertex_handle	v,
		OutputIterator	cells
	)		const

Copies the Cell_handles of all cells incident to v to the output iterator cells.

Returns the resulting output iterator.

Precondition: t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v).

◆ incident_edges()

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_edges	(	Vertex_handle	v,
		OutputIterator	edges
	)		const

Copies all Edges incident to v to the output iterator edges.

Returns the resulting output iterator.

Precondition: t.dimension() > 0, v != Vertex_handle(), t.is_vertex(v).

◆ incident_facets() [1/3]

template<typename Traits, typename TDS, typename SLDS>

Facet_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets ( Edge e ) const

Starts at an arbitrary facet incident to e.

Precondition: t.dimension() == 3

◆ incident_facets() [2/3]

template<typename Traits, typename TDS, typename SLDS>

Facet_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets	(	Edge	e,
		Facet	start
	)		const

Starts at facet start.

Precondition: start is incident to e.

◆ incident_facets() [3/3]

template<typename Traits, typename TDS, typename SLDS>

template<class OutputIterator >

OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets	(	Vertex_handle	v,
		OutputIterator	facets
	)		const

Copies all Facets incident to v to the output iterator facets.

Returns the resulting output iterator.

Precondition: t.dimension() > 1, v != Vertex_handle(), t.is_vertex(v).

◆ inexact_locate()

template<typename Traits, typename TDS, typename SLDS>

Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::inexact_locate	(	const Point &	query,
		Cell_handle	start = `Cell_handle()`
	)		const

Same as locate() but uses inexact predicates.

This function returns a handle on a cell that is a good approximation of the exact location of query, while being faster. Note that it may return a handle on a cell whose interior does not contain query. When the triangulation has dimension smaller than 3, start is returned.

Note that this function is available only if the cartesian coordinates of query are accessible with functions x(), y() and z().

◆ insert() [1/3]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert	(	const Point &	p,
		Cell_handle	start = `Cell_handle()`
	)

Inserts the point p in the triangulation and returns the corresponding vertex.

If point p coincides with an already existing vertex, this vertex is returned and the triangulation remains unchanged.

If point p lies in the convex hull of the points, it is added naturally: if it lies inside a cell, the cell is split into four cells, if it lies on a facet, the two incident cells are split into three cells, if it lies on an edge, all the cells incident to this edge are split into two cells.

If point p is strictly outside the convex hull but in the affine hull, p is linked to all visible points on the convex hull to form the new triangulation. See Figure Triangulation3figinsert_outside_convex_hull.

If point p is outside the affine hull of the points, p is linked to all the points, and the dimension of the triangulation is incremented. All the points now belong to the boundary of the convex hull, so, the infinite vertex is linked to all the points to triangulate the new infinite face. See Figure Triangulation3figinsert_outside_affine_hull. The optional argument start is used as a starting place for the search.

◆ insert() [2/3]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert	(	const Point &	p,
		Locate_type	lt,
		Cell_handle	loc,
		int	li,
		int	lj
	)

Inserts the point p in the triangulation and returns the corresponding vertex.

Similar to the above insert() function, but takes as additional parameter the return values of a previous location query. See description of locate() above.

◆ insert() [3/3]

template<typename Traits, typename TDS, typename SLDS>

template<class PointWithInfoInputIterator >

std::ptrdiff_t CGAL::Triangulation_3< Traits, TDS, SLDS >::insert	(	PointWithInfoInputIterator	first,
		PointWithInfoInputIterator	last
	)

Inserts the points in the iterator range [first,last) in the given order, and returns the number of inserted points.

Given a pair (p,i), the vertex v storing p also stores i, that is v.point() == p and v.info() == i. If several pairs have the same point, only one vertex is created, and one of the objects of type Vertex::Info will be stored in the vertex.

Precondition: Vertex must be model of the concept TriangulationVertexBaseWithInfo_3.

Template Parameters

PointWithInfoInputIterator must be an input iterator with the value type std::pair<Point,Vertex::Info>.

◆ insert_in_cell()

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_cell	(	const Point &	p,
		Cell_handle	c
	)

Inserts the point p in the cell c.

The cell c is split into 4 tetrahedra.

Precondition: t.dimension() == 3 and p lies strictly inside cell c.

◆ insert_in_edge() [1/2]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_edge	(	const Point &	p,
		const Edge &	e
	)

Inserts p in the edge e.

In dimension 3, all the cells having this edge are split into 2 tetrahedra; in dimension 2, the 2 neighboring facets are split into 2 triangles; in dimension 1, the edge is split into 2 edges.

Precondition: t.dimension() \( \geq1\) and p lies on edge e.

◆ insert_in_edge() [2/2]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_edge	(	const Point &	p,
		Cell_handle	c,
		int	i,
		int	j
	)

As above, inserts p in the edge \( (i, j)\) of c.

Precondition: As above and \( i\neq j\). Moreover \( i,j \in\{0,1,2,3\}\) in dimension 3, \( i,j \in\{0,1,2\}\) in dimension 2, \( i,j \in\{0,1\}\) in dimension 1.

◆ insert_in_facet() [1/2]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_facet	(	const Point &	p,
		const Facet &	f
	)

Inserts the point p in the facet f.

In dimension 3, the 2 neighboring cells are split into 3 tetrahedra; in dimension 2, the facet is split into 3 triangles.

Precondition: t.dimension() \( \geq2\) and p lies strictly inside face f.

◆ insert_in_facet() [2/2]

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_facet	(	const Point &	p,
		Cell_handle	c,
		int	i
	)

As above, insertion in the facet (c,i).

Precondition: As above and \( i \in\{0,1,2,3\}\) in dimension 3, \( i = 3\) in dimension 2.

◆ insert_in_hole()

template<typename Traits, typename TDS, typename SLDS>

template<class CellIt >

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_hole	(	const Point &	p,
		CellIt	cell_begin,
		CellIt	cell_end,
		Cell_handle	begin,
		int	i
	)

Creates a new vertex by starring a hole.

It takes an iterator range [cell_begin,cell_end) of Cell_handles which specifies a hole: a set of connected cells (resp. facets in dimension 2) which is star-shaped wrt p. (begin, i) is a facet (resp. an edge) on the boundary of the hole, that is, begin belongs to the set of cells (resp. facets) previously described, and begin->neighbor(i) does not. Then this function deletes all the cells (resp. facets) describing the hole, creates a new vertex v, and for each facet (resp. edge) on the boundary of the hole, creates a new cell (resp. facet) with v as vertex. Then v->set_point(p) is called and v is returned.

This operation is equivalent to calling tds().insert_in_hole(cell_begin, cell_end, begin, i); v->set_point(p).

Precondition: t.dimension() \( \geq2\), the set of cells (resp. facets in dimension 2) is connected, its boundary is connected, and p lies inside the hole, which is star-shaped wrt p.

◆ insert_outside_affine_hull()

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_outside_affine_hull ( const Point & p )

p is linked to all the points, and the infinite vertex is linked to all the points (including p) to triangulate the new infinite face, so that all the points now belong to the boundary of the convex hull.

See Figure Triangulation3figinsert_outside_affine_hull.

This method can be used to insert the first point in an empty triangulation.

Precondition: t.dimension() < 3 and p lies outside the affine hull of the points.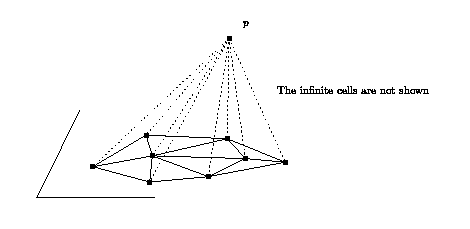

insert_outside_affine_hull() (2-dimensional case)

◆ insert_outside_convex_hull()

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_outside_convex_hull	(	const Point &	p,
		Cell_handle	c
	)

The cell c must be an infinite cell containing p.

Links p to all points in the triangulation that are visible from p. Updates consequently the infinite faces. See Figure Triangulation3figinsert_outside_convex_hull.

Precondition: t.dimension() > 0, c, and the \( k\)-face represented by c is infinite and contains t.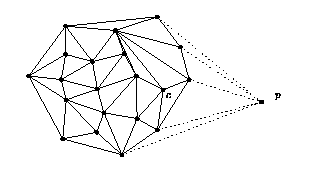

insert_outside_convex_hull() (2-dimensional case)

◆ is_cell() [1/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_cell	(	Vertex_handle	u,
		Vertex_handle	v,
		Vertex_handle	w,
		Vertex_handle	x,
		Cell_handle &	c,
		int &	i,
		int &	j,
		int &	k,
		int &	l
	)		const

Tests whether (u,v,w,x) is a cell of t.

If the cell c is found, the method computes the indices i, j, k and l of the vertices u, v, w and x in c, in this order.

Precondition: u, v, w and x are vertices of t.

◆ is_cell() [2/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_cell	(	Vertex_handle	u,
		Vertex_handle	v,
		Vertex_handle	w,
		Vertex_handle	x,
		Cell_handle &	c
	)		const

Tests whether (u,v,w,x) is a cell of t and computes this cell c.

Precondition: u, v, w and x are vertices of t.

◆ is_edge()

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_edge	(	Vertex_handle	u,
		Vertex_handle	v,
		Cell_handle &	c,
		int &	i,
		int &	j
	)		const

Tests whether (u,v) is an edge of t.

If the edge is found, it gives a cell c having this edge and the indices i and j of the vertices u and v in c, in this order.

Precondition: u and v are vertices of t.

◆ is_facet()

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_facet	(	Vertex_handle	u,
		Vertex_handle	v,
		Vertex_handle	w,
		Cell_handle &	c,
		int &	i,
		int &	j,
		int &	k
	)		const

Tests whether (u,v,w) is a facet of t.

If the facet is found, it computes a cell c having this facet and the indices i, j and k of the vertices u, v and w in c, in this order.

Precondition: u, v and w are vertices of t.

◆ is_infinite() [1/5]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite ( Cell_handle c ) const

true, iff c is incident to the infinite vertex.

Precondition: t.dimension() == 3.

◆ is_infinite() [2/5]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite	(	Cell_handle	c,
		int	i
	)		const

true, iff the facet i of cell c is incident to the infinite vertex.

Precondition: t.dimension() \( \geq2\) and \( i\in\{0,1,2,3\}\) in dimension 3, \( i=3\) in dimension 2.

◆ is_infinite() [3/5]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite ( const Facet & f ) const

true iff facet f is incident to the infinite vertex.

Precondition: t.dimension() \( \geq2\).

◆ is_infinite() [4/5]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite	(	Cell_handle	c,
		int	i,
		int	j
	)		const

true, iff the edge (i,j) of cell c is incident to the infinite vertex.

Precondition: t.dimension() \( \geq1\) and \( i\neq j\). Moreover \( i,j \in\{0,1,2,3\}\) in dimension 3, \( i,j \in\{0,1,2\}\) in dimension 2, \( i,j \in\{0,1\}\) in dimension 1.

◆ is_infinite() [5/5]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite ( const Edge & e ) const

true iff edge e is incident to the infinite vertex.

Precondition: t.dimension() \( \geq1\).

◆ is_valid() [1/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_valid ( bool verbose = false ) const

This is a function for debugging purpose.

Debugging Support

Checks the combinatorial validity of the triangulation. Checks also the validity of its geometric embedding (see Section Representation). When verbose is set to true, messages describing the first invalidity encountered are printed.

◆ is_valid() [2/2]

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_valid	(	Cell_handle	c,
		bool	verbose = `false`
	)		const

This is a function for debugging purpose.

Debugging Support

Checks the combinatorial validity of the cell by calling the is_valid method of the cell class. Also checks the geometric validity of c, if c is finite. (See Section Representation.)

When verbose is set to true, messages are printed to give a precise indication of the kind of invalidity encountered.

◆ is_vertex()

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_vertex	(	const Point &	p,
		Vertex_handle &	v
	)		const

Tests whether p is a vertex of t by locating p in the triangulation.

If p is found, the associated vertex v is given.

◆ locate() [1/2]

template<typename Traits, typename TDS, typename SLDS>

Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::locate	(	const Point &	query,
		Cell_handle	start = `Cell_handle()`,
		bool *	could_lock_zone = `nullptr`
	)		const

If the point query lies inside the convex hull of the points, the cell that contains the query in its interior is returned.

If query lies on a facet, an edge or on a vertex, one of the cells having query on its boundary is returned.

If the point query lies outside the convex hull of the points, an infinite cell with vertices \( \{ p, q, r, \infty\}\) is returned such that the tetrahedron \( ( p, q, r, query )\) is positively oriented (the rest of the triangulation lies on the other side of facet \( ( p, q, r )\)).

Note that locate works even in degenerate dimensions: in dimension 2 (resp. 1, 0) the Cell_handle returned is the one that represents the facet (resp. edge, vertex) containing the query point.

The optional argument start is used as a starting place for the search.

The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. When the pointer is not null, the locate will try to lock all the cells along the walk. If it succeeds, *could_lock_zone is true, otherwise it is false. In any case, the locked cells are not unlocked by locate, leaving this choice to the user.

◆ locate() [2/2]

template<typename Traits, typename TDS, typename SLDS>

Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::locate	(	const Point &	query,
		Locate_type &	lt,
		int &	li,
		int &	lj,
		Cell_handle	start = `Cell_handle()`,
		bool *	could_lock_zone = `nullptr`
	)		const

If query lies inside the affine hull of the points, the \( k\)-face (finite or infinite) that contains query in its interior is returned, by means of the cell returned together with lt, which is set to the locate type of the query (VERTEX, EDGE, FACET, CELL, or OUTSIDE_CONVEX_HULL if the cell is infinite and query lies strictly in it) and two indices li and lj that specify the \( k\)-face of the cell containing query.

If the \( k\)-face is a cell, li and lj have no meaning; if it is a facet (resp. vertex), li gives the index of the facet (resp. vertex) and lj has no meaning; if it is and edge, li and lj give the indices of its vertices.

If the point query lies outside the affine hull of the points, which can happen in case of degenerate dimensions, lt is set to OUTSIDE_AFFINE_HULL, and the cell returned has no meaning. As a particular case, if there is no finite vertex yet in the triangulation, lt is set to OUTSIDE_AFFINE_HULL and locate returns the default constructed handle.

The optional argument start is used as a starting place for the search.

The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. When the pointer is not null, the locate will try to lock all the cells along the walk. If it succeeds, *could_lock_zone is true, otherwise it is false. In any case, the locked cells are not unlocked by locate, leaving this choice to the user.

◆ mirror_index()

template<typename Traits, typename TDS, typename SLDS>

int CGAL::Triangulation_3< Traits, TDS, SLDS >::mirror_index	(	Cell_handle	c,
		int	i
	)		const

Returns the index of c in its \( i^{th}\) neighbor.

Precondition: \( i \in\{0, 1, 2, 3\}\).

◆ mirror_vertex()

template<typename Traits, typename TDS, typename SLDS>

Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::mirror_vertex	(	Cell_handle	c,
		int	i
	)		const

Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c.

Precondition: \( i \in\{0, 1, 2, 3\}\).

◆ number_of_edges()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_edges ( ) const

The number of edges.

Returns 0 if t.dimension() < 1.

◆ number_of_facets()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_facets ( ) const

The number of facets.

Returns 0 if t.dimension() < 2.

◆ number_of_finite_cells()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_cells ( ) const

The number of finite cells.

Returns 0 if t.dimension() < 3.

◆ number_of_finite_edges()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_edges ( ) const

The number of finite edges.

Returns 0 if t.dimension() < 1.

◆ number_of_finite_facets()

template<typename Traits, typename TDS, typename SLDS>

size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_facets ( ) const

The number of finite facets.

Returns 0 if t.dimension() < 2.

◆ operator=()

template<typename Traits, typename TDS, typename SLDS>

Triangulation_3& CGAL::Triangulation_3< Traits, TDS, SLDS >::operator= ( const Triangulation_3< Traits, TDS, SLDS > & tr )

The triangulation tr is duplicated, and modifying the copy after the duplication does not modify the original.

The previous triangulation held by t is deleted.

◆ operator==()

template<typename Traits, typename TDS, typename SLDS>

template<class GT , class Tds1 , class Tds2 >

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::operator==	(	const Triangulation_3< GT, Tds1 > &	t1,
		const Triangulation_3< GT, Tds2 > &	t2
	)

Equality operator.

Returns true iff there exist a bijection between the vertices of t1 and those of t2 and a bijection between the cells of t1 and those of t2, which preserve the geometry of the triangulation, that is, the points of each corresponding pair of vertices are equal, and the tetrahedra corresponding to each pair of cells are equal (up to a permutation of their vertices).

◆ operator>>()

template<typename Traits, typename TDS, typename SLDS>

istream& CGAL::Triangulation_3< Traits, TDS, SLDS >::operator>>	(	istream &	is,
		Triangulation_3< Traits, TDS, SLDS > &	t
	)

Reads the underlying combinatorial triangulation from is by calling the corresponding input operator of the triangulation data structure class (note that the infinite vertex is numbered 0), and the non-combinatorial information by calling the corresponding input operators of the vertex and the cell classes (such as point coordinates), which are provided by overloading the stream operators of the vertex and cell types.

Assigns the resulting triangulation to t.

◆ point() [1/2]

template<typename Traits, typename TDS, typename SLDS>

const Point& CGAL::Triangulation_3< Traits, TDS, SLDS >::point	(	Cell_handle	c,
		int	i
	)		const

Returns the point given by vertex i of cell c.

Precondition: t.dimension() \( \geq0\) and \( i \in\{0,1,2,3\}\) in dimension 3, \( i \in\{0,1,2\}\) in dimension 2, \( i \in\{0,1\}\) in dimension 1, \( i = 0\) in dimension 0, and the vertex is finite.

Examples:: Triangulation_3/for_loop.cpp.

◆ point() [2/2]

template<typename Traits, typename TDS, typename SLDS>

const Point& CGAL::Triangulation_3< Traits, TDS, SLDS >::point ( Vertex_handle v ) const

Same as the previous method for vertex v.

Precondition: t.dimension() \( \geq0\) and the vertex is finite.

◆ segment() [1/2]

template<typename Traits, typename TDS, typename SLDS>

Segment CGAL::Triangulation_3< Traits, TDS, SLDS >::segment ( const Edge & e ) const

Returns the line segment formed by the vertices of e.

Precondition: t.dimension() \( \geq1\) and e is finite.

◆ segment() [2/2]

template<typename Traits, typename TDS, typename SLDS>

Segment CGAL::Triangulation_3< Traits, TDS, SLDS >::segment	(	Cell_handle	c,
		int	i,
		int	j
	)		const

Same as the previous method for edge (c,i,j).

Precondition: As above and \( i\neq j\). Moreover \( i,j \in\{0,1,2,3\}\) in dimension 3, \( i,j \in\{0,1,2\}\) in dimension 2, \( i,j \in\{0,1\}\) in dimension 1, and the edge is finite.

◆ set_infinite_vertex()

template<typename Traits, typename TDS, typename SLDS>

void CGAL::Triangulation_3< Traits, TDS, SLDS >::set_infinite_vertex ( Vertex_handle v )

This is an advanced function.

Advanced

This method is meant to be used only if you have done a low-level operation on the underlying tds that invalidated the infinite vertex. Sets the infinite vertex.

◆ side_of_cell()

template<typename Traits, typename TDS, typename SLDS>

Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_cell	(	const Point &	p,
		Cell_handle	c,
		Locate_type &	lt,
		int &	li,
		int &	lj
	)		const

Returns a value indicating on which side of the oriented boundary of c the point p lies.

More precisely, it returns:

ON_BOUNDED_SIDE if p is inside the cell. For an infinite cell this means that p lies strictly in the half space limited by its finite facet and not containing any other point of the triangulation.
ON_BOUNDARY if p on the boundary of the cell. For an infinite cell this means that p lies on the finite facet. Then lt together with li and lj give the precise location on the boundary. (See the descriptions of the locate methods.)
ON_UNBOUNDED_SIDE if p lies outside the cell. For an infinite cell this means that p does not satisfy either of the two previous conditions.
Precondition
t.dimension() == 3

◆ side_of_edge()

template<typename Traits, typename TDS, typename SLDS>

Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_edge	(	const Point &	p,
		const Edge &	e,
		Locate_type &	lt,
		int &	li
	)		const

Returns a value indicating on which side of the oriented boundary of e the point p lies:

ON_BOUNDED_SIDE if p is inside the edge. For an infinite edge this means that p lies in the half line defined by the vertex and not containing any other point of the triangulation.
ON_BOUNDARY if p equals one of the vertices, li give the index of the vertex in the cell storing e
ON_UNBOUNDED_SIDE if p lies outside the edge. For an infinite edge this means that p lies on the other half line, which contains the other points of the triangulation.
Precondition
t.dimension() == 1 and p is collinear with the points of the triangulation. e.second == 0 and e.third \( =1\) (in dimension 1 there is only one edge per cell).

◆ side_of_facet()

template<typename Traits, typename TDS, typename SLDS>

Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_facet	(	const Point &	p,
		const Facet &	f,
		Locate_type &	lt,
		int &	li,
		int &	lj
	)		const

Returns a value indicating on which side of the oriented boundary of f the point p lies:

ON_BOUNDED_SIDE if p is inside the facet. For an infinite facet this means that p lies strictly in the half plane limited by its finite edge and not containing any other point of the triangulation .
ON_BOUNDARY if p is on the boundary of the facet. For an infinite facet this means that p lies on the finite edge. lt, li and lj give the precise location of p on the boundary of the facet. li and lj refer to indices in the degenerate cell c representing f.
ON_UNBOUNDED_SIDE if p lies outside the facet. For an infinite facet this means that p does not satisfy either of the two previous conditions.

Precondition: t.dimension() == 2 and p lies in the plane containing the triangulation. f.second \( =3\) (in dimension 2 there is only one facet per cell).

◆ swap()

template<typename Traits, typename TDS, typename SLDS>

void CGAL::Triangulation_3< Traits, TDS, SLDS >::swap ( Triangulation_3< Traits, TDS, SLDS > & tr )

The triangulations tr and t are swapped.

t.swap(tr) should be preferred to t = tr or to t(tr) if tr is deleted after that. Indeed, there is no copy of cells and vertices, thus this method runs in constant time.

◆ tds()

template<typename Traits, typename TDS, typename SLDS>

Triangulation_data_structure& CGAL::Triangulation_3< Traits, TDS, SLDS >::tds ( )

Returns a reference to the triangulation data structure.

Advanced

This method is mainly a help for users implementing their own triangulation algorithms. The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of the tds.

◆ tetrahedron()

template<typename Traits, typename TDS, typename SLDS>

Tetrahedron CGAL::Triangulation_3< Traits, TDS, SLDS >::tetrahedron ( Cell_handle c ) const

Returns the tetrahedron formed by the four vertices of c.

Precondition: t.dimension() == 3 and the cell is finite.

◆ triangle() [1/2]

template<typename Traits, typename TDS, typename SLDS>

Triangle CGAL::Triangulation_3< Traits, TDS, SLDS >::triangle	(	Cell_handle	c,
		int	i
	)		const

Returns the triangle formed by the three vertices of facet (c,i).

The triangle is oriented so that its normal points to the inside of cell c.

Precondition: t.dimension() \( \geq2\) and \( i \in\{0,1,2,3\}\) in dimension 3, \( i = 3\) in dimension 2, and the facet is finite.

◆ triangle() [2/2]

template<typename Traits, typename TDS, typename SLDS>

Triangle CGAL::Triangulation_3< Traits, TDS, SLDS >::triangle ( const Facet & f ) const

Same as the previous method for facet f.

Precondition: t.dimension() \( \geq2\) and the facet is finite.

◆ try_lock_and_get_incident_cells()

template<typename Traits, typename TDS, typename SLDS>

bool CGAL::Triangulation_3< Traits, TDS, SLDS >::try_lock_and_get_incident_cells	(	Vertex_handle	v,
		std::vector< Cell_handle > &	cells
	)		const

Try to lock and copy the Cell_handles of all cells incident to v into cells.

Returns true in case of success. Otherwise, cells is emptied and the function returns false. In any case, the locked cells are not unlocked by try_lock_and_get_incident_cells(), leaving this choice to the user.

Precondition: t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v).

Inherits from

Definition

Public Types

Types

Creation

Assignment

Access Functions

Non-Constant-Time Access Functions

Geometric Access Functions

Tests for Finite and Infinite Vertices and Faces

Queries

Point Location

Flips

Insertions

Cell, Face, Edge and Vertex Iterators

Ranges

Cell and Facet Circulators

Traversal of the Incident Cells, Facets and Edges, and the Adjacent Vertices of a Given Vertex

Traversal Between Adjacent Cells

Checking

I/O

Concurrency

Additional Inherited Members

Member Enumeration Documentation

◆ Locate_type

Constructor & Destructor Documentation

◆ Triangulation_3() [1/2]

◆ Triangulation_3() [2/2]

Member Function Documentation

◆ adjacent_vertices()

◆ all_cell_handles()

◆ all_cells_begin()

◆ all_edges()

◆ all_edges_begin()

◆ all_facets()

◆ all_facets_begin()

◆ all_vertex_handles()

◆ all_vertices_begin()

◆ are_equal()

◆ degree()

◆ finite_adjacent_vertices()

◆ finite_cell_handles()

◆ finite_cells_begin()

◆ finite_edges()

◆ finite_edges_begin()

◆ finite_facets()

◆ finite_facets_begin()

◆ finite_incident_cells()

◆ finite_incident_edges()

◆ finite_incident_facets()

◆ finite_vertex_handles()

◆ finite_vertices_begin()

◆ flip() [1/2]

◆ flip() [2/2]

◆ flip_flippable() [1/2]

◆ flip_flippable() [2/2]

◆ has_vertex() [1/2]

◆ has_vertex() [2/2]

◆ incident_cells() [1/3]

◆ incident_cells() [2/3]

◆ incident_cells() [3/3]

◆ incident_edges()

◆ incident_facets() [1/3]

◆ incident_facets() [2/3]

◆ incident_facets() [3/3]

◆ inexact_locate()

◆ insert() [1/3]

◆ insert() [2/3]

◆ insert() [3/3]

◆ insert_in_cell()

◆ insert_in_edge() [1/2]

◆ insert_in_edge() [2/2]

◆ insert_in_facet() [1/2]

◆ insert_in_facet() [2/2]

◆ insert_in_hole()

◆ insert_outside_affine_hull()

◆ insert_outside_convex_hull()

◆ is_cell() [1/2]

◆ is_cell() [2/2]

◆ is_edge()