|
CGAL 5.1.2 - 2D Snap Rounding
|
|
CGAL 5.1.2 - 2D Snap Rounding
|
Snap Rounding (SR, for short) is a well known method for converting arbitrary-precision arrangements of segments into a fixed-precision representation [1], [2], [4]. In the study of robust geometric computing, it can be classified as a finite precision approximation technique. Iterated Snap Rounding (ISR, for short) is a modification of SR in which each vertex is at least half-the-width-of-a-pixel away from any non-incident edge [3]. This package supports both methods. Algorithmic details and experimental results are given in [3].
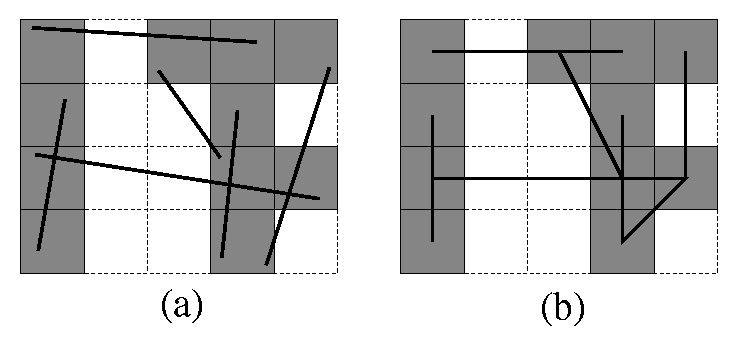
Given a finite collection \( \S\) of segments in the plane, the arrangement of \( \S\) denoted \( \A(\S)\) is the subdivision of the plane into vertices, edges, and faces induced by \( \S\). A vertex of the arrangement is either a segment endpoint or the intersection of two segments. Given an arrangement of segments whose vertices are represented with arbitrary-precision coordinates, the function snap_rounding_2() proceeds as follows. We tile the plane with a grid of unit squares, pixels, each centered at a point with integer coordinates. A pixel is hot if it contains a vertex of the arrangement. Each vertex of the arrangement is replaced by the center of the hot pixel containing it and each edge \( e\) is replaced by the polygonal chain through the centers of the hot pixels met by \( e\), in the same order as they are met by \( e\). Figure 36.1 demonstrates the results of SR.
In a snap-rounded arrangement, the distance between a vertex and a non-incident edge can be extremely small compared with the width of a pixel in the grid used for rounding. ISR is a modification of SR which makes a vertex and a non-incident edge well separated (the distance between each is at least half-the-width-of-a-pixel). However, the guaranteed quality of the approximation in ISR degrades. Figure 36.2 depicts the results of SR and ISR on the same input. Conceptually, the ISR procedure is equivalent to repeated application of SR, namely we apply SR to the original set of segments, then we use the output of SR as input to another round of SR and so on until all the vertices are well separated from non-incident edges. Algorithmically we operate differently, as this repeated application of SR would have resulted in an efficient overall process. The algorithmic details are given in [3].
Our package supports both schemes, implementing the algorithm described in [3]. Although the paper only describes an algorithm for ISR, it is easy to derive an algorithm for SR, by performing only the first rounding level for each segment.
The input to the program is a set \( S\) of \( n\) segments, \( S=\{s_1,\ldots,s_n\}\) and the output is a set \( G\) of \( n\) polylines, with a polyline \( g_i\) for each input segments \( s_i\). An input segment is given by the coordinates of its endpoints. An output polyline is given by the ordered set of vertices \( v_0,\ldots,v_k\) along the polyline. The polyline consists of the segments \( (v_0v_1),\ldots,(v_{k-1}v_k)\).
There are three template parameters: Traits is the underlying geometry, i.e., the number type used and the coordinate representation. InputIterator is the type of the iterators that point to the first and after-the-last elements of the input. Finally, OutputContainer is the type of the output container.
Since the algorithm requires kernel functionalities such as the rounding to the center of a pixel, a special traits class must be provided. The precise description of the requirements is given by the concept SnapRoundingTraits_2. The class Snap_rounding_traits_2 is a model of this concept.
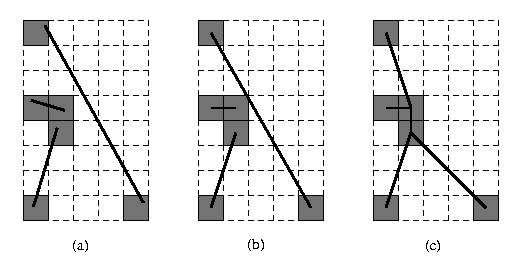
The following example generates an ISR representation of an arrangement of four line segments. In particular it produces a list of points that are the vertices of the resulting polylines in a plane tiled with one-unit square pixels.
File Snap_rounding_2/snap_rounding.cpp
This program generates four polylines, one for each input segment. The exact output follows:
Polyline number 1: (0/4:0/4) (12/4:12/4) (20/4:20/4) (28/4:28/4) (40/4:40/4) Polyline number 2: (0/4:40/4) (12/4:28/4) (20/4:20/4) (28/4:12/4) (40/4:0/4) Polyline number 3: (12/4:0/4) (12/4:12/4) (12/4:28/4) (12/4:40/4) Polyline number 4: (28/4:0/4) (28/4:12/4) (28/4:28/4) (28/4:40/4)
The package is supplied with a graphical demo program that opens a window, allows the user to edit segments dynamically, applies a selected snap-rounding procedures, and displays the result onto the same window (see <CGAL_ROOT>/demo/Snap_rounding_2/demo.cpp).