|
CGAL 5.1.3 - 2D Periodic Hyperbolic Triangulations
|
|
CGAL 5.1.3 - 2D Periodic Hyperbolic Triangulations
|
This package enables the computation of Delaunay triangulations of the Bolza surface, which is the most symmetric surface of genus 2. The Bolza surface is a hyperbolic closed compact orientable surface.
A triangulation of the Bolza surface can be seen as a periodic triangulation of the hyperbolic plane.
Let \(\mathbb{H}^2\) denote the hyperbolic plane, represented in the Poincaré disk model (see Chapter 2D Hyperbolic Delaunay Triangulations). The Bolza surface \(\mathcal{M}\) is defined as the quotient of \(\mathbb H^2\) under the action of a group \(\mathcal G\) that we will introduce now.
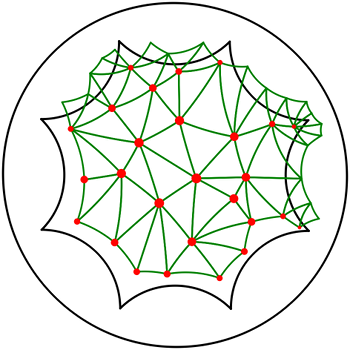
Consider the regular hyperbolic octagon \( \mathcal D_O \) centered at the origin with all angles equal to \( \pi/4\), as shown in Figure 43.1. Note that \(\mathcal D_O\) is unique up to rotation and cannot be scaled since this operation would change its angles. Consider the four hyperbolic translations \( a,b,c,d\) with their respective inverses \(\overline{a}, \overline{b}, \overline{c}, \overline{d}\) that identify the opposite sides of \( \mathcal D_O \). The axes of these translations, shown in Figure 43.1 - Left, are diameters of the Poincaré disk. The four translations \(a, b, c, d\) generate a (non-commutative) discrete group of orientation-preserving isometries, with finite presentation
\[ \mathcal{G} = \left< a,b,c,d \; \bigg| \; abcd\overline{a}\overline{b}\overline{c}\overline{d} \right>. \]
Note that equivalent translations of the group \(\mathcal G\) can be reduced to a unique minimal representative.
The group \(\mathcal G\) is acting on \(\mathbb H^2\): two points \(p\) and \(q\) in \(\mathbb H^2\) are in the same orbit under the action of \(\mathcal G\) if there exists an element \(g \in \mathcal G\) such that \(g(p) = q\), as shown in Figure 43.1 - Center. The Bolza surface \(\mathcal{M}\) is defined as the quotient of \(\mathbb H^2\) under the action of \(\mathcal G\), named the fundamental group of \(\mathcal M\):
\[ \mathcal{M} = \mathbb H^2 / \mathcal{G}. \]
The natural projection map from \(\mathbb H^2\) onto \(\mathcal M\) is denoted with \(\pi\). By definition, all points of \(\mathbb H^2\) that belong to the same orbit under the action of \(\mathcal G\) project by \(\pi\) onto the same point of the surface \(\mathcal M\).
The half-open octagon \(\mathcal D\) shown in Figure 43.1 - Right contains exactly one representative of each point of \(\mathcal{M}\); \(\mathcal D\) is called the original domain of \(\mathcal{M}\). A point outside \(\mathcal D\) is the image of a point in \(\mathcal D\), its representative, under the action of a uniquely defined translation in the group \(\mathcal{G}\).
Figure 43.2 illustrates how a genus-2 surface can be obtained by identifying opposite sides of \(\mathcal D\) under the action of \(\mathcal G\).
In the following, and when there is no risk of confusion, the same notation will be used for a point on the surface \(\mathcal M\) and its representative in \(\mathcal D\). Similarly, \(\mathcal{P}\) will denote both a set of points on the surface and the set of their representatives in \(\mathcal D\).
We require that all input points lie inside \(\mathcal D\).
The Delaunay triangulation of \(\mathcal{M}\) defined by a point set \(\mathcal{P}\) is the projection by \(\pi\) of the Delaunay triangulation in the plane \(\mathbb H^2\) of the (infinite) set of points \(\mathcal{G P}\) onto \(\mathcal{M}\), provided that some condition (detailed in Section Simplicial Embedding Condition below) holds. More details can be found in [1].
As for orbits of points, all faces of the Delaunay triangulation of \(\mathcal{G P}\) that are in the same orbit under the action of \(\mathcal{G}\) project by \(\pi\) onto the same face on the surface \(\mathcal{M}\). We can define a unique canonical representative for each orbit, which has at least one vertex in \(\mathcal D\). Some canonical faces have vertices both inside and outside \(\mathcal D\); such faces can be uniquely specified by three pairs of points in \(\mathcal D\) and reduced translations of \(\mathcal{G}\) (points in the original domain are paired with the identity translation \(\mathbb 1)\). The underlying combinatorial triangulation is a 2D Triangulation Data Structure enriched in each face by the three translations that are paired with the point in each vertex of the canonical representative (see Figure 43.3).
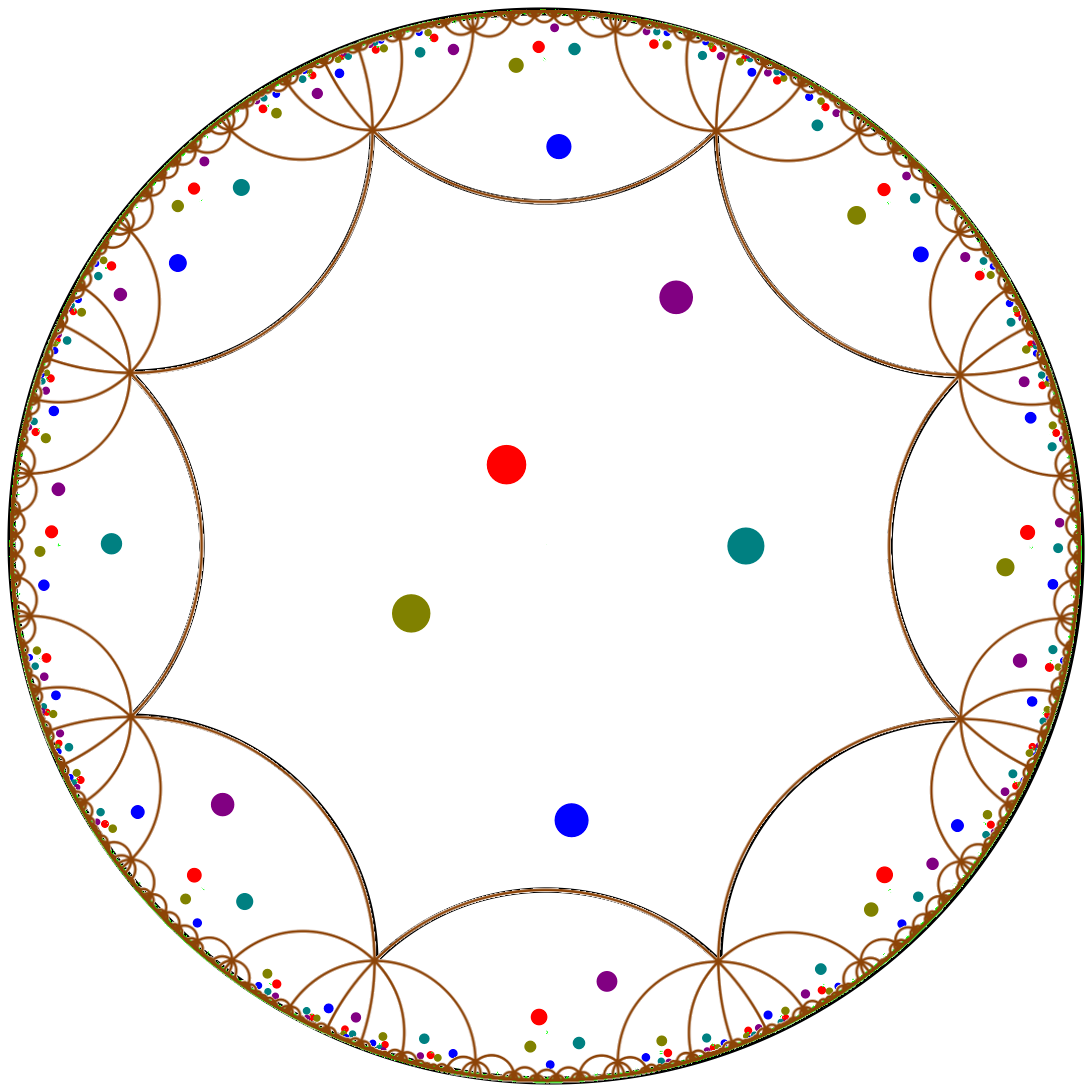
More precisely, the translations are elements of the subset \(\mathcal N\) of \(\mathcal G\) for which the image of \(\mathcal D_O\) has at least one vertex in common with \(\mathcal D_O\). These images of \(\mathcal D_O\) by translations in \(\mathcal N\) are shaded in Figure 43.4; we consider them to be ordered counterclockwise around \(\mathcal D_O\), arbitrarily starting with the one corresponding to translation \(abcd\). The canonical representative in \(\mathbb H^2\) of a face on \(\mathcal M\) is such that
Let us now give details on the condition mentioned above. The projection by \(\pi\) of the Delaunay triangulation in \(\mathbb H^2\) of \(\mathcal{G P}\) is a triangulation of \(\mathcal{M}\) if and only if its combinatorial graph does not contain loops (i.e., edges having two identical vertices) or double edges (i.e., two edges sharing the same two vertices), or, equivalently, if the projection is a simplicial complex:
Some point sets do not define a triangulation of \(\mathcal M\). For instance, a single point does not define a triangulation of \(\mathcal M\), as all edges of the induced subdivision would be loops. Another example is shown in Figure 43.5.
We initialize a triangulation of \(\mathcal M\) with a predetermined set \(\mathcal Q\) of 14 points, called dummy points (see Figure 43.6), which ensures that the projection by \(\pi\) of the Delaunay triangulation of \(\mathcal{G} (\mathcal{P}\cup\mathcal{Q})\) onto \(\mathcal M\) is a simplicial complex for any set of input points \(\mathcal{P}\) [1].
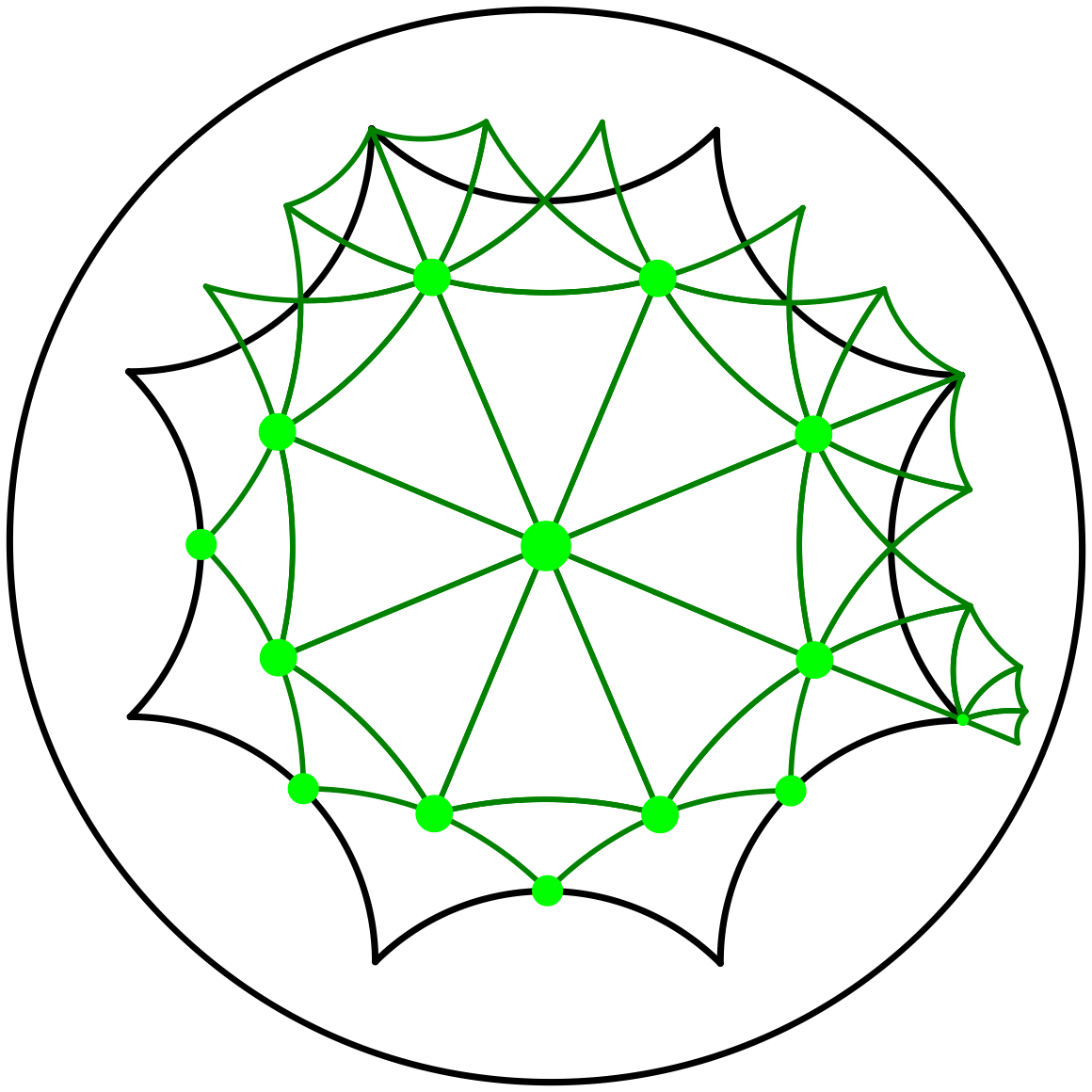
If sufficiently many well-distributed points are inserted, the dummy points become unnecessary, i.e., the subdivision remains a simplicial complex even if we remove them. Otherwise some dummy points are left to ensure that the final subdivision is a simplicial complex.
The main class of this package is Periodic_4_hyperbolic_Delaunay_triangulation_2, which implements Delaunay triangulations of the Bolza surface \(\mathcal M\). The prefix "Periodic_4" emphasizes that the triangulation in the universal covering \(\mathbb H^2\) is periodic in the four directions defined by the hyperbolic translations \( a,b,c\), and \(d\).
The implementation is fully dynamic, supporting both point insertion and vertex removal. However, a vertex can be removed only if the subdivision remains a simplicial complex.
The class Periodic_4_hyperbolic_Delaunay_triangulation_2 provides high-level geometric functionality specific to Delaunay triangulations, such as point insertion and vertex removal, the side-of-circle test, finding the conflicting region of a given point, and dual functions. It inherits from a base class, Periodic_4_hyperbolic_triangulation_2, which provides functionality common to triangulations in general, such as point location [2], and access functions, but supports neither point insertion nor vertex removal.
Both classes Periodic_4_hyperbolic_triangulation_2 and Periodic_4_hyperbolic_Delaunay_triangulation_2 have two template parameters that reflect the separation between the geometric and combinatorial structures of the triangulation:
The geometric traits class must fulfill the requirements described in the concept Periodic_4HyperbolicDelaunayTriangulationTraits_2. Moreover, the traits class must represent hyperbolic translations of the group \(\mathcal G\) via the class Hyperbolic_octagon_translation.
A model for the concept Periodic_4HyperbolicDelaunayTriangulationTraits_2 offered by this package is the class Periodic_4_hyperbolic_Delaunay_triangulation_traits_2. The class has one template parameter:
Kernel with a field number type FT that guarantees exact computations on algebraic numbers with nested square roots. The default value for this parameter is CGAL::Exact_predicates_exact_constructions_kernel_with_sqrt. The triangulation data structure is a container for the faces and vertices and maintains incidence and adjacency relations. This parameter must meet the requirements described in the concept TriangulationDataStructure_2, for which CGAL offers the model Triangulation_data_structure_2. This model is itself parameterized by a vertex base class and a face base class, which gives the possibility to customize the vertices and faces used by the triangulation data structure. To represent periodic hyperbolic triangulations, the face base and vertex base classes must be models of the concepts Periodic_4HyperbolicTriangulationFaceBase_2 and Periodic_4HyperbolicTriangulationVertexBase_2, respectively.
The default value for the triangulation data structure parameter is Triangulation_data_structure_2< Periodic_4_hyperbolic_triangulation_vertex_base_2<Traits>, Periodic_4_hyperbolic_triangulation_face_base_2<Traits> >, where Traits is a model of Periodic_4HyperbolicDelaunayTriangulationTraits_2.
Most functionalities of periodic hyperbolic triangulations are similar to those of Euclidean 2D triangulations. We refer the reader to the following two examples of the 2D Triangulation package:
The example below shows the initialization of a periodic hyperbolic 2D Delaunay triangulation, the insertion of random points uniformly distributed in the unit disk for the Euclidean metric, and the properties of the triangulation after the insertion. It uses the default triangulation data structure.
File Periodic_4_hyperbolic_triangulation_2/p4ht2_example_insertion.cpp
We have measured the insertion execution time of our implementation against other CGAL triangulations. Random points, uniformly distributed in the unit disk with respect to the Euclidean metric, are generated. From these generated points, we select 1 million points that lie in the original octagon \(\mathcal D_O\). We insert the same set of points in three triangulations:
CORE::Expr as number type; CORE::Expr as number type; double as number type. We report results averaged over 10 executions of this experiment in Table 1 below. The experiments have been executed on two machines:
| Triangulation type | Machine 1 | Machine 2 |
|---|---|---|
Periodic hyperbolic (CORE::Expr) | 55 sec. | 40 sec. |
Non-periodic Euclidean (CORE::Expr) | 24 sec. | 20 sec. |
Non-periodic Euclidean (double) | 1 sec. | 1 sec. |
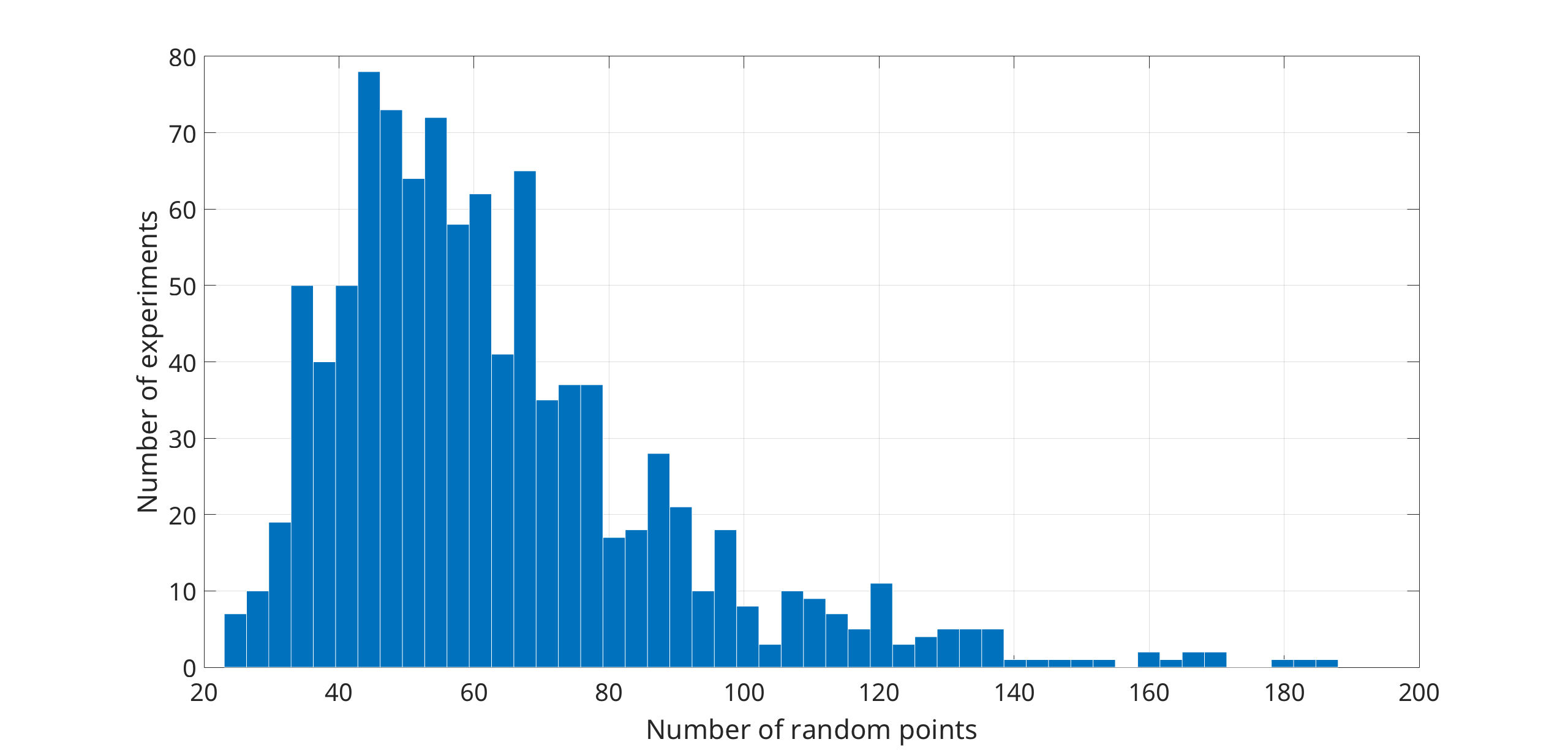
Another experiment shows that, on average, all dummy points are removed from the triangulation with the insertion of fewer than 200 random points uniformly distributed in the unit disk with respect to the Euclidean metric. We start with an empty triangulation of the Bolza surface (i.e., initialized with only the dummy points), and we insert random points one by one. After each insertion, the unnecessary dummy points (if any) are removed from the triangulation. As soon as the last dummy point has been removed, we stop the process and record the number of random points inserted. Results are shown in Figure 43.7.
This package implements the algorithm for the computation of Delaunay triangulation of the Bolza surface proposed by Mikhail Bogdanov, Monique Teillaud, and Gert Vegter [1]. The implementation itself is described by Iordan Iordanov and Monique Teillaud [3].
In 2016, Iordanov started working on the 2D Periodic Hyperbolic Triangulations package.
The authors would like to thank their partners from the Astonishing and SoS projects for very helpful discussions.