|
CGAL 5.1.5 - CGAL and the Boost Graph Library
|
|
CGAL 5.1.5 - CGAL and the Boost Graph Library
|
Many geometric data structures can be interpreted as graphs as they consist of vertices and edges. This is the case for the halfedge data structure, for the polyhedral surface, for the arrangement, and for the 2D triangulation classes. With means of duality one can also interpret faces as vertices and edges between adjacent faces as edges of the dual graph.
The scope of CGAL is geometry and not graph algorithms. Nevertheless, this package provides the necessary classes and functions that enable using the algorithms of the Boost Graph Library [4] (Bgl for short) with CGAL data structures.
Furthermore, this package extends the Bgl by introducing concepts such as HalfedgeGraph and FaceGraph allowing to handle halfedges and faces. These concepts reflect the design of the halfedge data structure described in Chapter Halfedge Data Structures, with opposite halfedges and circular sequences of halfedges around vertices and around faces.
This chapter is organized as follows:
The algorithms of the Bgl operate on models of various graph concepts. The traits class boost::graph_traits enable algorithms to determine the types of vertices and edges (similar to std::iterator_traits for iterators). Free functions that operate on graphs enable algorithms to obtain, for example, the source vertex of an edge, or all edges incident to a vertex. The algorithms use property maps to associate information with vertices and edges. The algorithms enable visitors to register callbacks that are called later on during the execution of the algorithms. Finally, the graph algorithms use the named parameter mechanism, which enables passing the arguments in arbitrary order.
The Bgl introduces several graph concepts, which have different sets of characteristics and requirements. For example, iterating through all vertices or all edges in a graph, obtaining the outgoing or in-going edges of a vertex, inserting vertices and edges into a graph, and removing vertices and edges from a graph.
An algorithm operating on a graph model determines types with the help of the traits class boost::graph_traits. Such types are the vertex_descriptor, which is similar to a vertex handle in CGAL data structures, or the edge_descriptor, which is similar to the halfedge handle in the halfedge data structure or to the type Edge in 2D triangulations. There are also iterators, such as the vertex_iterator, which is similar to a vertex iterator in CGAL data structures, and the out_edge_iterator, which is similar to the edge circulator; it enables to iterate through the edges incident to a vertex. The iterators are similar and not equivalent, because their value type is a vertex_descriptor, whereas in CGAL handles, iterators, and circulators all have the same value type, namely the vertex or edge types.
Given a graph type G, definitions of descriptors and iterators look as follows:
Algorithms obtain incidence information in graphs with the help of global functions such as:
std::pair<vertex_iterator,vertex_iterator> vertices(const Graph& g); to obtain an iterator range providing access to all the vertices, orint num_vertices(const Graph&); to obtain the number of vertices of a graph, orvertex_descriptor source(edge_descriptor, const Graph&); to obtain the source vertex of an edge.Note, that the way we have written the types is a simplification; in reality, the signature of the first of the above functions is:
Another feature extensively used in the Bgl is the property map, which is offered by the Boost Property Map Library. Property maps are a general purpose interface for mapping key objects to corresponding value objects.
The Bgl uses property maps to associate information with vertices and edges. This mechanism uses a traits class (boost::property_traits) and free functions to read (get) and write (put) information in vertices, edges, and also in halfedges and faces for models of the CGAL graph concepts. For example, the Bgl Dijksta's shortest path algorithm writes the predecessor of each vertex, as well as the distance to the source in such a property map.
Some default property maps are associated with the graph types. They are called internal property maps and can be retrieved using an overload of the function get(). For example,
returns a property map that associates an index in the range [0, num_vertices(g)) with each vertex of the graph. This reduces the number of parameters to pass. The data itself may be stored in the vertex or the edge, or it may be stored in an external data structure, or it may be computed on the fly. This is an implementation detail of a particular property map.
See also Chapter CGAL and Boost Property Maps.
Visitors are objects that provide functions to be called at specified event points by the algorithm that they visit. The functions as well as the event points are algorithm-specific. Examples of such event points in graph algorithms are when a vertex is traversed the first time, or when all outgoing edges of a vertex have been traversed.
See also Section Visitor Concepts in the Bgl manual.
The notion of named parameters was introduced in the Bgl, and allow the user to specify only those parameters which are really needed, by name, making the parameter ordering unimportant. See also this page in the manual of the Bgl for more information.
Say there is a function f() that takes 3 parameters called name, age and gender, and you have variables n, a and g to pass as parameters to that function. Without named parameters, you would call it like this: f(n,a,g), whereas with named parameters, you call it like this: f(name(n).age(a).gender(g)). That is, you give each parameter a name by wrapping it into a function whose name matches that of the parameter. The entire list of named parameters is really a composition of function calls separated by a dot ("."). Thus, if the function takes a mix of mandatory and named parameters, you use a comma to separate the last non-named parameter from the first named parameters, like this:
When you use named parameters, the ordering is irrelevant, so f(name(n).age(a).gender(g)) is equivalent to f(age(a).gender(g).name(n)), and you can just omit any named parameter that has a default value.
The sequence of named parameters should start with CGAL::parameters::.
Below is a sample call of a function that uses the optional BGL named parameters.
This package provides the necessary classes and functions that enable using CGAL data structures as models of the Bgl graph concepts. To this end, we offer partial specializations of the boost::graph_traits<Graph> for various CGAL packages. For each such package, denoted PACKAGE, the partial specializations live in the namespace boost and are located in the header file CGAL/boost/graph/graph_traits_PACKAGE.h. Free functions are in the namespace CGAL, and the compiler uses argument-dependent lookup to find them. Euler operations, described in Section Euler Operations, are in the namespace CGAL::Euler, as the function remove_face() is at the same time a low-level and an Euler operation. Concerning the naming conventions, we have to use those of the Bgl, as to fulfill the requirements of the concepts defined in the Bgl.
Note that these partial specializations are often providing more than is required, making these classes not only models of the graph concepts of the Bgl, but also models of the CGAL graph concepts, that will be described in detail in Section Extensions of the BGL. Correspondence tables between the types of a CGAL data structure and their Bgl equivalents can be found in the Specializations of boost::graph_traits documentation page.
We present in the following sections some examples of utilization of some CGAL data structures as Bgl graphs.
The class Surface_mesh is a model of most of the graph concepts of the Bgl as well as the concepts provided by CGAL. A complete list can be found in the documentation of boost::graph_traits . The examples show how to use some of the Bgl algorithms with Surface_mesh and show how to use the concepts provided by CGAL to implement a simple algorithm.
The following example program computes the minimum spanning tree on a surface mesh. More examples can be found in Chapters Triangulated Surface Mesh Simplification, Triangulated Surface Mesh Segmentation, and Triangulated Surface Mesh Deformation.
The surface mesh class uses integer indices to address vertices and edges, and it comes with a built-in property mechanism that maps nicely on the Bgl.
File BGL_surface_mesh/prim.cpp
The class Polyhedron_3 is a model of most of the graph concepts of the Bgl as well as the concepts provided by CGAL. A complete list can be found in the documentation of boost::graph_traits . The examples show how to use some of the Bgl algorithms with Polyhedron_3 and show how to use the concepts provided by CGAL to implement a simple algorithm.
The following example program computes the minimum spanning tree on a polyhedral surface. More examples can be found in the Chapter Triangulated Surface Mesh Simplification.
File BGL_polyhedron_3/kruskal.cpp
The following example program shows a call to the Bgl Kruskal's minimum spanning tree algorithm accessing the id() field stored in a polyhedron vertex.
The main function illustrates the access to the id() field.
File BGL_polyhedron_3/kruskal_with_stored_id.cpp
Triangulations have vertices and faces, allowing for a direct translation as a graph. A halfedge is defined as a pair of a face handle and the index of the edge. A complete list can be found in the documentation of boost::graph_traits .
A classical example for an algorithm that is a combination of computational geometry and graph theory is the Euclidean Minimum Spanning Tree for a point set in the plane. It can be computed by running the minimum spanning tree algorithm on a Delaunay triangulation of the point set.
In the following example we create a Delaunay triangulation and run Kruskal's minimum spanning tree algorithm on it. Because the vertex handles of the triangulation are not indices in an array, we have to provide a property map that maps vertex handles to integers in the range [0, t.number_of_vertices()).
File BGL_triangulation_2/emst.cpp
The algorithms of the Bgl extensively use of the indices of vertices. In the previous example we stored the indices in a std::map and turned that map in a property map. This property map was then passed as argument to the shortest path function.
If the user does not pass explicitly a property map, the graph algorithms use the property map returned by the call get(boost::vertex_index,ft). This property map assumes that the vertex has a member function id() that returns a reference to an int. Therefore CGAL offers a class Triangulation_vertex_base_with_id_2. It is in the user's responsibility to set the indices properly.
The example further illustrates that the graph traits also works for the Delaunay triangulation.
File BGL_triangulation_2/dijkstra_with_internal_properties.cpp
CGAL offers a partial specialization of the boost graph traits for its arrangement class as well as for its dual graph.
Arrangement instances are adapted to boost graphs by specializing the boost:graph_traits template for Arrangement_2 instances. The graph-traits states the graph concepts that the arrangement class models (see below) and defines the types required by these concepts.
In this specialization the Arrangement_2 vertices correspond to the graph vertices, where two vertices are adjacent if there is at least one halfedge connecting them. More precisely, Arrangement_2::Vertex_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. As halfedges are directed, we consider the graph to be directed as well. Moreover, as several interior-disjoint \( x\)-monotone curves (say circular arcs) may share two common endpoints, inducing an arrangement with two vertices that are connected with several edges, we allow parallel edges in our boost graph.
Given an Arrangement_2 instance, we can efficiently traverse its vertices and halfedges. Thus, the arrangement graph is a model of the concepts VertexListGraph and EdgeListGraph introduced by the Bgl. At the same time, we use an iterator adapter of the circulator over the halfedges incident to a vertex (Halfedge_around_target_circulator - see Section Traversal Methods for an Arrangement Vertex of the chapter on arrangements), so it is possible to go over the ingoing and outgoing edges of a vertex in linear time. Thus, our arrangement graph is a model of the concept BidirectionalGraph (this concept refines IncidenceGraph, which requires only the traversal of outgoing edges).
It is important to notice that the vertex descriptors we use are Vertex_handle objects and not vertex indices. However, in order to gain more efficiency in most Bgl algorithm, it is better to have them indexed \( 0, 1, \ldots, (n-1)\), where \( n\) is the number of vertices. We therefore introduce the Arr_vertex_index_map<Arrangement> class-template, which maintains a mapping of vertex handles to indices, as required by the Bgl. An instance of this class must be attached to a valid arrangement vertex when it is created. It uses the notification mechanism (see Section The Notification Mechanism) to automatically maintain the mapping of vertices to indices, even when new vertices are inserted into the arrangement or existing vertices are removed.
A complete description of the types correspondences can be found in the documentation of boost::graph_traits .
In most algorithm provided by the Bgl, the output is given by property maps, such that each map entry corresponds to a vertex. For example, when we compute the shortest paths from a given source vertex \( s\) to all other vertices we can obtain a map of distances and a map of predecessors - namely for each \( v\) vertex we have its distance from \( s\) and a descriptor of the vertex that precedes \( v\) in the shortest path from \( s\). If the vertex descriptors are simply indices, one can use vectors to efficiently represent the property maps. As this is not the case with the arrangement graph, we offer the Arr_vertex_property_map<Arrangement,Type> template allows for an efficient mapping of Vertex_handle objects to properties of type Type. Note however that unlike the Arr_vertex_index_map class, the vertex property-map class is not kept synchronized with the number of vertices in the arrangement, so it should not be reused in calls to the Bgl functions in case the arrangement is modified in between these calls.
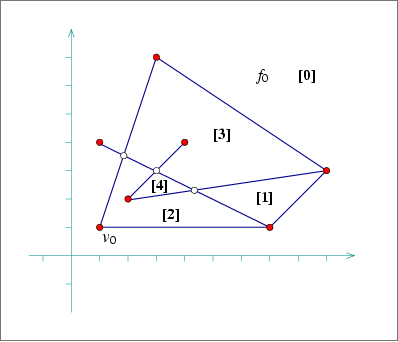
ex_bgl_primal_adapter.cpp and ex_bgl_dual_adapter.cpp. The breadth-first visit times for the arrangement faces, starting from the unbounded face \( f_0\), are shown in brackets. In the following example we construct an arrangement of 7 line segments, as shown in Figure 98.1, then use the Bgl Dijkstra's shortest-paths algorithm to compute the graph distance of all vertices from the leftmost vertex in the arrangement \( v_0\). Note the usage of the Arr_vertex_index_map and the Arr_vertex_property_map classes. The latter one, instantiated by the type double is used to map vertices to their distances from \( v_0\).
File BGL_arrangement_2/primal.cpp
It is possible to give a dual graph representation for an arrangement instance, such that each arrangement face corresponds to a graph vertex and two vertices are adjacent iff the corresponding faces share a common edge on their boundaries. This is done by specializing the boost:graph_traits template for Dual<Arrangement_2> instances, where Dual<Arrangement_2> is a template specialization that gives a dual interpretation to an arrangement instance.
In dual representation, Arrangement_2::Face_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. We treat the graph edges as directed, such that a halfedge e is directed from \( f_1\), which is its incident face, to \( f_2\), which is the incident face of its twin halfedge. As two arrangement faces may share more than a single edge on their boundary, we allow parallel edges in our boost graph. As is the case in the primal graph, the dual arrangement graph is also a model of the concepts VertexListGraph, EdgeListGraph and BidirectionalGraph (thus also of IncidenceGraph).
Since we use Face_handle objects as the vertex descriptors, we define the Arr_face_index_map<Arrangement> class-template, which maintains an efficient mapping of face handles to indices. We also provide the template Arr_face_property_map<Arrangement,Type> for associating arbitrary data with the arrangement faces.
In the following example we construct the same arrangement as in example ex_bgl_primal_adapter.cpp (see Figure 34.29), and perform breadth-first search on the graph faces, starting from the unbounded face. We extend the Dcel faces with an unsigned integer, marking the discover time of the face and use a breadth-first-search visitor to obtain these times and update the faces accordingly:
File BGL_arrangement_2/arrangement_dual.cpp
The previous sections introduced partial specializations and free functions so that several CGAL data structures are adapted as models of some of the Bgl graph concepts. In this section, we introduce new concepts, iterators, and property maps inspired by the functionalities of the Bgl.
In order to match Halfedge Data Structures more closely and to enable writing generic algorithms which operate on data structures that have faces and halfedges, we define a set of new concepts to extend the graph concepts of the BGL:
HalfedgeGraph refines Graph with operations to accommodate halfedge data structures: given a halfedge, say h, the concept HalfedgeGraph requires the provision of the halfedge opposite to h, the halfedge that succeeds h, and the halfedge that precedes h.HalfedgeListGraph adds the requirement for efficient traversal of the halfedges of the graph.MutableHalfedgeGraph adds the requirement for operations to change next/previous relations and to adjust the target of a halfedge.FaceGraph adds the requirements to explicitly handle faces in a graph, to provide quick access to the incident halfedges of a face, and to enable access from every halfedge to an adjacent face.FaceListGraph adds the requirement for efficient traversal of the faces of a graph.MutableFaceGraph adds requirements to change adjacency of faces and halfedges, and to remove and add faces.A summary of the expressions and types associated with each of these concepts as well as a refinement relation graph can be found in the Concepts documentation page.
By combining basic operations on graphs, we create various useful iterators and circulators to traverse specific types of elements. For example:
h of a halfedge graph g, applying several times next(h,g) brings us back to the halfedge where we started. All halfedges traversed on the way are incident to the same face.next(h,g) and opposite(h,g) results in another cycle, namely the cycle of halfedges which are incident to the same vertex.A complete list of these traversal tools can be found in the reference manual.
For convenience, two iterator and circulator types enable the traversal of all halfedges incident to a given face, and all halfedges having a given vertex as target. These types are not part of the concept HalfedgeGraph, but they are class templates that work for any model of this concept.
The following example shows several functions to navigate in a HalfedgeGraph. We have two implementations of the operation that finds the vertices adjacent to a vertex v.
Let us have a look at the first version. Given a vertex descriptor vd, we first call halfedge(vd,g) to obtain the halfedge with vd as target. Applying source() then gives us an adjacent vertex. We then get to the next halfedge with vd as target, by first going to the next halfedge around the face, and then going to the opposite halfedge.
The second version does the next() and opposite() jumping with an iterator. Note that when calling source() we have to dereference hi, as the function expects a halfedge descriptor and not a halfedge iterator. Also observe that halfedges_around_target() expects a halfedge, and not a vertex. This provides the user with the ability to start the traversal at a specific halfedge incident to the input vertex (and not the arbitrary incident halfedge stored in the vertex record.)
File BGL_polyhedron_3/incident_vertices.cpp
The following example program shows a simple algorithm for calculating facet normals for a polyhedron using the Bgl API. A boost::vector_property_map is used to to store the calculated normals instead of changing the Polyhedron items class.
File BGL_polyhedron_3/normals.cpp
As the concepts HalfedgeGraph and FaceGraph add the notion of halfedges and faces, as well as a geometric embedding of the vertices, we have to add property tags such as face_index_t and vertex_point_t.
We further add dynamic properties that enable the user to add properties to vertices, halfedges, edges, and faces on the fly. The lifetime of a dynamic property is bound to the lifetime of the property map: reference counting is used to delete the property when no map refers to it.
Dynamic property tags, such as dynamic_vertex_property_t, are a generalization of boost::vertex_index_t, as they have a template parameter for the value type of the dynamic property map, and a default value. boost::property_map<G,T>::type is used to obtain the type of the dynamic property map for a graph of type G, for a dynamic property tag T. This type must be default constructible and assignable. As for ordinary properties, the function get() is overloaded and serves for retrieving a property map for a given graph and dynamic property tag, as well as for retrieving a value for a given key and property map.
The following example shows how to attach a string property to vertices and a double value to the halfedges of a graph.
File Property_map/dynamic_properties.cpp
There are two categories of mutating operations. The first category comprises low level operations that change incidences such as the target vertex of a halfedge. A halfedge graph might turn invalid by the application of inconsistent low lever operations. The second category of operations are called Euler Operations. These are high level operations such as adding a center vertex to a face, which means also adding halfedges and faces, and updating incidence information. The Euler operations enable manipulating models of MutableFaceGraph.
The complete list of Euler operations provided by this package can be found in the reference manual.
Graph adaptors are classes that build an interface over an existing graph to provide new functionalities. By operating almost entirely on the input graph, adaptors can avoid potentially expensive operations, both in term of time and memory.
The dual graph of a FaceGraph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge. Thus, each edge e of G has a corresponding dual edge, the edge that connects the two faces on either side of e. Computing the dual graph of a graph has many uses, for example when one wishes to compute the connected components of a mesh.
The class template Dual is an adaptor that creates the dual view of a FaceGraph. Faces of the original graph correspond to vertices in the Dual and vice versa.
Note that border edges in a Dual have the null_face of the original graph as either source or target. This is unusual and might break other algorithms since edges are always assumed to have non-null vertices as a source and target. It is nevertheless possible to filter border edges using boost::filtered_graph, as shown in the following example.
File BGL_surface_mesh/surface_mesh_dual.cpp
The class Seam_mesh allows to mark edges of a mesh as seam edges so that they virtually become border edges when exploring a seam mesh with the Bgl API. The input mesh is referred to as underlying mesh of the seam mesh. We denote tm and sm the underlying mesh and the seam mesh respectively.
Figure Figure 98.2 shows an example of mesh on which two edges, defined by the halfedge pairs h2-h3 and h6-h7, are marked as seams. The introduction of virtual borders modifies the elementary Bgl graph traversal operations: when we circulate around the target of h7 in the underlying mesh, we traverse h7, h1, h3, h5, before arriving at h7 again. However, when we circulate in the seam mesh, we traverse h7, h1, h3*, before arriving at h7 again. Similarly, if we start at h3, we traverse h3, h5, h7*, and h3 again.
A vertex of the underlying mesh may correspond to multiple vertices in the seam mesh. For example in Figure Figure 98.2, the target of h7 corresponds to two vertices in the seam mesh, on either side of the virtual border created by the seam edges. For this reason, a vertex v of the seam mesh is internally represented as a halfedge h of the seam mesh. To obtain a canonical definition, the halfedge h is defined as the halfedge that has v as target, that lies on the seam, and that is not a border halfedge. The function target(hd, sm) will return this halfedge. For vertices v in the underlying mesh that are not on a seam edge, we choose halfedge(v, tm) as its canonical halfedge.
Using the function next(halfedge_descriptor, FaceGraph), we can walk around a face but also around a border of a mesh. For the seam mesh sm from Figure Figure 98.2, we have opposite(h2, sm) == h3*, and it holds that face(h3*, sm) == null_face(). We can walk along this virtual border: starting at h3* and repeatedly calling next(..,sm), we will traverse h6*, h7*, h2*, before reaching h3* again.
All other traversal functions, iterators, and circulators (see Iterators and Circulators) can be used on a seam mesh, but their behavior is similarly modified by the (virtual and real) border edges of the seam mesh.
A collection of seam edges, or simply a seam, is not necessarily a simple polyline as we can see in the next figure:
v on the border of the underlying mesh. While walking along the border of the seam mesh, we leave the border of the underlying mesh when we reach v and walk on a virtual border until we reach v again, from the other side of the seam. Seam meshes are for example used in Chapter Triangulated Surface Mesh Parameterization to parameterize a topological sphere by first virtually cutting it into a topological disk.
For algorithms that operate locally, partitioning is often an easy way to parallelize the algorithm at little cost. The functions CGAL::METIS::partition_graph() and CGAL::METIS::partition_dual_graph() provide wrappers to the graph partitioning library METIS [3], allowing to split triangular meshes that are models of the concept FaceListGraph into a given number of subdomains.
The following example shows how to read, partition, and write a mesh using partition_dual_graph(). The class template CGAL::Face_filtered_graph and the free function copy_face_graph() are used to create an independent mesh from one of the subdomains of the partition. Note that the copy is optional as writing can be done directly using Face_filtered_graph.
File BGL_surface_mesh/surface_mesh_partition.cpp
Using Named Parameters some of the many options of METIS can be customized, as shown in this example.
An optimal partition from a set of labels can be computed through a graph cut approach called alpha expansion [1]. CGAL provides CGAL::alpha_expansion_graphcut() which, for a graph \((V,E)\), computes the partition f that minimizes the following cost function:
\[ \mathrm{C}(f) = \sum_{\{v0,v1\} \in E} C_E(v0,v1) + \sum_{v \in V} C_V(f_v) \]
where \(C_E(v0,v1)\) is the edge cost of assigning a different label to \(v0\) and \(v1\), and \(C_V(f_v)\) is the vertex cost of assigning the label \(f\) to the vertex \(v\).
Three different implementations are provided and can be selected by using one of the following tags:
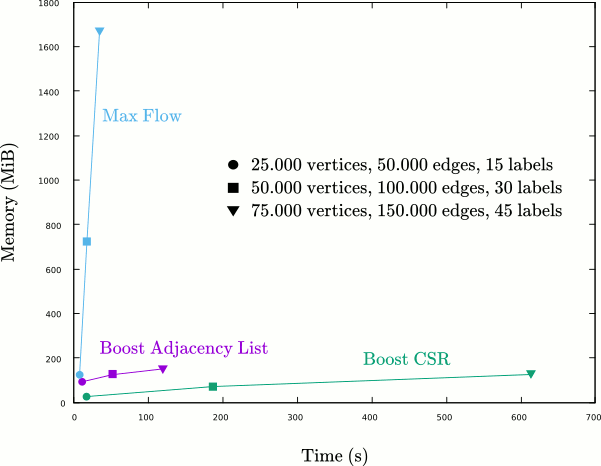
CGAL::Alpha_expansion_boost_adjacency_list_tag (default)CGAL::Alpha_expansion_boost_compressed_sparse_raw_tagCGAL::Alpha_expansion_MaxFlow_tag, released under GPL license and provided by the Triangulated Surface Mesh Segmentation Reference packageAll these implementations produce the exact same result but behave differently in terms of timing and memory (see Figure 98.4). The MaxFlow implementation is the fastest, but it grows rapidly in memory when increasing the complexity of the input graph and labeling; the compressed sparse raw (CSR) is very efficient from a memory point of view but becomes very slow as the complexity of the input graph and labeling increases; the adjacency list version provides a good compromise and is therefore the default implementation.
The following example shows how to apply the alpha expansion algorithm to a boost::adjacency_list describing a 2D array with 3 labels "X", " " and "O":
File BGL_graphcut/alpha_expansion_example.cpp
The output of this program shows how the initial 2D array is regularized spatially:
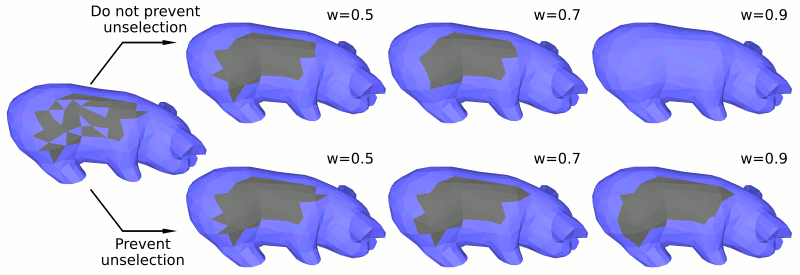
Manually selecting faces on a triangle mesh may create irregular borders (sawtooth) because of the shape of the triangles. Such borders can be regularized using the alpha expansion algorithm.
CGAL provides a function CGAL::regularize_face_selection_borders() to apply this algorithm to the borders of a face selection on a FaceGraph. Figure 98.5 shows how this function affects a selection depending on the parameters.
The following example shows how to apply this alpha expansion regularization to the borders of a face selection of a CGAL::Surface_mesh object:
File BGL_graphcut/face_selection_borders_regularization_example.cpp