|
CGAL 5.1.5 - Planar Parameterization of Triangulated Surface Meshes
|
|
CGAL 5.1.5 - Planar Parameterization of Triangulated Surface Meshes
|
Parameterizing a surface amounts to finding a one-to-one mapping from a suitable domain to the surface. A good mapping is the one which minimizes either angle distortions (conformal parameterization) or area distortions (equiareal parameterization) in some sense. In this package, we focus on parameterizing triangulated surfaces which are homeomorphic to a disk or a sphere, and on piecewise linear mappings onto a planar domain.
Although the main motivation behind the first parameterization methods was the application to texture mapping, it is now frequently used for mapping more sophisticated modulation signals (such as normal, transparency, reflection or light modulation maps), fitting scattered data, re-parameterizing spline surfaces, repairing CAD models, approximating surfaces and remeshing.
This CGAL package implements surface parameterization methods, such as As Rigid As Possible Parameterization, Tutte Barycentric Mapping, Discrete Authalic Parameterization, Discrete Conformal Maps, Least Squares Conformal Maps, Floater Mean Value Coordinates, or Orbifold Tutte Embeddings. These methods mainly distinguish by the distortion they minimize (angles vs. areas), by the constrained border onto the planar domain (convex polygon vs. free border) and by the bijectivity guarantees of the mapping.
The package proposes an interface for any model of the concept FaceGraph, such as the classes Surface_mesh, Polyhedron_3, Seam_mesh, or the mesh classes of OpenMesh.
Seam_mesh can be used to virtually cut a mesh, allowing to transform an input mesh in subdomain(s) that fit the disk-or-sphere topology requirement.Since parameterizing meshes requires an efficient representation of sparse matrices and efficient iterative or direct linear solvers, we provide a unified interface to linear solvers as described in Chapter CGAL and Solvers.
Note that linear solvers commonly use double precision floating point numbers. Therefore, this package is intended to be used with a CGAL Cartesian kernel with doubles.

From the user point of view, the simplest entry point to this package is the following function:
The function parameterize() applies a default surface parameterization method, namely Floater Mean Value Coordinates [4] (see Section Floater Mean Value Coordinates), to the connected component of the mesh of type TriangleMesh with the border given by the halfedge bhd. This border is parameterized with an arc-length circular border parameterization. The sparse linear solver of the Eigen library is used.
The mesh of type TriangleMesh must be a model of the concept FaceGraph and must additionally be triangulated, 2-manifold, oriented, and homeomorphic to a disc (possibly with holes). The last requirement is not hard and we will later show how to parameterize a mesh that is not a topological disk (Section Cutting a Mesh). The result is stored in a property map (whose type is here VertexUVMap) for the mesh vertices. See also Chapter CGAL and Boost Property Maps.
In the following example, we apply the default parameterization (Floater Mean Value Coordinates) to a Surface_mesh mesh. We store the UV-coordinates as a vertex property using the Surface_mesh built-in property mechanism.
File Surface_mesh_parameterization/simple_parameterization.cpp
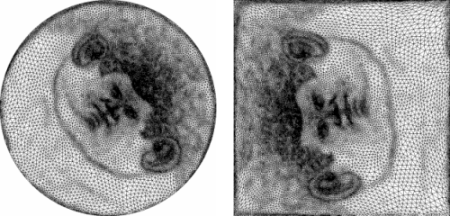
Figure Figure 70.2 illustrates the input and output of this program.

This package provides a second parameterize() entry point where the user can specify a parameterization method:
It computes a one-to-one mapping from a 3D triangle surface mesh to a simple 2D domain. The mapping is piecewise linear on the triangle mesh. The result is a pair (u,v) of parameter coordinates for each vertex of the input mesh. A one-to-one mapping may be guaranteed or not, depending on the choice of the Parameterizer_3 algorithm.
In the following example, we use the Discrete Authalic parameterizer with a circular border parameterization. We use a Surface_mesh for the mesh and store the UV-coordinates as a vertex property using the Surface_mesh built-in property mechanism.
File Surface_mesh_parameterization/discrete_authalic.cpp
Other parameterization methods can easily be swapped in by simply replacing the lines
with other compatible border and domain parameterizers, e.g.
Which border and which domain parameterizers can be combined is explained in the next section.
This CGAL package implements surface parameterization methods, such as As Rigid as Possible, Tutte Barycentric, Discrete Authalic Parameterization, Discrete Conformal Map, Least Squares Conformal Maps, Floater Mean Value Coordinates, or Orbifold Tutte Embeddings. These methods are provided as models of the Parameterizer_3 concept.
The different parameterization methods can be classified into three categories depending on the type of border parameterization that is required: fixed border, free border, and borderless.
Illustrations of the different methods are obtained with the same input model, the hand model, shown in Figure Figure 70.3. The hand is a topological sphere, and a Seam_mesh is used to cut it into a topological disk. In Figure Figure 70.3, the seam is traced in red and the four cones used for Orbifold Tutte Parameterization (Section Orbifold Tutte Embeddings) are marked with green dots.
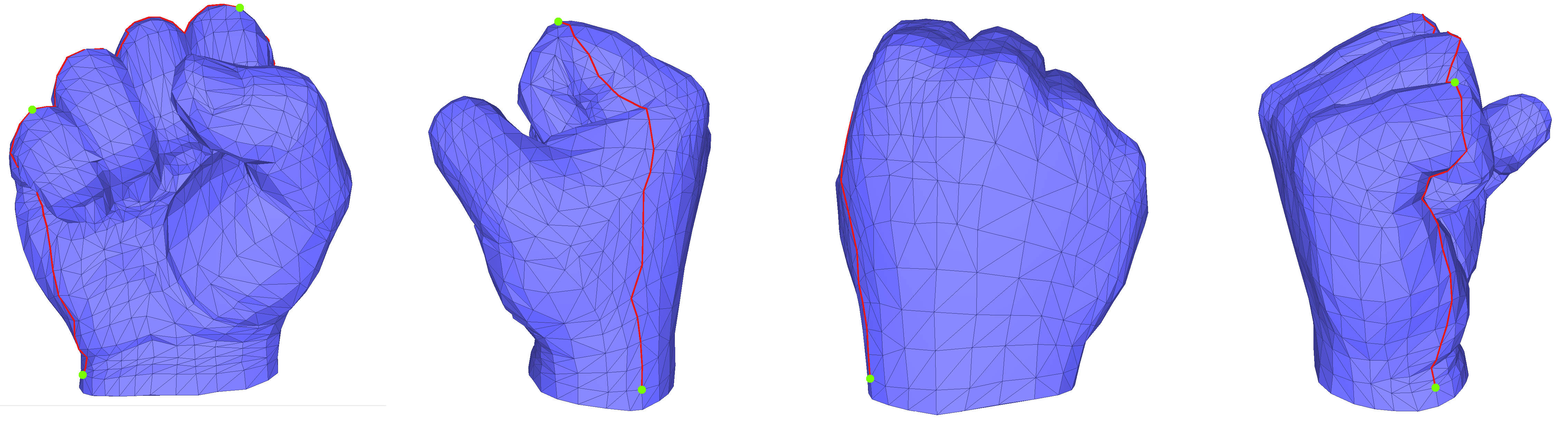
Fixed border surface parameterizations are characterized by having a constrained border in parameter space: two (u,v) coordinates for each vertex along the border. Different choices exist for such border parameterization methods, described in Section Border Parameterizations for Fixed Methods.
Surface_mesh_parameterization::Barycentric_mapping_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
The Barycentric Mapping parameterization method has been introduced by Tutte [10]. In parameter space, each vertex is placed at the barycenter of its neighbors to achieve the so-called convex combination condition. This algorithm amounts to solve one sparse linear system for each set of parameter coordinates, with a #vertices x #vertices sparse and symmetric positive definite matrix (if the border vertices are eliminated from the linear system). A coefficient \( (i, j)\) of the matrix is set to 1 for an edge linking the vertex \( v_i\) to the vertex \( v_j\), to minus the degree of the vertex \( v_i\) for a diagonal element, and to 0 for any other matrix entry. Although a bijective mapping is guaranteed when the border is convex, this method does not minimize either angle nor area distortion.

Surface_mesh_parameterization::Discrete_authalic_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
The Discrete Authalic parameterization method has been introduced by Desbrun et al. [2]. It corresponds to a weak formulation of an area-preserving method, and in essence locally minimizes the area distortion. A one-to-one mapping is guaranteed only if the convex combination condition is fulfilled and the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is asymmetric.

Surface_mesh_parameterization::Discrete_conformal_map_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
Discrete Conformal Map parameterization has been introduced to the graphics community by Eck et al. [3]. It attempts to lower angle deformation by minimizing a discrete version of the Dirichlet energy as derived by Pinkall and Polthier [9]. A one-to-one mapping is guaranteed only when the two following conditions are fulfilled: the barycentric mapping condition (each vertex in parameter space is a convex combination of its neighboring vertices), and the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is sparse and symmetric positive definite (if the border vertices are eliminated from the linear system and if the mesh contains no hole), and thus can be efficiently solved using dedicated linear solvers.

Surface_mesh_parameterization::Mean_value_coordinates_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
The Mean Value Coordinates parameterization method has been introduced by Floater [4]. Each vertex in parameter space is optimized to be a convex combination of its neighboring vertices. This method is in essence an approximation of the Discrete Conformal Map, with a guaranteed one-to-one mapping when the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is asymmetric.

Parameterization methods for borders are used as traits classes modifying the behavior of Parameterizer_3 models. They are also provided as models of the Parameterizer_3 concept. Border parameterizations for fixed border surface parameterizations are a family of methods to define a set of constraints, namely two \( u,v\) coordinates for each vertex along the border.
Different choices are offered to the user when choosing border parameterizers for fixed border methods:
The user can select a border parameterization among two commonly used methods: uniform or arc-length parameterization.
Usage: Uniform border parameterizations are more stable, although they yield poor visual results. The arc-length border parameterization is used by default.
One convex shape specified by one shape among two standard ones: a circle or a square.
Usage: The circular border parameterization is used by default as it corresponds to the simplest convex shape. The square border parameterization is commonly used for texture mapping.
All combinations of uniform/arc-length and circle/square are provided by the following classes:
Surface_mesh_parameterization::Circular_border_arc_length_parameterizer_3<TriangleMesh> Surface_mesh_parameterization::Circular_border_uniform_parameterizer_3<TriangleMesh> Surface_mesh_parameterization::Square_border_arc_length_parameterizer_3<TriangleMesh> Surface_mesh_parameterization::Square_border_uniform_parameterizer_3<TriangleMesh> An illustration of the use of different border parameterizers can be found in the example square_border_parameterizer.cpp.
For free border parameterization methods, the vertices of the border are free to move.
Surface_mesh_parameterization::LSCM_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
The Least Squares Conformal Maps (LSCM) parameterization method has been introduced by Lévy et al. [7]. It corresponds to a conformal method with a free border (at least two vertices have to be constrained to obtain a unique solution), which allows further lowering of the angle distortion. A one-to-one mapping is not guaranteed by this method. It solves a (2 \( \times\) #triangles) \( \times\) #vertices sparse linear system in the least squares sense, which implies solving a symmetric matrix.

Surface_mesh_parameterization::ARAP_parameterizer_3<TriangleMesh, BorderParameterizer, SolverTraits>
An as-rigid-as-possible parameterization was introduced by Liu et al. [8]. It is a shape-preserving method based on an iterative energy minimization process. Each step alternates a local optimization technique to find the best local mapping and a global stitching technique equivalent to the resolution of a linear system to guarantee that the parameterized mesh is a triangulation.
A generalization of the formulation of the local optimization introduces a scalar coefficient λ that allows the user to balance angle and shape distortion: the closer λ is to 0, the more importance is given to the minimization of angle distortion; inversely, when λ grows, the parameterizer gives more and more importance to the minimization of shape distortion.

Parameterization methods for borders are used as traits classes modifying the behavior of Parameterizer_3 models. They are also provided as models of the Parameterizer_3 concept. The border parameterizations associated to free border surface parameterization methods define only two constraints: the pinned vertices.
Surface_mesh_parameterization::Two_vertices_parameterizer_3<TriangleMesh>
Usage: Surface_mesh_parameterization::Two_vertices_parameterizer_3<TriangleMesh> is the default free border parameterization, and is the only one available in the current version of this package.
Borderless parameterization methods do not require as input a mesh that is homeomorphic to a disk.
Surface_mesh_parameterization::Orbifold_Tutte_parameterizer_3<SeamMesh, SolverTraits>
Orbifold-Tutte Planar Embedding was introduced by Aigerman and Lipman [1] and is a generalization of Tutte’s embedding to other topologies, and in particular spheres, which we consider here. The orbifold-Tutte embedding bijectively maps the original surface, that is required to be a topological ball, to a canonical, topologically equivalent, two-dimensional flat surface called an Euclidean orbifold. There are 17 Euclidean orbifolds, of which only the 4 sphere orbifolds are currently implemented in CGAL.
The orbifold-Tutte embedding yields a seamless, globally bijective parameterization that, similarly to the classic Tutte embedding, only requires solving a sparse linear system for its computation.
The algorithm requires the user to select a set of vertices of the input mesh and mark them as cones, which will be the singularities of the unfolding. Internally, the process requires the use of (virtual) seams between the cones, but the choice of these seams does not influence the result. The Seam_mesh structure (see also Section Cutting a Mesh) is used for this purpose.

The surface parameterization methods proposed in this package only deal with meshes which are homeomorphic (topologically equivalent) to discs. Nevertheless, meshes with arbitrary topology and number of connected components can be parameterized, provided that the user specifies a cut graph (a set of edges), which defines the border of a topological disc. These edges can be passed together with a mesh via the Seam_mesh structure.
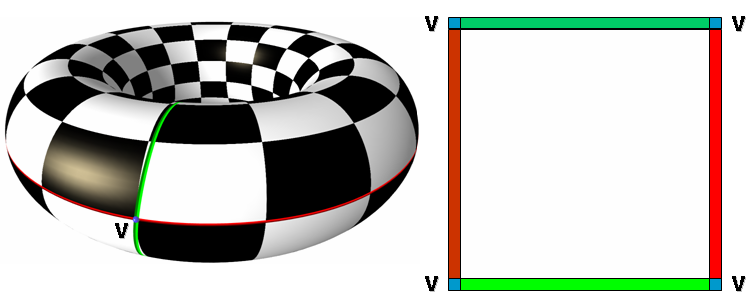
In the following example, we apply the default parameterization to a Polyhedron_3-based Seam_mesh. We store the UV-coordinates as a halfedge property using a Unique_hash_map.
Note that vertices on a seam are duplicated in a Seam_mesh structure and thus the UV-coordinates are here associated to the halfedges of the underlying (input) mesh.
File Surface_mesh_parameterization/seam_Polyhedron_3.cpp
Fixed boundaries
One-to-one mapping
Tutte's theorem guarantees a one-to-one mapping provided that the weights are all positive and the border is convex. It is the case for Tutte Barycentric Mapping and Floater Mean Value Coordinates. It is not always the case for Discrete Conformal Map (cotangents) and Discrete Authalic parameterization.
Non-singularity of the matrix
Geshorgin's theorem guarantees the convergence of the solver if the matrix is diagonal dominant. This is the case with positive weights (Tutte Barycentric Mapping and Floater Mean Value Coordinates).
Free boundaries
One-to-one mapping
No guarantee is provided by either LSCM or ARAP parameterizations (both global overlaps and triangle flips can occur).
Non-singularity of the matrix
For LSCM, the matrix of the system is the Gram matrix of a matrix with maximal rank, and is therefore non-singular (Gram theorem).
Boundary-less
One-to-one mapping
The Orbifold-Tutte embedding is guaranteed to exist and to be computable via a sparse linear system.
The main author of the first version of this package was Laurent Saboret, who worked as an engineer at Inria Sophia-Antipolis under the supervision of Pierre Alliez and Bruno Lévy. Bruno Lévy added OpenNL support to the package.
For CGAL 4.11, the package has undergone a major rewrite by Andreas Fabri and Mael Rouxel-Labbé. The As-Rigid-As-Possible parameterization technique was added and all algorithms are now based on the FaceGraph API. The Orbifold Tutte Embedding parameterization technique was also added with the help of its authors, Noam Aigerman and Yaron Lipman. Finally, the class Seam_mesh was introduced to handle virtual borders. The class Seam_mesh is also a model of a FaceGraph, and replaces a wrapper which had a more complicated API.