|
CGAL 5.2.2 - 2D Voronoi Diagram Adaptor
|
|
CGAL 5.2.2 - 2D Voronoi Diagram Adaptor
|
This chapter describes an adaptor that adapts two-dimensional triangulated Delaunay graphs to the corresponding Voronoi diagrams. We start with a few definitions and a description of the issues that this adaptor addresses in Section Introduction. The software design of the Voronoi diagram adaptor package is described in Section Software Design. In Section The Adaptation Traits we discuss the traits required for performing the adaptation, and finally in Section Examples we present a few examples using this adaptor.
A Voronoi diagram is typically defined for a set of objects, also called sites in the sequel, that lie in some space \( \Sigma\) and a distance function that measures the distance of a point \( x\) in \( \Sigma\) from an object in the object set. In this package we are interested in planar Voronoi diagrams, so in the sequel the space \( \Sigma\) will be the space \( \mathbb{R}^2\). Let \( \mathcal{S}=\{S_1,S_2,\ldots,S_n\}\) be our set of sites and let \( \delta(x,S_i)\) denote the distance of a point \( x\in\mathbb{R}^2\) from the site \( S_i\). Given two sites \( S_i\) and \( S_j\), the set \( V_{ij}\) of points that are closer to \( S_i\) than to \( S_j\) with respect to the distance function \( \delta(x,\cdot)\) is simply the set:
\[ V_{ij} = \{x\in\mathbb{R}^2:\, \delta(x,S_i)<\delta(x,S_j)\}. \]
We can then define the set \( V_i\) of points on the plane that are closer to \( S_i\) than to any other object in \( \mathcal{S}\) as:
\[ V_i = \bigcap_{i\neq j} V_{ij}. \]
The set \( V_i\) is said to be the Voronoi cell or Voronoi face of the site \( S_i\). The locus of points on the plane that are equidistant from exactly two sites \( S_i\) and \( S_j\) is called a Voronoi bisector. A point that is equidistant to three or more objects in \( \mathcal{S}\) is called a Voronoi vertex. A simply connected subset of a Voronoi bisector is called a Voronoi edge. The collection of Voronoi faces, edges and vertices is called the Voronoi diagram of the set \( \mathcal{S}\) with respect to the distance function \( \delta(x,\cdot)\), and it turns out that it is a subdivision of the plane, i.e., it is a planar graph.
We typically think of faces as 2-dimensional objects, edges as 1-dimensional objects and vertices as 0-dimensional objects. However, this may not be the case for several combinations of sites and distance functions (for example points in \( \mathbb{R}^2\) under the \( L_1\) or the \( L_\infty\) distance can produce 2-dimensional Voronoi edges). We call a Voronoi diagram nice if no such artifacts exist, i.e., if all vertices edges and faces are 0-, 1- and 2-dimensional, respectively.
Even nice Voronoi diagrams can end up being not so nice. The cell of a site can in general consist of several disconnected components. Such a case can happen, for example, when we consider weighted points \( Q_i=(p_i,\lambda_i)\), where \( p_i\in\mathbb{R}^2\), \( \lambda_i\in\mathbb{R}\), and the distance function is the Euclidean distance multiplied by the weight of each site, i.e., \( \delta_M(x,Q_i)=\lambda_i\,\|x-p_i\|\), where \( \|\cdot\|\) denotes the Euclidean norm. In this package we are going to restrict ourselves to nice Voronoi diagrams that have the property that the Voronoi cell of each site is a simply connected region of the plane. We are going to call such Voronoi diagrams simple Voronoi diagrams. Examples of simple Voronoi diagrams include the usual Euclidean Voronoi diagram of points, the Euclidean Voronoi diagram of a set of disks on the plane (i.e., the Apollonius diagram), the Euclidean Voronoi diagram of a set of disjoint convex objects on the plane, or the power or (Laguerre) diagram for a set of circles on the plane. In fact every instance of an abstract Voronoi diagram in the sense of Klein [1] is a simple Voronoi diagram in our setting. In the sequel when we refer to Voronoi diagrams we will refer to simple Voronoi diagrams.
In many cases we are not really interested in computing the Voronoi diagram itself, but rather its dual graph, called the Delaunay graph. In general the Delaunay graph is a planar graph, each face of which consists of at least three edges. Under the non-degeneracy assumption that no point on the plane is equidistant, under the distance function, to more than three sites, the Delaunay graph is a planar graph with triangular faces. In certain cases this graph can actually be embedded with straight line segments in which case we talk about a triangulation. This is the case, for example, for the Euclidean Voronoi diagram of points, or the power diagram of a set of circles. The dual graphs are, respectively, the Delaunay triangulation and the regular triangulation of the corresponding site sets. Graphs of non-constant non-uniform face complexity can be undesirable in many applications, so typically we end up triangulating the non-triangular faces of the Delaunay graph. Intuitively this amounts to imposing an implicit or explicit perturbation scheme during the construction of the Delaunay graph, that perturbs the input sites in such a way so as not to have degenerate configurations.
Choosing between computing the Voronoi diagram or the (triangulated) Delaunay graph is a major decision while implementing an algorithm. It heavily affects the design and choice of the different data structures involved. Although in theory the two approaches are entirely equivalent, it is not so straightforward to go from one representation to the other. The objective of this package is to provide a generic way of going from triangulated Delaunay graphs to planar subdivisions represented through a DCEL data structure. The goal is to provide an adaptor that gives the look and feel of a DCEL data structure, although internally it keeps a graph data structure representing triangular graphs.
The adaptation might seem straightforward at a first glance, and more or less this is case; after all one graph is the dual of the other. The situation becomes complicated whenever we want to treat artifacts of the representation used. Suppose for example that we have a set of sites that contains subsets of sites in degenerate positions. The computed triangulated Delaunay graph has triangular faces that may be the result of an implicit or explicit perturbation scheme. The dual of such a triangulated Delaunay graph is a Voronoi diagram that has all its vertices of degree 3, and for that purpose we are going to call it a degree-3 Voronoi diagram in order to distinguish it from the true Voronoi diagram of the input sites. A degree-3 Voronoi diagram can have degenerate features, namely Voronoi edges of zero length, and/or Voronoi faces of zero area. Although we can potentially treat such artifacts, they are nonetheless artifacts of the algorithm we used and do not correspond to the true geometry of the Voronoi diagram.
The manner that we treat such issues in this package in a generic way is by defining an adaptation policy. The adaptation policy is responsible for determining which features in the degree-3 Voronoi diagram are to be rejected and which not. The policy to be used can vary depending on the application or the intended usage of the resulting Voronoi diagram. What we care about is that firstly the policy itself is consistent and, secondly, that the adaptation is also done in a consistent manner. The latter is the responsibility of the adaptor provided by this package, whereas the former is the responsibility of the implementor of a policy.
In this package we currently provide two types of adaptation policies. The first one is the simplest: we reject no feature of the degree-3 Voronoi diagram; we call such a policy an identity policy since the Voronoi diagram produced is identical to the degree-3 Voronoi diagram. The second type of policy eliminates the degenerate features from the degree-3 Voronoi diagram yielding the true geometry of the Voronoi diagram of the input sites; we call such policies degeneracy removal policies.
Delaunay graphs can be mutable or non-mutable. By mutable we mean that sites can be inserted or removed at any time, in an entirely on-line fashion. By non-mutable we mean that once the Delaunay graph has been created, no changes, with respect to the set of sites defining it, are allowed. If the Delaunay graph is a non-mutable one, then the Voronoi diagram adaptor is a non-mutable adaptor as well.
If the Delaunay graph is mutable then the question of whether the Voronoi diagram adaptor is also mutable is slightly more complex to answer. As long as the adaptation policy used does not maintain a state, the Voronoi diagram adaptor is a mutable one; this is the case, for example, with our identity policy or the degeneracy removal policies. If, however, the adaptor maintains a state, then whether it is mutable or non-mutable really depends on whether its state can be updated after every change in the Delaunay graph. Such policies are our caching degeneracy removal policies: some of them result in mutable adaptors others result in non-mutable ones. In Section The Adaptation Policy we discuss the issue in more detail.
The Voronoi_diagram_2<DG,AT,AP> class is parameterized by three template parameters. The first one must be a model of the DelaunayGraph_2 concept. It corresponds to the API required by an object representing a Delaunay graph. All classes of CGAL that represent Delaunay diagrams are models of this concept, namely, Delaunay triangulations, regular triangulations, Apollonius graphs and segment Delaunay graphs. The second template parameter must be a model of the AdaptationTraits_2 concept. We discuss this concept in detail in Section The Adaptation Traits. The third template parameter must be model of the AdaptationPolicy_2 concept, which we discuss in detail in Section The Adaptation Policy.
The Voronoi_diagram_2<DG,AT,AP> class has been intentionally designed to provide an API similar to the arrangements class in CGAL: Voronoi diagrams are special cases of arrangements after all. The API of the two classes, however, could not be identical. The reason is that arrangements in CGAL do not yet support more than one unbounded faces, or equivalently, cannot handle unbounded curves. On the contrary, a Voronoi diagram defined over at least two generating sites, has at least two unbounded faces.
On a more technical level, the Voronoi_diagram_2<DG,AT,AP> class imitates the representation of the Voronoi diagram (seen as a planar subdivision) by a DCEL (Doubly Connected Edge List) data structure. We have vertices (the Voronoi vertices), halfedges (oriented versions of the Voronoi edges) and faces (the Voronoi cells). In particular, we can basically perform every operation we can perform in a standard DCEL data structure:
In addition to the above possibilities for traversal, we can also traverse the following features through iterators:
Finally, depending on the adaptation traits passed to the Voronoi diagram adaptor, we can perform point location queries, namely given a point \( p\) we can determine the feature of the Voronoi diagram (vertex, edge, face) on which \( p\) lies.
The AdaptationTraits_2 concept defines the types and functors required by the adaptor in order to access geometric information in the Delaunay graph that is needed by the Voronoi_diagram_2<DG,AT,AP> class. In particular, it provides functors for accessing sites in the Delaunay graph and constructing Voronoi vertices from their dual faces in the Delaunay graph. Finally, it defines a tag that indicates whether nearest site queries are to be supported by the Voronoi diagram adaptor. If such queries are to be supported, a functor is required.
Given a query point, the nearest site functor should return information related to how many and which sites of the Voronoi diagram are at equal and minimal distance from the query point. In particular, if the query point is closest to a single site, the vertex handle of the Delaunay graph corresponding to this site is returned. If the query point is closest to exactly two site, the edge of the Delaunay graph that is dual to the Voronoi edges on which the query point lies is returned. If three (or more) sites are closest to the query point, then the query point coincides with a vertex in the Voronoi diagram, and the face handle of the face in the Delaunay graph that is dual to the Voronoi vertex is returned. This way of abstracting the point location mechanism allows for multiple different point location strategies, which are passed to the Voronoi diagram adaptor through different models of the AdaptationTraits_2 concept. The point location and nearest sites queries of the Voronoi_diagram_2<DG,AT,AP> class use internally this nearest site query functor.
In this package we provide four adaptation traits classes, all of which support nearest site queries:
Apollonius_graph_adaptation_traits_2<AG2> class: it provides the adaptation traits for Apollonius graphs. Delaunay_triangulation_adaptation_traits_2<DT2> class: it provides the adaptation traits for Delaunay triangulations. Regular_triangulation_adaptation_traits_2<RT2> class: it provides the adaptation traits for regular triangulations. Segment_Delaunay_graph_adaptation_traits_2<SDG2> class: it provides the adaptation traits for segment Delaunay graphs. As mentioned above, when we perform the adaptation of a triangulated Delaunay graph to a Voronoi diagram, a question that arises is whether we want to eliminate certain features of the Delaunay graph when we construct its Voronoi diagram representation (such features could be the Voronoi edges of zero length or, for the Voronoi diagram of a set of segments forming a polygon, all edges outside the polygon). The manner that we treat such issues in this package in a generic way is by defining an adaptation policy. The adaptation policy is responsible for determining which features in the degree-3 Voronoi diagram are to be rejected and which not. The policy to be used can vary depending on the application or the intended usage of the resulting Voronoi diagram.
The concept AdaptationPolicy_2 defines the requirements on the predicate functors that determine whether a feature of the triangulated Delaunay graph should be rejected or not. More specifically it defines an Edge_rejector and a Face_rejector functor that answer the question: "Should this
edge (face) of the Voronoi diagram be rejected?". In addition to the edge and face rejectors the adaptation policy defines a tag, the Has_inserter tag. This tag is either set to CGAL::Tag_true or to CGAL::Tag_false. Semantically it determines if the adaptor is allowed to insert sites in an on-line fashion (on-line removals are not yet supported). In the former case, i.e., when on-line site insertions are allowed, an additional functor is required, the Site_inserter functor. This functor takes a reference to a Delaunay graph and a site, and inserts the site in the Delaunay graph. Upon successful insertion, a handle to the vertex representing the site in the Delaunay graph is returned.
We have implemented two types of policies that provide two different ways for answering the question of which features of the Voronoi diagram to keep and which to discard. The first one is called the identity policy and corresponds to the Identity_policy_2<DG,VT> class. This policy is in some sense the simplest possible one, since it does not reject any feature of the Delaunay graph. The Voronoi diagram provided by the adaptor is the true dual (from the graph-theoretical point of view) of the triangulated Delaunay graph adapted. This policy assumes that the Delaunay graph adapted allows for on-line insertions, and the Has_inserter tag is set to Tag_true. A default site inserter functor is also provided.
The second type of policy we provide is called degeneracy removal policy. If the set of sites defining the triangulated Delaunay graph contains subsets of sites in degenerate configurations, the graph-theoretical dual of the triangulated Delaunay graph has edges and potentially faces that are geometrically degenerate. By that we mean that the dual of the triangulated Delaunay graph can have Voronoi edges of zero length or Voronoi faces/cells of zero area. Such features may not be desirable and ideally we would like to eliminate them. The degeneracy removal policies eliminate exactly these features and provide a Voronoi diagram where all edges have non-zero length and all cells have non-zero area. More specifically, in these policies the Edge_rejector and Face_rejector functors reject the edges and vertices of the Delaunay graph that correspond to dual edges and faces that have zero length and area, respectively. In this package we provide four degeneracy removal policies, namely:
Apollonius_graph_degeneracy_removal_policy_2<AG2> class: it provides an adaptation policy for removing degeneracies when adapting an Apollonius graph to an Apollonius diagram. Delaunay_triangulation_degeneracy_removal_policy_2<DT2> class: it provides an adaptation policy for removing degeneracies when adapting a Delaunay triangulation to a point Voronoi diagram. The Regular_triangulation_degeneracy_removal_policy_2<RT2> class: it provides an adaptation policy for removing degeneracies when adapting a regular triangulation to a power diagram
Segment_Delaunay_graph_degeneracy_removal_policy_2<SDG2> class: it provides an adaptation policy for removing degeneracies when adapting a segment Delaunay graph to a segment Voronoi diagram. A variation of the degeneracy removal policies are the caching degeneracy removal policies. In these policies we cache the results of the edge and face rejectors. In particular, every time we want to determine, for example, if an edge of the Delaunay graph has, as dual edge in the Voronoi diagram, an edge of zero length, we check if the result has already been computed. If yes, we simply return the outcome. If not, we perform the necessary geometric tests, compute the answer, cache it and return it. Such a policy really pays off when we have a lot of degenerate data in our input set of sites. Verifying whether a Voronoi edge is degenerate or not implies computing the outcome of a predicate in a possibly degenerate or near degenerate configuration, which is typically very costly (compared to computing the same predicate in a generic configuration). To avoid this cost every single time we want to check if a Voronoi edge is degenerate or not, we compute the result of the geometric predicate the first time the adaptor asks for it, and simply lookup the answer in the future. In this package we provide four caching degeneracy removal policies, one per degeneracy removal policy mentioned above. Intentionally, we have not indicated the value of the Has_inserter tag for the degeneracy removal and caching degeneracy removal policies. The issue is discussed in detail in the sequel.
We raised the question above, as to whether the adaptor is a mutable or non-mutable one, in the sense of whether we can add/remove sites in an on-line fashion. The answer to this question depends on: (1) whether the Delaunay graph adapted allows for on-line insertions/removals and (2) whether the adaptation policies maintains a state and whether this state is easily maintainable when we want to allow for on-line modifications.
The way we indicate if we allow on-line insertions of sites is via the Has_inserter tag (as mentioned, on-line removals are currently not supported). The Has_inserter tag has two possible values, namely, Tag_true and Tag_false. The value Tag_true indicates that the Delaunay graph allows for on-line insertions, whereas the value Tag_false indicates the opposite. Note that these values do not indicate if the Delaunay graph supports on-line insertions, but rather whether the Voronoi diagram adaptor should be able to perform on-line insertions or not. This delicate point will be become clearer below.
Let us consider the various scenarios. If the Delaunay graph is non-mutable, the Voronoi diagram adaptor cannot perform on-line insertions of sites. In this case not only degeneracy removal policies, but rather every single adaptation policy for adapting the Delaunay graph in question should have the Has_inserter tag set to Tag_false.
If the Delaunay graph is mutable, i.e., on-line site insertions as are allowed, we can choose between two types of adaptation policies, those that allow these on-line insertions and those that do not. In the former case the Has_inserter tag should be set to Tag_true, whereas in the latter to Tag_false. In other words, even if the Delaunay graph is mutable, we can choose (by properly determining the value of the Has_inserter tag) if the adaptor should be mutable as well. At a first glance it may seem excessive to restrict existing functionality. There are situations, however, where such a choice is necessary.
Consider a caching degeneracy removal policy. If we do not allow for on-line insertions then the cached quantities are always valid since the Voronoi diagram never changes. If we allow for on-line insertions the Voronoi diagram can change, which implies that the results of the edge and faces degeneracy testers that we have cached are no longer valid or relevant. In these cases, we need to somehow update these cached results, and ideally we would like to do this in an efficient manner. The inherent dilemma in the above discussion is whether the Voronoi diagram adaptor should be able to perform on-line insertions of sites. The answer to this question in this framework is given by the Has_inserter tag. If the tag is set to Tag_false the adaptor cannot insert sites on-line, whereas if the tag is set to Tag_true the adaptor can add sites on-line. In other words, the Has_inserter tag determines how the Voronoi diagram adaptor should behave, and this is enough from the adaptor's point of view.
From the point of a view of a policy writer the dilemma is still there: "Should the policy allow for on-line insertions or not?" The answer really depends on what are the consequences of such a choice. For a policy that has no state, such as our degeneracy removal policies, it is natural to set the Has_inserter tag to Tag_true. For our caching degeneracy removal policies, our choice was made on the grounds of whether we can update the cached results efficiently when insertions are performed. For CGAL's Apollonius graphs, Delaunay triangulation and regular triangulations it is possible to ask what are the edges and faces of the Delaunay graph that are to be destroyed when a query site is inserted. This is done via the get_conflicts method provided by these classes. Using the outcome of the get_conflicts method the site inserter can first update the cached results (i.e., indicate which are invalidated) and then perform the actual insertion. Such a method does not yet exist for segment Delaunay graphs. We have thus chosen to support on-line insertions for all non-caching degeneracy removal policies. The caching degeneracy removal policy for segment Delaunay graphs does not support on-line insertions, whereas the remaining three caching degeneracy removal policies support on-line insertions.
One last item that merits some discussion are the different choices from the point of view of time- and space-efficiency.
As far as the Voronoi diagram adaptor is concerned, only a copy of the adaptation traits and a copy of the adaptation policy are stored in it. The various adaptation traits classes we provide are empty classes (i.e., they do not store anything). The major time and space efficiency issues arise from the various implementations of the adaptation policies. Clearly, the identity policy has no dominant effect on neither the time or space efficiency. The costs when choosing this policy are due to the underlying Delaunay graph.
The non-caching degeneracy removal policies create a significant time overhead since every time we want to access a feature of the Voronoi diagram, we need to perform geometric tests in order to see if this feature or one of its neighboring ones has been rejected. Such a policy is acceptable if we know we are away from degeneracies or for small input sizes. In the case of the segment Delaunay graph, it is also the only policy we provide that at the same time removes degeneracies and allows for on-line insertion of sites. Caching policies seem to be the best choice for moderate to large input sizes (1000 sites and more). They do not suffer from the problem of dealing with degenerate configurations, but since they cache the results, they increase the space requirements by linear additive factor. To conclude, if the user is interested in getting a Voronoi diagram without degenerate features and knows all sites in advance, the best course of action is to insert all sites at construction time and use a caching degeneracy removal policy. This strategy avoids the updates of the cached results after each individual insertion, due to the features of the Voronoi diagram destroyed because of the site inserted.
In this section we present an example that shows how to perform point location queries.
File Voronoi_diagram_2/vd_2_point_location.cpp
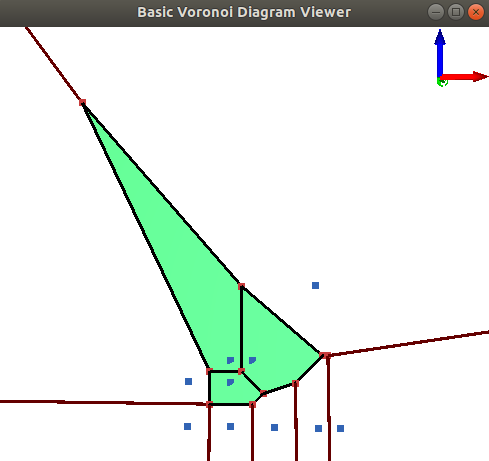
A 2D Voronoi Diagram can be visualized by calling the CGAL::draw<VD>() function as shown in the following example. This function opens a new window showing the Voronoi Diagram of the given input sites/vertix locations. A call to this function is blocking, that is the program continues as soon as the user closes the window.
This function requires CGAL_Qt5, and is only available if the flag CGAL_USE_BASIC_VIEWER is defined at compile time.
File Voronoi_diagram_2/draw_voronoi_diagram_2.cpp