
 |
Although they are represented in a canonical form by only two vertices, namely the lexicographically smallest and largest vertex with respect to Cartesian coordinates, we provide functions for ``accessing'' the other vertices as well.
Iso-oriented cuboids and bounding boxes are quite similar. The difference however is that bounding boxes have always double coordinates, whereas the coordinate type of an iso-oriented cuboid is chosen by the user.
|
| |||
|
introduces an iso-oriented cuboid c with diagonal
opposite vertices and . Note that the object is
brought in the canonical form.
| |||
| |||
|
introduces an iso-oriented cuboid c whose
minimal coordinate is the one of left, the
maximal coordinate is the one of right, the
minimal coordinate is the one of bottom, the
maximal coordinate is the one of top, the
minimal coordinate is the one of far, the
maximal coordinate is the one of close.
| |||
| |||
|
introduces an iso-oriented cuboid c with diagonal
opposite vertices
(min_hx/hw, min_hy/hw, min_hz/hw) and
(max_hx/hw, max_hy/hw, max_hz/hw). Precondition: hw 0.
| |||
|
|
| |
| Test for equality: two iso-oriented cuboid are equal, iff their lower left and their upper right vertices are equal. | ||
|
|
| |
| Test for inequality. | ||
|
|
| returns the i'th vertex modulo 8 of c. starting with the lower left vertex. |
|
|
| |
| returns vertex(i), as indicated in the figure below: | ||
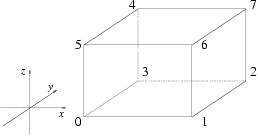
|
|
| returns the smallest vertex of c (= vertex(0)). |
|
|
| returns the largest vertex of c (= vertex(7)). |
|
|
| returns smallest Cartesian -coordinate in c. |
|
|
| returns smallest Cartesian -coordinate in c. |
|
|
| returns smallest Cartesian -coordinate in c. |
|
|
| returns largest Cartesian -coordinate in c. |
|
|
| returns largest Cartesian -coordinate in c. |
|
|
| returns largest Cartesian -coordinate in c. |
|
|
| |
|
returns -th
Cartesian
coordinate of
the smallest vertex of c. Precondition: . | ||
|
|
| |
|
returns -th
Cartesian
coordinate of
the largest vertex of c. Precondition: . | ||
|
|
| c is degenerate, if all vertices are collinear. |
|
|
| |
| returns either ON_UNBOUNDED_SIDE, ON_BOUNDED_SIDE, or the constant ON_BOUNDARY, depending on where point is. | ||
|
|
| |
|
|
| |
|
|
| |
|
|
| returns the volume of c. |
|
|
| returns a bounding box containing c. |
|
| ||
|
| ||
|
returns the iso-oriented cuboid obtained by applying on
the smallest and the largest of c. Precondition: The angle at a rotation must be a multiple of , otherwise the resulting cuboid does not have the same size. Note that rotating about an arbitrary angle can even result in a degenerate iso-oriented cuboid. | ||