Chapter 17
Topological Maps

17.1   Introduction

17.2   Basic Terms and Software Design

The Planar_map_2<Dcel,Traits> class (Chapter ) is derived from the Topological_map<Dcel> class and it describes an embedding of a topological map in the Euclidean plane. This chapter and Chapter describe the Topological_map class and the Planar_map class respectively. These classes supply the ability to maintain subdivisions of the plane induced by collections of curves. In this chapter we introduce the topological map. In this section we briefly review the concepts underlying the data structures described in the following sections as well as the functionality of Topological_map in a nutshell.

Figure:  A face, an edge, and a vertex

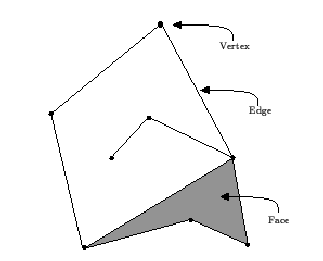
Topological Map, Vertex, Edge, Face: A topological map is a graph that consists of vertices V, edges E, faces F and an incidence relation on them. Each edge is represented by two halfedges with opposite orientations. A face of the topological map is defined by the ordered circular sequences (inner and outer) of halfedges along its boundary.

Incidence: If a vertex $$v is an endpoint of an edge $$e, then we say that $$v and $$e are incident to each other. Similarly, a face and an edge on its boundary are incident, and a face and a vertex on its boundary are incident (including edges and vertices that are not connected to the outer boundary - see below).

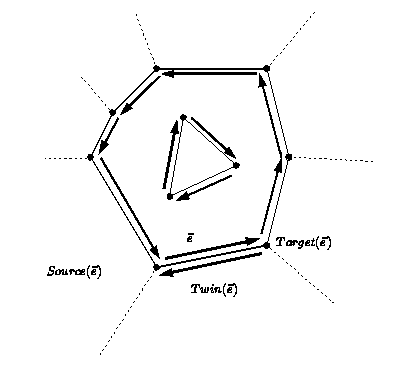
Halfedge, Twin, Source, Target: We consider each edge $$e to be two-sided, representing it by two directed halfedges $$e and $$Twin(e) (In other packages the twin halfedge is called $$opposite). A halfedge $$e is an ordered pair $$(u,v) of its endpoints, and it is directed from $$u, the source, to $$v, the target (there is no need to store both in each halfedge since $$Target(e) Source(Twin(e))). We consider each halfedge to lie on the boundary of a single face.

Connected Component of the Boundary (CCB): Each connected component of the boundary of a face is defined by a circular list of halfedges. For a face $$f of a topological map, we call each connected component of the boundary of $$f a CCB. A bounded face has a unique CCB that is defined to be its outer CCB. An unbounded face does not have an outer boundary. In the topological map we have one unbounded face. Except for the outer CCB, any other connected component of the boundary of $$f is called a hole (or inner CCB), every face can have none or several holes. We say that the holes are contained inside the face.

Edges around a Vertex : Every maximal set of halfedges that share the same target can be viewed as a circular list of halfedges ordered around their target vertex. It should be noted that the orientation of the edges around a vertex is opposite to that of the halfedges around a face, i.e., if edge $$e2 succeeds edge $$e1 in the order given around vertex $$v, then $$e1 succeeds $$e2 in the order given around the incident face $$f. Unlike the convention we adopt for Planar_map in Chapter  where the halfedges are oriented counterclockwise around a face and clockwise around a vertex, in the topological map the users are free to choose any other convention.

Figure:  Source and target vertices, and twin halfedges

Doubly Connected Edge List (DCEL): For a topological map, its DCEL representation consists of a connected list of halfedges for every CCB of every face in the subdivision, with additional incidence information that enables us to traverse the subdivision. For each halfedge the DCEL stores a pointer to its twin halfedge and to the next halfedge around its incident face (see Figure ). In addition, for each halfedge the DCEL stores a pointer to the incident face and the target vertex. For each face the DCEL stores a pointer to a halfedge representing its outer-CCB and an iterator over pointers to halfedges representing its inner-CCBs (traversing over a CCB is thus done with repetitive calls to the next halfedge pointer). For each vertex the DCEL stores a pointer to an incident halfedge. For more information about the DCEL representation see  [dBvKOS97] and Chapter  on Halfedge_data_structure. The DCEL is a low-level container class that stores the objects. The topological map layer adds high-level functions and protection of combinatorial validity. Iterators, handles and circulators are also introduced in this layer (pointers are no longer visible in this layer).

In the following specifications, we implement the subdivision by a DCEL.

Functionality

The class Topological_map<Dcel> supplies the ability to maintain a topological map. The user can insert edges in various ways and then split, merge or remove them as well as move holes from one face to another. The vertices, edges and faces can be traversed in a linear way or any other fashion mentioned above. For a full reference of the class (i.e its associated types, its operations, etc.) read the Topological_map Reference Pages.

17.3   Example Programs

17.3.1   Simple Topological Map

The function is_valid() checks the validity of the topological map.

// file: examples/Topological_map/example1.C

#include <CGAL/basic.h>
#include <iostream>

#include <CGAL/Topological_map_bases.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Topological_map.h>


typedef CGAL::Pm_dcel<CGAL::Tpm_vertex_base,
                      CGAL::Tpm_halfedge_base,
                      CGAL::Tpm_face_base> Dcel;  

typedef CGAL::Topological_map<Dcel> Tpm;

typedef Tpm::Halfedge_handle Halfedge_handle;
typedef Tpm::Vertex_handle   Vertex_handle;
typedef Tpm::Face_handle     Face_handle;

int main()
{

  Tpm t;

  Face_handle uf = t.unbounded_face();

  std::cout << "Inserting edge e1 in unbounded face interior ... " ;
  Halfedge_handle e1 = t.insert_in_face_interior(uf);
  CGAL_assertion(t.is_valid());
  std::cout << "map is valid!" << std::endl;

  std::cout << "Inserting edge e2 from target vertex of e1 ... " ;
  Halfedge_handle e2 = t.insert_from_vertex(e1);
  CGAL_assertion(t.is_valid());
  std::cout <<  "map is valid!" << std::endl;

  std::cout << "Inserting edge e3 between target vertices of e2 and twin of "
            << "e1 ... ";

  t.insert_at_vertices(e2,e1->twin());

  CGAL_assertion(t.is_valid());
  std::cout << "map is valid!" << std::endl;

  return 0;
}

The output of the program is:

inserting edge e1 in face interior ...map is valid.
inserting edge e2 from target vertex of e1 ...map is valid.
inserting edge e3 between target vertices of e2 and e1->twin() ...map is valid.

17.3.2   Topological Map with Additional Information

// file: examples/Topological_map/example2.C

#include <CGAL/basic.h>
#include <iostream>

#include <CGAL/Topological_map_bases.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Topological_map.h>

class Face_with_info : public CGAL::Tpm_face_base {
  int inf;
public:
  Face_with_info() : CGAL::Tpm_face_base(), inf(0) {}

  int info() { return inf; }
  void set_info(int i) { inf = i; }
};

typedef CGAL::Pm_dcel<CGAL::Tpm_vertex_base,
                      CGAL::Tpm_halfedge_base,
                      Face_with_info > Dcel;  

typedef CGAL::Topological_map<Dcel> Tpm;

typedef Tpm::Halfedge_handle Halfedge_handle;
typedef Tpm::Vertex_handle   Vertex_handle;
typedef Tpm::Face_handle     Face_handle;

int main()
{
  
  Tpm t;

  Face_handle uf = t.unbounded_face();

  Halfedge_handle e1 = t.insert_in_face_interior(uf);
  CGAL_assertion(t.is_valid());
  std::cout << "Edge e1 inserted in unbounded face interior" << std::endl;

  Halfedge_handle e2 = t.insert_from_vertex(e1);
  CGAL_assertion(t.is_valid());
  std::cout << "Edge e2 inserted from target vertex of e1" << std::endl;

  Halfedge_handle e3 = t.insert_at_vertices(e2, e1->twin());
  CGAL_assertion(t.is_valid());
  std::cout << "Edge e3 inserted between target vertices of e2 and "
            << "twin of e1" << std::endl;
  
  std::cout << std::endl <<"Setting info of the new face to 10" << std::endl;
  Face_handle nf = e3->face();
  nf->set_info(10);

  std::cout << "Unbounded face info = " << uf->info() << std::endl;
  std::cout << "New face info = " << nf->info() << std::endl;

  return 0;
}

The output of the program is:

inserting e1 in face interior...
inserting e2 from vertex...
inserting e3 between vertices of e2 and e1->twin()...

setting info of the new face to 10...

unbounded face info = 0
new face info = 10