Planar maps are embeddings of topological maps into the plane. A planar map subdivides the plane into vertices, edges, and faces. The vertices, edges, and faces of a subdivision are the embeddings of their topological map counterparts into the plane, such that (1) each vertex is embedded as a planar point, (2) each edge is embedded as a bounded -monotone curve, and does not contain vertices in its interior, and (3) each face is a maximal connected region of the plane that does not contain edges and vertices in its interior.
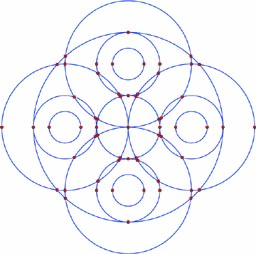
Figure: A planar map induced by 14 circles of 53 faces (one of which is unbounded), 106 edges, and 59 vertices.
The Planar_map_2<Dcel,Traits> class is derived from the Topological_map<Dcel> class. While the Topological_map<Dcel> base class provides the necessary combinatorial-related capabilities, the Planar_map_2<Dcel,Traits> class provides all the geometric-related capabilities required to maintain planar maps of interior-disjoint -monotone curves, and perform geometric queries, such as point location.
In this chapter we review the data and functionality added
to the Planar_map_2<Dcel,Traits> class over that of the
Topological_map<Dcel> class. The combinatorial capabilities of
the base class are covered in chapter 
,
Topological Maps.
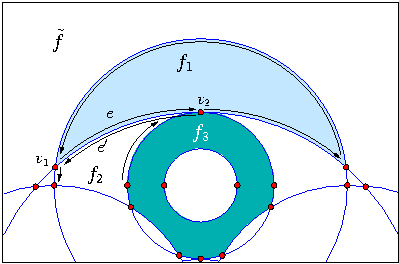
Figure: A portion of the planar map depicted in Figure with some of the DCEL records that represent it. is the unbounded face. The half-edge (and its twin ) correspond to a circular arc that connects the vertices and and separates the face from . The predecessors and successors of and are also shown - note that , together with its predecessor and successor half-edges form a closed chain representing the boundary of (lightly shaded). Also note that the face (darkly shaded) has a more complicated structure as it contains a hole in its interior.
#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Pm_segment_traits_2.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Planar_map_2.h>
typedef CGAL::Quotient<CGAL::MP_Float> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Pm_segment_traits_2<Kernel> Traits;
typedef Traits::Point_2 Point_2;
typedef Traits::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Pm_default_dcel<Traits> Dcel;
typedef CGAL::Planar_map_2<Dcel,Traits> Planar_map;
int main()
{
Planar_map pm;
X_monotone_curve_2 cv[3];
Point_2 a1(0,0), a2(0,4), a3(4,0);
cv[0] = X_monotone_curve_2(a1,a2);
cv[1] = X_monotone_curve_2(a2,a3);
cv[2] = X_monotone_curve_2(a3,a1);
pm.insert(&cv[0], &cv[3]);
return 0;
}
The constructed planar map is instantiated with the Pm_segment_traits_2 traits class to handle segments only. It consists of two faces, a triangular face and the unbounded face. This program is not very useful, as it ends immediately after the planar map is constructed. Let us add something useful, such as querying whether a point is located in the interior of the single face of our planar map. All we need to do is issue the following statements:
Point_2 p(1,1);
typedef Planar_map::Locate_type lt;
(void) pm.locate(p, lt);
if (lt != Planar_map::FACE)
std::cout << "Point location failed!" << std::endl;
else
std::cout << "Point location passed!" << std::endl;
The information returned from the locate() function is not analyzed further, as this program is presented to illustrates a simple usage only.
Let us make our simple example a bit more interesting, and draw the planar map with Qt, as exemplified in the code fragments below. First, we must add the following include directives:
#include <qapplication.h>
#include <CGAL/IO/Qt_widget.h>
#include <CGAL/IO/Pm_Window_stream.h>
Next, we create a Qt widget:
QApplication app(argc, argv); CGAL::Qt_widget widget; app.setMainWidget(widget); widget.resize(400,400); widget.set_window(-0.5, 4.5, -0.5, 4.5); widget.show();
Now, we can send the planar map to a Qt widget after constructing one::
ws << pm;
The combinatorial entities have a geometric mapping, e.g., a vertex of a planar map has a Point data member and a halfedge has a X_monotone_curve_2 (x-monotone curve) data member.
The Planar_map_2<Dcel,Traits> class consists of a three other components. (1) It includes a set of interface functions that allow you to construct, modify, query, save, and restore a planar map, (2) It is parameterized with a traits concept class that defines the abstract interface between planar maps and the primitives they use, and (3) some of its constructors allow you to choose between various point-location strategies. The point-location strategy has a significant impact not only on the performance of point-location queries, but also on the performance of the operations that modify the planar map.
for further information.
Insertion of a collection of -monotone curves into a planar map that is not empty is not supported yet. However, the aggregate insertion of a collection of curves into an empty map is drastically more efficient than the incremental insertion of the curves one at a time, as the aggregate insertion exploits a dedicated efficient sweep line algorithm. Notice, that the traits function curves_compare_y_at_x_left() is not required, nor are the point_reflect_in_x_and_y() and curve_reflect_in_x_and_y() functions, if aggregate insertion is the only modification performed and no queries are performed.
When additional information detailed below is available, special insertion function can be used to expedite the insertion of a single curve. This information may consists of one of the following: (1) the face containing the curve to be inserted, (2) the vertex containing a curve endpoint, (3) the two vertices containing the two curve endpoints respectively, or (4) the halfedges whose incident vertices contain the curve endpoints respectively. The time complexity of the insertion operation reduces to , when the incident halfedges are available and provided to the corresponding special insert function.
The code fragment listed below demonstrates the use of some of the special insertion-functions.
Planar_map pm; Point_2 a0(0, 0), a1(2, 0), a2(1, 2); X_monotone_curve_2 cv[3]; cv[0] = X_monotone_curve_2(a0, a1); cv[1] = X_monotone_curve_2(a1, a2); cv[2] = X_monotone_curve_2(a2, a0); Planar_map::Halfedge_handle e[3]; e[0] = pm.insert_in_face_interior(cv[0], pm.unbounded_face()); e[1] = pm.insert_from_vertex(cv[1], e[0]); e[2] = pm.insert_at_vertices(cv[2], e[1], e[0]->twin());
Two halfedges are constructed as a result of inserting a single curve into a planar map. One of the two new halfedges is returned from the applied function. The insert() and the insert_in_face_interior() insertion functions return the new halfedge directed in the same way as the input curve. There are two flavors of insert_from_vertex() and two falvours of insert_at_vertices() functions. One accepts vertices and the other accepts halfedges as additional information to expedite the insertion. These functions return the new halfedge directed according to the additional information, regardless of the input-curve direction. The insert_from_vertex() functions return the new halfedge that has the given vertex as its source vertex, when a vertex is provided. When a halfedge is provided instead of a vertex, the target vertex of the given halgedge is the source of the returned new halfedge. The insert_at_vertices() functions return the new halfedge, that has the given vertices as its source and target vertices respectively, when vertices are provided. When halfedges are provided instead of vertices, the target vertices of the given halgedges are the source and target of the returned new halfedge respectively.
The next example exploits the most efficient speacial insertion-functions, and
provided to untangle their subtleties. Figure contains
the drawing of the planar map generated by the code fragment listed below.
Figure: A planar map generated by special insertion functions
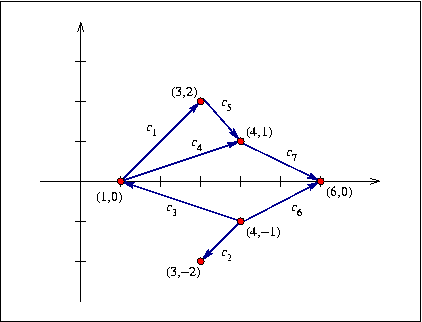
Planar_map pm; X_monotone_curve_2 cv1(Point_2(1.0, 0.0), Point_2(3.0, 2.0)); X_monotone_curve_2 cv2(Point_2(4.0, -1.0), Point_2(3.0, -2.0)); X_monotone_curve_2 cv3(Point_2(4.0, -1.0), Point_2(1.0, 0.0)); X_monotone_curve_2 cv4(Point_2(1.0, 0.0), Point_2(4.0, 1.0)); X_monotone_curve_2 cv5(Point_2(3.0, 2.0), Point_2(4.0, 1.0)); X_monotone_curve_2 cv6(Point_2(6.0, 0.0), Point_2(4.0, -1.0)); X_monotone_curve_2 cv7(Point_2(4.0, 1.0), Point_2(6.0, 0.0)); Halfedge_handle h1 = pm.insert_in_face_interior(cv1, pm.unbounded_face()); Halfedge_handle h2 = pm.insert_in_face_interior(cv2, pm.unbounded_face()); Halfedge_handle h3 = pm.insert_at_vertices(cv3, h2->twin(), h1->twin()); Halfedge_handle h4 = pm.insert_from_vertex(cv4, h1->twin()); Halfedge_handle h5 = pm.insert_at_vertices(cv5, h1, h4); Halfedge_handle h6 = pm.insert_from_vertex(cv6, h3->twin()); Halfedge_handle h7 = pm.insert_at_vertices(cv7, h5, h6);
In addition to the queries provided by the Topological_map<Dcel> base class, you can perform point location and vertical ray shoot queries, and find out whether a given point is contained in a given face.
The point location and vertical ray-shoot functions, namely
Figure contains
the drawing of the planar map generated by example1. This example issues
a vertical-ray shoot query illustrated in the figure as well. The code of this
program is listed below.
Figure: The map generated by example1
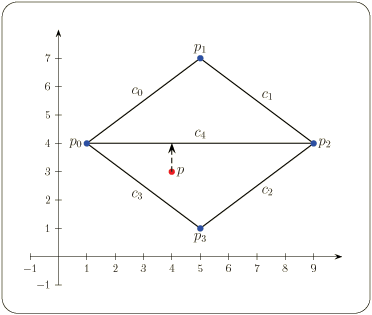
The constructed planar map is instantiated with the Pm_segment_traits_2 traits class to handle segments only. The traits class is instanciated in turn with the CGAL Cartesian kernel. The later is instanciated with the field of quotions of multi-precision floating-point as the number type. The planar map consists of five segments that induce three faces. After the construction of the map, its validity is verified, follwed by a vertical-ray shoot.
// file: examples/Planar_map/example1.C
#include "short_names.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/Pm_segment_traits_2.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Planar_map_2.h>
#include <iostream>
#include <iterator>
#include <algorithm>
typedef CGAL::Quotient<long> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Pm_segment_traits_2<Kernel> Traits;
typedef Traits::Point_2 Point_2;
typedef Traits::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Pm_default_dcel<Traits> Dcel;
typedef CGAL::Planar_map_2<Dcel,Traits> Planar_map;
int main()
{
// Create an instance of a Planar_map:
Planar_map pm;
X_monotone_curve_2 cv[5];
Point_2 p0(1, 4), p1(5, 7), p2(9, 4), p3(5, 1);
// Create the curves:
cv[0] = X_monotone_curve_2(p0, p1);
cv[1] = X_monotone_curve_2(p1, p2);
cv[2] = X_monotone_curve_2(p2, p3);
cv[3] = X_monotone_curve_2(p3, p0);
cv[4] = X_monotone_curve_2(p0, p2);
std::cout << "The curves of the map :" << std::endl;
std::copy(&cv[0], &cv[5],
std::ostream_iterator<X_monotone_curve_2>(std::cout, "\n"));
std::cout << std::endl;
// Insert the curves into the Planar_map:
std::cout << "Inserting the curves to the map ... ";
pm.insert(&cv[0], &cv[5]);
std::cout << ((pm.is_valid()) ? "map valid!" : "map invalid!") << std::endl
<< std::endl;
// Shoot a vertical ray upward from p:
Point_2 p(4, 3);
Planar_map::Locate_type lt;
std::cout << "Upward vertical ray shooting from " << p << std::endl;
Planar_map::Halfedge_handle e = pm.vertical_ray_shoot(p, lt, true);
std::cout << "returned the curve " << e->curve() << ", oriented toward "
<< e->target()->point() << std::endl;
return 0;
}
The output of the program is:
the curves of the map : 1/1 4/1 5/1 7/1 5/1 7/1 9/1 4/1 9/1 4/1 5/1 1/1 5/1 1/1 1/1 4/1 1/1 4/1 9/1 4/1 Inserting the curves to the map ... map valid! Upward vertical ray shooting from 4/1 3/1 returned the curve 1/1 4/1 9/1 4/1, oriented toward 1/1 4/1
A simple textual format of a planar map representation can be written to the standard output with the Extractor ( >> ) operator defined for Planar_map_2. The same format can be read from the standard input with the Inserter ( << ) operator defined for Planar_map_2. Add the include directive below to include these operator definitions,
#include <CGAL/IO/Pm_iostream.h>
Advanced formats, such as XML-based, are currently considered, but haven't been implemented yet, nor has a binary format.
With the use of the Pm_drawer class a planar map representation can be sent to a graphic stream, such as CGAL::Qt_widget, Postscript file, or Geomview window. Add the include directive below to include this class definition.
#include <CGAL/IO/Pm_drawer.h>
Drawing a planar map with Geomview or producing Postscript that represents a planar map, can be done by applying the Inserter operator to the appropriate graphic stream and the planar map instance. Add the corresponding include directive below, to include any if these class definitions.
#include <CGAL/IO/Pm_Postscript_file_stream.h>
#include <CGAL/IO/Pm_Geomview_stream.h>
If you intend to save, restore, or draw a planar map, you must define I/O operators for the point and curve types defined in your Traits classes, in case these operations are not present. The traits classes provided in the Planar Map packages, e.g., Pm_segment_traits_2 and Pm_conic_traits_2, contain the appropriate definitions to save a textual representation of a planar map to the standard output, restore it from the standard input, and draw it to a CGAL window stream.
| advanced |
|
If you wish to add your own attributes planar map components. If those attributes are to be written as part of the planar map representation (respectively, are to be re-read later) a specialized reader (scanner) class (writer class, resp.) should be defined for the special planar map. This is done preferably by making it a sub class of the class Pm_file_scanner (Pm_file_writer, resp.) and overriding all the relevant function for scanning (writing, resp.) the changed components.
After the definition of the inherited class, you have to call the function read of Planar map (resp., the global function write_pm ) with the inherited class as a parameter.
The same applies for extending the output graphic streams to include additional attributes only for this purpose a new drawer class has to be defined. This is done preferably by making this class inherit the class Pm_drawer. In order to send the special planar map to the graphic stream one should call the global function draw_pm with this class and their planar map as parameters.
Format The chosen format does not follow an existing standard format. Generally, the format contains lists of the components of a planar map followed by each other. For each component we write its associative geometric information and some topological information in order to be able to update the Dcel efficiently. The format is detailed below.
The current format may not be comfortable for a user to read because of the extensive use of indices. You can print a planar map in a verbose format (shorthand for verbose mode format). The skeleton of the verbose format is the same. However, in order for the output to be clearer for a human reader points and halfedges are explicitly written rather than being represented by indices. Also the direction of the halfedges are printed in a more convenient way to read. This verbose format cannot be scanned by the reading functions of Planar_map_2.
The example below presents a representation of a planar map containing one triangle with the coordinates (0,0), (1,1) and (2,0). The Planar_map_2 instance that was used to produce this example was templated with the Pm_segment_traits_2 class, which in turn was templated with the representation class Cartesian<leda_rational>. The first line specifies that the planar map has three vertices, six halfedges, and 2 faces (the triangle and the unbounded face). The list of vertices each represented by its associated point follows, as shown in the output example. The next list is the one of halfedges, each component is represented by its index (0,1 or 2) in the vertices list and its associated segment. The faces list is presented next. It starts with the unbounded face having one hole which is the triangle, this connected component specifies that the hole has three halfedges with the indices 4, 0 and 3. The next face presenting the triangle is written in the same manner.
# ------------------------------------- Printing Planar map # -------------------------------------------------------- # Printing number of vertices halfedges and faces in Planar map 3 6 2 # 3 vertices # ------------------------------------------ 1/1 1/1 0/1 0/1 2/1 0/1 # 6 halfedges # ------------------------------------------ 0 0/1 0/1 1/1 1/1 1 0/1 0/1 1/1 1/1 0 1/1 1/1 2/1 0/1 2 1/1 1/1 2/1 0/1 1 2/1 0/1 0/1 0/1 2 2/1 0/1 0/1 0/1 # 2 faces # ------------------------------------------ # writing face # ------------------------------------------ # UNBOUNDED # number halfedges on outer boundary 0 # number of holes 1 # inner ccb # number halfedges on inner boundary 3 4 0 3 # finish writing face # ------------------------------------------ # writing face # ------------------------------------------ # outer ccb # number halfedges on outer boundary 3 5 2 1 # number of holes 0 # finish writing face # ------------------------------------------ # ------------------------------------- End of Planar map # --------------------------------------------------------
The following program demonstrates the usage of I/O functions while users have an additional attribute in their planar map. The attribute chosen here is adding an associative color to each vertex. First the program extends the Dcel to maintain this attribute. Second, the program extends the Pm_file_writer class to handle the newly defined vertex. It simply overrides the functions for writing a vertex to print the color of the vertex as well. Finally, the main function defines an empty Planar map, reads it from the standard input stream, and then set all vertices colors. It then defines an object of its extended writer class and parameterize the function write_pm with that object.
// file: examples/Planar_map/example10.C #include <CGAL/Cartesian.h> #include <CGAL/Quotient.h> #include <CGAL/Pm_default_dcel.h> #include <CGAL/Planar_map_2.h> #include <CGAL/Pm_segment_traits_2.h> #include <CGAL/IO/Pm_iostream.h> #include <CGAL/IO/write_pm.h> #include <iostream> #include <string> template <class Pt> class Pm_my_vertex : public CGAL::Pm_vertex_base<Pt> { public: Pm_my_vertex() : CGAL::Pm_vertex_base<Pt>() { } void set_color(const std::string & c) { color = c; } std::string get_color() const { return color;} private: std::string color; }; // building new dcel with my vertex base. template <class Traits> class Pm_my_dcel : public CGAL::Pm_dcel<Pm_my_vertex<typename Traits::Point_2>, CGAL::Pm_halfedge_base<typename Traits::X_monotone_curve_2>, CGAL::Pm_face_base> { public: // Creation Pm_my_dcel() { } }; // extend the drawer to print the color as well. template <class PM> class Pm_my_file_writer : public CGAL::Pm_file_writer<PM> { public: typedef typename PM::Vertex_handle Vertex_handle; typedef typename PM::Vertex_const_handle Vertex_const_handle; typedef typename PM::Vertex_iterator Vertex_iterator; typedef typename PM::Vertex_const_iterator Vertex_const_iterator; Pm_my_file_writer(std::ostream & o, const PM & pm, bool verbose = false) : CGAL::Pm_file_writer<PM>(o, pm, verbose) { } void write_vertex(Vertex_const_handle v) const { this->out() << v->point() <<" "; this->out() << v->get_color()<< std::endl; } }; typedef CGAL::Quotient<int> NT; typedef CGAL::Cartesian<NT> Kernel; typedef CGAL::Pm_segment_traits_2<Kernel> Traits; typedef Pm_my_dcel<Traits> Dcel; typedef CGAL::Planar_map_2<Dcel,Traits> Planar_map; typedef Planar_map::Vertex_iterator Vertex_iterator; int main() { Planar_map pm; std::cin >> pm; std::cout << "* * * Demonstrating definition of user attributes for " << "Planar map components" << std::endl << std::endl << std::endl; // Update the colors for halfedge and vertex: for (Vertex_iterator v_iter = pm.vertices_begin(); v_iter != pm.vertices_end(); ++v_iter) v_iter->set_color("BLUE"); // Print the map to output stream with the user attributes: std::cout << "* * * Printing the Planar map" << std::endl; std::cout << std::endl; Pm_my_file_writer<Planar_map> writer(std::cout, pm); CGAL::write_pm(pm, writer, std::cout); return 0; }
The input of the program is a text file presenting the Planar map:
# ------------------------------------- Printing Planar map # -------------------------------------------------------- # Printing number of vertices halfedges and faces in Planar map 3 6 2 # 3 vertices # ------------------------------------------ 1/1 1/1 0/1 0/1 2/1 0/1 # 6 halfedges # ------------------------------------------ 0 0/1 0/1 1/1 1/1 1 0/1 0/1 1/1 1/1 0 1/1 1/1 2/1 0/1 2 1/1 1/1 2/1 0/1 1 2/1 0/1 0/1 0/1 2 2/1 0/1 0/1 0/1 # 2 faces # ------------------------------------------ # writing face # ------------------------------------------ # UNBOUNDED # number halfedges on outer boundary 0 # number of holes 1 # inner ccb # number halfedges on inner boundary 3 4 0 3 # finish writing face # ------------------------------------------ # writing face # ------------------------------------------ # outer ccb # number halfedges on outer boundary 3 5 2 1 # number of holes 0 # finish writing face # ------------------------------------------ # ------------------------------------- End of Planar map # --------------------------------------------------------
The output is the Planar map written in both formats, non verbose and verbose. In addition the two lists (non verbose and verbose) of halfedges are written.
* * * Demonstrating definition of user attributes for Planar map components * * * Printing the Planar map # ------------------------------------- Begin Planar Map # -------------------------------------------------------- # Number of vertices halfedges and faces in Planar map 3 6 2 # 3 vertices # ------------------------------------------ 1/1 1/1 BLUE 0/1 0/1 BLUE 2/1 0/1 BLUE # 6 halfedges # ------------------------------------------ 0 0/1 0/1 1/1 1/1 1 0/1 0/1 1/1 1/1 0 1/1 1/1 2/1 0/1 2 1/1 1/1 2/1 0/1 1 2/1 0/1 0/1 0/1 2 2/1 0/1 0/1 0/1 # 2 faces # ------------------------------------------ # writing face # ------------------------------------------ # UNBOUNDED # number halfedges on outer boundary 0 # number of holes 1 # inner ccb # number halfedges on inner boundary 3 4 0 3 # finish writing face # ------------------------------------------ # writing face # ------------------------------------------ # outer ccb # number halfedges on outer boundary 3 5 2 1 # number of holes 0 # finish writing face # ------------------------------------------ # ------------------------------------- End Planar Map # --------------------------------------------------------
More details are given in sections File_header, Pm_file_scanner<Planar_map>, Pm_file_writer<Planar_map> and Pm_drawer<Planar_map>.
| advanced |
|
We supply a default traits class for segments, namely Pm_segment_traits_2<Kernel>, where Kernel is a kernel representation type, e.g., Homogeneous or Cartesian. This traits class handles finite line segments in the plane. In this class the X_monotone_curve_2 and Point_2 types are defined as the CGAL kernel types Kernel::Segment_2 and Kernel::Point_2 respectively, and the CGAL kernel operations on these types are exploited to implement the required functions. The leda_rat_kernel_traits class exploits LEDA's rational kernel and its efficient predicates. As a model that conforms to the CGAL kernel concept, it can be injected to the Pm_segment_traits_2<Kernel> class. leda_rat_kernel_traits class is available as an external package.
Models of PlanarMapTraits_2 are meant to serve as arguments for the respective template parameter of CGAL::Planar_map_2<Dcel,Traits>. However, it should be noted that each model of PlanarMapTraits_2 defines a family of curves and primitive geometric operations thereof. Sometimes, the only implementation available for the manipulation of a certain family of curves is one of the supplied traits classes. A scenario where one uses a traits class object to manipulate such curves without maintaining planar maps is certainly possible.
ArrangementTraits_2 concept is a refinements of the
PlanarMapWithIntersectionsTraits_2 concept, and the latter is a
refinement of the PlanarMapTraits_2 concept.
Therefore, all models of the formers are models of the latter.
There are several supplied traits classes for the Arrangement
that you can use. These classes are described at the end of Chapter
(2D Arrangements).
The class has a point location function (namely, the locate function that determines which feature of the map contains a given query point) which is also used internally in the insert function. You can define which algorithm to use in the point location queries. This is done with a point location class passed to the map in the constructor. The class passed should be derived from the base class Pm_point_location_base which is a (pure virtual) base class that defines the interface between the algorithm implemented by the users and the planar map. This follows the known Strategy pattern [GHJV95]. The indirection overhead due to the virtual functions is negligible since the optimal point location algorithm (e.g., the one implemented in our default strategy) takes log time. We have derived three concrete classes for point location strategies, the trapezoid-randomized-incremental-construction strategy, based on a trapezoidal decomposition of the map, the naive strategy, which goes over all the vertices and halfedges of the planar map and the walk-along-a-line strategy, which improves the naive one by ``walking'' only along the zone of the vertical ray emanating from the query point. All three strategies are classes that inherit Pm_point_location_base<Planar_map>. More details are give in sections Pm_trapezoid_ric_point_location<Planar_map>, Pm_naive_point_location<Planar_map> and Pm_walk_along_a_line_point_location<Planar_map>.
Trade-off Issues
The main trade-off among the three strategies implemented, is between time and storage. Using the naive or walk strategies takes more time but saves storage space.
Another trade-off depends on the need for point location queries compared to the need for other functions. If you do not need point location queries, but do need other modifying functions (e.g., remove_edge, split_edge and merge_edge) then using the naive or walk strategies is preferable. Note that using the insert function invokes the point location query, therefore when using the naive or walk strategies it is recommended to use the specialized insertion functions : insert_in_face_interior, insert_from_vertex and insert_at_vertices. For example, when using the planar map to represent polygons (e.g., when computing boolean operations on polygons) it might be preferable to use the walk strategy with the specialized insertion functions.
There are two modes of the default strategy which enables you to choose whether preprocessing should be performed or not (read more in the section stated above). There is a trade-off between those two modes. If preprocessing is not used, the building of the structure is faster. However, for some input sequences the structure might be unbalanced and therefore queries and updates might take longer, especially, if many removal and split operation are performed.
Before we list specific tips, we remind you that compiling programs with debug flags turned off, and with optimization flags turned on, significantly reduces running time.
Insertion of a polygon, which is represented by a list of segments along its boundary, into an empty planar map should be done in the following way. First, some segment should be inserted using insert_in_face_interior with the unbounded face. Then a segment with a common end point can be inserted using insert_from_vertex and so on with the rest of the segments but last. The last segment can be inserted using insert_at_vertices since both it endpoints are represented as vertices of the map and are known in advanced.
The following program demonstrates the use of I/O functions provided for planar maps. First the program demonstrates a trivial use of the I/O functions: it defines an empty instance of Planar_map_2, reads the planar map representation text from the standard input stream, and then prints the resulting planar map to the standard output stream.
Second, it presents the usage of the verbose format, by defining Pm_file_writer with the verbose flag set to true, and then calls the function write_pm. A usage of the interface of the class Pm_file_writer is also presented, by calling its function write_halfedges, which prints all the halfedges of the map. In addition, the program presents the operators writing the resulting Planar map to a postscript file when LEDA is installed. The demo for the planar map package makes use of the output operator of Planar_map_2<Dcel,Traits> to a window stream (see at <CGAL_ROOT>/demo/Planar_map/demo.C ).
// file: examples/Planar_map/example9.C
#include "short_names.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Planar_map_2.h>
#include <CGAL/Pm_segment_traits_2.h>
#include <CGAL/IO/write_pm.h>
#include <CGAL/IO/Pm_iostream.h>
#include <iostream>
// #define CGAL_POSTSCRIPT
#if defined(CGAL_USE_LEDA) && defined(CGAL_POSTSCRIPT)
#include <CGAL/IO/Pm_Postscript_file_stream.h>
#endif
typedef CGAL::Quotient<int> NT;
typedef CGAL::Cartesian<NT> Kernel;
typedef CGAL::Pm_segment_traits_2<Kernel> Traits;
typedef CGAL::Pm_default_dcel<Traits> Dcel;
typedef CGAL::Planar_map_2<Dcel,Traits> Planar_map;
typedef CGAL::Pm_file_writer<Planar_map> Pm_writer;
int main()
{
Planar_map pm;
Pm_writer verbose_writer(std::cout, pm, true);
Pm_writer writer(std::cout, pm);
std::cout << "* * * Demonstrating a trivial use of IO functions"
<< std::endl << std::endl;
std::cin >> pm;
std::cout << pm;
std::cout << std::endl;
std::cout << "* * * Presenting the use of verbose format" << std::endl;
std::cout << std::endl;
CGAL::write_pm(pm, verbose_writer, std::cout);
std::cout << std::endl;
std::cout << "* * * Demonstrating the use of the writer class interface."
<< std::endl;
std::cout << "* * * Printing all halfedges in non verbose format"
<< std::endl << std::endl;
writer.write_halfedges(pm.halfedges_begin(), pm.halfedges_end());
std::cout << std::endl;
std::cout << "* * * Printing all halfedges in a verbose format" << std::endl
<< std::endl;
verbose_writer.write_halfedges(pm.halfedges_begin(), pm.halfedges_end());
#if defined(CGAL_USE_LEDA) && defined(CGAL_POSTSCRIPT)
// Print to Postscript file:
CGAL::Postscript_file_stream LPF(500, 500 ,"pm.ps");
LPF.init(-3,3,-3);
LPF.set_line_width(1);
LPF << pm;
#endif
return 0;
}
The input of the program is a text file which holds the planar map representation in a special format (which is presented in the reference pages of the the Planar Map package. This representation appears as the first block in the output file.
The output is the Planar map includes both formats, non-verbose and verbose. In addition the two lists (non-verbose and verbose) of halfedges are written.
* * * Demonstrating a trivial use of IO functions # ------------------------------------- Begin Planar Map # -------------------------------------------------------- # Number of vertices halfedges and faces in Planar map 3 6 2 # 3 vertices # ------------------------------------------ 1/1 1/1 0/1 0/1 2/1 0/1 # 6 halfedges # ------------------------------------------ 0 0/1 0/1 1/1 1/1 1 0/1 0/1 1/1 1/1 0 1/1 1/1 2/1 0/1 2 1/1 1/1 2/1 0/1 1 2/1 0/1 0/1 0/1 2 2/1 0/1 0/1 0/1 # 2 faces # ------------------------------------------ # writing face # ------------------------------------------ # UNBOUNDED # number halfedges on outer boundary 0 # number of holes 1 # inner ccb # number halfedges on inner boundary 3 4 0 3 # finish writing face # ------------------------------------------ # writing face # ------------------------------------------ # outer ccb # number halfedges on outer boundary 3 5 2 1 # number of holes 0 # finish writing face # ------------------------------------------ # ------------------------------------- End Planar Map # -------------------------------------------------------- * * * Presenting the use of verbose format # ------------------------------------- Begin Planar Map # -------------------------------------------------------- # Number of vertices halfedges and faces in Planar map 3 6 2 # 3 vertices # ------------------------------------------ 1/1 1/1 0/1 0/1 2/1 0/1 # 6 halfedges # ------------------------------------------ 0/1 0/1 1/1 1/1 towards 1/1 1/1 0/1 0/1 1/1 1/1 towards 0/1 0/1 1/1 1/1 2/1 0/1 towards 1/1 1/1 1/1 1/1 2/1 0/1 towards 2/1 0/1 2/1 0/1 0/1 0/1 towards 0/1 0/1 2/1 0/1 0/1 0/1 towards 2/1 0/1 # 2 faces # ------------------------------------------ # writing face # ------------------------------------------ # UNBOUNDED # number halfedges on outer boundary 0 # number of holes 1 # inner ccb # number halfedges on inner boundary 3 2/1 0/1 0/1 0/1 towards 0/1 0/1 0/1 0/1 1/1 1/1 towards 1/1 1/1 1/1 1/1 2/1 0/1 towards 2/1 0/1 # finish writing face # ------------------------------------------ # writing face # ------------------------------------------ # outer ccb # number halfedges on outer boundary 3 2/1 0/1 0/1 0/1 towards 2/1 0/1 1/1 1/1 2/1 0/1 towards 1/1 1/1 0/1 0/1 1/1 1/1 towards 0/1 0/1 # number of holes 0 # finish writing face # ------------------------------------------ # ------------------------------------- End Planar Map # -------------------------------------------------------- * * * Demonstrating the use of the writer class interface. * * * Printing all halfedges in non verbose format 0 0/1 0/1 1/1 1/1 1 0/1 0/1 1/1 1/1 0 1/1 1/1 2/1 0/1 2 1/1 1/1 2/1 0/1 1 2/1 0/1 0/1 0/1 2 2/1 0/1 0/1 0/1 * * * Printing all halfedges in a verbose format 0/1 0/1 1/1 1/1 towards 1/1 1/1 0/1 0/1 1/1 1/1 towards 0/1 0/1 1/1 1/1 2/1 0/1 towards 1/1 1/1 1/1 1/1 2/1 0/1 towards 2/1 0/1 2/1 0/1 0/1 0/1 towards 0/1 0/1 2/1 0/1 0/1 0/1 towards 2/1 0/1
| 1 | A conic section is the nondegenerate curve generated by the intersections of a plane with one or two nappes of a cone. |