Navigation: Up, Table of Contents, Bibliography, Index, Title Page

Chapter 23
2D Arrangements

Ester Ezra, Eyal Flato, Dan Halperin, Iddo Hanniel, Shai Hirsch, and Ron Wein

23.1   Introduction

Given a collection of (possibly intersecting and not necessarily x-monotone) curves in the plane, the planar arrangement of is the subdivision the curves of induce on the plane into zero-dimensional, one-dimensional and two-dimensional cells, called vertices, edges and faces respectively.

23.2   Software Design

The class Arrangement_2<Dcel,Traits,Base_node> is a data structure for maintaining 2D arrangements. The data structure maintains a planar map and curve hierarchy trees. There is a curve tree for each curve inserted into the arrangement (see below). The underlying combinatorial structure is determined by the Dcel template parameter, which should be a model of the ArrangementDcel_2 concept. The family of curves of the arrangement is determined by the Traits template parameter which should be a model of the ArrangementTraits_2 concept. The Base_node template parameter defines the attributes associated with each tree node of the hierarchy tree.

The Arrangement package is based on the Planar Map with Intersections package (see Chapter reference). That is, given a collection , we construct a collection '' in two steps: First we decompose each curve in into maximal x-monotone curves, thus obtaining the collection '. We then decompose each curve in ' into maximal connected pieces not intersecting any other curve in '. This way we obtain the collection '' of x-monotone, pairwise interior-disjoint curves. The arrangement of the curves in C is the planar map (see Chapter reference) induced by the curves in C''.

Curve Hierarchy Tree: When constructing the arrangement of a collection of curves , we decompose each curve c in two steps: First we decompose it into maximal x-monotone curves, thus obtaining a set of curves C'. We then decompose each curve in C' into maximal connected pieces not intersecting any other curve in , obtaining the set C''.

We regard these sets C', C'' as levels in a hierarchy of curves where the union of the subcurves in each level is the original curve c. We store these sets in a special structure - a hierarchy tree. This structure usually consists of three levels, although in some cases they can consist of less (e.g., when inserting an x-monotone curve) or more (when the users define their own split functions see Section reference). The levels are:

Figure reference shows an example of a simple arrangement and its corresponding curve hierarchy.

Figure:  A simple arrangement of two polylines, and its corresponding hierarchy tree (the edges of the arrangement are numbered according to their order in the tree).

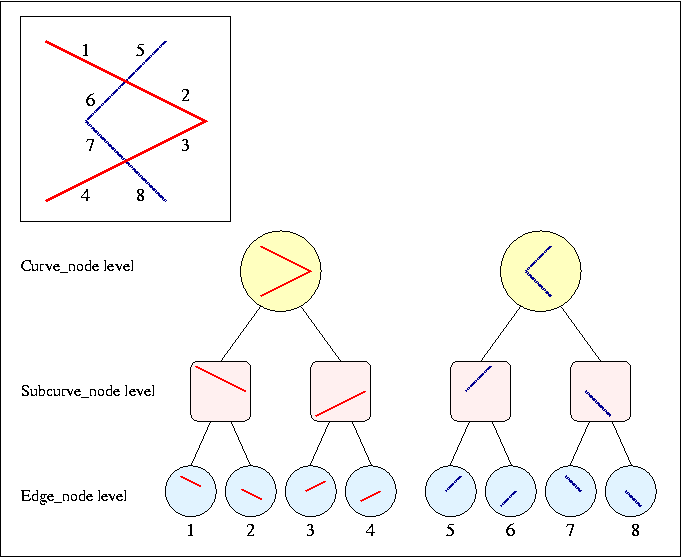
The hierarchy tree enables us to intersect the curves without loss of information. The original curve and the intermediate subcurves are stored in the tree and the user can traverse them. Furthermore, users can define their own hierarchy by passing their own intersection sequence. This can be of use in some applications. For example, in an arrangement of spline curves the users might want to intersect a curve in the junction points before making the curve x-monotone.

Degeneracies Like the planar map package (see Chapter reference), the arrangement package can deal with x-degenerate input (including vertical segments). However, while in the planar map the input curves were assumed to be x-monotone and non-intersecting in their interiors, there are no such assumptions in the arrangement. A non x-monotone curve is partitioned into x-monotone subcurves, and curves are intersected in their points of intersection with other points before they are inserted into the map. Furthermore, overlapping curves are supported. If two curves overlap the traits intersection function returns the two endpoints of the common part. Circulators of the Overlap_circulator type (of Arrangement_2<Dcel,Traits,Base_node>) enables to traverse all overlapping edge_nodes that correspond to the same pair of halfedges in the map.

I/O functions: I/O functions for reading a saved arrangement from the standard input, writing it to the standard output or drawing it to a graphic stream are also provided. Users of I/O functions for the arrangement package are required to define I/O operators for the curves defined in their Traits classes.

Update Mode: For some algorithms, it is not necessary to build the whole planar map induced by the arrangement. For example, the lower envelope of an arrangement of x-monotone curves that intersect each other at most a fixed constant number of s times, can be found in near linear time [SA95, Hal97] even if the complexity of the planar map induced by it is quadratic. Therefore, building the planar map induced by the arrangement is not always desired. The users can therefore disable (or postpone) the building of the planar map. This is done by disabling the update mode using the set_update(bool) member function. When update mode is set to true, the planar map is updated - this is the default situation. When update mode is set to false, the hierarchy tree is built without its Edge_level, and the curves are not inserted into the planar map.

23.3   Segment Arrangements

The second template parameter of the arrangement class determines the so-called geometry of the arrangement, that is the family of curves we want to deal with. In order to deal with line segments we simply plug in on of the two segment traits classes supplied.

The Arr_segment_traits_2<Kernel> class is generic and allows flexibility in determining the kernel which is used. It makes intensive use of the kernel, since it support almost all the operations needed by the arrangement package. The Arr_segment_cached_traits_2<Kernel> class stores some additional cached information with each segment curve. Choosing to work with this traits class means a little extra memory consumption, however it usually speeds up the construction time of the arrangement.

23.3.1   Example of an Arrangement of Segments

The following example demonstrates the construction of an X-shaped arrangement out of two segments. After the construction we traverse the edges of the arrangement in the order defined by the original segments.

The four numbers on each output lines is a representation of a segment. The first two numbers are the x and y coordinates of the first endpoint. The other two numbers are of the second endpoint. The way a curve is printed depends on the the output operator implemented for it. 

// file: examples/Arrangement_2/example1.C

#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits;

typedef Traits::Point_2                                 Point_2;
typedef Traits::Curve_2                                 Curve_2;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;

typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr_2;

int main() 
{
  Arr_2 arr;

  //insertion of the curves
  arr.insert(Curve_2(Point_2(0, 0), Point_2(1, 1)));
  arr.insert(Curve_2(Point_2(0, 1), Point_2(1, 0))); 
  
  //traversal of the curves
  Arr_2::Curve_iterator cit;
  Arr_2::Edge_iterator eit;
  for (cit = arr.curve_node_begin(); cit != arr.curve_node_end(); ++cit) 
  {
    std::cout << std::endl << "Curve level:" << std::endl << cit->curve()
              << std::endl ;
    std::cout << "Edge level:" << std::endl;

    //traversal of the edges of the current curve
    for (eit = cit->edges_begin(); eit != cit->edges_end(); ++eit) 
    {
      std::cout << eit->x_curve() << std::endl ;
    }
  }

  return 0;
}

The output of the program looks like this: 

Curve level:
0 0 1 1
Edge level:
0 0 0.5 0.5
0.5 0.5 1 1

Curve level:
0 1 1 0
Edge level:
0 1 0.5 0.5
0.5 0.5 1 0

23.3.2   Example of Overlapping Segments

The following example demonstrates the construction of an arrangement out of two overlapping segments - (0,0)-(2,2) and (1,1)-(3,3). After the insertion of the segments we traverse the halfedges of the arrangement and count the overlapping curves. This is done using the overlap_edges() member function that returns an Overlap_circulator. With it we can circulate over all the edge nodes that correspond to the halfedge. 

// file: examples/Arrangement_2/example2.C

#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/circulator.h>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits;
typedef Traits::Point_2                                 Point_2;
typedef Traits::Curve_2                                 Curve_2;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;
typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr_2;

int main() 
{
  Arr_2 arr;

  // Insertion of the curves
  arr.insert(Curve_2(Point_2(0, 0), Point_2(2, 2)));
  arr.insert(Curve_2(Point_2(1, 1), Point_2(3, 3)));

  // Traversal of the halfedges
  Arr_2::Halfedge_const_iterator hit = arr.halfedges_begin(),
      hit_end = arr.halfedges_end();

  for (; hit != hit_end; ++hit, ++hit)
  {
    // We skip the adjacent twin halfedge
    Arr_2::Overlap_const_circulator occ = hit->overlap_edges(), occ_end = occ;
    int count = 0;
    CGAL_For_all(occ, occ_end) { ++count; }

    if (count == 1) 
      std::cout << "Edge " << occ->x_curve() << " is covered by a single edge."
                << std::endl;
    else
      std::cout << "Edge " << occ->x_curve() << " is covered by " << count
                << " edges." << std::endl;
  }

  return 0;
}

The output of the program looks like this: 

Edge 0 0 1 1 is covered by a single edge.
Edge 1 1 2 2 is covered by 2 edges.
Edge 2 2 3 3 is covered by a single edge.

23.4   Polyline Arrangements

The Arr_polyline_traits_2<Segment_traits> class can be used to handle arrangements of polylines (a.k.a. poly-segment). A polyline can be created from any range of points, where the ith and (i+1)st points in the range represent the endpoints of the ith segment of the polyline. The polyline traits class is templated with another traits class that supports the basic operations on segments.

23.4.1   Example of a Polyline Arrangement

The following example demonstrates the use of the polyline traits. Observe that a polyline curve is constructed from a standard STL vector of points.

Note that a polyline point is not necessarily a vertex of the arrangement (that is, of the underlying Planar Map) and an edge of the Planar Map need not be a segment. The edges are only required to be x-monotone and pairwise disjoint. In the example below point (150, 50) is not a vertex of the planar map. The polyline to which it belongs is an edge of the planar map.

However, one might expect the planar map (or rather the edge level of the arrangement) to be made of segments alone. In such cases the user can define additional level of hierarchies, as will be shown in the example in Section reference. 

// file: examples/Arrangement_2/example10.C

// Define shorter names to please linker (g++)
#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_polyline_traits_2.h>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Seg_traits;
typedef CGAL::Arr_polyline_traits_2<Seg_traits>         Traits;

typedef Traits::Point_2                                 Point_2;
typedef Traits::Curve_2                                 Curve_2;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;

typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr_2;

int main()
{
  Arr_2                arr;
  std::vector<Point_2> pts;

  // Curve #1, not x monotone.
  pts.push_back(Point_2(  0,  0));
  pts.push_back(Point_2( 10, 10));
  pts.push_back(Point_2(  0, 20));
  arr.insert (Curve_2(pts.begin(), pts.end())); 
  
  // Curve #2, x monotone.
  pts.clear();
  pts.push_back(Point_2(100,  0));
  pts.push_back(Point_2(150, 50));
  pts.push_back(Point_2(200,  0));
  arr.insert (Curve_2(pts.begin(), pts.end()));

  // Curve #1 is broken into two edges. Point_2 (10,10) turns into a vertex.
  Arr_2::Locate_type lt;
  arr.locate(Point_2(10, 10), lt);
  CGAL_assertion(lt == Arr_2::VERTEX);

  return 0;
}

23.5   Arrangements of Conic Arcs

The Arr_conic_traits_2<Int_kernel, Alg_kernel> class can be used for constructing arrangement of bounded segments of algebraic curves of degree 2 (conic curves). That is, it supports the construction of the arrangement of any collection of elliptic arcs (a full ellipse or a circle may also be considered as a conic arc), hyperbolic arcs, parabolic arcs and also line segments. The template has two template parameters:

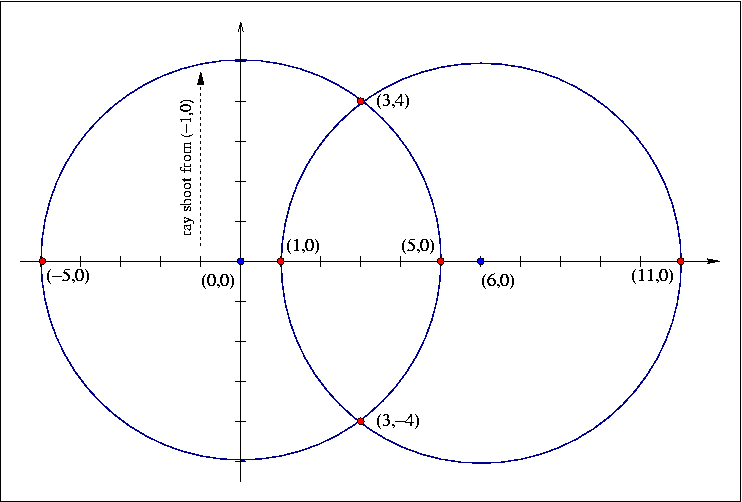
23.5.1   Example of an Arrangement of Circular Arcs

The following example demonstrates the use of the conic traits for constructing a simple arrangement of two circles. The arrangement created by this example is depicted in Figure reference. Note that each circle is divided to an upper half and a lower half, both are x-monotone: The result of ray-shooting operation from (-1,0) upward exemplifies this, since it returns a circular arcs whose end-points are (3,4) and (-5,0).

Figure:  The arrangement generated by the example program. 

// file: examples/Arrangement_2/example3.C   

#include "short_names.h"

#include <CGAL/basic.h>

#ifndef CGAL_USE_CORE
// To enable compilation without core:
int main ()
{
  return (0);
}

#else

#include <CGAL/Cartesian.h>
#include <CORE/BigInt.h>
#include <CGAL/CORE_Expr.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_conic_traits_2.h> 
#include <CGAL/Arrangement_2.h>

typedef CORE::BigInt                                CfNT;
typedef CGAL::Cartesian<CfNT>                       Int_kernel;
typedef Int_kernel::Point_2                         Int_point_2;
typedef Int_kernel::Circle_2                        Int_circle_2;

typedef CORE::Expr                                      CoNT;
typedef CGAL::Cartesian<CoNT>                           Alg_kernel;

typedef CGAL::Arr_conic_traits_2<Int_kernel,Alg_kernel> Traits_2;
typedef Traits_2::Point_2                               Point_2;
typedef Traits_2::Curve_2                               Curve_2;
typedef Traits_2::X_monotone_curve_2                    X_monotone_curve_2;
typedef CGAL::Arr_2_default_dcel<Traits_2>              Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits_2>              Arr_2;

int main()
{
  Arr_2 arr;  
              
  // 2 ccw circles with radius 5 and center (0,0) and (6,0) resp.
  Int_circle_2  c1 (Int_point_2(0,0), 5*5);
  Int_circle_2  c2 (Int_point_2(6,0), 5*5);

  Arr_2::Curve_iterator cit = arr.insert(Curve_2 (c1));
  cit = arr.insert(Curve_2 (c2)); 

  // upward vertical ray shooting
  Arr_2::Locate_type lt;
  Arr_2::Halfedge_handle e = arr.vertical_ray_shoot(Point_2(-1, 0), lt, true);

  CGAL_assertion(e->source()->point() == Point_2(3, 4)); 
  CGAL_assertion(e->target()->point() == Point_2(-5, 0));

  return 0;
}

#endif

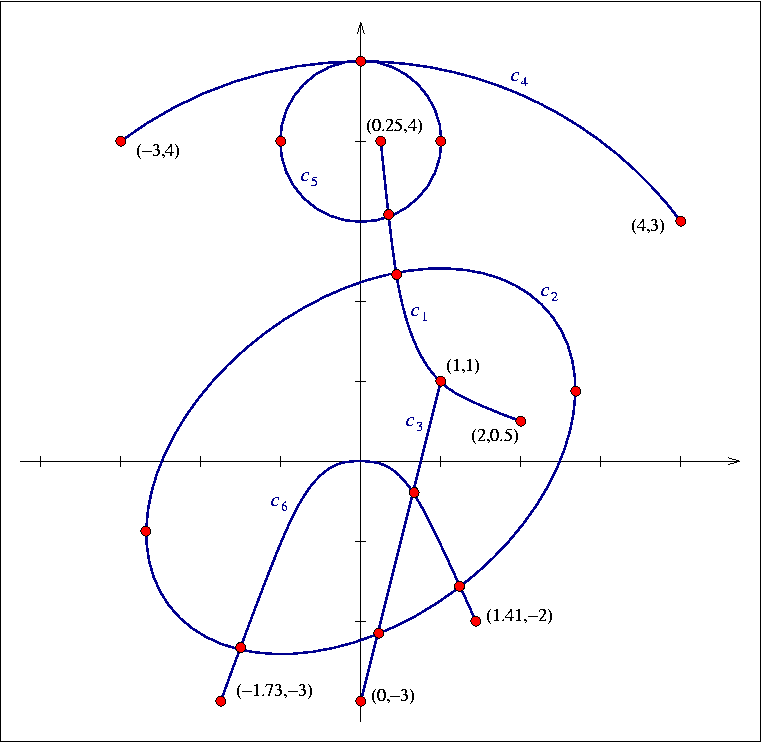
23.5.2   Example of an Arrangement of Mixed Conic Arcs

The following example demonstrates the construction of an arrangement of various conic arcs of mixed types. The input Curve_2 objects are created in a way that makes use of most available constructors for conic arcs.

The arrangement created by this example is depicted in Figure reference. The program outputs the number of vertices, edges and faces in the resulting arrangement, and the correctness of these figures can be easily verified by counting them in this figure: Notice that arrangement vertices may be original endpoints of the input curves, intersection points of two (or more) curves or points where the tangent to the curve is a vertical line.

Figure:  The arrangement of conic arcs generated by the example program. The coordinates of the input endpoints are also shown. 

// file: examples/Arrangement_2/example3.C

#include "short_names.h"

#ifndef CGAL_USE_CORE
// To enable compilation without core:
int main ()
{
  return (0);
}

#else

#include <CGAL/basic.h>
#include <CGAL/Cartesian.h>
#include <CORE/BigInt.h>
#include <CGAL/CORE_Expr.h>
#include <CGAL/Arr_2_bases.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_conic_traits_2.h> 
#include <CGAL/Arrangement_2.h>

typedef CORE::BigInt                                CfNT;
typedef CGAL::Cartesian<CfNT>                       Int_kernel;
typedef Int_kernel::Point_2                         Int_point_2;
typedef Int_kernel::Segment_2                       Int_segment_2;
typedef Int_kernel::Line_2                          Int_line_2;
typedef Int_kernel::Circle_2                        Int_circle_2;

typedef CORE::Expr                                      CoNT;
typedef CGAL::Cartesian<CoNT>                           Alg_kernel;

typedef CGAL::Arr_conic_traits_2<Int_kernel,Alg_kernel>  Traits_2;
typedef Traits_2::Point_2                                Point_2;
typedef Traits_2::Curve_2                                Curve_2;
typedef Traits_2::X_monotone_curve_2                     X_monotone_curve_2;
typedef CGAL::Arr_base_node<Curve_2, X_monotone_curve_2> Base_node;
typedef CGAL::Arr_2_default_dcel<Traits_2>               Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits_2,Base_node>     Arr_2;

int main()
{
  Arr_2 arr;  
             
  // Insert a hyperbolic arc, supported by the hyperbola y = 1/x
  // (or: xy - 1 = 0) with the end-points (0.25, 4) and (2, 0.5).
  // Note that the arc is counterclockwise oriented.
  Point_2   ps1 (0.25, 4);
  Point_2   pt1 (2, 0.5);
  Curve_2   c1 (0, 0, 1, 0, 0, -1, CGAL::COUNTERCLOCKWISE, ps1, pt1);

  arr.insert(c1);

  // Insert a full ellipse, which is (x/4)^2 + (y/2)^2 = 0 rotated by
  // phi=36.87 degree (such that sin(phi) = 0.6, cos(phi) = 0.8),
  // yielding: 58x^2 + 72y^2 - 48xy - 360 = 0.
  Curve_2   c2 (58, 72, -48, 0, 0, -360);
  
  arr.insert(c2);

  // Insert the segment (1, 1) -- (0, -3).
  Int_point_2   ps3 (1, 1);
  Int_point_2   pt3 (0, -3);
  Curve_2       c3 (Int_segment_2 (ps3, pt3));

  arr.insert(c3);

  // Insert a circular arc supported by the circle x^2 + y^2 = 5^2,
  // with (-3, 4) and (4, 3) as its endpoints. We want the arc to be
  // clockwise oriented, so it passes through (0, 5) as well.
  Int_point_2   ps4 (-3, 4);
  Int_point_2   pm4 (0, 5);
  Int_point_2   pt4 (4, 3);
  Curve_2       c4 (ps4, pm4, pt4);

  arr.insert(c4);

  // Insert a full unit circle that is centered at (0, 4).
  Int_circle_2  circ5 (Int_point_2(0,4), CfNT(1));
  Curve_2   c5 (circ5);
  
  arr.insert(c5);

  // Insert a parabolic arc that is supported by a parabola y = -x^2
  // (or: x^2 + y = 0) and whose end-points are (-sqrt(3), -3) ~ (-1.73, -3)
  // and (sqrt(2), -2) ~ (1.41, -2). Notice that since the x-coordinates 
  // of the end-points cannot be acccurately represented, we specify them
  // as the intersections of the parabola with the lines y = -3 and y = -2.
  // Note that the arc is clockwise oriented.
  Curve_2   c6 (1, 0, 0, 0, 1, 0,       // The parabola.
		CGAL::CLOCKWISE,
		Point_2 (-1.73, -3),    // Approximation of the source.
		0, 0, 0, 0, 1, 3,       // The line: y = -3.
		Point_2 (1.41, -2),     // Approximation of the target.
		0, 0, 0, 0, 1, 2);      // The line: y = -2.

  arr.insert(c6);

  // Print out the number of vertices, edges and faces in the arrangement.
  std::cout << "Number of vertices: " 
	    << arr.number_of_vertices() << std::endl;
  
  std::cout << "Number of edges: " 
	    << arr.number_of_halfedges()/2 << std::endl;
  std::cout << "Number of faces: " 
	    << arr.number_of_faces() << std::endl;

  return 0;
}

#endif

The output of the program looks like this: 

Number of vertices: 19
Number of edges: 23
Number of faces: 6


begin of advanced section  advanced  begin of advanced section

23.6   User-defined Hierarchy

The default hierarchy structure can be extended to include more levels according to user defined split functions.

23.6.1   Example of a User-defined Hierarchy

The following example demonstrates the construction of an arrangement of two segments, using a user-defined hierarchy. We use a simple split function that splits a segment in its middle point. We insert the first segment using the user-defined function and the second segment with the regular function. 

// file: examples/Arrangement_2/example4.C

#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <vector>
#include <list>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits;
typedef Traits::Point_2                                 Point_2;
typedef Traits::Curve_2                                 Curve_2;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;
typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr_2;

// A simple function that splits a segment into 2
void my_split_f(const Curve_2 & cv, std::list<Curve_2> & l) 
{
  Point_2 s = cv.source(); // Uses the knowledge of the curve functions
  Point_2 t = cv.target();
  Point_2 m1 = s + (t - s) / 2.0;
  l.push_back(Curve_2(s, m1));
  l.push_back(Curve_2(m1, t));
}

typedef void (*SPLIT_FUNC)(const Curve_2 & cv, std::list<Curve_2> & l);

int main() 
{
  std::vector<SPLIT_FUNC> func_vec;
  func_vec.push_back(&my_split_f);
  Arr_2 arr;
   
  // Insertion with user-defined function
  Arr_2::Curve_iterator cit = arr.insert(Curve_2(Point_2(0, 0),Point_2(6, 6)),
                                         func_vec.begin(), func_vec.end());
   
  // Regular insertion                                  
  cit = arr.insert(Curve_2(Point_2(0, 4), Point_2(6, 4))); 
   
  // Traversal of the curves
  Arr_2::Edge_iterator eit;
  for (cit = arr.curve_node_begin(); cit != arr.curve_node_end(); ++cit) 
  {
    std::cout << std::endl << "Curve level:" << std::endl << cit->curve()
              << std::endl ;
    std::cout << "Edge level:" << std::endl;
    for (eit = cit->edges_begin(); eit != cit->edges_end(); ++eit) 
    {
      std::cout << eit->x_curve() << std::endl ;
    }
  }

  return 0;
}

The output of the program looks like this: 

Curve level:
0 0 6 6
Edge level:
0 0 3 3
3 3 4 4
4 4 6 6

Curve level:
0 4 6 4
Edge level:
0 4 4 4
4 4 6 4

end of advanced section  advanced  end of advanced section


begin of advanced section  advanced  begin of advanced section

23.6.2   Example of a User-defined Hierarchy with Function Objects

The following example demonstrates the use of a function object in a user-defined hierarchy. We define a base class for the function objects with a virtual operator(), that the function objects override (this kind of pattern is sometimes called an Action class (see for example [Str97, Chapter 25.5]). This enables us to use an inner state in our function as is done in the example.

In the example we define two levels of a hierarchy. The first level splits the inserted segment in the middle. The second layer splits every curve of the first layer in a ratio of 1/3 : 2/3. Therefore, after an insertion of the segment (0,0) - (6,6) we will have four edges (eight halfedges) inside the arrangement, corresponding to the segments: (0,0) - (1,1), (1,1) - (3,3), (3,3) - (4,4) and (4,4) - (6,6). 

// file: examples/Arrangement_2/example5.C

#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <vector>
#include <list>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits;
typedef Traits::Point_2                                 Point;
typedef Traits::Curve_2                                 Curve;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;
typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr_2;

// A base class for split functors
struct Split_base 
{
  virtual void operator()(const Curve& cv, std::list<Curve>& l)=0;
};

// A user-defined insertion functor
struct Split_func : public Split_base 
{
  Split_func(double ratio) : r(ratio) {}
  void operator()(const Curve & cv, std::list<Curve> & l) 
  {
     Point s=cv.source(); // Uses the knowledge of the curve functions
     Point t=cv.target();
     Point m1 = s + (t - s) / r;
     l.push_back(Curve(s, m1));
     l.push_back(Curve(m1, t));

   }     

  virtual ~Split_func(){};
private:
  NT r;
};

int main() 
{
  // Prepare a vector of pointers to the functor base class 
  std::vector<Split_base*> func_vec;

  // Create 2 functors
  Split_func Sf1(2.0), Sf2(3.0);

  func_vec.push_back(&Sf1);
  func_vec.push_back(&Sf2);

  Arr_2 arr;

  // Insertion with user-defined functor
  Arr_2::Curve_iterator cit=arr.insert(Curve(Point(0, 0),Point(6, 6)),
                                       func_vec.begin(), func_vec.end());

  CGAL_assertion(arr.number_of_halfedges() == 8);
  CGAL_assertion(cit->number_of_sc_levels() == 2);

  return 0;
}

end of advanced section  advanced  end of advanced section


begin of advanced section  advanced  begin of advanced section

23.6.3   I/O functions

The Arrangement package supports I/O functions, which include reading an arrangement representation from the standard input or writing it to the standard output, and also sending an arrangement to a graphic stream.

As already mentioned at chapter , the motivation for using I/O functions is not only to be able to draw the arrangement to a window for instance, but also to be capable to save an arrangement in a text file by writing it and reloading it from a text file by reading it.

Reading an arrangement from the standard input or printing it to the standard output may be done simply with the Extractor ( >> ) and Insertor ( << ) operators defined for Arrangement_2, respectively.

#include <CGAL/IO/Arr_iostream.h>

The ability of sending the Arrangement into a graphic stream as leda_window, Postscript file or Geomview is also provided, users simply have to apply the Insertor operator on the graphic stream and their arrangement instance.

Users of I/O functions for the arrangement package are required to define I/O operators for the curves defined in their Traits classes. When using Traits classes in which this operators are already defined (as Segment Traits) the operator definition is not obligated, however using Traits classes as the Conic Traits will force the users to define I/O operators on their conic curve.

The Arrangement class data consists of the induced planar map and the obtained hierarchy tree. Hence, the data sent to the output stream or read from an input stream should contain both parts.

The format of the planar map part is as specified in the Planar Map reference pages (). The format of the hierarchy tree is specified below.

The format of the output file is defined in a way the reading function will construct the arrangement efficiently. The induced planar map is constructed efficiently as specified in the Planar Map reference pages (), and the hierarchy tree is also constructed efficiently by directly accessing its parts and updating them. When constructing an arrangement from an input stream, no use of its insertion functions is performed.

Consequently, the reading function constructs the arrangement very efficiently, and hence users who would like to save their arrangement and reload it have to construct their arrangement by the insertion functions only once. After saving the arrangement to a text file it can be reloaded very efficiently when needed, instead of constructing it from scratch.

When users would like to read their arrangement from the standard input or print it into the standard output, they may simply use the Extractor ( >> ) and Insertor ( << ) operators defined for Arrangement respectively. If users add attributes to their arrangement components, reading (resp. writing) arrangement would be done by inheriting the class Arr_file_scanner (resp. Arr_file_writer ) and overriding all the relevant function for scanning (resp. writing) the arrangement components. After the definition of the inherited class users have to call the function read of Arrangement (resp. the global function write_arr ) with the inherited class as a parameter. The ability of sending the Arrangement into a graphic stream as leda_window, Postscript file or Geomview is also provided, users simply have to use the Insertor operator operated on the graphic stream and their arrangement. When users would like to add attributes to their arrangement components and send their arrangement to a graphic stream, they have to inherit the class Pm_drawer and then call the global function draw_pm with this class and their arrangement as parameters. The function Pm_drawer is used both for Planar map and Arrangement, since drawing an arrangement is defined as drawing only its planar map part.

Format As mentioned above, the format of the planar map part is as specified in the Planar Map reference pages (). Here, we are representing the format of the hierarchy tree.

Generally, the format represents the curve nodes list of the arrangement. Each component of one curve node is compound from all the subcurves and edge nodes this curve node contains. This data is associative with geometric information and some topological information in order to be able to update the hierarchy tree efficiently.

The format is detailed below:

  1. The data begins with a line of one integer specifying the number of curve nodes the hierarchy tree has.
  2. The list of curve nodes: each curve node has the following format:
    1. Its associative curve.
    2. An integer specifying the number of levels the curve node has.
    3. The list of all subcurves levels. Each described level goes as follows:
      1. An integer specifying the number of subcurve nodes in the current level.
      2. List of subcurve nodes belong to the current level. Each subcurve consist of the following:
        1. Pointers to subcurves (edge nodes, if the next level is the last) of lower level which are given as the begin and past end indices of children subcurve nodes (edge nodes).
        2. The curve associative with the subcurve node.
    4. An integer specifying the number of edge nodes.
    5. List of edge nodes. Each described edge node goes as follows:
      1. A pointer to an overlapping edge node. This pointer is represented by two indices, the first is an index to a curve node and the second is an index to an edge node defined in that curve node.
      2. An index to the associated halfedge.
      3. The associated curve.

Other rules concerning the format are detailed in the Planar Map reference pages ().

Example of Usage of the I/O Functions

The input of the program is a text file presenting the Arrangement: 

# ------------------------------------- Printing Arrangement
# --------------------------------------------------------
# ------------------------------------- Printing Planar map
# --------------------------------------------------------
# Printing number of vertices halfedges and faces in Planar map
5 8 1
# 5 vertices
# ------------------------------------------
1/1 1/1
0/1 0/1
1/2 1/2
0/1 1/1
1/1 0/1
# 8 halfedges
# ------------------------------------------
2 0/1 0/1 1/2 1/2
1 0/1 0/1 1/2 1/2
0 1/2 1/2 1/1 1/1
2 1/2 1/2 1/1 1/1
2 0/1 1/1 1/2 1/2
3 0/1 1/1 1/2 1/2
2 1/2 1/2 1/1 0/1
4 1/2 1/2 1/1 0/1
# 1 faces
# ------------------------------------------
# writing face
# ------------------------------------------
# UNBOUNDED
# number halfedges on outer boundary
0
# number of holes
1
# inner ccb
# number halfedges on inner boundary
8
0 5 4 2 3 7 6 1 
# finish writing face
# ------------------------------------------
# ------------------------------------- End of Planar map
# --------------------------------------------------------
# Printing curve hierachy
# number of curves
2
# 1 'th curve
# ------------------------------------------
0/1 0/1 1/1 1/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# pair indices (curve node and its edge node) for next overlapping edge node :
0 0
# Halfedge indices associtaed with edge nodes
0
# Edge node curve
0/1 0/1 1/2 1/2
# pair indices (curve node and its edge node) for next overlapping edge node :
0 1
# Halfedge indices associtaed with edge nodes
2
# Edge node curve
1/2 1/2 1/1 1/1
# finished current level
# 2 'th curve
# ------------------------------------------
0/1 1/1 1/1 0/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# pair indices (curve node and its edge node) for next overlapping edge node :
1 0
# Halfedge indices associtaed with edge nodes
4
# Edge node curve
0/1 1/1 1/2 1/2
# pair indices (curve node and its edge node) for next overlapping edge node :
1 1
# Halfedge indices associtaed with edge nodes
7
# Edge node curve
1/2 1/2 1/1 0/1
# finished current level
# ------------------------------------- End of Arrangement
# --------------------------------------------------------

The example above presents an arrangement containing two segments that intersect in their interior. The segments are (0,0) - (1,1) and (0,1) - (1,0). The Arrangement instance that was used to produce this example was templated with the Arr_segment_traits_2 class, which was templated with the representation class Cartesian<Quotient<int> >.

The first part of the input represents the planar map our arrangement contains, and hence its format is identical with . It can be seen that the planar map described here represents all the vertices and halfedges obtained by the disjoint subcurves of the arrangement.

The next part of the input file presents the hierarchy tree of our arrangement. This presentation begins with the number 2, indicating there are two curve nodes in our arrangement. The list of curve nodes follows. The first curve node begins with its associated curve (0,0) - (1,1), it has 0 levels since it does not contain any subcurve nodes (only curve nodes and edge nodes). The number of edge nodes the curve (0,0) - (1,1) induces is two, and the curves these two edge nodes are associated with are (0,0) - (1/2,1/2) and (1/2,1/2) - (1,1) respectively. The indices of each edge node to an overlapping edge node point to the edge node itself since there are no overlapping in the input file. Finally, the indices of the halfedge indicates the halfedge our edge node is associated with. For example, the first edge node induced by the curve (0,0) - (1,1) is associated with the first halfedge presented in the halfedges list. The reader may verify that this halfedge holds the same curve the edge node holds.

The current format may not be comfortable for a user to read, because the usage of indices. There is a possibility to define a verbose format which contains instead of indices, the components themselves, and hence the user has the option to have a format which is easy for human to read. This format cannot be scanned by the reading functions of Arrangement. 

// file: examples/Arrangement_2/example11.C

#include "short_names.h"

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_2_default_dcel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/IO/Arr_iostream.h>
#include <iostream>

#ifdef CGAL_USE_LEDA
// #include <CGAL/IO/Arr_Postscript_file_stream.h>
#endif

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits;
typedef Traits::Curve                                   Curve;
typedef Traits::X_monotone_curve_2                      X_monotone_curve_2;
typedef CGAL::Arr_2_default_dcel<Traits>                Dcel;
typedef CGAL::Arrangement_2<Dcel,Traits>                Arr;

int main()
{
  Arr arr;

  std::cout << "* * * Demonstrating a trivial use of IO functions";
  std::cout << std::endl << std::endl;
  std::cin >> arr;
  std::cout << arr;
  
  std::cout << std::endl;

  std::cout << "* * * Presenting the use of verbose format";
  std::cout << std::endl << std::endl;;
  CGAL::Arr_file_writer<Arr> verbose_writer(std::cout, arr, true);
  CGAL::write_arr(arr, verbose_writer, std::cout);

  // printing to Postscript file.
#ifdef CGAL_USE_LEDA
  //  CGAL::Postscript_file_stream  LPF(500, 500 ,"arr.ps");
  //  LPF.init(-3,3,-3);
  //  LPF.set_line_width( 1);
  //  LPF << arr;
#endif

  return 0;
}

The output is the Arrangement written in both formats, non verbose and verbose. 

* * * Demonstrating a trivial use of IO functions

# ------------------------------------- Printing Arrangement
# --------------------------------------------------------
# ------------------------------------- Begin Planar Map
# --------------------------------------------------------
# Number of vertices halfedges and faces in Planar map
5 8 1
# 5 vertices
# ------------------------------------------
1/1 1/1
0/1 0/1
1/2 1/2
0/1 1/1
1/1 0/1
# 8 halfedges
# ------------------------------------------
2 0/1 0/1 1/2 1/2
1 0/1 0/1 1/2 1/2
0 1/2 1/2 1/1 1/1
2 1/2 1/2 1/1 1/1
2 0/1 1/1 1/2 1/2
3 0/1 1/1 1/2 1/2
2 1/2 1/2 1/1 0/1
4 1/2 1/2 1/1 0/1
# 1 faces
# ------------------------------------------
# writing face
# ------------------------------------------
# UNBOUNDED
# number halfedges on outer boundary
0
# number of holes
1
# inner ccb
# number halfedges on inner boundary
8
0 5 4 2 3 7 6 1 
# finish writing face
# ------------------------------------------
# ------------------------------------- End Planar Map
# --------------------------------------------------------
# Printing curve hierachy
# number of curves
2
# 1 'th curve
# ------------------------------------------
0/1 0/1 1/1 1/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# pair indices (curve node and its edge node) for next overlapping edge node :
0 0
# Halfedge indices associated with edge nodes
0
# Edge node curve
0/1 0/1 1/2 1/2
# pair indices (curve node and its edge node) for next overlapping edge node :
0 1
# Halfedge indices associated with edge nodes
2
# Edge node curve
1/2 1/2 1/1 1/1
# finished current level
# 2 'th curve
# ------------------------------------------
0/1 1/1 1/1 0/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# pair indices (curve node and its edge node) for next overlapping edge node :
1 0
# Halfedge indices associated with edge nodes
4
# Edge node curve
0/1 1/1 1/2 1/2
# pair indices (curve node and its edge node) for next overlapping edge node :
1 1
# Halfedge indices associated with edge nodes
7
# Edge node curve
1/2 1/2 1/1 0/1
# finished current level
# ------------------------------------- End of Arrangement
# --------------------------------------------------------

* * * Presenting the use of verbose format

# ------------------------------------- Printing Arrangement
# --------------------------------------------------------
# ------------------------------------- Begin Planar Map
# --------------------------------------------------------
# Number of vertices halfedges and faces in Planar map
5 8 1
# 5 vertices
# ------------------------------------------
1/1 1/1
0/1 0/1
1/2 1/2
0/1 1/1
1/1 0/1
# 8 halfedges
# ------------------------------------------
0/1 0/1 1/2 1/2 towards  1/2 1/2
0/1 0/1 1/2 1/2 towards  0/1 0/1
1/2 1/2 1/1 1/1 towards  1/1 1/1
1/2 1/2 1/1 1/1 towards  1/2 1/2
0/1 1/1 1/2 1/2 towards  1/2 1/2
0/1 1/1 1/2 1/2 towards  0/1 1/1
1/2 1/2 1/1 0/1 towards  1/2 1/2
1/2 1/2 1/1 0/1 towards  1/1 0/1
# 1 faces
# ------------------------------------------
# writing face
# ------------------------------------------
# UNBOUNDED
# number halfedges on outer boundary
0
# number of holes
1
# inner ccb
# number halfedges on inner boundary
8
0/1 0/1 1/2 1/2 towards  1/2 1/2
0/1 1/1 1/2 1/2 towards  0/1 1/1
0/1 1/1 1/2 1/2 towards  1/2 1/2
1/2 1/2 1/1 1/1 towards  1/1 1/1
1/2 1/2 1/1 1/1 towards  1/2 1/2
1/2 1/2 1/1 0/1 towards  1/1 0/1
1/2 1/2 1/1 0/1 towards  1/2 1/2
0/1 0/1 1/2 1/2 towards  0/1 0/1

# finish writing face
# ------------------------------------------
# ------------------------------------- End Planar Map
# --------------------------------------------------------
# Printing curve hierachy
# number of curves
2
# 1 'th curve
# ------------------------------------------
0/1 0/1 1/1 1/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# Halfedge associated with edge nodes
0/1 0/1 1/2 1/2 towards  1/2 1/2
# Edge node curve
0/1 0/1 1/2 1/2
# Halfedge associated with edge nodes
1/2 1/2 1/1 1/1 towards  1/1 1/1
# Edge node curve
1/2 1/2 1/1 1/1
# finished current level
# 2 'th curve
# ------------------------------------------
0/1 1/1 1/1 0/1
# number of levels
0
# number of edge nodes
2
# ----------------------- Edge nodes childrens:
# Halfedge associated with edge nodes
0/1 1/1 1/2 1/2 towards  1/2 1/2
# Edge node curve
0/1 1/1 1/2 1/2
# Halfedge associated with edge nodes
1/2 1/2 1/1 0/1 towards  1/1 0/1
# Edge node curve
1/2 1/2 1/1 0/1
# finished current level
# ------------------------------------- End of Arrangement
# --------------------------------------------------------

For more examples see chapter .

More details are given in sections Arr_file_scanner<Arrangement>, Arr_file_writer<Arrangement>
end of advanced section  advanced  end of advanced section

Next chapter: 2D Arrangements
Navigation: Table of Contents, Bibliography, Index, Title Page
The CGAL Project . Tue, December 21, 2004 .