
 |
Multiplying the transformation matrix by a scalar does not change the represented transformation. Therefore, any transformation represented by a matrix with rational entries can be represented by a transformation matrix with integer entries as well. (Multiply the matrix with the common denominator of the rational entries.) Hence, it is sufficient to use the number type Kernel::RT to represent the entries of the transformation matrix.
CGAL offers several specialized affine transformations. Different constructors are provided to create them. They are parameterized with a symbolic name to denote the transformation type, followed by additional parameters. The symbolic name tags solve ambiguities in the function overloading and they make the code more readable, i.e., what type of transformation is created.
Since two-dimensional points have three homogeneous coordinates, we have a matrix .
If the homogeneous representations are normalized (the homogenizing coordinate is 1), then the upper left matrix realizes linear transformations. In the matrix form of a translation, the translation vector appears in the last column of the matrix. The entries and are always zero and therefore do not appear in the constructors.
|
| |||
|
introduces an identity transformation.
| |||
|
| |||
|
introduces a translation by a vector .
| |||
| |||
|
approximates the rotation over the angle indicated by direction
, such that the differences between the sines and cosines
of the rotation given by d and the approximating rotation
are at most each. Precondition: .
| |||
| |||
|
introduces a rotation by the angle rho. Precondition: .
| |||
| |||
|
introduces a scaling by a scale factor .
| |||
| |||
introduces a general affine transformation in the
3x3 matrix  .
The sub-matrix .
The sub-matrix 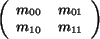 contains the scaling and rotation
information, the vector contains the scaling and rotation
information, the vector
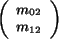 contains the translational part of the transformation.
contains the translational part of the transformation.
| |||
| |||
introduces a general linear transformation
 ,
i.e. there is no translational part. ,
i.e. there is no translational part.
| |||
The main thing to do with transformations is to apply them on geometric objects. Each class Class_2<Kernel> representing a geometric object has a member function:
Class_2<Kernel> transform(Aff_transformation_2<Kernel> t).
The transformation classes provide a member function transform() for points, vectors, directions, and lines:
|
|
| |
|
|
| |
|
| ||
|
| ||
|
|
| |
CGAL provides function operators for these member functions:
|
|
| |
|
|
| |
|
| ||
|
| ||
|
|
| |
|
| ||
|
| composes two affine transformations. | |
|
| ||
|
| gives the inverse transformation. | |
|
|
| returns true, if the transformation is not reflecting, i.e. the determinant of the involved linear transformation is non-negative. |
|
|
| returns true, if the transformation is reflecting. |
The matrix entries of a matrix representation of a Aff_transformation_2<Kernel> can be accessed trough the following member functions:
|
|
| |
|
|
| |
| returns entry in a matrix representation in which is 1. | ||
|
|
| |
|
|
| |
| returns entry in some fixed matrix representation. | ||
For affine transformations no I/O operators are defined.
typedef Cartesian<double> K; typedef Aff_transformation_2<K> Transformation; typedef Point_2<K> Point; typedef Vector_2<K> Vector; typedef Direction_2<K> Direction; Transformation rotate(ROTATION, sin(pi), cos(pi)); Transformation rational_rotate(ROTATION,Direction(1,1), 1, 100); Transformation translate(TRANSLATION, Vector(-2, 0)); Transformation scale(SCALING, 3); Point q(0, 1); q = rational_rotate(q); Point p(1, 1); p = rotate(p); p = translate(p); p = scale(p);
The same would have been achieved with
Transformation transform = scale * (translate * rotate); p = transform(Point(1.0, 1.0));