Chapter 52
2D and Surface Function Interpolation

Julia Flötotto

Table of Contents

This chapter describes CGAL's interpolation package which implements natural neighbor coordinate functions as well as different methods for scattered data interpolation most of which are based on natural neighbor coordinates. The functions for computing natural neighbor coordinates in Euclidean space are described in Section 52.1, the functions concerning the coordinate and neighbor computation on surfaces are discussed in Section 52.2. In Section 52.3, we describe the different interpolation functions.

Scattered data interpolation solves the following problem: given measures of a function on a set of discrete data points, the task is to interpolate this function on an arbitrary query point. More formally, let $$={p₁,...,p_n} be a set of $$n points in $$ ² or $$ ³ and $$ be a scalar function defined on the convex hull of $$. We assume that the function values are known at the points of $$, i.e. to each $$p_i , we associate $$z_i = (p_i). Sometimes, the gradient of $$ is also known at $$p_i. It is denoted $$g_i= (p_i). The interpolation is carried out for an arbitrary query point $$x on the convex hull of $$.

52.1   Natural Neighbor Coordinates

52.1.1   Introduction

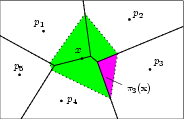
Figure 52.1:  $$2D example: $$x has five natural neighbors $$p₁,..., p₅. The natural neighbor coordinate $$₃(x) is the ratio of the area of the pink polygon, $$₃(x), over the area of the total highlighted zone.

Let $$(x) denote the volume of the potential Voronoi cell of $$x and $$_i(x) denote the volume of the sub-cell that would be stolen from the cell of $$p_i by the cell of $$x. The natural neighbor coordinate of $$x with respect to the data point $$p_i is defined by

$$ _i(x) = (_i(x))/((x)).

A two-dimensional example is depicted in Figure 52.1.

Various papers ([Sib80], [Far90], [Pip93], [Bro97], [HS00]) show that the natural neighbor coordinates have the following properties:

(i)
$$x = _i=1ⁿ _i(x) p_i (barycentric coordinate property).
(ii)
For any $$i,j n, _i(p_j)= _ij, where $$_ij is the Kronecker symbol.
(iii)
$$ _i=1ⁿ _i(x) = 1 (partition of unity property).

$$(x) =

$$_i(x) = 0 for all data point $$p_i of $$ except for the two endpoints, let's say $$p and $$q ,of the edge where x lies.

The natural neighbor coordinate of $$x with respect to these endpoints $$p and $$q will be :

$$_p(x) = ( x - q )/( q - p )

$$_q(x) = ( x - p )/( q - p )

Furthermore, Piper [Pip93] shows that the coordinate functions are continuous in the convex hull of $$ and continuously differentiable except on the data points $$.

The interpolation package of CGAL provides functions to compute natural neighbor coordinates for $$2D and $$3D points with respect to Voronoi diagrams as well as with respect to power diagrams (only $$2D), i.e. for weighted points. Refer to the reference pages natural_neighbor_coordinates_2, natural_neighbor_coordinates_3 and regular_neighbor_coordinates_2.

In addition, the package provides functions to compute natural neighbor coordinates on well sampled point set surfaces. See Section 52.2 and the reference page surface_neighbor_coordinates_3 for further information.

52.1.2   Implementation

_i(x)

(x)

52.1.3   Example for Natural Neighbor Coordinates

The signature of all coordinate computation functions is about the same.

File: examples/Interpolation/nn_coordinates_2.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/natural_neighbor_coordinates_2.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};
typedef CGAL::Delaunay_triangulation_2<K>             Delaunay_triangulation;
typedef std::vector< std::pair< K::Point_2, K::FT  > >
                                                      Point_coordinate_vector;

int main()
{
  Delaunay_triangulation dt;

  for (int y=0 ; y<3 ; y++)
    for (int x=0 ; x<3 ; x++)
      dt.insert(K::Point_2(x,y));

  //coordinate computation
  K::Point_2 p(1.2, 0.7);
  Point_coordinate_vector coords;
  CGAL::Triple<
    std::back_insert_iterator<Point_coordinate_vector>,
    K::FT, bool> result =
    CGAL::natural_neighbor_coordinates_2(dt, p,
					 std::back_inserter(coords));
  if(!result.third){
    std::cout << "The coordinate computation was not successful."
	      << std::endl;
    std::cout << "The point (" <<p << ") lies outside the convex hull."
	      << std::endl;
  }
  K::FT  norm = result.second;
  std::cout << "Coordinate computation successful." << std::endl;
  std::cout << "Normalization factor: " <<norm << std::endl;
  std::cout << "done" << std::endl;
  return 0;
}

52.1.4   Example for Regular Neighbor Coordinates

File: examples/Interpolation/rn_coordinates_2.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Regular_triangulation_2.h>
#include <CGAL/Regular_triangulation_euclidean_traits_2.h>
#include <CGAL/regular_neighbor_coordinates_2.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};

typedef CGAL::Regular_triangulation_euclidean_traits_2<K> Gt;
typedef CGAL::Regular_triangulation_2<Gt>              Regular_triangulation;
typedef Regular_triangulation::Weighted_point Weighted_point;
typedef std::vector< std::pair< Weighted_point, K::FT  > >
                                                       Point_coordinate_vector;

int main()
{
  Regular_triangulation rt;

  for (int y=0 ; y<3 ; y++)
    for (int x=0 ; x<3 ; x++)
      rt.insert(Weighted_point(K::Point_2(x,y), 0));

  //coordinate computation
  Weighted_point wp(K::Point_2(1.2, 0.7),2);
  Point_coordinate_vector  coords;
  CGAL::Triple<
    std::back_insert_iterator<Point_coordinate_vector>,
    K::FT, bool> result =
    CGAL::regular_neighbor_coordinates_2(rt, wp,
					 std::back_inserter(coords));
  if(!result.third){
    std::cout << "The coordinate computation was not successful."
	      << std::endl;
    std::cout << "The point (" <<wp.point() << ") lies outside the convex hull."
	      << std::endl;
  }
  K::FT  norm = result.second;
  std::cout << "Coordinate computation successful." << std::endl;
  std::cout << "Normalization factor: " <<norm << std::endl;

  std::cout << "done" << std::endl;
  return 0;
}

52.2   Surface Natural Neighbor Coordinates and Surface Neighbors

This section introduces the functions to compute natural neighbor coordinates and surface neighbors associated to a set of sample points issued from a surface $$ and given a query point $$x on $$. We suppose that $$ is a closed and compact surface of $$ ³, and let $$= {p₁, ...,p_n} be an $$-sample of $$ (refer to Amenta and Bern [AB99]). The concepts are based on the definition of Boissonnat and Flötotto [BF02], [Flö03b]. Both references contain a thorough description of the requirements and the mathematical properties.

52.2.1   Introduction

Two observations lead to the definition of surface neighbors and surface neighbor coordinates: First, it is clear that the tangent plane $$_x of the surface $$ at the point $$x approximates $$ in the neighborhood of $$x. It has been shown in [BF02] that, if the surface $$ is well sampled with respect to the curvature and the local thickness of $$, i.e. it is an $$-sample, the intersection of the tangent plane $$_x with the Voronoi cell of $$x in the Voronoi diagram of $$ {x} has a small diameter. Consequently, inside this Voronoi cell, the tangent plane $$_x is a reasonable approximation of $$. Furthermore, the second observation allows to compute this intersection diagram easily: one can show using Pythagoras' Theorem that the intersection of a three-dimensional Voronoi diagram with a plane $$ is a two-dimensional power diagram. The points defining the power diagram are the projections of the points in $$ onto $$, each point weighted with its negative square distance to $$. Algorithms for the computation of power diagrams via the dual regular triangulation are well known and for example provided by CGAL in the class Regular_triangulation_2<Gt, Tds>.

52.2.2   Implementation

Voronoi Intersection Diagrams

In CGAL, the regular triangulation dual to the intersection of a $$3D Voronoi diagram with a plane $$ can be computed by instantiating the Regular_triangulation_2<Gt, Tds> class with the traits class Voronoi_intersection_2_traits_3<K>. This traits class contains a point and a vector as class member which define the plane $$. All predicates and constructions used by Regular_triangulation_2<Gt, Tds> are replaced by the corresponding operators on three-dimensional points. For example, the power test predicate (which takes three weighted $$2D points $$p', $$q', $$r' of the regular triangulation and tests the power distance of a fourth point $$t' with respect to the power circle orthogonal to $$p, $$q, $$r) is replaced by a Side_of_plane_centered_sphere_2_3 predicate that tests the position of a $$3D point $$t with respect to the sphere centered on the plane $$ passing through the $$3D points $$p, $$q, $$r. This approach allows to avoid the explicit constructions of the projected points and the weights which are very prone to rounding errors.

Natural Neighbor Coordinates on Surfaces

The computation of natural neighbor coordinates on surfaces is based upon the computation of regular neighbor coordinates with respect to the regular triangulation that is dual to $$Vor() _x, the intersection of $$_x and the Voronoi diagram of $$, via the function regular_neighbor_coordinates_2.

Of course, we might introduce all data points $$ into this regular triangulation. However, this is not necessary because we are only interested in the cell of $$x. It is sufficient to guarantee that all surface neighbors of the query point $$x are among the input points that are passed as argument to the function. The sample points $$ can be filtered for example by distance, e.g. using range search or $$k-nearest neighbor queries, or with the help of the $$3D Delaunay triangulation since the surface neighbors are necessarily a subset of the natural neighbors of the query point in this triangulation. CGAL provides a function that encapsulates the filtering based on the $$3D Delaunay triangulation. For input points filtered by distance, functions are provided that indicate whether or not points that lie outside the input range (i.e. points that are further from $$x than the furthest input point) can still influence the result. This allows to iteratively enlarge the set of input points until the range is sufficient to certify the result.

Surface Neighbors

The surface neighbors of the query point are its neighbors in the regular triangulation that is dual to $$Vor() _x, the intersection of $$_x and the Voronoi diagram of $$. As for surface neighbor coordinates, this regular triangulation is computed and the same kind of filtering of the data points as well as the certification described above is provided.

52.2.3   Example for Surface Neighbor Coordinates

File: examples/Interpolation/surface_neighbor_coordinates_3.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>

#include <CGAL/point_generators_3.h>
#include <CGAL/copy_n.h>
#include <CGAL/Origin.h>

#include <CGAL/surface_neighbor_coordinates_3.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};
typedef K::FT                      Coord_type;
typedef K::Point_3                 Point_3;
typedef K::Vector_3                Vector_3;
typedef std::vector< std::pair< Point_3, K::FT  > >
                                   Point_coordinate_vector;

int main()
{

  int n=100;
  std::vector< Point_3> points;
  points.reserve(n);

  std::cout << "Generate " << n << " random points on a sphere."
	    << std::endl;
  CGAL::Random_points_on_sphere_3<Point_3> g(1);
  CGAL::copy_n( g, n, std::back_inserter(points));

  Point_3 p(1, 0,0);
  Vector_3 normal(p-CGAL::ORIGIN);
  std::cout << "Compute surface neighbor coordinates for "
	    << p << std::endl;
  Point_coordinate_vector coords;
  CGAL::Triple< std::back_insert_iterator<Point_coordinate_vector>,
    K::FT, bool> result =
    CGAL::surface_neighbor_coordinates_3(points.begin(), points.end(),
					 p, normal,
					 std::back_inserter(coords),
					 K());
  if(!result.third){
    //Undersampling:
    std::cout << "The coordinate computation was not successful."
	      << std::endl;
    return 0;
  }
  K::FT norm = result.second;

  std::cout << "Testing the barycentric property " << std::endl;
  Point_3 b(0, 0,0);
  for(std::vector< std::pair< Point_3, Coord_type  > >::const_iterator
	it = coords.begin(); it!=coords.end(); ++it)
    b = b + (it->second/norm)* (it->first - CGAL::ORIGIN);

  std::cout <<"    weighted barycenter: " << b <<std::endl;
  std::cout << "    squared distance: " <<
    CGAL::squared_distance(p,b) <<std::endl;

  std::cout << "done" << std::endl;
  return 0;
}

52.3   Interpolation Methods

52.3.1   Introduction

Linear Precision Interpolation

Sibson [Sib81] defines a very simple interpolant that re-produces linear functions exactly. The interpolation of $$(x) is given as the linear combination of the neighbors' function values weighted by the coordinates:

$$ Z⁰(x) = _{i i}(x) z_i.

Indeed, if $$z_i=a + b^t p_i for all natural neighbors of $$x, we have

$$ Z⁰(x) = _{i i}(x) (a + b^tp_i) = a+b^t x

by the barycentric coordinate property. The first example in Subsection 52.3.3 shows how the function is called.

Sibson's $$C¹ Continuous Interpolant

p_i

(x) =a + b^t x + x^tx

Sibson's $$Z¹ interpolant is a combination of the linear interpolant $$Z⁰ and an interpolant $$ which is the weighted sum of the first degree functions

$$_i(x) = z_i +g_i^t(x-p_i),    (x)= ( _i (_i(x))/( x-p_i )_i(x) )/( _i (_i(x))/( x-p_i )).

Sibson observed that the combination of $$Z⁰ and $$ reconstructs exactly a spherical quadric if they are mixed as follows:

$$ Z¹(x) = ((x) Z⁰(x) + (x) (x))/((x) + (x)) where (x) = ( _{i i}(x) ( x - p_i ²)/(f( x - p_i )))/( _i (_i(x))/(f( x - p_i ))) and (x)= _{i i}(x) x - p_i ²,

where in Sibson's original work, $$f( x - p_i ) = x - p_i .

CGAL contains a second implementation with $$f( x - p_i ) = x - p_i ² which is less demanding on the number type because it avoids the square-root computation needed to compute the distance $$ x - p_i . The theoretical guarantees are the same (see [Flö03b]). Simply, the smaller the slope of $$f around $$f(0), the faster the interpolant approaches $$_i as $$x p_i.

Farin's $$C¹ Continuous Interpolant

Farin [Far90] extended Sibson's work and realizes a $$C¹ continuous interpolant by embedding natural neighbor coordinates in the Bernstein-Bézier representation of a cubic simplex. If the gradient of $$ at the data points is known, this interpolant reproduces quadratic functions exactly. The function gradient can be approximated from the function values by Sibson's method [Sib81] (see Section 52.3.2) which is exact only for spherical quadrics.

Quadratic Precision Interpolants

Knowing the gradient $$g_i for all $$p_i , we formulate a very simple interpolant that reproduces exactly quadratic functions. This interpolant is not $$C¹ continuous in general. It is defined as follows:

$$ I¹(x) = _{i i}(x) (z_i + (1)/(2) g_i^t (x - p_i))

52.3.2   Gradient Fitting

$$g_i = min$$_{g j} (_j(p_i))/( p_i - p_j ²) ( z_j - (z_i + g^t (p_j -p_i)) ),

where $$_j(p_i) is the natural neighbor coordinate of $$p_i with respect to $$p_i associated to $$ {p_i}. For spherical quadrics, the result is exact.

CGAL provides functions to approximate the gradients of all data points that are inside the convex hull. There is one function for each type of natural neighbor coordinate (i.e. natural_neighbor_coordinates_2, regular_neighbor_coordinates_2).

52.3.3   Example for Linear Interpolation

File: examples/Interpolation/linear_interpolation_2.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>

#include <CGAL/Interpolation_traits_2.h>
#include <CGAL/natural_neighbor_coordinates_2.h>
#include <CGAL/interpolation_functions.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};
typedef CGAL::Delaunay_triangulation_2<K>             Delaunay_triangulation;
typedef CGAL::Interpolation_traits_2<K>               Traits;
typedef K::FT                                         Coord_type;
typedef K::Point_2                                    Point;

int main()
{
  Delaunay_triangulation T;
  std::map<Point, Coord_type, K::Less_xy_2> function_values;
  typedef CGAL::Data_access< std::map<Point, Coord_type, K::Less_xy_2 > >
                                            Value_access;

  Coord_type a(0.25), bx(1.3), by(-0.7);

  for (int y=0 ; y<3 ; y++)
    for (int x=0 ; x<3 ; x++){
      K::Point_2 p(x,y);
      T.insert(p);
      function_values.insert(std::make_pair(p,a + bx* x+ by*y));
    }
  //coordinate computation
  K::Point_2 p(1.3,0.34);
  std::vector< std::pair< Point, Coord_type > > coords;
  Coord_type norm =
    CGAL::natural_neighbor_coordinates_2
    (T, p,std::back_inserter(coords)).second;

  Coord_type res =  CGAL::linear_interpolation(coords.begin(), coords.end(),
				               norm,
					       Value_access(function_values));

  std::cout << "   Tested interpolation on " << p << " interpolation: "
	    << res << " exact: " << a + bx* p.x()+ by* p.y()<< std::endl;

  std::cout << "done" << std::endl;
  return 0;
}

52.3.4   Example for Sibson's $$C¹ Interpolation Scheme with Gradient Estimation

File: examples/Interpolation/sibson_interpolation_2.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>

#include <CGAL/natural_neighbor_coordinates_2.h>
#include <CGAL/Interpolation_gradient_fitting_traits_2.h>
#include <CGAL/sibson_gradient_fitting.h>
#include <CGAL/interpolation_functions.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};
typedef CGAL::Delaunay_triangulation_2<K>               Delaunay_triangulation;
typedef CGAL::Interpolation_gradient_fitting_traits_2<K> Traits;

typedef K::FT                                            Coord_type;
typedef K::Point_2                                       Point;
typedef std::map<Point, Coord_type, K::Less_xy_2>        Point_value_map ;
typedef std::map<Point, K::Vector_2 , K::Less_xy_2 >     Point_vector_map;

int main()
{
  Delaunay_triangulation T;

  Point_value_map function_values;
  Point_vector_map function_gradients;

  //parameters for spherical function:
  Coord_type a(0.25), bx(1.3), by(-0.7), c(0.2);
  for (int y=0 ; y<4 ; y++)
    for (int x=0 ; x<4 ; x++){
      K::Point_2 p(x,y);
      T.insert(p);
      function_values.insert(std::make_pair(p,a + bx* x+ by*y + c*(x*x+y*y)));
    }
  sibson_gradient_fitting_nn_2(T,std::inserter(function_gradients,
					       function_gradients.begin()),
			       CGAL::Data_access<Point_value_map>
			       (function_values),
			       Traits());


  //coordiante computation
  K::Point_2 p(1.6,1.4);
  std::vector< std::pair< Point, Coord_type > > coords;
  Coord_type norm =
    CGAL::natural_neighbor_coordinates_2(T, p,std::back_inserter
					 (coords)).second;


  //Sibson interpolant: version without sqrt:
  std::pair<Coord_type, bool> res =
    CGAL::sibson_c1_interpolation_square
    (coords.begin(),
     coords.end(),norm,p,
     CGAL::Data_access<Point_value_map>(function_values),
     CGAL::Data_access<Point_vector_map>(function_gradients),
     Traits());
  if(res.second)
    std::cout << "   Tested interpolation on " << p
	      << " interpolation: " << res.first << " exact: "
	      << a + bx * p.x()+ by * p.y()+ c*(p.x()*p.x()+p.y()*p.y())
	      << std::endl;
  else
    std::cout << "C^1 Interpolation not successful." << std::endl
	      << " not all function_gradients are provided."  << std::endl
	      << " You may resort to linear interpolation." << std::endl;

  std::cout << "done" << std::endl;
  return 0;
}

An additional example in the distribution compares numerically the errors of the different interpolation functions with respect to a known function. It is distributed in the examples directory.