Chapter 51
Principal Component Analysis

Pierre Alliez and Sylvain Pion

Table of Contents

This CGAL package provides functions to compute global information on the shape of a set of 2D or 3D objects such as points. It provides the computation of axis-aligned bounding boxes, centroids of point sets, barycenters of weighted point sets, as well as linear least squares fitting for point sets in 2D, and point sets as well as triangle sets in 3D. The sets are specified by iterator ranges of containers.

51.1   Definitions

A bounding box for a set of objects is a cuboid that completely contains the set. An axis-aligned bounding box is a bounding box aligned with the axes of the coordinate system.

A centroid is defined as average of position. A barycenter of weighted point sets is defined as weighted average of position. When all weights are equal the barycenter coincides with the centroid.

Given a point set, linear least squares fitting amounts to find the linear sub-space which minimizes the sum of squared distances from the points to their projection onto this linear sub-space. This problem is equivalent to search for the linear sub-space which maximizes the variance of projected points, the latter being obtained by eigen decomposition of the covariance matrix of the point set. Eigenvectors corresponding to large eigenvalues are the directions in which the data has strong component, or equivalently large variance. If eigenvalues are the same there is no preferable sub-space.

Given a triangle set, linear least squares fitting amounts to find the linear sub-space which minimizes the sum of squared distances from all points in the set to their projection onto this linear sub-space. This problem is equivalent to the one of fitting a linear sub-space to a point set, except that the covariance matrix is now derived from a continuous integral over the triangles instead of a discrete sum over the points.

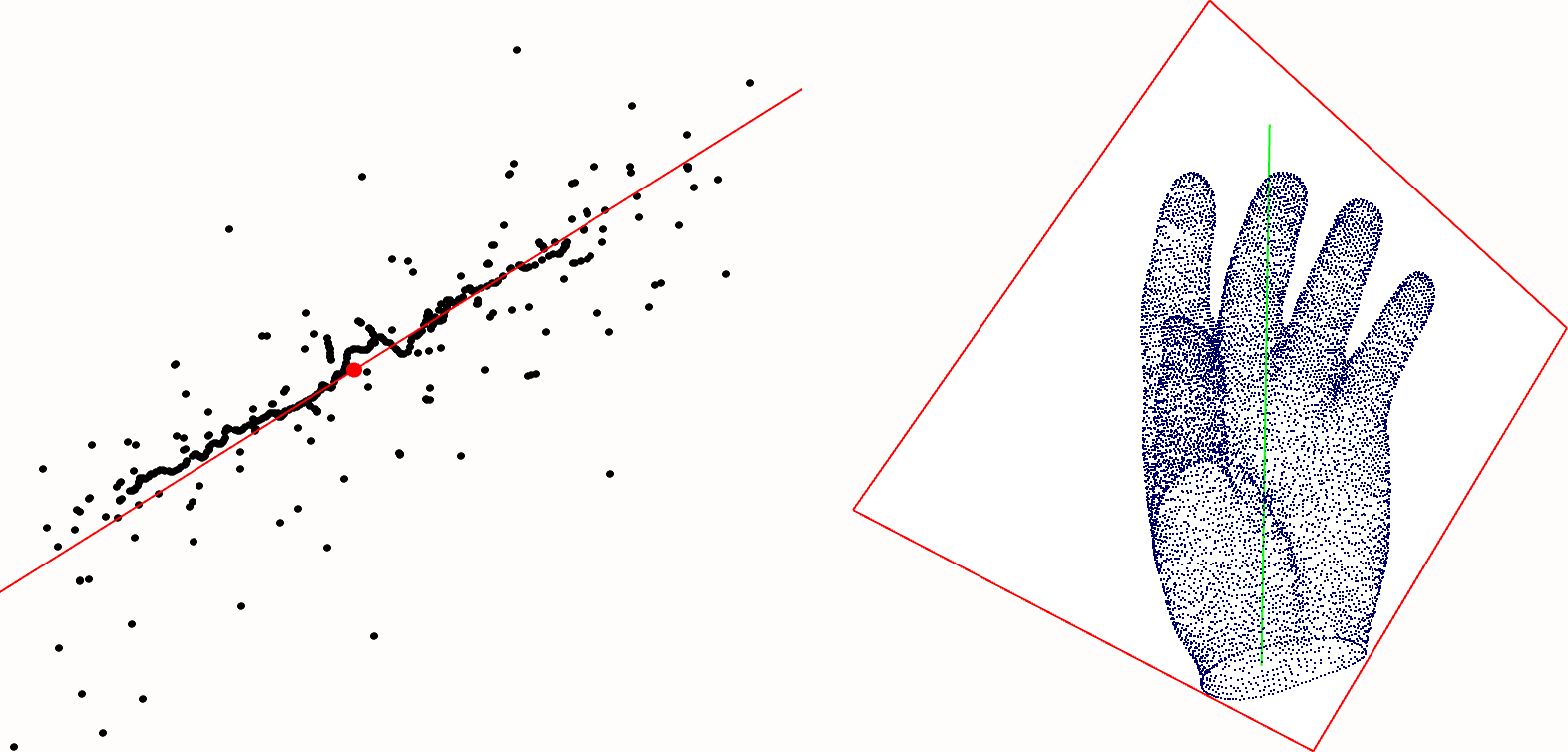
Figure 51.1:  Left: fitting a line to a 2D point set. Right: fitting a line and a plane to a 3D point set.

51.2   Examples

51.2.1   Bounding Box of a Point Set

In the following example we use STL containers of 2D and 3D points, and compute their axis-aligned bounding box. The kernel from which the input points come is automatically deduced by the function.

File: examples/Principal_component_analysis/bounding_box.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/bounding_box.h>

#include <list>
#include <iostream>

typedef double              FT;
typedef CGAL::Cartesian<FT> K;
typedef K::Point_2          Point_2;
typedef K::Point_3          Point_3;

int main()
{
  // axis-aligned bounding box of 2D points
  std::list<Point_2> points_2;
  points_2.push_back(Point_2(1.0, 0.0));
  points_2.push_back(Point_2(2.0, 2.0));
  points_2.push_back(Point_2(3.0, 5.0));

  K::Iso_rectangle_2 c2 = CGAL::bounding_box(points_2.begin(), points_2.end());
  std::cout << c2 << std::endl;

  // axis-aligned bounding box of 3D points
  std::list<Point_3> points_3;
  points_3.push_back(Point_3(1.0, 0.0, 0.5));
  points_3.push_back(Point_3(2.0, 2.0, 1.2));
  points_3.push_back(Point_3(3.0, 5.0, 4.5));

  K::Iso_cuboid_3 c3 = CGAL::bounding_box(points_3.begin(), points_3.end());
  std::cout << c3 << std::endl;

  return 0;
}

51.2.2   Centroid of a Point Set

In the following example we use STL containers of 2D and 3D points, and compute their centroid. The kernel from which the input points come is automatically deduced by the function.

File: examples/Principal_component_analysis/centroid.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/centroid.h>

#include <list>
#include <iostream>

typedef double               FT;
typedef CGAL::Cartesian<FT>  K;
typedef K::Point_2           Point_2;
typedef K::Point_3           Point_3;

int main()
{
  // centroid of 2D points
  std::list<Point_2> points_2;
  points_2.push_back(Point_2(1.0, 0.0));
  points_2.push_back(Point_2(2.0, 2.0));
  points_2.push_back(Point_2(3.0, 5.0));

  Point_2 c2 = CGAL::centroid(points_2.begin(), points_2.end());
  std::cout << c2 << std::endl;

  // centroid of 3D points
  std::list<Point_3> points_3;
  points_3.push_back(Point_3(1.0, 0.0, 0.5));
  points_3.push_back(Point_3(2.0, 2.0, 1.2));
  points_3.push_back(Point_3(3.0, 5.0, 4.5));

  Point_3 c3 = CGAL::centroid(points_3.begin(), points_3.end());
  std::cout << c3 << std::endl;

  return 0;
}

51.2.3   Barycenter of a Set of Weighted Points

In the following example we use STL containers of 2D and 3D weighted points, and compute their barycenter. The kernel from which the input points come is automatically deduced by the function.

File: examples/Principal_component_analysis/barycenter.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/barycenter.h>

#include <list>
#include <iostream>
#include <utility>

typedef double               FT;
typedef CGAL::Cartesian<FT>  K;
typedef K::Point_2           Point_2;
typedef K::Point_3           Point_3;

int main()
{
  // barycenter of 2D points
  std::list<std::pair<Point_2, FT> > points_2;
  points_2.push_back(std::make_pair(Point_2(1.0, 0.0),  1.0));
  points_2.push_back(std::make_pair(Point_2(2.0, 2.0),  2.0));
  points_2.push_back(std::make_pair(Point_2(3.0, 5.0), -2.0));

  Point_2 c2 = CGAL::barycenter(points_2.begin(), points_2.end());
  std::cout << c2 << std::endl;

  // barycenter of 3D points
  std::list<std::pair<Point_3, FT> > points_3;
  points_3.push_back(std::make_pair(Point_3(1.0, 0.0, 0.5),  1.0));
  points_3.push_back(std::make_pair(Point_3(2.0, 2.0, 1.2),  2.0));
  points_3.push_back(std::make_pair(Point_3(3.0, 5.0, 4.5), -5.0));

  Point_3 c3 = CGAL::barycenter(points_3.begin(), points_3.end());
  std::cout << c3 << std::endl;

  return 0;
}

51.2.4   Best Fitting Line of a 2D Point Set

In the following example we use an STL container of 2D points, and compute the best fitting line. The kernel from which the input points come is automatically deduced by the function.

File: examples/Principal_component_analysis/linear_least_squares_fitting.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/linear_least_squares_fitting_2.h>

typedef double               FT;
typedef CGAL::Cartesian<FT>  K;
typedef K::Line_2            Line_2;
typedef K::Point_2           Point_2;

int main()
{
  std::list<Point_2> points;
  points.push_back(Point_2(1.0,0.0));
  points.push_back(Point_2(2.0,0.0));
  points.push_back(Point_2(3.0,0.0));

  Line_2 line;
  linear_least_squares_fitting_2(points.begin(),points.end(),line);

  return 0;
}