CGAL::Quadratic_program<NT>
#include <CGAL/QP_models.h>
Definition
An object of class Quadratic_program<NT> describes a convex quadratic program of the form
in n real variables x=(x0,...,xn-1).
Here,
- A is an m × n matrix (the constraint matrix),
- b is an m-dimensional vector (the right-hand side),
- ~ is an m-dimensional vector of relations
from {
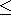 , =,
, =,  },
},
- l is an n-dimensional vector of lower
bounds for x, where lj
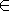
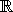
 {-
{- 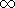 } for all j
} for all j
- u is an n-dimensional vector of upper bounds for
x, where uj
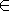
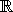
 {
{ 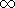 } for all j
} for all j
- D is a symmetric positive-semidefinite n × n matrix (the
quadratic objective function),
- c is an n-dimensional vector (the linear objective
function), and
- c0 is a constant.
If D=0, the program is
a linear program; if the variable bounds are x  0, we have a
nonnegative program.
0, we have a
nonnegative program.
This class allows you to build your program entry by entry, using
the set-methods below.
If you only need to wrap existing (random-access)
iterators over your own data, then you may use any of the four models
Quadratic_program_from_iterators<A_it, B_it, R_it, FL_it, L_it, FU_it, U_it, D_it, C_it>,
Linear_program_from_iterators<A_it, B_it, R_it, FL_it, L_it, FU_it, U_it, C_it>,
Nonnegative_quadratic_program_from_iterators<A_it, B_it, R_it, D_it, C_it>, and
Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it>.
If you want to read a quadratic program in MPSFormat from a stream,
please use the model Quadratic_program_from_mps<NT>.
Is Model for the Concepts
QuadraticProgram
LinearProgram
NonnegativeQuadraticProgram
NonnegativeLinearProgram
Types
|
Quadratic_program<NT>::NT
|
|
The number type of the program entries.
|
Creation
|
Quadratic_program<NT> qp ( |
CGAL::Comparison_result default_r = CGAL::EQUAL,
bool default_fl = true,
NT default_l = 0,
bool default_fu = false,
NT default_u = 0); |
|
|
constructs a quadratic program with no variables and no constraints, ready
for data to be added. Unless relations are explicitly set, they will
be of type default_r. Unless bounds are explicitly set, they
will be as specified by default_fl (finite lower bound?),
default_l (lower bound value if lower bound is finite),
default_fu (finite upper bound?), and
default_l (upper bound value if upper bound is finite). If all
parameters take their default values, we thus get equality constraints
and bounds x  0 by default. Numerical entries that are not
explicitly set will default to 0. 0 by default. Numerical entries that are not
explicitly set will default to 0.| Precondition: | if
default_fl=default_fu=true, then
default_l 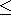 default_u default_u |
|
Operations
|
bool
|
qp.is_linear ()
|
returns true if and only if
qp is a linear program.
|
|
|
bool
|
qp.is_nonnegative ()
|
returns true if and only if
qp is a nonnegative program.
|
|
|
void
|
qp.set_a ( int j, int i, NT val)
|
sets the entry Aij
in column j and row i of the constraint matrix A of qp to
val. An existing entry is overwritten. qp is enlarged if
necessary to accomodate this entry.
|
|
|
void
|
qp.set_b ( int i, NT val)
|
sets the entry bi
of qp to val. An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry.
|
|
|
void
|
qp.set_r ( int i, CGAL::Comparison_result rel)
|
| |
sets the entry ~ i of qp to rel. CGAL::SMALLER
means that the i-th constraint is of type `` 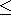 '', CGAL::EQUAL
means ``='', and CGAL::LARGER encodes `` '', CGAL::EQUAL
means ``='', and CGAL::LARGER encodes ``  ''. An existing entry
is overwritten. qp is enlarged if necessary to accomodate this entry. ''. An existing entry
is overwritten. qp is enlarged if necessary to accomodate this entry.
|
|
|
void
|
qp.set_l ( int j, bool is_finite, NT val = NT(0))
|
| |
if is_finite, this sets the entry lj of qp to val,
otherwise it sets lj to - 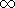 . An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry. . An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry.
|
|
|
void
|
qp.set_u ( int j, bool is_finite, NT val = NT(0))
|
| |
if is_finite, this sets the entry uj of qp to val,
otherwise it sets uj to 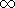 . An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry. . An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry.
|
|
|
void
|
qp.set_c ( int j, NT val)
|
sets the entry cj
of qp to val. An existing entry is overwritten.
qp is enlarged if necessary to accomodate this entry.
|
|
|
void
|
qp.set_c0 ( NT val)
|
sets the entry c0
of qp to val. An existing entry is overwritten.
|
|
|
void
|
qp.set_d ( int i, int j, NT val)
|
sets the entries
2Dij and 2Dji of qp to val. Existing entries are
overwritten. qp is enlarged if necessary to accomodate these entries.
|
Example
QP_solver/first_qp.cpp
QP_solver/first_lp.cpp
QP_solver/first_nonnegative_qp.cpp
QP_solver/first_nonnegative_lp.cpp
QP_solver/invert_matrix.cpp
See Also
Quadratic_program_from_iterators<A_it, B_it, R_it, FL_it, L_it, FU_it, U_it, D_it, C_it>
Linear_program_from_iterators<A_it, B_it, R_it, FL_it, L_it, FU_it, U_it, C_it>
Nonnegative_quadratic_program_from_iterators<A_it, B_it, R_it, D_it, C_it>
Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it>
Quadratic_program_from_mps<NT>


![]() 0
0