CGAL::Quadratic_program_from_iterators<A_it, B_it, R_it, FL_it, L_it, FU_it, U_it, D_it, C_it>

#include <CGAL/QP_models.h>

Definition

(QP)$$	minimize$$	xTDx+cTx+c0
	subject to$$	Ax ~ b,
		l x u

in $$n real variables $$x=(x₀,...,x_n-1). Here,

• $$A is an $$m × n matrix (the constraint matrix),
• $$b is an $$m-dimensional vector (the right-hand side),
• $$ ~  is an $$m-dimensional vector of relations from $${ , =, },
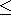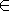
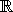
• $$l is an $$n-dimensional vector of lower bounds for $$x, where $$l_j {- 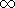} for all $$j
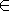
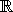
• $$u is an $$n-dimensional vector of upper bounds for $$x, where $$u_j { 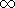} for all $$j
• $$D is a symmetric positive-semidefinite $$n × n matrix (the quadratic objective function),
• $$c is an $$n-dimensional vector (the linear objective function), and
• $$c₀ is a constant.

This class is simply a wrapper for existing iterators, and it does not copy the program data.

It frequently happens that all values in one of the vectors from above are the same, for example if the system $$Ax ~ b is actually a system of equations $$Ax=b. To get an iterator over such a vector, it is not necessary to store multiple copies of the value in some container; an instance of the class Const_oneset_iterator<T>, constructed from the value in question, does the job more efficiently.

Is Model for the Concepts

Creation

Example

QP_solver/first_qp_from_iterators.cpp

The following example for the simpler model Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it> should give you a flavor of the use of this model in practice.

QP_solver/solve_convex_hull_containment_lp.h
QP_solver/convex_hull_containment.cpp

See Also