
 |
| Π(p(w),z(w)) = ||p-z||2-wp-wz |
Four weighted points have a unique common orthogonal weighted point called the power sphere. A sphere z(w) is said to be regular if ∀ p(w) ∈ S(w), Π(p(w)-z(w)) ≥ 0.
A triangulation of S(w) is regular if the power spheres of all simplices are regular.
#include <CGAL/Regular_triangulation_3.h>
The first template argument must be a model of the RegularTriangulationTraits_3 concept.
The second template argument must be a model of the TriangulationDataStructure_3 concept. It has the default value Triangulation_data_structure_3<Triangulation_vertex_base_3<RegularTriangulationTraits_3>, Regular_triangulation_cell_base_3<RegularTriangulationTraits_3> >.
|
| ||
|
| The type for points p of weighted points p(w)=(p,wp) | |
|
| ||
|
|
||
| |||
|
Creates an empty regular triangulation, possibly specifying a traits class
traits.
| |||
|
| |||
|
Copy constructor.
| |||
|
| |||
| |||
|
Equivalent to contructing an empty triangulation with the optional
traits class argument and calling insert(first,last).
| |||
The following methods, which already exist in triangulations, are overloaded to ensure the property that all power spheres are regular.
|
|
| |
|
Inserts weighted point p in the triangulation. The optional
argument start is used as a starting place for the search. If this insertion creates a vertex, this vertex is returned. If p coincides with an existing vertex and has a greater weight, then the existing weighted point becomes hidden (see RegularTriangulationCellBase_3) and p replaces it as vertex of the triangulation. If p coincides with an already existing vertex (both point and weights being equal), then this vertex is returned and the triangulation remains unchanged. Otherwise if p does not appear as a vertex of the triangulation, then it is stored as a hidden point and this method returns the default constructed handle. | ||
|
|
| |
| Inserts weighted point p in the triangulation and returns the corresponding vertex. Similar to the above insert() function, but takes as additional parameter the return values of a previous location query. See description of Triangulation_3::locate(). | ||
The following method allows one to insert several points.
|
| ||||
|
|
| |||
Inserts the weighted points in the range [.first,
last.).
Note that this function is not garanteed to insert the points
following the order of InputIterator.
It returns the difference of the number of vertices between after and
before the insertions (it may be negative due to hidden points).
| ||||
|
|
| Removes the vertex v from the triangulation. |
Let us remark that
| Π(p(w)-z(w)) > 0 |
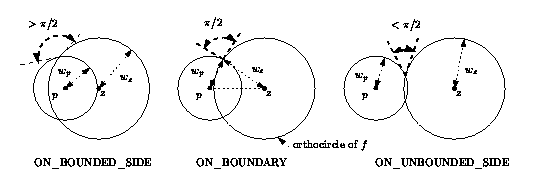
Figure 35.9: side_of_power_circle.
|
|
| |||
|
Returns the position of the weighted point p with respect to the
power sphere of c. More precisely, it returns: - ON_BOUNDED_SIDE if Π(p(w)-z(c)(w))<0 where z(c)(w) is the power sphere of c. For an infinite cell this means either that p lies strictly in the half space limited by its finite facet and not containing any other point of the triangulation, or that the angle between p and the power circle of the finite facet of c is greater than π/2. - ON_BOUNDARY if p is orthogonal to the power sphere of c i.e. Π(p(w)-z(c)(w))=0. For an infinite cell this means that p is orthogonal to the power circle of its finite facet. - ON_UNBOUNDED_SIDE if Π(p(w)-z(c)(w))>0 i.e. the angle between the weighted point p and the power sphere of c is less than π/2 or if these two spheres do not intersect. For an infinite cell this means that p does not satisfy either of the two previous conditions.
| ||||
|
|
| |||
|
Returns the position of the point p with respect to the
power circle of f. More precisely, it returns: - in dimension 3: - For a finite facet, ON_BOUNDARY if p is orthogonal to the power circle in the plane of the facet, ON_UNBOUNDED_SIDE when their angle is less than π/2, ON_BOUNDED_SIDE when it is greater than π/2 (see Figure 35.9). - For an infinite facet, it considers the plane defined by the finite facet of the cell f.first, and does the same as in dimension 2 in this plane. - in dimension 2: - For a finite facet, ON_BOUNDARY if p is orthogonal to the circle, ON_UNBOUNDED_SIDE when the angle between p and the power circle of f is less than π/2, ON_BOUNDED_SIDE when it is greater than π/2. - For an infinite facet, ON_BOUNDED_SIDE for a point in the open half plane defined by f and not containing any other point of the triangulation, ON_UNBOUNDED_SIDE in the other open half plane. If the point p is collinear with the finite edge e of f, it returns: ON_BOUNDED_SIDE if Π(p(w)-z(e)(w))<0, where z(e)(w) is the power segment of e in the line supporting e, ON_BOUNDARY if Π(p(w)-z(e)(w))=0, ON_UNBOUNDED_SIDE if Π(p(w)-z(e)(w))>0 .
| ||||
|
|
| |||
| Same as the previous method for facet i of cell c. | ||||
|
|
| |||
|
In dimension 1, returns ON_BOUNDED_SIDE if Π(p(w)-z(c)(w))<0, where z(c)(w) is the power segment of the edge represented by c, ON_BOUNDARY if Π(p(w)-z(c)(w))=0, ON_UNBOUNDED_SIDE if Π(p(w)-z(c)(w))>0 .
| ||||
|
|
| |||
Returns the vertex of the triangulation which is nearest to p
with respect to the power distance. This means that the power
of the query point p with respect to the weighted point in
the returned vertex is smaller than the power of p
with respect to the weighted point
in any other vertex. Ties are broken arbitrarily.
The default constructed
handle is returned if the triangulation is empty.
The optional argument c is a hint
specifying where to start the search.
| ||||
|
|
| |||
| Returns the vertex of the cell c that is nearest to p with respect to the power distance. | ||||
A weighted point p is said to be in conflict with a cell c in dimension 3 (resp. with a facet f in dimension 2) if it has a negative power distance to the power sphere of c (resp. to the power circle of f). The set of cells (resp. facets in dimension 2) which are in conflict with p is connected.
|
| ||||
|
| ||||
| ||||
|
Compute the conflicts with p.
The starting cell
(resp. facet) c must be in conflict with p.
Then this function returns
respectively in the output iterators: - cit: the cells (resp. facets) in conflict with p. - bfit: the facets (resp. edges) on the boundary of the conflict zone, that is, the facets (resp. edges) (t, i) where the cell (resp. facet) t is in conflict, but t->neighbor(i) is not. - ifit: the facets (resp. edges) inside the conflict zone, that facets incident to two cells (resp facets) in conflict. Returns the Triple composed of the resulting output iterators.
| ||||
|
| ||||
|
|
| |||
Similar to find_conflicts(), but reports the vertices which are on the
boundary of the conflict hole of p, in the output iterator res.
Returns the resulting output iterator.
| ||||
In the weighted setting, a face (cell, facet, edge or vertex) is said to be a Gabriel face iff the smallest sphere orthogonal to the weighted points associated to its vertices, has a positive power product with the weighted point of any other vertex of the triangulation. Any weighted Gabriel face belongs to the regular triangulation, but the reciprocal is not true. The following member functions test the Gabriel property of the faces of the regular triangulation.
|
|
| |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Note that the user should use a kernel with exact constructions in order to guarantee the computation of the Voronoi diagram (as opposed to computing the triangulation only, which requires only exact predicates).
|
|
|
Returns the weighted circumcenter of the four vertices of c.
| ||
|
|
|
Returns the dual of facet f, which is in dimension 3: either a segment, if the two cells incident to f are finite, or a ray, if one of them is infinite; in dimension 2: a point.
| ||
|
|
| same as the previous method for facet (c,i). | ||
|
| ||||
|
|
| Sends the set of duals to all the facets of rt into os. | ||
|
|
| |
|
Checks the combinatorial validity of the triangulation and the
validity of its geometric embedding (see
Section 35.1). Also checks that all the
power spheres (resp. power circles in dimension 2, power segments in
dimension 1) of cells (resp. facets in dimension 2, edges in
dimension 1) are regular. When verbose
is set to true, messages describing the first invalidity encountered
are printed. This method is mainly a debugging help for the users of advanced features. | ||