62.1 Introduction
The AABB tree component offers a static data structure and algorithms to perform efficient intersection and distance queries against sets of finite 3D geometric objects. The set of geometric objects stored in the data structure can be queried for intersection detection, intersection computation and distance. The intersection queries can be of any type, provided that the corresponding intersection predicates and constructors are implemented in the traits class. The distance queries are limited to point queries. Examples of intersection queries include line objects (rays, lines, segments) against sets of triangles, or plane objects (planes, triangles) against sets of segments. An example of a distance query consists of finding the closest point from a point query to a set of triangles.Note that this component is not suited to the problem of finding all intersecting pairs of objects. We refer to the component Box_intersection_d (Intersecting Sequences of dD Iso-oriented Boxes) which can find all intersecting pairs of iso-oriented boxes.
The AABB tree data structure takes as input an iterator range of geometric data, which is then converted into primitives. From these primitives a hierarchy of axis-aligned bounding boxes (AABBs) is constructed and used to speed up intersection and distance queries (see Figure 62.1). Each primitive gives access to both one input geometric object (so-called datum) and one reference id to this object. A typical example primitive wraps a 3D triangle as datum and a face handle of a polyhedral surface as id. Each intersection query can return the intersection objects (e.g., 3D points or segments for ray queries) as well the as id (here the face handle) of the intersected primitives. Similarly, each distance query can return the closest point from the point query as well as the id of the closest primitive.
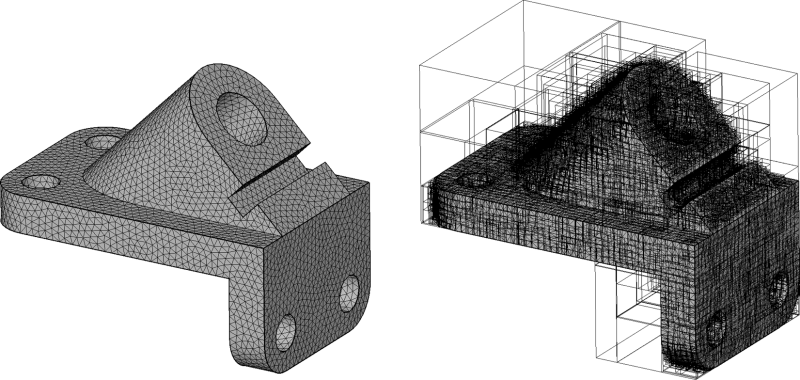
Figure 62.1: AABB tree. Left: surface triangle mesh of a mechanical part. Right: AABB tree constructed.
62.2 Interface
The main entry point to the component is the class AABB_tree which represents a static AABB tree constructed from an iterator range of geometric data. Once instantiated an AABB tree can be queried for intersection and distance queries.Intersections. Assume for example that the tree contains triangle primitives. The tree can be queried for intersection against line objects (rays, segments or line) in various ways. We distinguish intersection tests which do not construct any intersection objects, from intersections which construct the intersection objects.
Tests:
- Function do_intersect tests if the input primitives are intersected by the query. This function is fast as it involves only predicates and stops after the first encountered intersection.
- Function number_of_intersected_primitives counts all intersected primitives.
- Function all_intersected_primitives enumerates all intersected primitives ids without constructing the corresponding intersection objects.
- Function any_intersected_primitive returns the first encountered intersecting primitive id (if any) without constructing the corresponding intersection object, and stops after the first encountered intersection. Note that the traversal order of the tree is such that first herein does not refer to any particular ordering of the intersections with respect to the query.
- Function all_intersections detects and constructs all intersection objects with the input primitives.
- Function any_intersection detects and constructs the first encountered intersection and constructs the corresponding object. This function is fast as it stops after the first encountered intersection.
62.3 Examples
In all following examples the file CGAL/AABB_tree.h must be included before the kernel (here Simple_cartesian.h) so that the related intersection functions (in folder AABB_intersections) are properly parsed by the compiler.62.3.1 Tree of Triangles, for Intersection and Distance Queries
In the following example a set of 3D triangles is stored in a list. The AABB primitive wraps a triangle as datum and an iterator in the list as id. We compute the number of input triangles intersected by a ray query, as well as the closest point and the squared distance from a point query.File: examples/AABB_tree/AABB_triangle_3_example.cpp
#include <iostream>
#include <list>
#include <CGAL/AABB_tree.h> // must be inserted before kernel
#include <CGAL/AABB_traits.h>
#include <CGAL/AABB_triangle_primitive.h>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> K;
typedef K::FT FT;
typedef K::Ray_3 Ray;
typedef K::Line_3 Line;
typedef K::Point_3 Point;
typedef K::Triangle_3 Triangle;
typedef std::list<Triangle>::iterator Iterator;
typedef CGAL::AABB_triangle_primitive<K,Iterator> Primitive;
typedef CGAL::AABB_traits<K, Primitive> AABB_triangle_traits;
typedef CGAL::AABB_tree<AABB_triangle_traits> Tree;
int main()
{
Point a(1.0, 0.0, 0.0);
Point b(0.0, 1.0, 0.0);
Point c(0.0, 0.0, 1.0);
Point d(0.0, 0.0, 0.0);
std::list<Triangle> triangles;
triangles.push_back(Triangle(a,b,c));
triangles.push_back(Triangle(a,b,d));
triangles.push_back(Triangle(a,d,c));
// constructs AABB tree
Tree tree(triangles.begin(),triangles.end());
// counts #intersections
Ray ray_query(a,b);
std::cout << tree.number_of_intersected_primitives(ray_query)
<< " intersections(s) with ray query" << std::endl;
// compute closest point and squared distance
Point point_query(2.0, 2.0, 2.0);
Point closest_point = tree.closest_point(point_query);
FT sqd = tree.squared_distance(point_query);
std::cout << "squared distance: " << sqd << std::endl;
return EXIT_SUCCESS;
}
62.3.2 Tree of Polyhedron Triangle Facets for Intersection Queries
In the following example the AABB primitive wraps a facet handle of a triangle polyhedral surface as id and the corresponding 3D triangle as geometric object. From a segment query we test the intersections, then compute the number of intersections, compute the first encountered intersection (generally a point), compute all intersections (where each intersection is a pair of one CGAL object and one primitive id - here a face handle) and compute all intersected primitives. The latter involves only tests and no predicates and is hence faster than computing all intersections. We also compute the first encountered intersection with a plane query, which is generally a segment.File: examples/AABB_tree/AABB_polyhedron_facet_intersection_example.cpp
#include <iostream>
#include <CGAL/AABB_tree.h> // must be inserted before kernel
#include <CGAL/AABB_traits.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/AABB_polyhedron_triangle_primitive.h>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> K;
typedef K::Point_3 Point;
typedef K::Plane_3 Plane;
typedef K::Vector_3 Vector;
typedef K::Segment_3 Segment;
typedef CGAL::Polyhedron_3<K> Polyhedron;
typedef CGAL::AABB_polyhedron_triangle_primitive<K,Polyhedron> Primitive;
typedef CGAL::AABB_traits<K, Primitive> Traits;
typedef CGAL::AABB_tree<Traits> Tree;
typedef Tree::Object_and_primitive_id Object_and_primitive_id;
typedef Tree::Primitive_id Primitive_id;
int main()
{
Point p(1.0, 0.0, 0.0);
Point q(0.0, 1.0, 0.0);
Point r(0.0, 0.0, 1.0);
Point s(0.0, 0.0, 0.0);
Polyhedron polyhedron;
polyhedron.make_tetrahedron(p, q, r, s);
// constructs AABB tree
Tree tree(polyhedron.facets_begin(),polyhedron.facets_end());
// constructs segment query
Point a(-0.2, 0.2, -0.2);
Point b(1.3, 0.2, 1.3);
Segment segment_query(a,b);
// tests intersections with segment query
if(tree.do_intersect(segment_query))
std::cout << "intersection(s)" << std::endl;
else
std::cout << "no intersection" << std::endl;
// computes #intersections with segment query
std::cout << tree.number_of_intersected_primitives(segment_query)
<< " intersection(s)" << std::endl;
// computes first encountered intersection with segment query
// (generally a point)
boost::optional<Object_and_primitive_id> intersection =
tree.any_intersection(segment_query);
if(intersection)
{
// gets intersection object
Object_and_primitive_id op = *intersection;
CGAL::Object object = op.first;
Point point;
if(CGAL::assign(point,object))
std::cout << "intersection object is a point" << std::endl;
}
// computes all intersections with segment query (as pairs object - primitive_id)
std::list<Object_and_primitive_id> intersections;
tree.all_intersections(segment_query, std::back_inserter(intersections));
// computes all intersected primitives with segment query as primitive ids
std::list<Primitive_id> primitives;
tree.all_intersected_primitives(segment_query, std::back_inserter(primitives));
// constructs plane query
Vector vec(0.0,0.0,1.0);
Plane plane_query(a,vec);
// computes first encountered intersection with plane query
// (generally a segment)
intersection = tree.any_intersection(plane_query);
if(intersection)
{
// gets intersection object
Object_and_primitive_id op = *intersection;
CGAL::Object object = op.first;
Segment segment;
if(CGAL::assign(segment,object))
std::cout << "intersection object is a segment" << std::endl;
}
return EXIT_SUCCESS;
}
62.3.3 Tree of Polyhedron Triangle Facets for Distance Queries
In the following example the AABB primitive wraps a facet handle of a triangle polyhedral surface as id and the corresponding 3D triangle as geometric object. From a point query we compute the squared distance, the closest point as well as the closest point and primitive id. The latter returns a pair composed of a point and a face handle.File: examples/AABB_tree/AABB_polyhedron_facet_distance_example.cpp
#include <iostream>
#include <CGAL/AABB_tree.h> // must be inserted before kernel
#include <CGAL/AABB_traits.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/AABB_polyhedron_triangle_primitive.h>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> K;
typedef K::FT FT;
typedef K::Point_3 Point;
typedef K::Segment_3 Segment;
typedef CGAL::Polyhedron_3<K> Polyhedron;
typedef CGAL::AABB_polyhedron_triangle_primitive<K,Polyhedron> Primitive;
typedef CGAL::AABB_traits<K, Primitive> Traits;
typedef CGAL::AABB_tree<Traits> Tree;
typedef Tree::Object_and_primitive_id Object_and_primitive_id;
typedef Tree::Point_and_primitive_id Point_and_primitive_id;
int main()
{
Point p(1.0, 0.0, 0.0);
Point q(0.0, 1.0, 0.0);
Point r(0.0, 0.0, 1.0);
Point s(0.0, 0.0, 0.0);
Polyhedron polyhedron;
polyhedron.make_tetrahedron(p, q, r, s);
// constructs AABB tree and computes internal KD-tree
// data structure to accelerate distance queries
Tree tree(polyhedron.facets_begin(),polyhedron.facets_end());
tree.accelerate_distance_queries();
// query point
Point query(0.0, 0.0, 3.0);
// computes squared distance from query
FT sqd = tree.squared_distance(query);
std::cout << "squared distance: " << sqd << std::endl;
// computes closest point
Point closest = tree.closest_point(query);
std::cout << "closest point: " << closest << std::endl;
// computes closest point and primitive id
Point_and_primitive_id pp = tree.closest_point_and_primitive(query);
std::cout << "closest point: " << pp.first << std::endl;
Polyhedron::Face_handle f = pp.second; // closest primitive id
return EXIT_SUCCESS;
}
62.3.4 Tree of Segments for Intersection and Distance Queries
In the following example the segments are stored into a list, and the AABB primitive wraps a segment as datum and an iterator in the list as id. We compute the number of intersections with plane and triangles queries, and the closest point from a point query.File: examples/AABB_tree/AABB_segment_3_example.cpp
#include <iostream>
#include <list>
#include <CGAL/AABB_tree.h> // must be inserted before kernel
#include <CGAL/AABB_traits.h>
#include <CGAL/AABB_segment_primitive.h>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> K;
typedef K::FT FT;
typedef K::Point_3 Point;
typedef K::Plane_3 Plane;
typedef K::Segment_3 Segment;
typedef K::Triangle_3 Triangle;
typedef std::list<Segment>::iterator Iterator;
typedef CGAL::AABB_segment_primitive<K,Iterator> Primitive;
typedef CGAL::AABB_traits<K, Primitive> Traits;
typedef CGAL::AABB_tree<Traits> Tree;
int main()
{
Point a(1.0, 0.0, 0.0);
Point b(0.0, 1.0, 0.0);
Point c(0.0, 0.0, 1.0);
Point d(0.0, 0.0, 0.0);
std::list<Segment> segments;
segments.push_back(Segment(a,b));
segments.push_back(Segment(a,c));
segments.push_back(Segment(c,d));
// constructs the AABB tree and the internal search tree for
// efficient distance computations.
Tree tree(segments.begin(),segments.end());
tree.accelerate_distance_queries();
// counts #intersections with a plane query
Plane plane_query(a,b,d);
std::cout << tree.number_of_intersected_primitives(plane_query)
<< " intersections(s) with plane" << std::endl;
// counts #intersections with a triangle query
Triangle triangle_query(a,b,c);
std::cout << tree.number_of_intersected_primitives(triangle_query)
<< " intersections(s) with triangle" << std::endl;
// computes the closest point from a point query
Point point_query(2.0, 2.0, 2.0);
Point closest = tree.closest_point(point_query);
return EXIT_SUCCESS;
}
62.3.5 Tree of Polyhedron Edge Segments for Intersection and Distance Queries
In the following example the AABB primitive wraps a halfedge handle as id and generates a 3D segment on the fly, each time its method datum is called. We compute the number of intersections with a triangle query and the closest point from a point query.File: examples/AABB_tree/AABB_polyhedron_edge_example.cpp
#include <iostream>
#include <CGAL/AABB_tree.h> // must be inserted before kernel
#include <CGAL/AABB_traits.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/AABB_polyhedron_segment_primitive.h>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> K;
typedef K::FT FT;
typedef K::Point_3 Point;
typedef K::Triangle_3 Triangle;
typedef CGAL::Polyhedron_3<K> Polyhedron;
typedef CGAL::AABB_polyhedron_segment_primitive<K,Polyhedron> Primitive;
typedef CGAL::AABB_traits<K, Primitive> Traits;
typedef CGAL::AABB_tree<Traits> Tree;
int main()
{
Point p(1.0, 0.0, 0.0);
Point q(0.0, 1.0, 0.0);
Point r(0.0, 0.0, 1.0);
Point s(0.0, 0.0, 0.0);
Polyhedron polyhedron;
polyhedron.make_tetrahedron(p, q, r, s);
// constructs the AABB tree and the internal search tree for
// efficient distance queries.
Tree tree(polyhedron.edges_begin(),polyhedron.edges_end());
tree.accelerate_distance_queries();
// counts #intersections with a triangle query
Triangle triangle_query(p,q,r);
std::cout << tree.number_of_intersected_primitives(triangle_query)
<< " intersections(s) with triangle" << std::endl;
// computes the closest point from a query point
Point point_query(2.0, 2.0, 2.0);
Point closest = tree.closest_point(point_query);
return EXIT_SUCCESS;
}
62.3.6 Trees of Custom Primitives
The AABB tree example folder contains three examples of trees constructed with customize primitives. In AABB_custom_example.cpp the primitive contains triangles which are defined by three pointers to custom points. In AABB_custom_triangle_soup_example.cpp all input triangles are stored into a single array so as to form a triangle soup. The primitive internally uses a boost::iterator_adaptor so as to provide the three functions (id(), datum(), reference_point()) required by the primitive concept. In AABB_custom_indexed_triangle_set_example.cpp the input is an indexed triangle set stored through two arrays: one array of points and one array of indices which refer to the point array. Here also the primitive internally uses a boost::iterator_adaptor.62.4 Performances
We provide some performance numbers for the case where the AABB tree contains a set of polyhedron triangle facets. We measure the tree construction time, the memory occupancy and the number of queries per second for a variety of intersection and distance queries. The machine used is a PC running Windows XP64 with an Intel CPU Core2 Extreme clocked at 3.06 GHz with 4GB of RAM. By default the kernel used is Simple_cartesian<double> (the fastest in our experiments). The program has been compiled with Visual C++ 2005 compiler with the O2 option which maximizes speed.
62.4.1 Construction
The surface triangle mesh chosen for benchmarking the tree construction is the knot model (14,400 triangles) depicted by Figure 62.4.3. We measure the tree construction time (both AABB tree alone and AABB tree with internal KD-tree) for this model as well as for three denser versions subdivided through the Loop subdivision scheme which multiplies the number of triangles by four.
| Number of triangles | Construction (in ms) | Construction with internal KD-tree (in ms) |
| 14,400 | 156 | 157 |
| 57,600 | 328 | 328 |
| 230,400 | 1,141 | 1,437 |
| 921,600 | 4,813 | 5,953 |
62.4.2 Memory
When using the polyhedron triangle facet primitive (defined in AABB_polyhedron_triangle_primitive.h) the AABB tree occupies approximately 61 bytes per primitive (without constructing the internal KD-tree). It increases to approximately 150 bytes per primitive when constructing the internal KD-tree with one reference point per primitive (the default mode when calling the function tree.accelerate_distance_queries()). Note that the polyhedron facet primitive primitive stores only one facet handle as primitive id and computes on the fly a 3D triangle from the facet handle stored internally. When explicitly storing a 3D triangle in the primitive the tree occupies approximately 140 bytes per primitive instead of 60 (without constructing the internal KD-tree).
The following table provides orders of memory occupancy in MBytes for an increasing number of triangles. As the internal KD-tree used to accelerate the distance queries dominates the memory occupancy, we recommend to specify for large models a lower number of reference point (evenly distributed) to construct the internal KD-tree through the function tree.accelerate_distance_queries(begin,end) which takes an iterator range as input.
| Number of triangles | AABB tree (in MBytes) | AABB tree with internal KD-tree (in MBytes) |
| 18,400 | 1.10 | 2.76 |
| 102,400 | 6.33 | 14.73 |
| 1,022,400 | 59.56 | 151.31 |
| 1,822,400 | 108.34 | 291.84 |
62.4.3 Intersections
The following table measures the number of intersection queries per second on the 14,400 triangle version of the knot mesh model for ray, line, segment and plane queries. Each ray query is generated by choosing a random source point within the mesh bounding box and a random vector. A line or segment query is generated by choosing two random points inside the bounding box. A plane query is generated by picking a random point inside the bounding box and a random normal vector. Note that a plane query generally intersects many triangles of the input surface mesh. This explains the low performance numbers for the intersection functions which enumerate all intersections.
| Function | Segment | Ray | Line | Plane |
| do_intersect() | 187,868 | 185,649 | 206,096 | 377,969 |
| any_intersected_primitive() | 190,684 | 190,027 | 208,941 | 360,337 |
| any_intersection() | 147,468 | 143,230 | 148,235 | 229,336 |
| number_of_intersected_primitives() | 64,389 | 52,943 | 54,559 | 7,906 |
| all_intersected_primitives() | 65,553 | 54,838 | 53,183 | 5,693 |
| all_intersections() | 46,507 | 38,471 | 36,374 | 2,644 |
Curve 62.4.3 plots the number of queries per second (here the all_intersections function with random segment queries) against the number of input triangles for the knot triangle surface mesh.
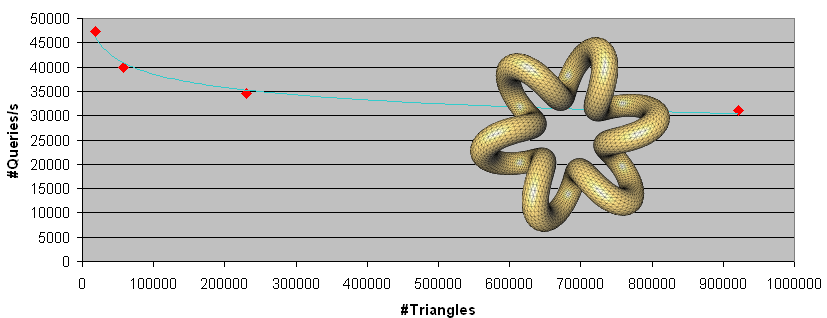
Figure 62.2: Number of queries per second against number of triangles for the knot model with 14K (shown), 57K, 230K and 921K triangles. We call the all_intersections function with segment queries randomly chosen within the bounding box.
The following table measures the number of all_intersections() queries per second against several kernels. We use the 14,400 triangle version of the knot mesh model for random segment queries. Note how the Simple_cartesian kernel is substantially faster than the Cartesian kernel.
| Kernel | Queries/s (all_intersections() with segment queries) |
| Simple_cartesian<double> | 46,507 |
| Simple_cartesian<float> | 43,187 |
| Cartesian<double> | 5,335 |
| Cartesian<float> | 5,522 |
| Exact_predicates_inexact_constructions | 18,411 |
62.4.4 Distances
The surface triangle mesh chosen for benchmarking distances is again the knot model in four increasing resolutions obtained through Loop subdivision. In the following table we first measure the tree construction time (which includes the construction of the internal KD-tree data structure used to accelerate the distance queries by up to one order of magnitude in our experiments). We then measure the number of queries per second for the three types distance queries (closest_point, squared_distance and closest_point_and_primitive) from point queries randomly chosen inside the bounding box.
| Nb triangles | Construction (ms) | Closest_point() | squared_distance() | closest_point_and_primitive() |
| 14,400 | 157 | 45,132 | 45,626 | 45,770 |
| 57,600 | 328 | 21,589 | 21,312 | 21,137 |
| 230,400 | 1,437 | 11,063 | 10,962 | 11,086 |
| 921,600 | 5,953 | 5,636 | 5,722 | 5,703 |
62.4.5 Summary
The experiments described above are neither exhaustive nor conclusive as we have chosen one specific case where the input primitives are the facets of a triangle surface polyhedron. Nevertheless we now provide some general observations and advices about how to put the AABB tree to use with satisfactory performances. While the tree construction times and memory occupancy do not fluctuate much in our experiments depending on the input surface triangle mesh, the performance expressed in number of queries varies greatly depending on a complex combination of criteria: type of kernel, number of input primitives, distribution of primitives in space, type of function queried, type of query and location of query in space.
- Kernel: The type of CGAL kernel turns out to dominate the final execution times, the maximum performances being obtained with the simple Cartesian kernel parameterized with the double precision number type. In applications where the intersection and distance execution times are crucial it is possible to use this kernel for the AABB tree in combination with a more robust kernel for the main data structure.
- Primitives: Although the number of input primitives plays an obvious role in the final performance, their distribution in space is at least equally important in order to obtain a well-balanced AABB tree. Ideally the primitives must be evenly distributed in space and the long primitives spanning the bounding box of the tree root node must be avoided as much as possible. It is often beneficial to split these long primitives into smaller ones before constructing the tree, e.g., through recursive longest edge bisection for triangle surface meshes.
- Function: The type of function queried plays another important role. Obviously the ``exhaustive'' functions, which list all intersections, are slower than the ones stopping after the first intersection. Within each of these functions the ones which call only intersection tests (do_intersect(), number_of_intersected_primitives(), any_intersected_primitive(), all_intersected_primitives()) are faster than the ones which explicitly construct the intersections (any_intersection() and all_intersections()).
- Query: The type of query (e.g., line, ray, segment or plane used above) plays another role, strongly correlated with the type of function (exhaustive or not, and whether or not it constructs the intersections). When all intersection constructions are needed, the final execution times highly depend on the complexity of the general intersection object. For example a plane query generally intersects a surface triangle mesh into many segments while a segment query generally intersects a surface triangle mesh into few points. Finally, the location of the query in space also plays an obvious role in the performances, especially for the distance queries. Assuming the internal KD-tree constructed through the function tree.accelerate_distance_queries(), it is preferable to specify a query point already close to the surface triangle mesh so that the query traverses only few AABBs of the tree. For a large number of primitive data (greater than 2M faces in our experiments) however we noticed that it is not necessary (and sometimes even slower) to use all reference points when constructing the KD-tree. In these cases we recommend to specify trough the function tree.accelerate_distance_queries(begin,end) fewer reference points (typically not more than 100K) evenly distributed over the input primitives.
62.5 Implementation Details
The AABB tree construction is initialized by computing the AABB of the whole set of input primitives. All primitives are then sorted along the longest coordinate axis of this box, and the primitives are separated into two equal size sets. This procedure is applied recursively until an AABB contains a single primitive. The tree is leafless as presented in opcode [Ter05]. An intersection query traverses the tree by computing intersection tests only with respect to the AABBs during traversal, and with respect to the input primitives at the end of traversal (in the leafs of the tree).The reference id is not used internally but simply used by the AABB tree to refer to the primitive in the results provided to the user. It follows that, while in most cases each reference id corresponds to a unique primitive, this is not a requirement of the component. This way a user may use these reference ids as labels, each of them being shared by several geometric object.
A distance query between a query point q and the input primitives is turned into a ball query centered at q. The ball traverses the tree while recursively querying intersections with the AABBs, and computes the closest point p from the query point to the input primitives at the leafs of the tree. The ball radius is then shrunk to the distance between p and q for all remaining recursive traversals of the tree. Efficiency is achieved through setting the initial ball radius to a small value still guaranteed to intersect the input primitives. This is achieved by constructing through the function accelerate_distance_queries an internal secondary data structure which provides a good hint to the algorithm at the beginning of the traversal.
62.6 Design and Implementation History
Camille Wormser and Pierre Alliez started working on a data structure for efficient collision detection in 2007. The generic design for implementing both intersection and distance queries, and for generic queries and primitives was developed by Camille Wormser. In 2009, Pierre Alliez, Stéphane Tayeb and Camille Wormser made the implementation CGAL-compliant, with the help of Laurent Rineau for optimizing the tree construction. The authors wish to thank Andreas Fabri, Jane Tournois, Mariette Yvinec and Sylvain Lefèbvre for helpful comments and discussions.