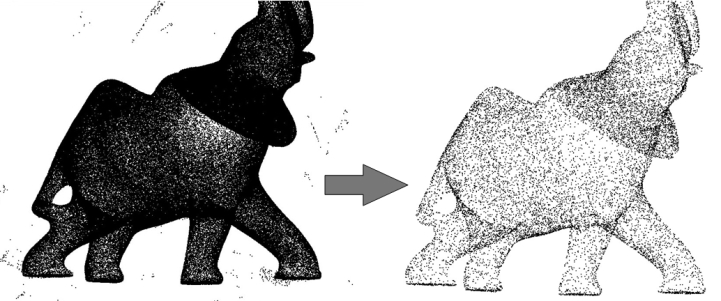
Figure 58.1: Point set processing. Left: 275K points sampled on the statue of an elephant with a Minolta laser scanner. Right: point set after clean-up and simplification to 17K points.
Pierre Alliez, Laurent Saboret, Nader Salman
This Cgal component implements methods to analyze and process unorganized 3D point sets. The input is an unorganized 3D point set, possibly with normal attributes (unoriented or oriented). This point set can be analyzed to measure geometric properties such as average spacing between the points and their K nearest neighbors. It can be processed with functions devoted to the simplification, outlier removal, smoothing, normal estimation and normal orientation. The processing of point sets is often needed in applications dealing with measurement data, such as surface reconstruction from laser scanned data (see Figure 58.1).

Figure 58.1: Point set processing. Left: 275K points sampled on the statue of an elephant with a Minolta laser scanner. Right: point set after clean-up and simplification to 17K points.
In the context of surface reconstruction we can position the elements of this component along the common surface reconstruction pipeline (Figure 58.2) which involves the following steps: 1) Scanning and scan alignment to produce a set of points or points with normals (alignment is not yet covered in Cgal); 2) Outlier removal; 3) Simplification to reduce the number of input points; 4) Smoothing to reduce noise in the input data; 5) Normal estimation and orientation when the normals are not already provided by the acquisition device; and 6) Surface reconstruction. Chapter Surface_reconstruction_points_3 49 deals with surface reconstruction from point sets with normal attributes.
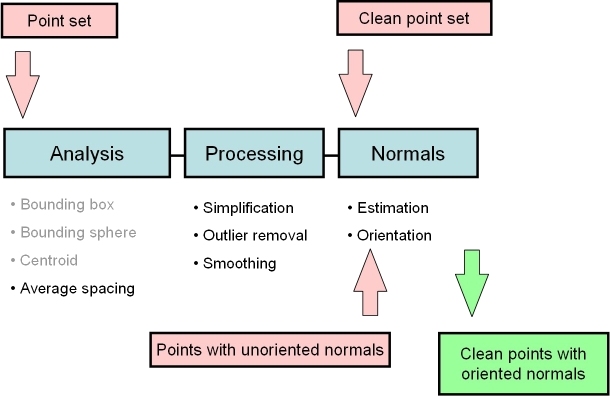
Figure 58.2: Point set processing pipeline for surface reconstruction. The algorithms listed in gray are available from other Cgal components (bounding volumes and principal component analysis).
File: examples/Point_set_processing_3/read_write_xyz_point_set_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <utility> // defines std::pair
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored as a std::pair.
typedef std::pair<Point, Vector> Pwn;
int main(void)
{
// Reads a .xyz point set file in points[].
// Note: read_xyz_points_and_normals() requires an output iterator
// over points and as well as property maps to access each
// point position and normal.
std::vector<Pwn> points;
std::ifstream in("data/oni.xyz");
if (!in ||
!CGAL::read_xyz_points_and_normals(
in,std::back_inserter(points),
CGAL::First_of_pair_property_map<Pwn>(),
CGAL::Second_of_pair_property_map<Pwn>()))
{
std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
return EXIT_FAILURE;
}
// Saves point set.
// Note: write_xyz_points_and_normals() requires an output iterator
// over points as well as property maps to access each
// point position and normal.
std::ofstream out("oni_copy.xyz");
if (!out ||
!CGAL::write_xyz_points_and_normals(
out, points.begin(), points.end(),
CGAL::First_of_pair_property_map<Pwn>(),
CGAL::Second_of_pair_property_map<Pwn>()))
{
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}
The following example reads a point set in the xyz format and computes the average spacing. Index, position and color are stored in a tuple and accessed through property maps.
File: examples/Point_set_processing_3/average_spacing_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/compute_average_spacing.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
#include <boost/tuple/tuple.hpp>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_3 Point;
// Data type := index, followed by the point, followed by three integers that
// define the Red Green Blue color of the point.
typedef boost::tuple<int, Point, int, int, int> IndexedPointWithColorTuple;
int main(void)
{
// Reads a .xyz point set file in points.
// As the point is the second element of the tuple (that is with index 1)
// we use a property map that accesses the 1st element of the tuple.
std::vector<IndexedPointWithColorTuple> points;
std::ifstream stream("data/sphere_20k.xyz");
if (!stream ||
!CGAL::read_xyz_points(
stream, std::back_inserter(points),
CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>()))
{
std::cerr << "Error: cannot read file data/sphere_20k.xyz" << std::endl;
return EXIT_FAILURE;
}
// Initialize index and RGB color fields in tuple.
// As the index and RGB color are respectively the first and third-fifth elements
// of the tuple we use a get function from the property map that accesses the 0
// and 2-4th elements of the tuple.
for(unsigned int i = 0; i < points.size(); i++)
{
points[i].get<0>() = i; // set index value of tuple to i
points[i].get<2>() = 0; // set RGB color to black
points[i].get<3>() = 0;
points[i].get<4>() = 0;
}
// Computes average spacing.
const unsigned int nb_neighbors = 6; // 1 ring
FT average_spacing = CGAL::compute_average_spacing(
points.begin(), points.end(),
CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>(),
nb_neighbors);
std::cout << "Average spacing: " << average_spacing << std::endl;
return EXIT_SUCCESS;
}
Note that other functions such as centroid or bounding volumes are found in other Cgal components:The following example reads a point set and removes 5% of the points. It uses the CGAL::Dereference_property_map<Point_3> property map (optional as it is the default position property map of all functions in this component.)
File: examples/Point_set_processing_3/remove_outliers_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/remove_outliers.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(void)
{
// Reads a .xyz point set file in points[].
// The Dereference_property_map property map can be omitted here as it is the default value.
std::vector<Point> points;
std::ifstream stream("data/oni.xyz");
if (!stream ||
!CGAL::read_xyz_points(stream, std::back_inserter(points),
CGAL::Dereference_property_map<Point>()))
{
std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
return EXIT_FAILURE;
}
// Removes outliers using erase-remove idiom.
// The Dereference_property_map property map can be omitted here as it is the default value.
const double removed_percentage = 5.0; // percentage of points to remove
const int nb_neighbors = 24; // considers 24 nearest neighbor points
points.erase(CGAL::remove_outliers(points.begin(), points.end(),
CGAL::Dereference_property_map<Point>(),
nb_neighbors, removed_percentage),
points.end());
// Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
std::vector<Point>(points).swap(points);
return EXIT_SUCCESS;
}
The following example reads a point set and simplifies it by clustering.
File: examples/Point_set_processing_3/grid_simplification_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/grid_simplify_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(void)
{
// Reads a .xyz point set file in points[].
std::vector<Point> points;
std::ifstream stream("data/oni.xyz");
if (!stream ||
!CGAL::read_xyz_points(stream, std::back_inserter(points)))
{
std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
return EXIT_FAILURE;
}
// simplification by clustering using erase-remove idiom
double cell_size = 0.001;
points.erase(CGAL::grid_simplify_point_set(points.begin(), points.end(), cell_size),
points.end());
// Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
std::vector<Point>(points).swap(points);
return EXIT_SUCCESS;
}

Figure 58.3: Point set simplification through grid-based clustering. Removed points are depicted in red. Notice how low-density areas (in green) are not simplified.
The following example generates a set of 9 points close to the xy plane and smooths them using 8 nearest neighbors:
File: examples/Point_set_processing_3/jet_smoothing_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/jet_smooth_point_set.h>
#include <vector>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(void)
{
// generate point set
std::vector<Point> points;
points.push_back(Point( 0.0, 0.0, 0.001));
points.push_back(Point(-0.1,-0.1, 0.002));
points.push_back(Point(-0.1,-0.2, 0.001));
points.push_back(Point(-0.1, 0.1, 0.002));
points.push_back(Point( 0.1,-0.1, 0.000));
points.push_back(Point( 0.1, 0.2, 0.001));
points.push_back(Point( 0.2, 0.0, 0.002));
points.push_back(Point( 0.2, 0.1, 0.000));
points.push_back(Point( 0.0,-0.1, 0.001));
// Smoothing.
const unsigned int nb_neighbors = 8; // default is 24 for real-life point sets
CGAL::jet_smooth_point_set(points.begin(), points.end(), nb_neighbors);
return EXIT_SUCCESS;
}
Assuming a point set sampled over an inferred surface S, two functions provide an estimate of the normal to S at each point. The result is an unoriented normal vector for each input point.
Function CGAL::jet_estimate_normals() estimates the normal direction at each point from the input set by fitting a jet surface over its k nearest neighbors. The default jet is a quadric surface. This algorithm is well suited to point sets scattered over curved surfaces.
Function CGAL::pca_estimate_normals() estimates the normal direction at each point from the set by linear least squares fitting of a plane over its k nearest neighbors. This algorithm is simpler and faster than CGAL::jet_estimate_normals().
Function CGAL::mst_orient_normals() orients the normals of a set of points with unoriented normals using the method described by Hoppe et al. in Surface reconstruction from unorganized points [HDD+92]. More specifically, this method constructs a Riemannian graph over the input points (the graph of the K nearest neighbor points) and propagates a seed normal orientation within a minimum spanning tree computed over this graph. The result is an oriented normal vector for each input unoriented normal, except for the normals which could not be successfully oriented.
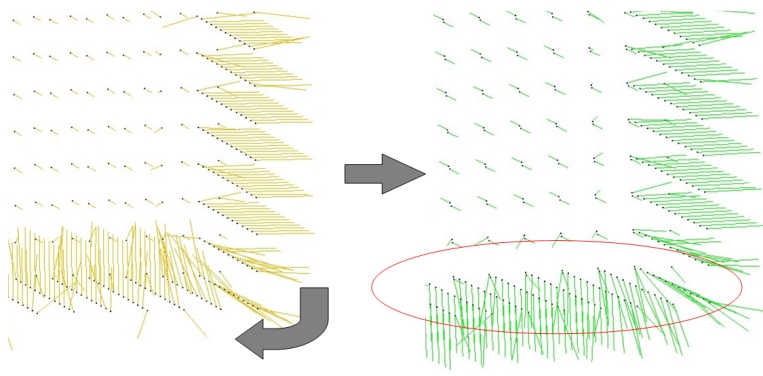
Figure 58.4: Normal orientation of a sampled cube surface. Left: unoriented normals. Right: orientation of right face normals is propagated to bottom face.
The following example reads a point set from a file, estimates the normals through PCA over the 6 nearest neighbors and orients the normals:
File: examples/Point_set_processing_3/normals_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/pca_estimate_normals.h>
#include <CGAL/mst_orient_normals.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <utility> // defines std::pair
#include <list>
#include <fstream>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;
int main(void)
{
// Reads a .xyz point set file in points[].
std::list<PointVectorPair> points;
std::ifstream stream("data/sphere_20k.xyz");
if (!stream ||
!CGAL::read_xyz_points(stream,
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>()))
{
std::cerr << "Error: cannot read file data/sphere_20k.xyz" << std::endl;
return EXIT_FAILURE;
}
// Estimates normals direction.
// Note: pca_estimate_normals() requires an iterator over points
// as well as property maps to access each point's position and normal.
const int nb_neighbors = 18; // K-nearest neighbors = 3 rings
CGAL::pca_estimate_normals(points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
nb_neighbors);
// Orients normals.
// Note: mst_orient_normals() requires an iterator over points
// as well as property maps to access each point's position and normal.
std::list<PointVectorPair>::iterator unoriented_points_begin =
CGAL::mst_orient_normals(points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
nb_neighbors);
// Optional: delete points with an unoriented normal
// if you plan to call a reconstruction algorithm that expects oriented normals.
points.erase(unoriented_points_begin, points.end());
// Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
std::list<PointVectorPair>(points).swap(points);
return EXIT_SUCCESS;
}