|
CGAL 5.1 - Manual
|
|
CGAL 5.1 - Manual
|
Surface reconstruction from point clouds is a core topic in geometry processing [3]. It is an ill-posed problem: there is an infinite number of surfaces that approximate a single point cloud and a point cloud does not define a surface in itself. Thus additional assumptions and constraints must be defined by the user and reconstruction can be achieved in many different ways. This tutorial provides guidance on how to use the different algorithms of CGAL to effectively perform surface reconstruction.
CGAL offers three different algorithms for surface reconstruction:
Because reconstruction is an ill-posed problem, it must be regularized via prior knowledge. Differences in prior lead to different algorithms, and choosing one or the other of these methods is dependent on these priors. For example, Poisson always generates closed shapes (bounding a volume) and requires normals but does not interpolate input points (the output surface does not pass exactly through the input points). The following table lists different properties of the input and output to help the user choose the method best suited to each problem:
| Poisson | Advancing front | Scale space | |
|---|---|---|---|
| Are normals required? | Yes | No | No |
| Is noise handled? | Yes | By preprocessing | Yes |
| Is variable sampling handled? | Yes | Yes | By preprocessing |
| Are input points exactly on the surface? | No | Yes | Yes |
| Is the output always closed? | Yes | No | No |
| Is the output always smooth? | Yes | No | No |
| Is the output always manifold? | Yes | Yes | Optional |
| Is the output always orientable? | Yes | Yes | Optional |
More information on these different methods can be found on their respective manual pages and in Section Reconstruction.
This tutorial aims at providing a more comprehensive view of the possibilities offered by CGAL for dealing with point clouds, for surface reconstruction purposes. The following diagram shows an overview (not exhaustive) of common reconstruction steps using CGAL tools.
We now review some of these steps in more detail.
The reconstruction algorithms in CGAL take a range of iterators on a container as input and use property maps to access the points (and the normals when they are required). Points are typically stored in plain text format (denoted as 'XYZ' format) where each point is separated by a newline character and each coordinate separated by a white space. Other formats available are 'OFF', 'PLY' and 'LAS'. CGAL provides functions to read such formats:
read_xyz_points()read_off_points()read_ply_points()read_ply_points_with_properties() to read additional PLY propertiesread_las_points()read_las_points_with_properties() to read additional LAS propertiesCGAL also provides a dedicated container CGAL::Point_set_3 to handle point sets with additional properties such as normal vectors. In this case, property maps are easily handled as shown in the following sections. This structure also handles the stream operator to read point sets in any of the formats previously described. Using this method yields substantially shorter code, as can be seen on the following example:
Because reconstruction algorithms have some specific requirements that point clouds do not always meet, some preprocessing might be necessary to yield the best results.
Note that this preprocessing step is optional: when the input point cloud has no imperfections, reconstruction can be applied to it without any preprocessing.
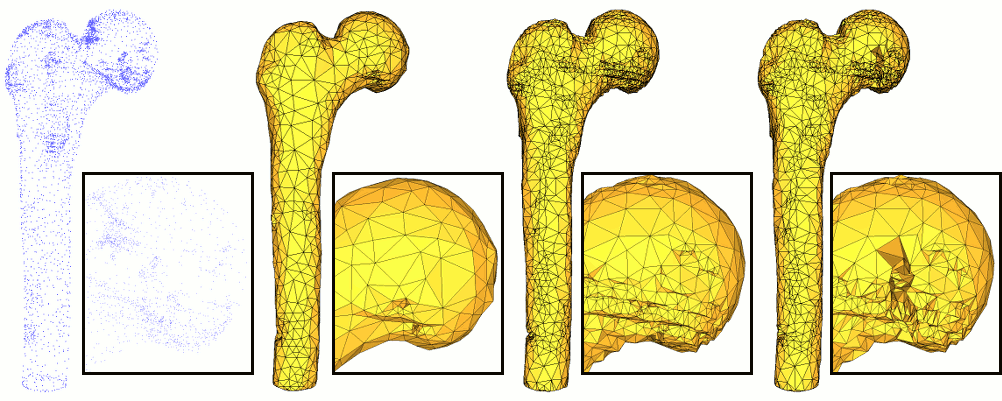
Some acquisition techniques generate points which are far away from the surface. These points, commonly referred to as "outliers", have no relevance for reconstruction. Using the CGAL reconstruction algorithms on outlier-ridden point clouds produce overly distorted output, it is therefore strongly advised to filter these outliers before performing reconstruction.
Some laser scanners generate points with widely variable sampling. Typically, lines of scan are very densely sampled but the gap between two lines of scan is much larger, leading to an overly massive point cloud with large variations of sampling density. This type of input point cloud might generate imperfect output using algorithms which, in general, only handle small variations of sampling density.
CGAL provides several simplification algorithms. In addition to reducing the size of the input point cloud and therefore decreasing computation time, some of them can help making the input more uniform. This is the case of the function grid_simplify_point_set() which defines a grid of a user-specified size and keeps one point per occupied cell.
Although reconstructions via 'Poisson' or 'Scale space' handle noise internally, one may want to get tighter control over the smoothing step. For example, a slightly noisy point cloud can benefit from some reliable smoothing algorithms and be reconstructed via 'Advancing front' which provides relevant properties (oriented mesh with boundaries).
Two functions are provided to smooth a noisy point cloud with a good approximation (i.e. without degrading curvature, for example):
These functions directly modify the container:
Poisson Surface Reconstruction requires points with oriented normal vectors. To apply the algorithm to a raw point cloud, normals must be estimated first, for example with one of these two functions:
PCA is faster but jet is more accurate in the presence of high curvatures. These function only estimates the direction of the normals, not their orientation (the orientation of the vectors might not be locally consistent). To properly orient the normals, the function mst_orient_normals() can be used. Notice that it can also be used directly on input normals if their orientation is not consistent.
Poisson reconstruction consists in computing an implicit function whose gradient matches the input normal vector field: this indicator function has opposite signs inside and outside of the inferred shape (hence the need for closed shapes). This method thus requires normals and produces smooth closed surfaces. It is not appropriate if the surface is expected to interpolate the input points. On the contrary, it performs well if the aim is to approximate a noisy point cloud with a smooth surface.
Advancing front is a Delaunay-based approach which interpolates a subset of the input points. It generates triples of point indices which describe the triangular facets of the reconstruction: it uses a priority queue to sequentially pick the Delaunay facet the most likely to be part of the surface, based on a size criterion (to favor the small facets) and an angle criterion (to favor smoothness). Its main virtue is to generate oriented manifold surfaces with boundaries: contrary to Poisson, it does not require normals and is not bound to reconstruct closed shapes. However, it requires preprocessing if the point cloud is noisy.
The Advancing Front package provides several ways of constructing the function. Here is a simple example:
Scale space reconstruction aims at producing a surface which interpolates the input points (interpolant) while offering some robustness to noise. More specifically, it first applies several times a smoothing filter (such as Jet Smoothing) to the input point set to produce a scale space; then, the smoothest scale is meshed (using for example the Advancing Front mesher); finally, the resulting connectivity between smoothed points is propagated to the original raw input point set. This method is the right choice if the input point cloud is noisy but the user still wants the surface to pass exactly through the points.
Each of these methods produce a triangle mesh stored in different ways. If this output mesh is hampered by defects such as holes or self-intersections, CGAL provide several algorithms to post-process it (hole filling, remeshing, etc.) in the package Polygon Mesh Processing.
We do not discuss these functions here as there are many postprocessing possibilities whose relevance strongly depends on the user's expectations on the output mesh.
The mesh (postprocessed or not) can easily be saved in the PLY format (here, using the binary variant):
A polygon soup can also be saved in the OFF format by iterating on the points and faces:
Finally, if the polygon soup can be converted into a polygon mesh, it can also be saved directly in the OFF format using the stream operator:
All the code snippets used in this tutorial can be assembled to create a full algorithm pipeline (provided the correct includes are used). We give a full code example which achieves all the steps described in this tutorial. The reconstruction method can be selected by the user at runtime with the second argument.
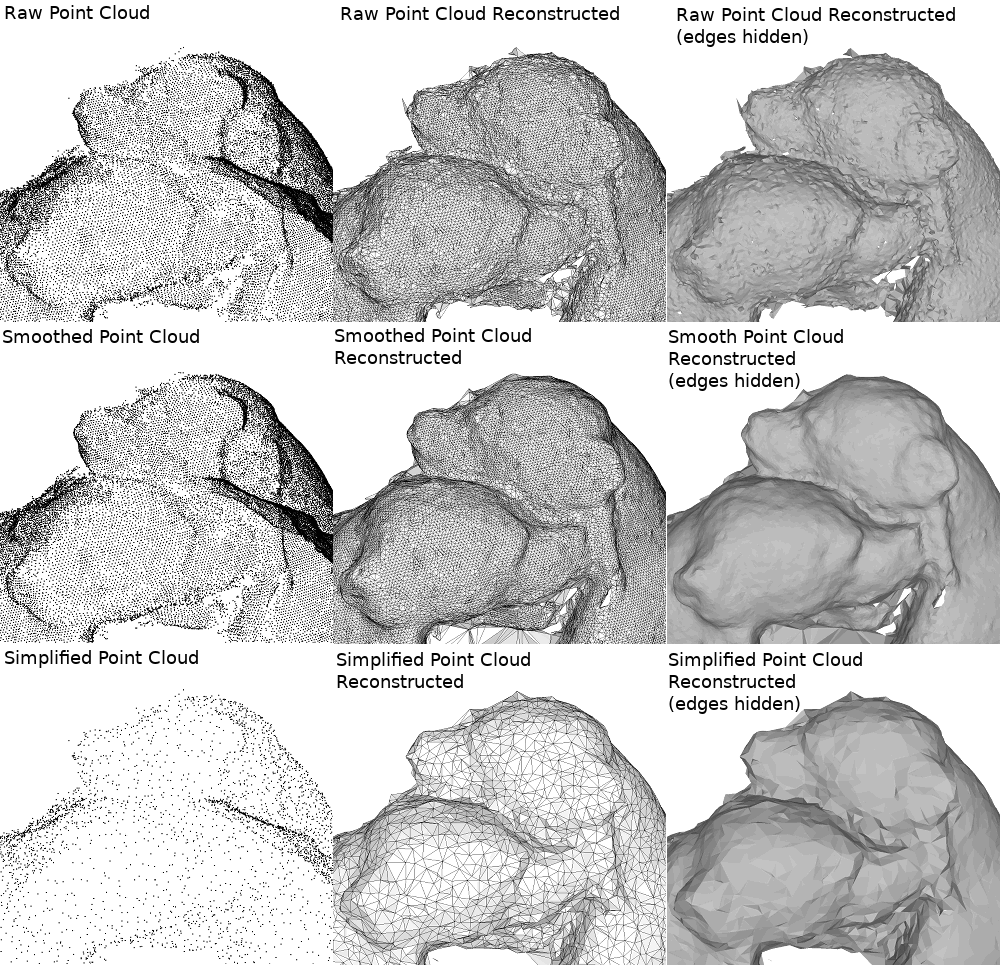
The following figure an example of a full reconstruction pipeline applied to a bear statue (courtesy EPFL Computer Graphics and Geometry Laboratory [5]). Two mesh processing algorithms (hole filling and isotropic remeshing) are also applied (refer to the chapter Polygon Mesh Processing for more information).
