#include <CGAL/Periodic_2_triangulation_2.h>

Inherits from

CGAL::Triangulation_cw_ccw_2.

Inherited by CGAL::Periodic_2_Delaunay_triangulation_2< Traits, Tds >.

Definition

The class Periodic_2_triangulation_2 represents a 2-dimensional triangulation of a point set in \( \mathbb T_c^2\).

Template Parameters

Traits	is the geometric traits, it is to be instantiated by a model of the concept `Periodic_2TriangulationTraits_2`.
TDS	is the triangulation data structure, it has to be instantiated by a model of the concept `TriangulationDataStructure_2` with some additional functionality in faces. By default, the triangulation data structure is instantiated by `CGAL::Triangulation_data_structure_2 < CGAL::Triangulation_vertex_base_2<Gt>, CGAL::Periodic_2_triangulation_face_base_2<Gt> > >`.

Traversal of the Triangulation

The periodic triangulation class provides several iterators and circulators that allow one to traverse it.

I/O

The I/O operators are defined for iostream. The format for the iostream is an internal format.

The information in the iostream is:

the original domain
the number of sheets of the covering space as in number_of_sheets()
the number of vertices
the non-combinatorial information of vertices (point resp. point-offset pairs, etc.)
the number of faces
the indices of the vertices of each face
the indices of the neighbors of each face, where the index corresponds to the preceding list of faces
the offsets corresponding to the vertices of the faces
the non-combinatorial information of each face

Implementation

Locate is implemented by a randomized walk from a vertex of the face given as optional parameter (or from an arbitrary vertex of if no optional parameter is given).

Insertion of a point is done by locating a face that contains the point, and then splitting this face. Apart from the location, insertion takes a time \( O(1)\).

Removal of a vertex is more difficult than in the Euclidean space, since the star of a vertex may not be disjoint from the star of a virtual copy of that vertex. Therefore generic removal of vertices is not implemented. Several more constrained cases are implemented: the removal of the last vertex in the triangulation and the removal of a vertex of degree 3.

The face, edge, and vertex iterators on features are derived from their counterparts visiting all (non-virtual and virtual) features which are themselves derived from the corresponding iterators of the triangulation data structure.

See also: Triangulation_2; Periodic_2TriangulationTraits_2; TriangulationDataStructure_2; TriangulationDataStructure_2::Face; TriangulationDataStructure_2::Vertex; CGAL::Triangulation_data_structure_2<Vb,Fb>; CGAL::Periodic_2_triangulation_face_base_2<Traits>

Public Types
enum	Iterator_type { STORED = 0, UNIQUE, STORED_COVER_DOMAIN, UNIQUE_COVER_DOMAIN }
	The enum Iterator_type is defined by `Periodic_2_triangulation_2` to specify the behavior of geometric iterators. More...

enum	Locate_type { VERTEX = 0, EDGE, FACE, EMPTY }
	The enum `@` is defined by `Periodic_2_triangulation_2` to specify which case occurs when locating a point in the triangulation. More...

Related Functions
(Note that these are not member functions.)
ostream &	operator<< (ostream &os, const Periodic_2_triangulation_2< Traits, Tds > &t)
	Writes the triangulation `t` into the stream `os`. More...

istream &	operator>> (istream &is, Triangulation_2< Traits, Tds > &t)
	Reads a triangulation from stream `is` and assigns it to `t`. More...

Types
typedef Traits	Geom_traits
	the traits class.

typedef Tds	Triangulation_data_structure
	the triangulation data structure type.

typedef Geom_traits::Periodic_2_offset_2	Offset
	the offset type.

typedef Geom_traits::Iso_rectangle_2	Iso_rectangle
	the iso rectangle type.

typedef array< int, 2 >	Covering_sheets
	integer tuple to store the number of sheets in each direction of space.

typedef Geom_traits::Point_2	Point
	the point type.

typedef Geom_traits::Segment_2	Segment
	the segment type.

typedef Geom_traits::Triangle_2	Triangle
	the triangle type.

typedef std::pair< Point, Offset >	Periodic_point
	represents a point-offset pair. More...

typedef array< Periodic_point, 2 >	Periodic_segment
	a pair of periodic points representing a segment in the periodic domain.

typedef array< Periodic_point, 3 >	Periodic_triangle
	a triple of periodic points representing a triangle in the periodic domain.

typedef Tds::Vertex	Vertex
	the vertex type.

typedef Tds::Face	Face
	the face type.

typedef Tds::Edge	Edge
	the edge type.

typedef Tds::size_type	size_type
	size type (an unsigned integral type).

typedef Tds::difference_type	difference_type
	difference type (a signed integral type).

Handles, Iterators and Circulators
The vertices and faces of the triangulations are accessed through `handles`, `iterators` and `circulators`. The handles are Is Model Of: of the concept `Handle` which basically offers the two dereference operators and `->`. The iterators and circulators are all bidirectional and non-mutable. The circulators and iterators are convertible to handles with the same value type, so that whenever a handle appear in the parameter list of a function, an appropriate iterator or circulator can be passed as well. The edges of the triangulation can also be visited through iterators and circulators, the edge circulators and iterators are also bidirectional and non-mutable.
typedef Tds::Vertex_handle	Vertex_handle
	handle to a vertex.

typedef Tds::Face_handle	Face_handle
	handle to a face.

typedef Tds::Face_iterator	Face_iterator
	iterator over all faces.

typedef Tds::Edge_iterator	Edge_iterator
	iterator over all edges.

typedef Tds::Vertex_iterator	Vertex_iterator
	iterator over all vertices.

typedef unspecified_type	Unique_vertex_iterator
	iterator over the vertices whose corresponding points lie in the original domain, i.e. More...

typedef Face_iterator	Finite_faces_iterator

typedef Edge_iterator	Finite_edges_iterator

typedef Vertex_iterator	Finite_vertices_iterator

typedef Face_iterator	All_faces_iterator

typedef unspecified_type	Face_circulator
	circulator over all faces incident to a given vertex.

typedef unspecified_type	Edge_circulator
	circulator over all edges incident to a given vertex.

typedef unspecified_type	Vertex_circulator
	circulator over all vertices adjacent to a given vertex.

Geometric iterators:
typedef unspecified_type	Periodic_triangle_iterator
	iterator over the triangles corresponding to faces of the triangulation.

typedef unspecified_type	Periodic_segment_iterator
	iterator over the segments corresponding to edges of the triangulation.

typedef unspecified_type	Periodic_point_iterator
	iterator over the points corresponding to vertices of the triangulation.

Creation
	Triangulation_2 (const Iso_rectangle &domain=Iso_rectangle(0, 0, 1, 1), const Geom_traits &traits=Geom_traits())
	Introduces an empty triangulation `t` with `domain` as original domain. More...

	Triangulation_2 (const Triangulation_2 &tr)
	Copy constructor. More...

Triangulation_2	operator= (const Triangulation_2< Traits, Tds > &tr)
	Assignment. More...

void	swap (Triangulation_2 &tr)
	The triangulations `tr` and `this` are swapped. More...

void	clear ()
	Deletes all faces and vertices resulting in an empty triangulation.

Access Functions
The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of the `tds`.
const Geom_traits &	geom_traits () const
	Returns a const reference to the triangulation traits object.

const Triangulation_data_structure_2 &	tds () const
	Returns a const reference to the triangulation data structure.

Iso_rectangle	domain () const
	Returns the original domain.

Covering_sheets	number_of_sheets () const
	Returns the number of sheets of the covering space the triangulation is currently computed in.

int	dimension () const
	Returns the dimension of the convex hull. More...

size_type	number_of_vertices () const
	Returns the number of vertices. More...

size_type	number_of_faces () const
	Returns the number of faces. More...

size_type	number_of_stored_vertices () const
	Returns the number of vertices in the data structure. More...

size_type	number_of_stored_faces () const
	Returns the number of faces in the data structure. More...

Non const access
Advanced This method is mainly a help for users implementing their own triangulation algorithms.
Triangulation_data_structure_2 &	tds ()
	This is an advanced function. More...

Non-constant-time access functions
size_type	number_of_edges () const
	Returns the number of edges. More...

size_type	number_of_stored_edges () const
	Returns the number of edges in the data structure. More...

Non-constant-time queries and conversions
Advanced It is not recommended to interfere with the built-in covering management. Especially a premature conversion to the 1-sheeted covering space might lead to problems when modifying the triangulation later.
bool	is_extensible_triangulation_in_1_sheet_h1 () const
	This is an advanced function. More...

bool	is_extensible_triangulation_in_1_sheet_h2 () const
	This is an advanced function. More...

bool	is_triangulation_in_1_sheet () const
	This is an advanced function. More...

void	convert_to_1_sheeted_covering ()
	This is an advanced function. More...

void	convert_to_9_sheeted_covering ()
	This is an advanced function. More...

Geometric access functions
Periodic_point	periodic_point (const Vertex_handle v) const
	Returns the periodic point given by vertex `v`. More...

Periodic_point	periodic_point (const Face_handle f, int i) const
	If `this` is represented in the 1-sheeted covering space, this function returns the periodic point given by the \( i\)-th vertex of face `f`, that is the point in the original domain and the offset of the vertex in `f`. More...

Periodic_segment	periodic_segment (const Face_handle f, int i) const
	Returns the periodic segment formed by the two point-offset pairs corresponding to the two vertices of edge `(f,i)`. More...

Periodic_segment	periodic_segment (const Edge &e) const
	Same as the previous method for edge `e`.

Periodic_triangle	periodic_triangle (const Face_handle f) const
	Returns the periodic triangle formed by the three point-offset pairs corresponding to the three vertices of facet `f`.

Note that a traits class providing exact constructions should be used in order to guarantee the following operations to be exact (as opposed to computing the triangulation only, which requires only exact predicates).
Point	point (const Periodic_point &pp) const
	Converts the `Periodic_point` `pp` (point-offset pair) to the corresponding `Point` in \( \mathbb R^3\).

Segment	segment (const Periodic_segment &s) const
	Converts the `Periodic_segment` `s` to a `Segment`.

Triangle	triangle (const Periodic_triangle &t) const
	Converts the `Periodic_triangle` `this` to a `Triangle`.

Segment	segment (Face_handle f, int i) const
	Equivalent to the call `t.segment(t.periodic_segment(f,i));`

Segment	segment (const Edge &e) const
	Equivalent to the call `t.segment(t.periodic_segment(e));`

Segment	segment (const Edge_circulator &ec) const
	Equivalent to the call `t.segment(t.periodic_segment(ec->first, ec->second));`

Segment	segment (const Edge_iterator &ei) const
	Equivalent to the call `t.segment(t.periodic_segment(ei->first, ei->second));`

Triangle	triangle (Face_handle f) const
	Equivalent to the call `t.triangle(t.periodic_triangle(f));`

Predicates
The class `Periodic_2_triangulation_2` provides methods to test the presence in the triangulation of a particular feature (edge or face).
bool	is_edge (Vertex_handle va, Vertex_handle vb)
	`true` if there is an edge having `va` and `vb` as vertices.

bool	is_edge (Vertex_handle va, Vertex_handle vb, Face_handle &fr, int &i)
	as above. More...

bool	is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3)
	`true` if there is a face having `v1`, `v2` and `v3` as vertices.

bool	is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3, Face_handle &fr)
	as above. More...

Queries
The class `Periodic_2_triangulation_2` provides methods to locate a given point with respect to a triangulation. It also provides methods to locate a point with respect to a given face of the triangulation.
Face_handle	locate (const Point &query, Face_handle f=Face_handle()) const
	If the triangulation is not empty, a face that contains the query in its interior or on its boundary is returned. More...

Face_handle	locate (const Point &query, Locate_type &lt, int &li, Face_handle h=Face_handle()) const
	Same as above. More...

Oriented_side	oriented_side (Face_handle f, const Point &p) const
	Returns on which side of the oriented boundary of `f` the point `p` lies.

Face, Edge and Vertex Iterators
The following iterators allow the user to visit faces, edges and vertices of the stored triangulation, i.e. in case of computing in a multiply sheeted covering space all stored periodic copies of each item are returned. These iterators are non-mutable, bidirectional and their value types are respectively `Face`, `Edge` and `Vertex`. They are all invalidated by any change in the triangulation.
Vertex_iterator	vertices_begin () const
	Starts at an arbitrary vertex.

Vertex_iterator	vertices_end () const
	Past-the-end iterator.

Edge_iterator	edges_begin () const
	Starts at an arbitrary edge.

Edge_iterator	edges_end () const
	Past-the-end iterator.

Face_iterator	faces_begin () const
	Starts at an arbitrary face.

Face_iterator	faces_end () const
	Past-the-end iterator.

Geometric iterators
The following iterators allow the user to obtain geometric primitives corresponding to faces, edges, and vertices of the triangulation. These iterators are non-mutable, bidirectional and their value types are respectively 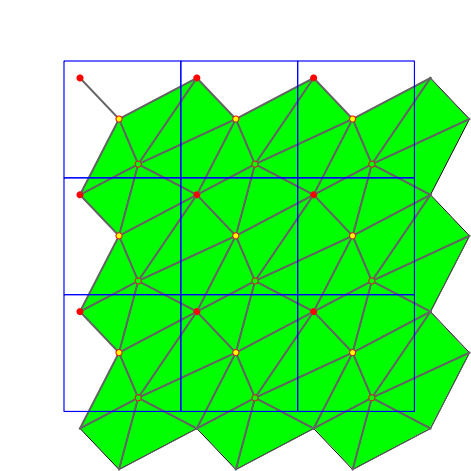`Periodic_triangle`, `Periodic_segment` and `Periodic_point`. They are all invalidated by any change in the triangulation. If the periodic triangulation is not computed in the 1-sheeted covering space, these iterators can be used to retain only the geometric primitives in the original domain. This can be controlled using the enum `Iterator_type`, see CGAL::Periodic_2_triangulation_2::Iterator_type. 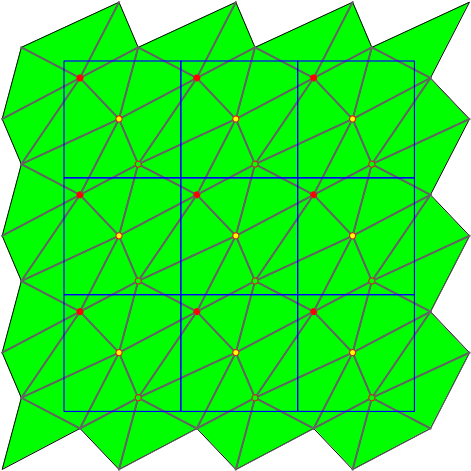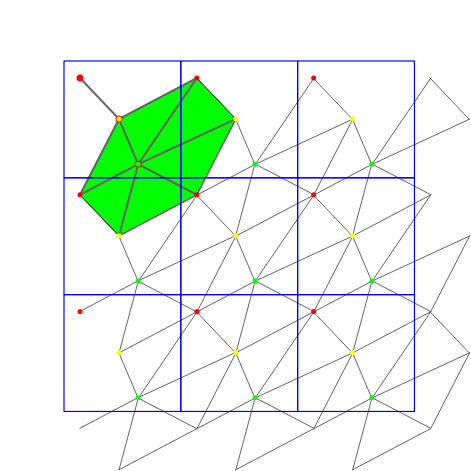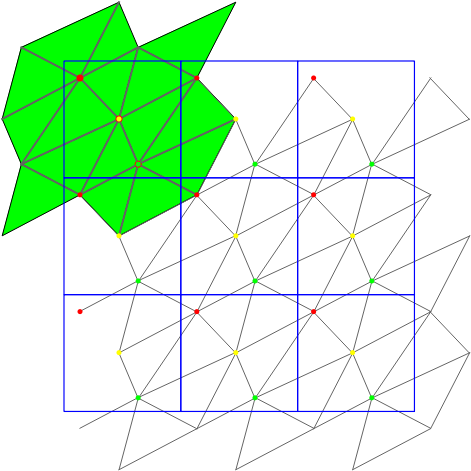The four different modes of the geometric iterators: `STORED`, `STORED_COVER_DOMAIN`, `UNIQUE`, `UNIQUE_COVER_DOMAIN`. Note that in case of computing in the 1-sheeted covering space, stored and unique give the same result.
Periodic_point_iterator	periodic_points_begin (Iterator_type it=STORED) const
	Iterates over the points of the triangulation. More...

Periodic_point_iterator	periodic_points_end (Iterator_type it=STORED) const
	Past-the-end iterator. More...

Periodic_segment_iterator	periodic_segments_begin (Iterator_type it=STORED) const
	Iterates over the segments of the triangulation. More...

Periodic_segment_iterator	periodic_segments_end (Iterator_type it=STORED) const
	Past-the-end iterator. More...

Periodic_triangle_iterator	periodic_triangles_begin (Iterator_type it=STORED) const
	Iterates over the triangles of the triangulation. More...

Periodic_triangle_iterator	periodic_triangles_end (Iterator_type it=STORED) const
	Past-the-end iterator. More...

Face, Edge and Vertex Circulators
The triangulation also provides circulators that allows to visit respectively all faces or edges incident to a given vertex or all vertices adjacent to a given vertex. These circulators are non-mutable and bidirectional. The `operator++` moves the circulator counterclockwise around the vertex while the `operator-` moves clockwise. A face circulator is invalidated by any modification of the face pointed to. An edge or a vertex circulator are invalidated by any modification of one of the two faces incident to the edge pointed to.
Face_circulator	incident_faces (Vertex_handle v) const
	Starts at an arbitrary face incident to `v`.

Face_circulator	incident_faces (Vertex_handle v, Face_handle f) const
	Starts at face `f`. More...

Edge_circulator	incident_edges (Vertex_handle v) const
	Starts at an arbitrary edge incident to `v`.

Edge_circulator	incident_edges (Vertex_handle v, Face_handle f) const
	Starts at the first edge of `f` incident to `v`, in counterclockwise order around `v`. More...

Vertex_circulator	adjacent_vertices (Vertex_handle v) const
	Starts at an arbitrary vertex adjacent to `v`.

Vertex_circulator	adjacent_vertices (Vertex_handle v, Face_handle f)
	Starts at the first vertex of `f` adjacent to `v` in counterclockwise order around `v`. More...

Traversal between adjacent faces
Vertex_handle	mirror_vertex (Face_handle f, int i) const
	returns the vertex of the \( i^{th}\) neighbor of `f` that is opposite to `f`. More...

int	mirror_index (Face_handle f, int i) const
	returns the index of `f` in its \( i^{th}\) neighbor. More...

Vertex_handle	insert (const Point &p, Face_handle f=Face_handle())

Vertex_handle	insert (const Point &p, Locate_type lt, Face_handle loc, int li)

Vertex_handle	push_back (const Point &p)

template<class InputIterator >
int	insert (InputIterator first, InputIterator last)

Advanced The following member functions offer more specialized versions of the insertion or removal operations to be used when one knows to be in the corresponding case. 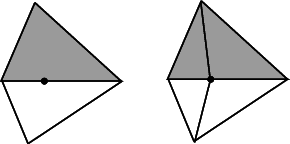Insertion of a point on an edge. 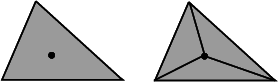Insertion in a face. The following functions are mainly intended to be used in conjunction with the `find_conflicts()` member functions of Delaunay and constrained Delaunay triangulations to perform insertions.
Vertex_handle	insert_first (const Point &p)
	This is an advanced function. More...

Vertex_handle	insert_in_face (const Point &p, Face_handle f)
	This is an advanced function. More...

void	remove_degree_3 (Vertex_handle v)
	This is an advanced function. More...

void	remove_first (Vertex_handle v)
	This is an advanced function. More...

template<class EdgeIt >
Vertex_handle	star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end)
	This is an advanced function. More...

template<class EdgeIt , class FaceIt >
Vertex_handle	star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end, FaceIt face_begin, FaceIt face_end)
	This is an advanced function. More...

void	set_domain (const Iso_rectangle dom)
	This is an advanced function. More...

Miscellaneous
int	ccw (int i) const
	Returns \( i+1\) modulo 3. More...

int	cw (int i) const
	Returns \( i+2\) modulo 3. More...

void	flippable (Face_handle f, int i)

size_t	degree (Vertex_handle v)
	Returns the degree of the vertex `v`

Checking
Advanced The responsibility of keeping a valid triangulation belongs to the users if advanced operations are used. Obviously the advanced user, who implements higher levels operations may have to make a triangulation invalid at some times. The following method is provided to help the debugging.
bool	is_valid (bool verbose=false, int level=0) const
	This is an advanced function. More...

Additional Inherited Members
Public Member Functions inherited from CGAL::Triangulation_cw_ccw_2
	Triangulation_cw_ccw_2 ()

int	ccw (const int i) const

int	cw (const int i) const

Member Typedef Documentation

◆ Periodic_point

template<typename Traits , typename Tds >

typedef std::pair< Point, Offset > CGAL::Periodic_2_triangulation_2< Traits, Tds >::Periodic_point

represents a point-offset pair.

The point in the pair lies in the original domain.

◆ Unique_vertex_iterator

template<typename Traits , typename Tds >

typedef unspecified_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::Unique_vertex_iterator

iterator over the vertices whose corresponding points lie in the original domain, i.e.

for each set of periodic copies the Unique_vertex_iterator iterates over exactly one representative.

Member Enumeration Documentation

◆ Iterator_type

template<typename Traits , typename Tds >

enum CGAL::Periodic_2_triangulation_2::Iterator_type

The enum Iterator_type is defined by Periodic_2_triangulation_2 to specify the behavior of geometric iterators.

Enumerator
STORED	Return all geometric primitives as they are stored internally in `Triangulation_data_structure_2`.
UNIQUE	Return only one representative of each geometric primitive even if the triangulation is computed in a multiply sheeted covering space. Choose the representative whose maximum offset is minimal but non-negative in each direction of space.
STORED_COVER_DOMAIN	Same as `STORED` but return additionally all primitives whose intersection with the original domain of the current covering space is non-empty.
UNIQUE_COVER_DOMAIN	Same as `UNIQUE` but return additionally all primitives whose intersection with the original domain is non-empty.

◆ Locate_type

template<typename Traits , typename Tds >

enum CGAL::Periodic_2_triangulation_2::Locate_type

The enum @ is defined by Periodic_2_triangulation_2 to specify which case occurs when locating a point in the triangulation.

If the triangulation does not contain any points EMPTY is returned.

Enumerator
VERTEX	when the located point coincides with a vertex of the triangulation
EDGE	when the point is in the relative interior of an edge
FACE	when the point is in the interior of a facet
EMPTY	when the triangulation is empty

Member Function Documentation

◆ adjacent_vertices()

template<typename Traits , typename Tds >

Vertex_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::adjacent_vertices	(	Vertex_handle	v,
		Face_handle	f
	)

Starts at the first vertex of f adjacent to v in counterclockwise order around v.

Precondition: Face f is incident to vertex v.

◆ ccw()

template<typename Traits , typename Tds >

int CGAL::Periodic_2_triangulation_2< Traits, Tds >::ccw ( int i ) const

Returns \( i+1\) modulo 3.

Precondition: \(0 \leq i \leq 2\).

◆ convert_to_1_sheeted_covering()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::convert_to_1_sheeted_covering ( )

This is an advanced function.

Advanced

Converts the current triangulation into the same periodic triangulation in the 1-sheeted covering space.

Precondition: is_triangulation_in_1_sheet()

◆ convert_to_9_sheeted_covering()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::convert_to_9_sheeted_covering ( )

This is an advanced function.

Advanced

Converts the current triangulation into the same periodic triangulation in the 9-sheeted covering space.

◆ cw()

template<typename Traits , typename Tds >

int CGAL::Periodic_2_triangulation_2< Traits, Tds >::cw ( int i ) const

Returns \( i+2\) modulo 3.

Precondition: \(0 \leq i \leq 2\).

◆ dimension()

template<typename Traits , typename Tds >

int CGAL::Periodic_2_triangulation_2< Traits, Tds >::dimension ( ) const

Returns the dimension of the convex hull.

The dimension is zero if the triangulation is empty and two otherwise.

◆ incident_edges()

template<typename Traits , typename Tds >

Edge_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::incident_edges	(	Vertex_handle	v,
		Face_handle	f
	)		const

Starts at the first edge of f incident to v, in counterclockwise order around v.

Precondition: Face f is incident to vertex v.

◆ incident_faces()

template<typename Traits , typename Tds >

Face_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::incident_faces	(	Vertex_handle	v,
		Face_handle	f
	)		const

Starts at face f.

Precondition: Face f is incident to vertex v.

◆ insert_first()

template<typename Traits , typename Tds >

Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::insert_first ( const Point & p )

This is an advanced function.

Advanced

Inserts the first vertex.

◆ insert_in_face()

template<typename Traits , typename Tds >

Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::insert_in_face	(	const Point &	p,
		Face_handle	f
	)

This is an advanced function.

Advanced

Inserts vertex v in face f. Face f is modified, two new faces are created. If the triangulation contains periodic copies, a point is inserted in all periodic copies.

Precondition: The point in vertex v lies inside face f.

◆ is_edge()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_edge	(	Vertex_handle	va,
		Vertex_handle	vb,
		Face_handle &	fr,
		int &	i
	)

as above.

In addition, if true is returned, the edge with vertices va and vb is the edge e=(fr,i) where fr is a handle to the face incident to e and on the right side of e oriented from va to vb.

◆ is_extensible_triangulation_in_1_sheet_h1()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_extensible_triangulation_in_1_sheet_h1 ( ) const

This is an advanced function.

Advanced

The current triangulation remains a triangulation in the 1-sheeted covering space even after adding points if this method returns true. This test relies on a heuristic, i.e. if it answers false nothing is known. This test runs in constant-time when not computing in the 1-sheeted covering space. (This test uses the length of the longest edge in the triangulation as a criterion [1].)

◆ is_extensible_triangulation_in_1_sheet_h2()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_extensible_triangulation_in_1_sheet_h2 ( ) const

This is an advanced function.

Advanced

The same as is_extensible_triangulation_in_1_sheet_h1() but with a more precise heuristic, i.e. it might answer true in cases in which is_extensible_triangulation_in_1_sheet_h1() would not. However, it is much less time efficient when not computing in the 1-sheeted covering space. (This test uses the diameter of the largest empty circle in the input point set as a criterion [1].)

◆ is_face()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_face	(	Vertex_handle	v1,
		Vertex_handle	v2,
		Vertex_handle	v3,
		Face_handle &	fr
	)

as above.

In addition, if true is returned, fr is a handle to the face with v1, v2 and v3 as vertices.

◆ is_triangulation_in_1_sheet()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_triangulation_in_1_sheet ( ) const

This is an advanced function.

Advanced

Returns true if the current triangulation would still be a triangulation in the 1-sheeted covering space, returns false otherwise.

◆ is_valid()

template<typename Traits , typename Tds >

bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_valid	(	bool	verbose = `false`,
		int	level = `0`
	)		const

This is an advanced function.

Advanced

Checks the combinatorial validity of the triangulation and also the validity of its geometric embedding. This method is mainly a debugging help for the users of advanced features.

◆ locate() [1/2]

template<typename Traits , typename Tds >

Face_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::locate	(	const Point &	query,
		Face_handle	f = `Face_handle()`
	)		const

If the triangulation is not empty, a face that contains the query in its interior or on its boundary is returned.

If the triangulation is empty, the default constructed Face_handle is returned.

◆ locate() [2/2]

template<typename Traits , typename Tds >

Face_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::locate	(	const Point &	query,
		Locate_type &	lt,
		int &	li,
		Face_handle	h = `Face_handle()`
	)		const

Same as above.

Additionally, the parameters lt and li describe where the query point is located. The variable lt is set to the locate type of the query. If lt==VERTEX the variable li is set to the index of the vertex, and if lt==EDGE li is set to the index of the vertex opposite to the edge. Be careful that li has no meaning when the query type is FACE or when the triangulation is \( 0\)-dimensional.

◆ mirror_index()

template<typename Traits , typename Tds >

int CGAL::Periodic_2_triangulation_2< Traits, Tds >::mirror_index	(	Face_handle	f,
		int	i
	)		const

returns the index of f in its \( i^{th}\) neighbor.

Precondition: \(0 \leq i \leq 2\).

◆ mirror_vertex()

template<typename Traits , typename Tds >

Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::mirror_vertex	(	Face_handle	f,
		int	i
	)		const

returns the vertex of the \( i^{th}\) neighbor of f that is opposite to f.

Precondition: \( 0 \leq i \leq 2\).

◆ number_of_edges()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_edges ( ) const

Returns the number of edges.

Counts all edges that are representatives of the same segment in \( \mathbb T_c^2\) as one edge.

◆ number_of_faces()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_faces ( ) const

Returns the number of faces.

Counts all faces that are representatives of the same triangle in \( \mathbb T_c^2\) as one face.

◆ number_of_stored_edges()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_edges ( ) const

Returns the number of edges in the data structure.

This is the same as the number of sheets times number_of_edges().

◆ number_of_stored_faces()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_faces ( ) const

Returns the number of faces in the data structure.

This is the same as the number of sheets times number_of_faces().

◆ number_of_stored_vertices()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_vertices ( ) const

Returns the number of vertices in the data structure.

This is the same as the number of sheets times number_of_vertices().

◆ number_of_vertices()

template<typename Traits , typename Tds >

size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_vertices ( ) const

Returns the number of vertices.

Counts all vertices that are representatives of the same point in \( \mathbb T_c^2\) as one vertex.

◆ operator=()

template<typename Traits , typename Tds >

Triangulation_2 CGAL::Periodic_2_triangulation_2< Traits, Tds >::operator= ( const Triangulation_2< Traits, Tds > & tr )

Assignment.

All the vertices and faces are duplicated. After the assignment, this and tr refer to different triangulations: if tr is modified, this is not.

◆ periodic_point() [1/2]

template<typename Traits , typename Tds >

Periodic_point CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_point ( const Vertex_handle v ) const

Returns the periodic point given by vertex v.

If this is represented in the 1-sheeted covering space, the offset is always zero. Otherwise v can correspond to a periodic copy outside the domain of an input point.

◆ periodic_point() [2/2]

template<typename Traits , typename Tds >

Periodic_point CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_point	(	const Face_handle	f,
		int	i
	)		const

If this is represented in the 1-sheeted covering space, this function returns the periodic point given by the \( i\)-th vertex of face f, that is the point in the original domain and the offset of the vertex in f.

If this is represented in the 9-sheeted covering space, this offset is possibly added to another offset determining the periodic copy.

Precondition: \( i \in\{0,1,2\}\)

◆ periodic_points_begin()

template<typename Traits , typename Tds >

Periodic_point_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_points_begin ( Iterator_type it = STORED ) const

Iterates over the points of the triangulation.

Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.

◆ periodic_points_end()

template<typename Traits , typename Tds >

Periodic_point_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_points_end ( Iterator_type it = STORED ) const

Past-the-end iterator.

Note that to match another Periodic_point_iterator both must have the same Iterator_type it.

◆ periodic_segment()

template<typename Traits , typename Tds >

Periodic_segment CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segment	(	const Face_handle	f,
		int	i
	)		const

Returns the periodic segment formed by the two point-offset pairs corresponding to the two vertices of edge (f,i).

Precondition: \( i \in\{0,1,2\}\)

◆ periodic_segments_begin()

template<typename Traits , typename Tds >

Periodic_segment_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segments_begin ( Iterator_type it = STORED ) const

Iterates over the segments of the triangulation.

Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.

◆ periodic_segments_end()

template<typename Traits , typename Tds >

Periodic_segment_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segments_end ( Iterator_type it = STORED ) const

Past-the-end iterator.

Note that to match another Periodic_segment_iterator both must have the same Iterator_type it.

◆ periodic_triangles_begin()

template<typename Traits , typename Tds >

Periodic_triangle_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_triangles_begin ( Iterator_type it = STORED ) const

Iterates over the triangles of the triangulation.

Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.

◆ periodic_triangles_end()

template<typename Traits , typename Tds >

Periodic_triangle_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_triangles_end ( Iterator_type it = STORED ) const

Past-the-end iterator.

Note that to match another Periodic_triangle_iterator both must have the same Iterator_type it.

◆ remove_degree_3()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::remove_degree_3 ( Vertex_handle v )

This is an advanced function.

Advanced

Removes a vertex of degree three. Two of the incident faces are destroyed, the third one is modified.

Precondition: Vertex v is a vertex with degree three.

◆ remove_first()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::remove_first ( Vertex_handle v )

This is an advanced function.

Advanced

Removes the unique vertex in the triangulation.

◆ set_domain()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::set_domain ( const Iso_rectangle dom )

This is an advanced function.

Advanced

Changes the domain. Note that this function calls clear(), i.e., it erases the existing triangulation.

◆ star_hole() [1/2]

template<typename Traits , typename Tds >

template<class EdgeIt >

Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::star_hole	(	Point	p,
		EdgeIt	edge_begin,
		EdgeIt	edge_end
	)

This is an advanced function.

Advanced

creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end]. Returns a handle to the new vertex.

Precondition: The triangulation is a triangulation of 1 sheet

◆ star_hole() [2/2]

template<typename Traits , typename Tds >

template<class EdgeIt , class FaceIt >

Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::star_hole	(	Point	p,
		EdgeIt	edge_begin,
		EdgeIt	edge_end,
		FaceIt	face_begin,
		FaceIt	face_end
	)

This is an advanced function.

Advanced

same as above, except that the algorithm first recycles faces in the sequence [face_begin, face_end] and create new ones only when the sequence is exhausted.

Precondition: The triangulation is a triangulation of 1 sheet

◆ swap()

template<typename Traits , typename Tds >

void CGAL::Periodic_2_triangulation_2< Traits, Tds >::swap ( Triangulation_2 & tr )

The triangulations tr and this are swapped.

t.swap(tr) should be preferred to this = tr or to t(tr) if tr is deleted after that.

◆ tds()

template<typename Traits , typename Tds >

Triangulation_data_structure_2& CGAL::Periodic_2_triangulation_2< Traits, Tds >::tds ( )

This is an advanced function.

Advanced

Returns a reference to the triangulation data structure.

◆ Triangulation_2() [1/2]

template<typename Traits , typename Tds >

CGAL::Periodic_2_triangulation_2< Traits, Tds >::Triangulation_2	(	const Iso_rectangle &	domain = `Iso_rectangle(0, 0, 1, 1)`,
		const Geom_traits &	traits = `Geom_traits()`
	)

Introduces an empty triangulation t with domain as original domain.

Precondition: domain is a square.

◆ Triangulation_2() [2/2]

template<typename Traits , typename Tds >

CGAL::Periodic_2_triangulation_2< Traits, Tds >::Triangulation_2 ( const Triangulation_2 & tr )

Copy constructor.

All the vertices and faces are duplicated. After the copy, this and tr refer to different triangulations: if tr is modified, this is not.

Friends And Related Function Documentation

◆ operator

template<typename Traits , typename Tds >

ostream & operator<< ( ostream & os,

const Periodic_2_triangulation_2< Traits, Tds > & t

)

related

Writes the triangulation `t` into the stream `os`.

Precondition
The output operator must be defined for `Point`.

◆ operator>>()

template<typename Traits , typename Tds >

istream & operator>>	(	istream &	is,
		Triangulation_2< Traits, Tds > &	t
	)

Precondition: The input operator must be defined for Point.

Inherits from

Definition

Public Types

Related Functions

Types

Handles, Iterators and Circulators

Geometric iterators:

Creation

Access Functions

Non const access

Non-constant-time access functions

Non-constant-time queries and conversions

Geometric access functions

Predicates

Queries

Face, Edge and Vertex Iterators

Geometric iterators

Face, Edge and Vertex Circulators

Traversal between adjacent faces

Miscellaneous

Checking

Additional Inherited Members

Member Typedef Documentation

◆ Periodic_point

◆ Unique_vertex_iterator

Member Enumeration Documentation

◆ Iterator_type

◆ Locate_type

Member Function Documentation

◆ adjacent_vertices()

◆ ccw()

◆ convert_to_1_sheeted_covering()

◆ convert_to_9_sheeted_covering()

◆ cw()

◆ dimension()

◆ incident_edges()

◆ incident_faces()

◆ insert_first()

◆ insert_in_face()

◆ is_edge()

◆ is_extensible_triangulation_in_1_sheet_h1()

◆ is_extensible_triangulation_in_1_sheet_h2()

◆ is_face()

◆ is_triangulation_in_1_sheet()

◆ is_valid()

◆ locate() [1/2]

◆ locate() [2/2]

◆ mirror_index()

◆ mirror_vertex()

◆ number_of_edges()

◆ number_of_faces()

◆ number_of_stored_edges()

◆ number_of_stored_faces()

◆ number_of_stored_vertices()

◆ number_of_vertices()

◆ operator=()

◆ periodic_point() [1/2]

◆ periodic_point() [2/2]

◆ periodic_points_begin()

◆ periodic_points_end()

◆ periodic_segment()

◆ periodic_segments_begin()

◆ periodic_segments_end()

◆ periodic_triangles_begin()

◆ periodic_triangles_end()

◆ remove_degree_3()

◆ remove_first()

◆ set_domain()

◆ star_hole() [1/2]

◆ star_hole() [2/2]

◆ swap()

◆ tds()

◆ Triangulation_2() [1/2]

◆ Triangulation_2() [2/2]

Friends And Related Function Documentation

◆ operator template<typename Traits , typename Tds > ostream & operator<< ( ostream & os, const Periodic_2_triangulation_2< Traits, Tds > & t ) related Writes the triangulation t into the stream os. PreconditionThe output operator must be defined for Point.

◆ operator>>()

◆ operator

template<typename Traits , typename Tds >

ostream & operator<< ( ostream & os,

const Periodic_2_triangulation_2< Traits, Tds > & t

)

related

Writes the triangulation `t` into the stream `os`.

Precondition
The output operator must be defined for `Point`.