Chapter 51
Geometric Optimisation

Geometric optimisation deals with problems of computing geometric objects which are optimal subject to certain criteria and constraints. Our running example will be the problem of computing the sphere of smallest radius which contains a given point set in $$d-dimensional Euclidean space.

The geometric optimisation algorithms in CGAL fall into three categories, ``Bounding Volumes'', ``Optimal Distances'' and ``Advanced Techniques''.

51.1   Bounding and Inscribed Volumes

This category contains algorithms which for a given point set compute the ``best'' circumscribing (or inscribed) object from a specific class. If the class consists of all spheres in $$d-dimensional Euclidean space and ``best'' is defined as having smallest radius, then we obtain the smallest enclosing sphere problem already mentioned above.

In the following example a smallest enclosing circle (CGAL::Min_circle_2<Traits>) is constructed from points on a line and written to standard output. The example shows that it is advisable to switch on random shuffling in order to deal with a `bad' order of the input points.

#include <CGAL/Homogeneous.h>
#include <CGAL/Min_circle_2.h>
#include <CGAL/Min_circle_2_traits_2.h>
#include <CGAL/Gmpz.h>
#include <iostream>

// typedefs
typedef  CGAL::Gmpz                      NT;
typedef  CGAL::Homogeneous<NT>           K;
typedef  CGAL::Min_circle_2_traits_2<K>  Traits;
typedef  CGAL::Min_circle_2<Traits>      Min_circle;

typedef  K::Point_2                      Point;

// main
int
main( int, char**)
{
    int     n = 100;
    Point*  P = new Point[ n];

    for ( int i = 0; i < n; ++i)
	P[ i] = Point( (i%2 == 0 ? i : -i), 0);
    // (0,0), (-1,0), (2,0), (-3,0), ...

    Min_circle  mc1( P, P+n, false);    // very slow
    Min_circle  mc2( P, P+n, true);     // fast

    CGAL::set_pretty_mode( std::cout);
    std::cout << mc2;

    delete[] P;

    return( 0);
}

Other classes for which we provide solutions are ellipses (CGAL::Min_ellipse_2<Traits>), rectangles (CGAL::min_rectangle_2), parallelograms (CGAL::min_parallelogram_2) and strips (CGAL::min_strip_2) in the plane, with appropriate optimality criteria. In addition to spheres for points (CGAL::Min_sphere_d<Traits>) and spheres for spheres (CGAL::Min_sphere_of_spheres_d<Traits>), there is another class of objects which allows for solutions in arbitrary dimension, namely annuli (CGAL::Min_annulus_d<Traits>).

Bounding volumes can be used to obtain simple approximations of complicated objects. For example, consider the problem of deciding whether two moving polygons currently intersect. An obvious solution is to discretize time and perform a full intersection test for any time step. If the polygons are far apart most of the time, this is unnecessary. Instead, simple bounding volumes (for examples, circles) are computed for both polygons at their initial positions. At subsequent time steps, an intersection test between the moving bounding circles replaces the actual intersection test; only if the circles do intersect, the expensive intersection test between the polygons is performed. In practice, bounding volume hierarchies are often used on top of simple bounding volumes to approximate complicated objects more accurately.

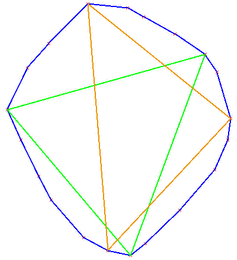
As far as inscribed volumes are concerned, we provide algorithms for computing maximal inscribed $$k-gons (triangles, quadrilaterals, ...) of a planar point set $$P. Maximal $$k-gons are convex, and it is known that their vertices can be chosen to be vertices of the convex hull of $$P. Hence, the functions CGAL::maximum_area_inscribed_k_gon_2 and CGAL::maximum_perimeter_inscribed_k_gon_2 operate on convex polygons only. The example below shows that the largest area triangle (green) and the largest perimeter triangle (orange, containing the top point) of a point set are different in general.

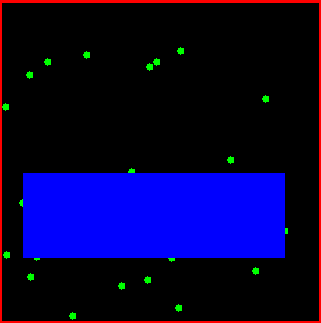
We further provide an algorithm for computing the maximal area inscribed axis parallel rectangle

Given a set of points in the plane, the class CGAL::Largest_empty_iso_rectangle_2<T> is a data structure that maintains an iso-rectangle with the largest area among all iso-rectangles that are inside a given iso-rectangles, and that do not contain any point of the point set.

Bounding and inscribed volumes are also frequently applied to extract geometric properties of objects. For example, the smallest enclosing annulus of a point set can be used to test whether a set of points is approximately cospherical. Here, the width of the annulus (or its area, or still another criterion that we use) is a good measure for this property. The largest area triangle is for example used in heuristics for matching archaeological aerial photographs. Largest perimeter triangles are used in scoring cross country soaring flights, where the goal is basically to fly as far as possible, but still return to the departure airfield. To score simply based on the total distance flown is not a good measure, since circling in thermals allows to increase it easily.

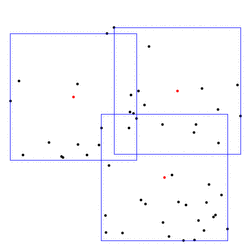
Bounding volumes also define geometric ``center points'' of objects. For example, if two objects are to be matched (approximately), one approch is to first apply the translation that maps the centers of their smallest enclosing spheres onto each other. Simpler centers are possible, of course (center of gravity, center of bounding box), but more advanced bounding volumes might give better results in some cases. It can also make sense to consider several center points instead of just one. For example, we provide algorithms to cover a planar point set with between two and four minimal boxes (CGAL::rectangular_p_center_2). Below is an example covering with three boxes; the center points are shown in red.

To avoid later disappointment: one very nice class of bounding volumes, namely ellipsoids in three- and higherdimensional space, is currently not supported by CGAL. The reason is that the algebraic complexity of this problem is still beyond the level which would allow us to come up with a solution that satisfies the CGAL standards. We are working on a solution for 3-space, though.

51.2   Optimal Distances

This section currently consists of two algorithms only. On one hand, one can compute the computation of the distance between the convex hulls of two given point sets in $$d-dimensional Euclidean space (CGAL::Polytope_distance_d<Traits>). Moreover, it is possible to compute the width of a point set in three dimensions (CGAL::Width_3<Traits>).

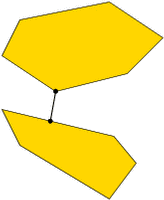
The obvious application is collision detection between convex bodies in space. In the spirit of the bounding volume application above, it also makes sense for nonconvex objects: a full intersection test between complicated objects could in a first stage be approximated with the test between the convex hulls of the objects. Only if the hulls intersect, a full intersection test is necessary.

To dampen fears concerning the performance of the distance computation, we want to mention that the convex hulls of the input point sets are not explicitly computed. This avoids a runtime which grows exponentially in $$d. In fact, the runtime is almost always linear in the size of the two point sets.

51.3   Advanced techniques

Geometric optimisation is a well-studied subject also in theory. Consequently, general design principles have been developed from which solutions to diverse problems arise. For example, although the problems of computing the smallest enclosing sphere of a point set and the problem of computing the distance between two convex hulls seem to be quite different, they are both instances of a more general optimisation problem, named ``quadratic programming''. To be more specific, CGAL's solutions for the two quadratic programming instances just mentioned are based on a general quadratic programming solver, which will be documented as a separate unit in future releases.

Two techniques that we make available in this section are CGAL::monotone_matrix_search and CGAL::sorted_matrix_search. They deal with the problem of efficiently finding largest entries in matrices with certain structural properties. Many concrete problems can be modelled as matrix search problems, and for some of them we provide explicit solutions that allow you to solve them without knowing about the matrix search technique. Examples are, the computation of all furthest neighbors for the vertices of a convex polygon, maximal $$k-gons inscribed into a planar point set, and computing rectangular $$p-centers.