
The basic 3D-triangulation class of CGAL is primarily designed to represent the triangulations of a set of points in . It is a partition of the convex hull of into tetrahedra whose vertices are the points of . Together with the unbounded cell having the convex hull boundary as its frontier, the triangulation forms a partition of . Its cells (-faces) are such that two cells either do not intersect or share a common facet (-face), edge (-face) or vertex (-face).
In order to deal only with tetrahedra, which is convenient for many applications, the unbounded cell can be subdivided into tetrahedra by considering that each convex hull facet is incident to an infinite cell having as fourth vertex an auxiliary vertex called the infinite vertex. In that way, each facet is incident to exactly two cells and special cases at the boundary of the convex hull are simple to deal with.
The class Triangulation_3<TriangulationTraits_3,TriangulationDataStructure_3> of CGAL implements this point of view and therefore considers the triangulation of the set of points as a set of finite and infinite tetrahedra. Notice that the infinite vertex has no significant coordinates and that no geometric predicate can be applied on it.
A triangulation is a collection of vertices and cells that are linked together through incidence and adjacency relations. Each cell gives access to its four incident vertices and to its four adjacent cells. Each vertex gives access to one of its incident cells.
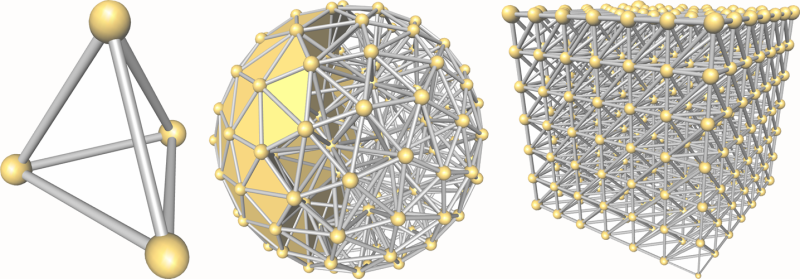
The four vertices of a cell are indexed with 0, 1, 2 and 3 in positive orientation, the positive orientation being defined by the orientation of the underlying Euclidean space (see Figure 22.1). The neighbors of a cell are also indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by is opposite to the vertex with the same index.
As in the underlying combinatorial triangulation (see Chapter 23), edges (-faces) and facets (-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex with index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of c with indices i and j). See Figure 23.1.
Degenerate Dimensions The class Triangulation_3 can also deal with triangulations whose dimension is less than 3. A triangulation of a set of points in covers the whole space and consists of cells having vertices: some of them are infinite, they are obtained by linking the additional infinite vertex to each facet of the convex hull of the points.
The same cell class is used in all cases: triangular faces in 2D can be considered as degenerate cells, having only three vertices (resp. neighbors) numbered ; edges in 1D have only two vertices (resp. neighbors) numbered and .
The implicit representation of facets (resp. edges) still holds for degenerate dimensions (i.e. dimensions ): in dimension 2, each cell has only one facet of index 3, and 3 edges , and ; in dimension 1, each cell has one edge .
Validity A triangulation of is said to be locally valid iff
(a)-(b) Its underlying combinatorial graph, the triangulation
data structure, is locally valid
(see Section 23.1 of Chapter 23)
(c) Any cell has its vertices ordered according to positive
orientation. See Figure 22.1.
When the triangulation is degenerated into a triangulation of dimension 2, the geometric validity reduces to:
(c-2D) For any two adjacent triangles and with common edge , and lie on opposite sides of in the plane.
When all the points are collinear, this condition becomes:
(c-1D) For any two adjacent edges and , and lie on opposite sides of the common vertex on the line.
The is_valid() method provided in Triangulation_3 checks the local validity of a given triangulation. This does not always ensure global validity [MNS96, DLPT98] but it is sufficient for practical cases.
The class Delaunay_triangulation_3 represents a three-dimensional Delaunay triangulation.
Delaunay triangulations have the specific empty sphere property, that is, the circumscribing sphere of each cell of such a triangulation does not contain any other vertex of the triangulation in its interior. These triangulations are uniquely defined except in degenerate cases where five points are cospherical. Note however that the CGAL implementation computes a unique triangulation even in these cases.
This implementation is fully dynamic: it supports both insertions of points and vertex removal. The user is advised to use the class Triangulation_hierarchy_3 in order to benefit from an increased efficiency for large data sets.
The class Regular_triangulation_3 implements incremental regular triangulations, also known as weighted Delaunay triangulations.
Let be a set of weighted points in . Let and be two weighted points. A weighted point can also be seen as a sphere of center and radius . The power product between and is defined as
where is the Euclidean distance between and . and are said to be orthogonal iff (see Figure 22.3).
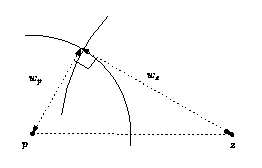
Four weighted points have a unique common orthogonal weighted point called the power sphere. The weighted point orthogonal to three weighted points in the plane defined by these three points is called the power circle. The power segment will denote the weighted point orthogonal to two weighted points on the line defined by these two points.
A sphere is said to be regular if .
A triangulation of is regular if the power spheres of all simplices are regular.
The regular triangulation of is in fact the projection onto of the convex hull of the four-dimensional points for . Note that all points of do not necessarily appear as vertices of the regular triangulation. To know more about regular triangulations, see for example [ES96].
When all weights are 0, power spheres are nothing more than circumscribing spheres, and the regular triangulation is exactly the Delaunay triangulation.
The class Triangulation_hierarchy_3 implements a triangulation augmented with a data structure that allows fast point location queries. Thus, it allows fast construction of the triangulation. As proved in [Dev02], this structure has an optimal behavior when it is built for Delaunay triangulations.
Note that, since the algorithms that are provided are randomized, the running time of constructing a triangulation with a hierarchy may be improved when shuffling the data points.
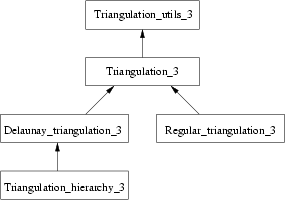
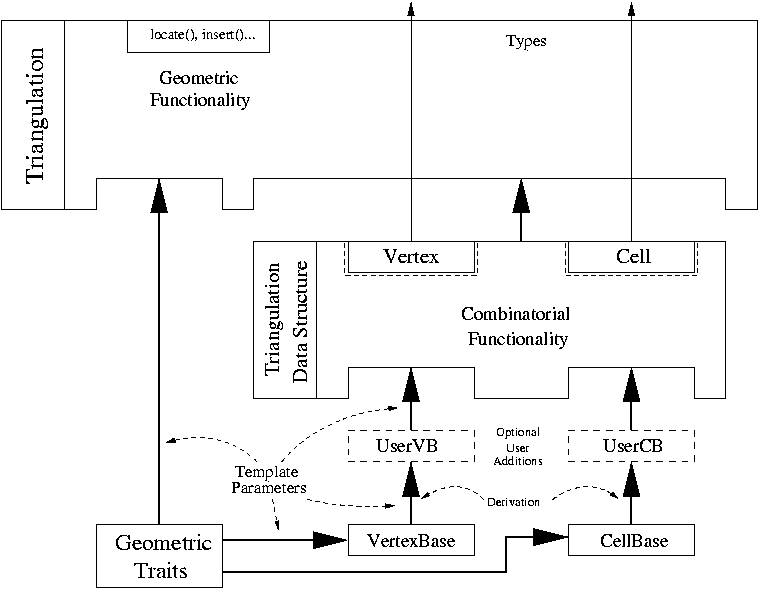
The main classes Triangulation_3, Delaunay_triangulation_3 and Regular_triangulation_3 are connected to each other by the derivation diagram shown in Figure 22.5. This diagram also shows two other classes: Triangulation_utils_3, which provides a set of tools operating on the indices of vertices in cells, and Triangulation_hierarchy_3, which implements a hierarchy of triangulations suitable for speeding up point location.
The three main classes (Triangulation_3, Delaunay_triangulation_3 and Regular_triangulation_3) provide high-level geometric functionality such as location of a point in the triangulation [DPT02], insertion and possibly removal of a point [DT03], and are responsible for the geometric validity. They are built as layers on top of a triangulation data structure, which stores their combinatorial structure. This separation between the geometry and the combinatorics is reflected in the software design by the fact that these three triangulation classes take two template parameters :
The class Triangulation_hierarchy_3 is parameterized by a class, which at the moment can only be Delaunay_triangulation_3. It fetches its geometric traits from this parameter directly.
The first template parameter of the triangulation class Triangulation_3<TriangulationTraits_3, TriangulationDataStructure_3> is the geometric traits class, described by the concept TriangulationTraits_3. It must define the types of the geometric objects (points, segments, triangles and tetrahedra) forming the triangulation together with a few geometric predicates on these objects: orientation in space, orientation in case of coplanar points, order of collinear points.
In addition to the requirements described before, the geometric traits class of Delaunay_triangulation_3 must define predicates to test for the empty sphere property. It is described by the concept DelaunayTriangulationTraits_3, which refines TriangulationTraits_3.
The kernels provided by CGAL: Cartesian, Homogeneous, Simple_cartesian, Simple_homogeneous and Filtered_kernel can all be used as models for the geometric traits parameter. They supply the user with all the functionalities described for the concepts TriangulationTraits_3 and DelaunayTriangulationTraits_3. In addition, the predefined kernels Exact_predicates_inexact_constructions_kernel and Exact_predicates_exact_constructions_kernel can also be used, the later being recommended when the dual construction is used.
In order to be used as the traits class for Regular_triangulation_3, a class must provide functions to compute the power tests (see Section 22.3). Regular_triangulation_euclidean_traits_3<K,Weight> is a traits class designed to be used by the class Regular_triangulation_3<RegularTriangulationTraits_3, TriangulationDataStructure_3>. It provides Weighted_point, a class for weighted points needed by the regular triangulation, which derives from the three dimensional point class K::Point_3. It supplies the user with all the functionalities described for the concept RegularTriangulationTraits_3. It can be used as a traits class for Regular_triangulation_3<RegularTriangulationTraits_3, TriangulationDataStructure_3>.
Note that for regular triangulations, plugging a filtered kernel such as Exact_predicates_inexact_constructions_kernel or Exact_predicates_exact_constructions_kernel in Regular_triangulation_euclidean_traits_3<K,Weight> will in fact not provide exact predicates since the weighted points and the predicates on them are not defined in the CGAL kernels. To solve this, there is also another model of the traits concept, Regular_triangulation_filtered_traits_3<FK>, which is providing filtered predicates (exact and efficient). The argument FK must be a model of the Kernel concept, and it is also restricted to be a instance of the Filtered_kernel template.
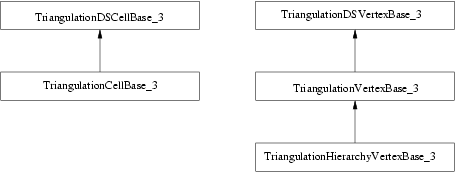
The second template parameter of the main classes (Triangulation_3, Delaunay_triangulation_3 and Regular_triangulation_3) is a triangulation data structure class. This class can be seen as a container for the cells and vertices maintaining incidence and adjacency relations (see Chapter 23). A model of this triangulation data structure is Triangulation_data_structure_3, and it is described by the TriangulationDataStructure_3 concept . This model is itself parameterized by a vertex base and a cell base classes, which gives the possibility to customize the vertices and cells used by the triangulation data structure, and hence by the geometric triangulation using it. Depending on the kind of triangulation used, the requirements on the vertex and cell base classes vary, and are expressed by various concepts, following the refinement diagram shown in Figure 22.5.2.
A default value for the triangulation data structure parameter is provided in all the triangulation classes, so it need not be specified by the user unless he wants to use a different triangulation data structure or a different vertex or cell base class.
In order to satisfy as many uses as possible, a design has been selected that allows to exchange different parts to meet the users' needs, while still re-using a maximum of the provided functionalities. We have already seen that the main triangulation classes are parameterized by a geometric traits class and a triangulation data structure (TDS), so that each of them can be interchanged with alternate implementations.
The most useful flexibility is the ability given to the user to add his own data in the vertices and cells by providing his own vertex and cell base classes to Triangulation_data_structure_3. The Figure 22.5.3 shows in more detail the flexibility that is provided, and the place where the user can insert his own vertex and/or cell base classes.
Starting with CGAL release 3.0, the design of the triangulation data structure has been changed in order to give the possibility to store handles (an entity akeen to pointers) directly in the vertex and cell base classes. Previously, void* pointers were stored there instead, and later converted internally to handles, but this happened to be too restrictive for some uses.
The difference is visible to the user when he provides his own vertex or cell base class. Previously, something like the following had to be written:
...
template < class GT >
class My_vertex
: public Triangulation_vertex_base<GT>
{
typedef Triangulation_vertex_base<GT> Vb;
public:
typedef typename Vb::Point Point;
My_vertex() {}
My_vertex(const Point&p) : Vb(p) {}
My_vertex(const Point&p, void *c) : Vb(p, c) {}
...
};
typedef Cartesian<double> GT;
typedef Triangulation_data_structure_3<My_vertex<GT>,
Triangulation_cell_base_3<GT> > My_TDS;
typedef Triangulation_3<GT, My_TDS> Tr;
...
While now, there are three possibilities. The simplest one is to use the class Triangulation_vertex_base_with_info_3, and this approach is illustrated in a following subsection 22.6.2.1. The most complicated one, and probably useless for almost all cases, is to write a vertex base class from scratch, following the documented requirements. This is mostly useless because most of the time it is enough to derive from the models that CGAL provides, and add the desired features. In this case, when the user needs to access some type that depends on the triangulation data structure (typically handles), then he should write something like:
...
template < class GT, class Vb = Triangulation_vertex_base<GT> >
class My_vertex
: public Vb
{
public:
typedef typename Vb::Point Point;
typedef typename Vb::Cell_handle Cell_handle;
template < class TDS2 >
struct Rebind_TDS {
typedef typename Vb::template Rebind_TDS<TDS2>::Other Vb2;
typedef My_vertex<GT, Vb2> Other;
};
My_vertex() {}
My_vertex(const Point&p) : Vb(p) {}
My_vertex(const Point&p, Cell_handle c) : Vb(p, c) {}
...
};
... // The rest has not changed
The changes that need to be made are the following:
The situation is exactly similar for cell base classes. Section 23.2 provides more detailed information.
// examples/Triangulation_3/example_simple.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Triangulation_3.h>
#include <iostream>
#include <fstream>
#include <cassert>
#include <list>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_3<K> Triangulation;
typedef Triangulation::Cell_handle Cell_handle;
typedef Triangulation::Vertex_handle Vertex_handle;
typedef Triangulation::Locate_type Locate_type;
typedef Triangulation::Point Point;
int main()
{
// construction from a list of points :
std::list<Point> L;
L.push_front(Point(0,0,0));
L.push_front(Point(1,0,0));
L.push_front(Point(0,1,0));
Triangulation T(L.begin(), L.end());
int n = T.number_of_vertices();
// insertion from a vector :
std::vector<Point> V(3);
V[0] = Point(0,0,1);
V[1] = Point(1,1,1);
V[2] = Point(2,2,2);
n = n + T.insert(V.begin(), V.end());
assert( n == 6 ); // 6 points have been inserted
assert( T.is_valid() ); // checking validity of T
Locate_type lt;
int li, lj;
Point p(0,0,0);
Cell_handle c = T.locate(p, lt, li, lj);
// p is the vertex of c of index li :
assert( lt == Triangulation::VERTEX );
assert( c->vertex(li)->point() == p );
Vertex_handle v = c->vertex( (li+1)&3 );
// v is another vertex of c
Cell_handle nc = c->neighbor(li);
// nc = neighbor of c opposite to the vertex associated with p
// nc must have vertex v :
int nli;
assert( nc->has_vertex( v, nli ) );
// nli is the index of v in nc
std::ofstream oFileT("output",std::ios::out);
// writing file output;
oFileT << T;
Triangulation T1;
std::ifstream iFileT("output",std::ios::in);
// reading file output;
iFileT >> T1;
assert( T1.is_valid() );
assert( T1.number_of_vertices() == T.number_of_vertices() );
assert( T1.number_of_cells() == T.number_of_cells() );
return 0;
}
// file: examples/Triangulation_3/example_color.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/Triangulation_vertex_base_with_info_3.h>
#include <CGAL/IO/Color.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_vertex_base_with_info_3<CGAL::Color, K> Vb;
typedef CGAL::Triangulation_data_structure_3<Vb> Tds;
typedef CGAL::Delaunay_triangulation_3<K, Tds> Delaunay;
typedef Delaunay::Point Point;
int main()
{
Delaunay T;
T.insert(Point(0,0,0));
T.insert(Point(1,0,0));
T.insert(Point(0,1,0));
T.insert(Point(0,0,1));
T.insert(Point(2,2,2));
T.insert(Point(-1,0,1));
// Set the color of finite vertices of degree 6 to red.
Delaunay::Finite_vertices_iterator vit;
for (vit = T.finite_vertices_begin(); vit != T.finite_vertices_end(); ++vit)
if (T.degree(vit) == 6)
vit->info() = CGAL::RED;
return 0;
}
// file: examples/Triangulation_3/example_adding_handles.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/Triangulation_vertex_base_3.h>
template < class GT, class Vb = CGAL::Triangulation_vertex_base_3<GT> >
class My_vertex_base
: public Vb
{
public:
typedef typename Vb::Vertex_handle Vertex_handle;
typedef typename Vb::Cell_handle Cell_handle;
typedef typename Vb::Point Point;
template < class TDS2 >
struct Rebind_TDS {
typedef typename Vb::template Rebind_TDS<TDS2>::Other Vb2;
typedef My_vertex_base<GT, Vb2> Other;
};
My_vertex_base() {}
My_vertex_base(const Point& p)
: Vb(p) {}
My_vertex_base(const Point& p, Cell_handle c)
: Vb(p, c) {}
Vertex_handle vh;
Cell_handle ch;
};
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_data_structure_3<My_vertex_base<K> > Tds;
typedef CGAL::Delaunay_triangulation_3<K, Tds> Delaunay;
typedef Delaunay::Vertex_handle Vertex_handle;
typedef Delaunay::Point Point;
int main()
{
Delaunay T;
Vertex_handle v0 = T.insert(Point(0,0,0));
Vertex_handle v1 = T.insert(Point(1,0,0));
Vertex_handle v2 = T.insert(Point(0,1,0));
Vertex_handle v3 = T.insert(Point(0,0,1));
Vertex_handle v4 = T.insert(Point(2,2,2));
Vertex_handle v5 = T.insert(Point(-1,0,1));
// Now we can link the vertices as we like.
v0->vh = v1;
v1->vh = v2;
v2->vh = v3;
v3->vh = v4;
v4->vh = v5;
v5->vh = v0;
return 0;
}
// file: examples/Triangulation_3/example_hierarchy.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/Triangulation_hierarchy_3.h>
#include <cassert>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_vertex_base_3<K> Vb;
typedef CGAL::Triangulation_hierarchy_vertex_base_3<Vb> Vbh;
typedef CGAL::Triangulation_data_structure_3<Vbh> Tds;
typedef CGAL::Delaunay_triangulation_3<K,Tds> Dt;
typedef CGAL::Triangulation_hierarchy_3<Dt> Dh;
typedef Dh::Vertex_iterator Vertex_iterator;
typedef Dh::Vertex_handle Vertex_handle;
typedef Dh::Point Point;
int main()
{
Dh T;
// insertion of points on a 3D grid
std::vector<Vertex_handle> V;
for (int z=0 ; z<5 ; z++)
for (int y=0 ; y<5 ; y++)
for (int x=0 ; x<5 ; x++)
V.push_back(T.insert(Point(x,y,z)));
assert( T.is_valid() );
assert( T.number_of_vertices() == 125 );
assert( T.dimension() == 3 );
// removal of the vertices in random order
std::random_shuffle(V.begin(), V.end());
for (int i=0; i<125; ++i)
T.remove(V[i]);
assert( T.is_valid() );
assert( T.number_of_vertices() == 0 );
return 0;
}
// file: examples/Triangulation_3/example_find_conflicts.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/point_generators_3.h>
#include <vector>
#include <cassert>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Delaunay_triangulation_3<K> Delaunay;
typedef Delaunay::Point Point;
typedef Delaunay::Cell_handle Cell_handle;
typedef Delaunay::Facet Facet;
int main()
{
Delaunay T;
CGAL::Random_points_in_sphere_3<Point> rnd;
// First, make sure the triangulation is 3D.
T.insert(Point(0,0,0));
T.insert(Point(1,0,0));
T.insert(Point(0,1,0));
T.insert(Point(0,0,1));
assert(T.dimension() == 3);
// Inserts 100 random points if and only if their insertion
// in the Delaunay tetrahedralization conflicts with
// an even number of cells.
for (int i = 0; i != 100; ++i) {
Point p = *rnd++;
// Locate the point
Delaunay::Locate_type lt;
int li, lj;
Cell_handle c = T.locate(p, lt, li, lj);
if (lt == Delaunay::VERTEX)
continue; // Point already exists
// Get the cells that conflict with p in a vector V,
// and a facet on the boundary of this hole in f.
std::vector<Cell_handle> V;
Facet f;
T.find_conflicts(p, c,
CGAL::Oneset_iterator<Facet>(f), // Get one boundary facet
std::back_inserter(V)); // Conflict cells in V
if ((V.size() & 1) == 0) // Even number of conflict cells ?
T.insert_in_hole(p, V.begin(), V.end(), f.first, f.second);
}
std::cout << "Final triangulation has " << T.number_of_vertices()
<< " vertices." << std::endl;
return 0;
}
// file: examples/Triangulation_3/example_regular.C
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Regular_triangulation_3.h>
#include <CGAL/Regular_triangulation_euclidean_traits_3.h>
#include <CGAL/Regular_triangulation_filtered_traits_3.h>
#include <cassert>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Regular_triangulation_filtered_traits_3<K> Traits;
typedef Traits::RT Weight;
typedef Traits::Bare_point Point;
typedef Traits::Weighted_point Weighted_point;
typedef CGAL::Regular_triangulation_3<Traits> Rt;
typedef Rt::Vertex_iterator Vertex_iterator;
typedef Rt::Vertex_handle Vertex_handle;
int main()
{
Rt T;
// insertion of points on a 3D grid
std::vector<Vertex_handle> V;
for (int z=0 ; z<5 ; z++)
for (int y=0 ; y<5 ; y++)
for (int x=0 ; x<5 ; x++) {
Point p(x, y, z);
Weight w = (x+y-z*y*x)*2.0; // let's say this is the weight.
Weighted_point wp(p, w);
V.push_back(T.insert(wp));
}
assert( T.is_valid() );
assert( T.dimension() == 3 );
std::cout << "Number of vertices : " << T.number_of_vertices() << std::endl;
return 0;
}
Monique Teillaud started to work on the 3D triangulation packages in 1997, following the design of the 2D triangulation packages. The notions of degenerate dimensions and infinite vertex were formalized [Tei99] and induced changes in the 2D triangulation packages. The packages were first released in CGAL 2.1. They contained basic functionalities on triangulations, Delaunay triangulations, regular triangulations.
A first version of removal of a vertex from a Delaunay triangulation was released in CGAL 2.2. However, this removal became really robust only in CGAL 2.3, after some research that allowed to deal with degenerate cases quite easily [DT03]. Andreas Fabri implemented this revised version of the removal, and a faster removal algorithm for CGAL 3.0.
In 2000, Sylvain Pion started working on these packages. He improved the efficiency of triangulations in CGAL 2.3 and 2.4 in several ways [BDP02]: he implemented the Delaunay hierarchy [Dev02] in 2.3, he improved the memory footprint in 2.4 and 3.0, he also performed work on arithmetic filters [DP03] (see Support Library and Kernel) to improve the speed of triangulations. He changed the design in CGAL 3.0, allowing users to add handles in their own vertices and cells.
In 2005, Christophe Delage implemented the vertex removal function for regular triangulations, which allowed to release this functionality in CGAL 3.2.
The authors also wish to thank Jean-Daniel Boissonnat, Olivier Devillers and Mariette Yvinec for helpful discussions [BDTY00].