CGAL::Regular_triangulation_3<RegularTriangulationTraits_3,TriangulationDataStructure_3>

Definition

³

p^(w)=(p,w_p), p ³, w_p

z^(w)=(z,w_z), z ³, w_z

$$(p^(w),z^(w)) = p-z ²-w_p-w_z

where $$ p-z is the Euclidean distance between $$p and $$z. $$p^(w) and $$z^(w) are said to be orthogonal if $$(p^(w)-z^(w)) = 0 (see Figure 22.3).

Four weighted points have a unique common orthogonal weighted point called the power sphere. A sphere $$z^(w) is said to be regular if $$ p^(w) S^(w), (p^(w)-z^(w)) 0.

A triangulation of $$S^(w) is regular if the power spheres of all simplices are regular.

#include <CGAL/Regular_triangulation_3.h>

Parameters

The first template argument must be a model of the RegularTriangulationTraits_3 concept.

The second template argument must be a model of the TriangulationDataStructure_3 concept. It has the default value Triangulation_data_structure_3<Triangulation_vertex_base_3<RegularTriangulationTraits_3>, Triangulation_cell_base_3<RegularTriangulationTraits_3> >.

Inherits From

Types

typedef RegularTriangulationTraits_3::Bare_point
	Bare_point;	The type for points p of weighted points $$p(w)=(p,wp)
typedef RegularTriangulationTraits_3::Weighted_point_3
	Weighted_point;

Creation

Regular_triangulation_3<RegularTriangulationTraits_3,TriangulationDataStructure_3> rt ( RegularTriangulationTraits_3 traits = RegularTriangulationTraits_3());
	Creates an empty regular triangulation, possibly specifying a traits class traits.
Regular_triangulation_3<RegularTriangulationTraits_3,TriangulationDataStructure_3> rt ( Regular_triangulation_3 rt1);
	Copy constructor.
template < class InputIterator >
Regular_triangulation_3<RegularTriangulationTraits_3,TriangulationDataStructure_3> rt ( InputIterator first, InputIterator last, RegularTriangulationTraits_3 traits = RegularTriangulationTraits_3());
	Creates a regular triangulation of the points specified by the iterator range [first,last) of value type Weighted_point, possibly specifying a traits class traits.

Operations

Insertion

The following methods, which already exist in triangulations, are overloaded to ensure the property that all power spheres are regular.

Vertex_handle	rt.insert ( Weighted_point p, Cell_handle start = Cell_handle())
		Inserts weighted point p in the triangulation. If this insertion creates a vertex, this vertex is returned. Otherwise, this method returns the default constructed handle. If p coincides with an existing vertex and has a greater weight, then p replaces that point and the triangulation is updated. The optional argument start is used as a starting place for the search.
Vertex_handle	rt.insert ( Weighted_point p, Locate_type lt, Cell_handle loc, int li, int lj)
		Inserts weighted point p in the triangulation and returns the corresponding vertex. Similar to the above insert() function, but takes as additional parameter the return values of a previous location query. See description of Triangulation_3::locate().

The following method allows one to insert several points.

template < class InputIterator >
int	rt.insert ( InputIterator first, InputIterator last)
		Inserts the weighted points in the range $$[.first, last$$.). It returns the difference of the number of vertices between after and before the insertions (it may be negative due to hidden points). Precondition: The value_type of first and last is Point.

Removal

void	rt.remove ( Vertex_handle v)
		Removes the vertex v from the triangulation.

Queries

Let us remark that

$$(p^(w)-z^(w)) > 0

is equivalent to

Figure:  side_of_power_circle.

Bounded_side	rt.side_of_power_sphere ( Cell_handle c, Weighted_point p)
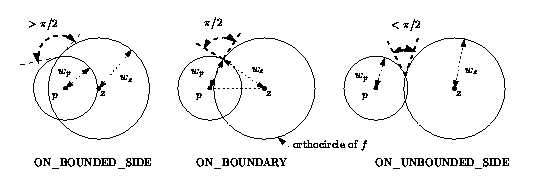
		Returns the position of the weighted point $$p with respect to the power sphere of c. More precisely, it returns: - ON_BOUNDED_SIDE if $$(p(w)-z(c)(w))<0 where $$z(c)(w) is the power sphere of c. For an infinite cell this means either that p lies strictly in the half space limited by its finite facet and not containing any other point of the triangulation, or that the angle between p and the power circle of the finite facet of c is greater than $$/2. - ON_BOUNDARY if p is orthogonal to the power sphere of c i.e. $$(p(w)-z(c)(w))=0. For an infinite cell this means that p is orthogonal to the power circle of its finite facet. - ON_UNBOUNDED_SIDE if $$(p(w)-z(c)(w))>0 i.e. the angle between the weighted point p and the power sphere of c is less than $$/2 or if these two spheres do not intersect. For an infinite cell this means that p does not satisfy either of the two previous conditions. Precondition: rt.dimension() $$=3.
Bounded_side	rt.side_of_power_circle ( Facet f, Weighted_point p)
		Returns the position of the point p with respect to the power circle of f. More precisely, it returns: - in dimension 3: - For a finite facet, ON_BOUNDARY if p is orthogonal to the power circle in the plane of the facet, ON_UNBOUNDED_SIDE when their angle is less than $$/2, ON_BOUNDED_SIDE when it is greater than $$/2 (see Figure 22.9). - For an infinite facet, it considers the plane defined by the finite facet of the cell f.first, and does the same as in dimension 2 in this plane. - in dimension 2: - For a finite facet, ON_BOUNDARY if p is orthogonal to the circle, ON_UNBOUNDED_SIDE when the angle between p and the power circle of f is less than $$/2, ON_BOUNDED_SIDE when it is greater than $$/2. - For an infinite facet, ON_BOUNDED_SIDE for a point in the open half plane defined by f and not containing any other point of the triangulation, ON_UNBOUNDED_SIDE in the other open half plane. If the point p is collinear with the finite edge e of f, it returns: ON_BOUNDED_SIDE if $$(p(w)-z(e)(w))<0, where $$z(e)(w) is the power segment of e in the line supporting e, ON_BOUNDARY if $$(p(w)-z(e)(w))=0, ON_UNBOUNDED_SIDE if $$(p(w)-z(e)(w))>0 . Precondition: rt.dimension() $$ 2.
Bounded_side	rt.side_of_power_circle ( Cell_handle c, int i, Weighted_point p)
		Same as the previous method for facet i of cell c.
Bounded_side	rt.side_of_power_segment ( Cell_handle c, Weighted_point p)
		In dimension 1, returns ON_BOUNDED_SIDE if $$(p(w)-z(c)(w))<0, where $$z(c)(w) is the power segment of the edge represented by c, ON_BOUNDARY if $$(p(w)-z(c)(w))=0, ON_UNBOUNDED_SIDE if $$(p(w)-z(c)(w))>0 . Precondition: rt.dimension() $$= 1.
Vertex_handle	rt.nearest_power_vertex ( Point p, Cell_handle c = Cell_handle())
		Returns the vertex of the triangulation which is nearest to $$p with respect to the power distance. This means that the power of the query point p with respect to the weighted point in the returned vertex is smaller than the power of p with respect to the weighted point in any other vertex. Ties are broken arbitrarily. The default constructed handle is returned if the triangulation is empty. The optional argument c is a hint specifying where to start the search. Precondition: c is a cell of rt.
Vertex_handle	rt.nearest_power_vertex_in_cell ( Point p, Cell_handle c)
		Returns the vertex of the cell c that is nearest to $$p with respect to the power distance.

A weighted point p is said to be in conflict with a cell c in dimension 3 (resp. with a facet f in dimension 2) if it has a negative power distance to the power sphere of c (resp. to the power circle of f). The set of cells (resp. facets in dimension 2) which are in conflict with p is connected.

template <class OutputIteratorBoundaryFacets, class OutputIteratorCells, class OutputIteratorInternalFacets>
Triple<OutputIteratorBoundaryFacets, OutputIteratorCells, OutputIteratorInternalFacets>
	rt.find_conflicts ( const Weighted_point p, Cell_handle c, OutputIteratorBoundaryFacets bfit, OutputIteratorCells cit, OutputIteratorInternalFacets ifit)
		Compute the conflicts with p. The starting cell (resp. facet) c must be in conflict with p. Then this function returns respectively in the output iterators: - cit: the cells (resp. facets) in conflict with p. - bfit: the facets (resp. edges) on the boundary of the conflict zone, that is, the facets (resp. edges) (t, i) where the cell (resp. facet) t is in conflict, but t->neighbor(i) is not. - ifit: the facets (resp. edges) inside the conflict zone, that facets incident to two cells (resp facets) in conflict. Returns the Triple composed of the resulting output iterators. Precondition: rt.dimension() $$ 2, and c is in conflict with p.

In the weighted setting, a face (cell, facet, edge or vertex) is said to be a Gabriel face iff the smallest sphere orthogonal to the weighted points associated to its vertices, has a positive power product with the weighted point of any other vertex of the triangulation. Any weighted Gabriel face belongs to the regular triangulation, but the reciprocal is not true. The following member functions test the Gabriel property of the faces of the regular triangulation.

bool	rt.is_Gabriel ( Cell_handle c, int i)
bool	rt.is_Gabriel ( Cell_handle c, int i, int j)
bool	rt.is_Gabriel ( Facet f)
bool	rt.is_Gabriel ( Edge e)
bool	rt.is_Gabriel ( Vertex_handle v)

Power diagram

Note that the user should use a kernel with exact constructions in order to guarantee the computation of the Voronoi diagram (as opposed to computing the triangulation only, which requires only exact predicates).

Point	rt.dual ( Cell_handle c)
		Returns the weighted circumcenter of the four vertices of c. Precondition: rt.dimension()$$=3 and c is not infinite.
Object	rt.dual ( Facet f)	Returns the dual of facet f, which is in dimension 3: either a segment, if the two cells incident to f are finite, or a ray, if one of them is infinite; in dimension 2: a point. Precondition: rt.dimension() $$ 2 and f is not infinite.
Object	rt.dual ( Cell_handle c, int i)
		same as the previous method for facet (c,i).
template <class Stream>
Stream &	rt.draw_dual ( Stream & os)
		Sends the set of duals to all the facets of rt into os.

advanced

Checking

bool	rt.is_valid ( bool verbose = false)
		Checks the combinatorial validity of the triangulation and the validity of its geometric embedding (see Section 22.1). Also checks that all the power spheres (resp. power circles in dimension 2, power segments in dimension 1) of cells (resp. facets in dimension 2, edges in dimension 1) are regular. When verbose is set to true, messages describing the first invalidity encountered are printed. This method is mainly a debugging help for the users of advanced features.

advanced