Chapter 61
Linear and Quadratic Programming Solver

Table of Contents

61.1   Which Programs can be Solved?

(QP)$$	minimize$$	xTDx+cTx+c0
	subject to$$	Ax ~ b,
		l x u

in $$n real variables $$x=(x₀,...,x_n-1). Here,

• $$A is an $$m × n matrix (the constraint matrix),
• $$b is an $$m-dimensional vector (the right-hand side),
• $$ ~  is an $$m-dimensional vector of relations from $${ , =, },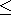
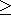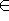
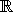
• $$l is an $$n-dimensional vector of lower bounds for $$x, where $$l_j {- } for all 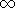$$j
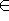
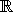
• $$u is an $$n-dimensional vector of upper bounds for $$x, where $$u_j { } for all 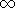$$j
• $$D is a symmetric positive-semidefinite $$n × n matrix (the quadratic objective function),
• $$c is an $$n-dimensional vector (the linear objective function), and
• $$c₀ is a constant.

If $$D=0, the program (QP) is actually a linear program. Section 61.2.2 on robustness briefly discusses the case of $$D not being positive-semidefinite and therefore not defining a convex program.

Solving the program means to find an $$n-vector $$x^* such that $$Ax^* ~ b, l x^* u (a feasible solution), and with the smallest objective function value $$x^*TDx^*+c^Tx^*+c₀ among all feasible solutions.

There might be no feasible solution at all, in which case the quadratic program is infeasible, or there might be feasible solutions of arbitrarily small objective function value, in which case the program is unbounded.

61.2   Design, Efficiency, and Robustness

Then the program is solved using the function solve_quadratic_program (or some specialized other functions, e.g. for linear programs). For this, you also have to provide a suitable exact number type ET used in the solution process. In case of input type double, solution methods that use floating-point-filtering are chosen by default for certain programs (in some cases, this is not appropriate, and the default should be changed; see Section 61.8 for details).

The output of this is an object of Quadratic_program_solution<ET> which you can in turn query for various things: what is the status of the program (optimally solved, infeasible, or unbounded?), what are the values of the optimal solution $$x^*, what is the associated objective function value, etc.

You can in particular get certificates for the solution. In short, these are proofs that the output is correct. Thus, if you don't believe in the solution (whether it says ``optimally solved'', ``infeasible'', or ``unbounded''), you can verify it yourself by using the certificates. Section 61.7 says more about this.

61.2.1   Efficiency

This has mainly historical reasons: the original motivation behind this package was low-dimensional geometric optimization where a dense representation is appropriate and efficient. In fact, the CGAL packages Min_annulus_d<Traits> and Polytope_distance_d<Traits> internally use the linear and quadratic programming solver.

As a user, however, you don't necessarily have to provide a dense representation of your program. You do not pass vectors or matrices to the solution functions, but rather specify the vectors and matrices through iterators. The iterator abstraction easily allows to build models that convert a sparse representation into a dense interface. The predefined models Quadratic_program<NT> and Quadratic_program_from_mps<NT> do exactly this; in using them, you can forget about the dense interface.

Nevertheless, if you care about efficiency, you cannot completely ignore the issue. If you think about a quadratic program in $$n variables and $$m constraints, its dense interface has $$(n² + mn) entries, even if actually very few of them are nonzero. This has consequences for the complexity of the internal computations. In fact, a single iteration of the solution process has complexity at least $$(mn), since usually, all entries of the matrix $$A are accessed. This implies that problems where $$min$$(n,m) is large cannot be solved efficiently, even if the number of nonzero entries in the problem description is very small.

We can actually be quite precise about performance, in terms of the following parameters.

The time required to solve the problems is in most cases linear in $$max$$(n,m), but with a factor heavily depending on $$min$$(n,e)+r. Therefore, the solver will be efficient only if $$min$$(n,e)+r is small.

Here are the scenarios in which this applies:

• Quadratic programs with a small number of variables, but possibly a large number of inequality constraints,
• Linear programs with a small number of equality constraints but possibly a large number of variables,
• Quadratic programs with a small number of equality constraints and $$D of small rank, but possibly with a large number of variables.

How small is small? If $$min$$(n,e)+r is up to $$10, the solver will probably be very fast, even if $$max$$(n,m) goes into the millions. If $$min$$(n,m)+r is up to a few hundreds, you may still get a solution within reasonable time, depending on the problem characteristics.

If you have a problem where both $$n and $$e are well above $$1,000, say, then chances are high that CGAL cannot solve it within reasonable time.

61.2.2   Robustness

1. The quadratic program is too large (see the previous subsection on efficiency).
2. The quadratic objective function matrix $$D is not positive-semidefinite (see the discussion below).
3. The floating-point filter used by default for certain programs and input type double fails due to a double exponent overflow. This happens in rare cases only, and it does not pay off to sacrifice the efficiency of the filtered approach in order to cope with these rare cases. There are means, however, to avoid such problems by switching to a slower non-filtered variant, see Section 61.8.1.
4. The solver internally cycles. This also happens in rare cases only. However, if you have a hunch that the solver cycles on your problem, there are means to switch to a slower variant that is guaranteed not to cycle, see Section 61.8.2.

The second item merits special attention. First, you may ask why the solver does not check that $$D is positive semidefinite. But recall that $$D is given by a dense interface, and it would therefore cost $$(n²) time already to access all entries of the matrix $$D. The solver itself gets away with accessing much less entries of $$D in the relevant case where $$r, the rank of $$D, is small.

Nevertheless, the solver contains some runtime checks that may detect that the matrix $$D is not positive-semidefinite. But you may as well get an ``optimal solution'' in this case, even with valid certificates. The validity of these certificates, however, depends on $$D being positive-semidefinite; if this is not the case, the certificates only prove that the solver has found a ``critical point'' of your (nonconvex) program, but there are no guarantees whatsoever that this is a global optimum, or even a local optimum.

61.3   How to Enter and Solve a Program

• you can let the model take care of your program data; you start from an empty program and then simply insert the non-zero entries, or read them from a file (more generally, any input stream) in MPSFormat. You can also change program entries at any time. This is usually the most convenient way if you don't want to care about representation issues;
• you can maintain the data yourself and only supply suitable random-access iterators over the matrices and vectors. This is advantageous if you already have the data (explicitly, or implicitly encoded, for example through iterators) and want to avoid copying of data. Typically, this happens if you write generic iterator-based code.

Our running example is the following quadratic program in two variables:

minimize$$	x2 + 4(y-4)2	(=	x2 + 4y2 - 32y + 64)
subject to$$	x + y		7
	-x + 2y		4
	x		0
	y		0
	y		4

Figure 61.1 shows a picture. It depicts the five inequalities of the program, along with the feasible region (green), the set of points that satisfy all the five constraints. The dashed elliptic curves represent contour lines of the objective function, i.e., along each dashed curve, the objective function value is constant.

The global minimum of the objective function is attained at the point $$(0,4), and the minimum within the feasible region appears at the point $$(2,3) marked with a black dot. The value of the objective function at this optimal solution is $$2² + 4(3-4)² = 8.

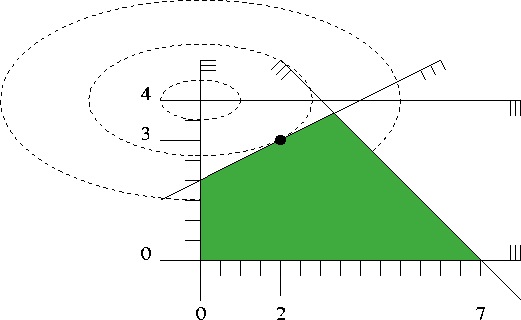
Figure 61.1:  A quadratic program in two variables

61.3.1   Constructing a Program from Data

For examples how to work with the input type double, we refer to Sections 61.5 and 61.8.

Note: For the quadratic objective function, the entries of the matrix $$2D have to be provided, rather than $$D. Although this is common to almost all quadratic programming solvers, it can easily be overlooked by a novice.

File: examples/QP_solver/first_qp.cpp

#include <iostream>
#include <cassert>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

// program and solution types
typedef CGAL::Quadratic_program<int> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;

int main() {
  // by default, we have a nonnegative QP with Ax <= b
  Program qp (CGAL::SMALLER, true, 0, false, 0); 
  
  // now set the non-default entries: 
  const int X = 0; 
  const int Y = 1;
  qp.set_a(X, 0,  1); qp.set_a(Y, 0, 1); qp.set_b(0, 7);  //  x + y  <= 7
  qp.set_a(X, 1, -1); qp.set_a(Y, 1, 2); qp.set_b(1, 4);  // -x + 2y <= 4
  qp.set_u(Y, true, 4);                                   //       y <= 4
  qp.set_d(X, X, 2); qp.set_d (Y, Y, 8); // !!specify 2D!!    x^2 + 4 y^2
  qp.set_c(Y, -32);                                       // -32y
  qp.set_c0(64);                                          // +64

  // solve the program, using ET as the exact type
  Solution s = CGAL::solve_quadratic_program(qp, ET());
  assert (s.solves_quadratic_program(qp));

  // output solution
  std::cout << s; 
  return 0;
}

Asuming that GMP is installed, the output of the of the above program is:

status:          OPTIMAL
objective value: 8/1
variable values:
  0: 2/1
  1: 3/1

61.3.2   Constructing a Program from a Stream

File: examples/QP_solver/first_qp_from_mps.cpp

#include <iostream>
#include <fstream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

// program and solution types
typedef CGAL::Quadratic_program_from_mps<int> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;

int main() {
  std::ifstream in ("first_qp.mps");
  Program qp(in);         // read program from file
  assert (qp.is_valid()); // we should have a valid mps file

  // solve the program, using ET as the exact type
  Solution s = CGAL::solve_quadratic_program(qp, ET());

  // output solution
  std::cout << s; 
  return 0;
}

61.3.3   Constructing a Program from Iterators

File: examples/QP_solver/first_qp_from_iterators.cpp

#include <iostream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

// program and solution types
typedef CGAL::Quadratic_program_from_iterators
<int**,                                                // for A
 int*,                                                 // for b
 CGAL::Const_oneset_iterator<CGAL::Comparison_result>, // for r
 bool*,                                                // for fl
 int*,                                                 // for l
 bool*,                                                // for fu
 int*,                                                 // for u
 int**,                                                // for D
 int*>                                                 // for c 
Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;

int main() {
  int  Ax[] = {1, -1};                        // column for x
  int  Ay[] = {1,  2};                        // column for y
  int*  A[] = {Ax, Ay};                       // A comes columnwise
  int   b[] = {7, 4};                         // right-hand side
  CGAL::Const_oneset_iterator<CGAL::Comparison_result> 
        r(    CGAL::SMALLER);                 // constraints are "<="
  bool fl[] = {true, true};                   // both x, y are lower-bounded
  int   l[] = {0, 0};
  bool fu[] = {false, true};                  // only y is upper-bounded
  int   u[] = {0, 4};                         // x's u-entry is ignored
  int  D1[] = {2};                            // 2D_{1,1}
  int  D2[] = {0, 8};                         // 2D_{2,1}, 2D_{2,2}
  int*  D[] = {D1, D2};                       // D-entries on/below diagonal
  int   c[] = {0, -32};
  int  c0   = 64;                             // constant term

  // now construct the quadratic program; the first two parameters are
  // the number of variables and the number of constraints (rows of A)
  Program qp (2, 2, A, b, r, fl, l, fu, u, D, c, c0);

  // solve the program, using ET as the exact type
  Solution s = CGAL::solve_quadratic_program(qp, ET());

  // output solution
  std::cout << s;
  return 0;
}

Note 1: The example shows an interesting feature of this approach: not all data need to come from containers. Here, the iterator over the vector of relations can be provided through the class Const_oneset_iterator<T>, since all entries of this vector are equal to CGAL::SMALLER. The same could have been done with the vector fl for the finiteness of the lower bounds.

Note 2: The program type looks a bit scary, with its total of 9 template arguments, one for each iterator type. In Section 61.5.1 we show how the explicit construction of this type can be circumvented.

61.4   Solving Linear and Nonnegative Programs

From an interface perspective, this is just syntactic sugar: in the model Quadratic_program<NT>, we can easily set the default bounds so that a nonnegative program results, and a linear program is obtained by simply not inserting any $$D-entries. Even in the iterator-based approach (see QP_solver/first_qp_from_iterators.cpp), linear and nonnegative programs can easily be defined through suitable Const_oneset_iterator<T>-style iterators.

The main reason for having dedicated solution methods for linear and nonnegative programs is efficiency: if the solver knows that the program is linear, it can save some computations compared to the general solver that unknowingly has to fiddle around with a zero $$D-matrix. As in Section 61.2.2 above, we can argue that checking in advance whether $$D=0 is not an option in general, since this may require $$(n²) time on the dense interface.

Similarly, if the solver knows that the program is nonnegative, it will be more efficient than under the general bounds $$l x u. You can argue that nonnegativity is something that could easily be checked in time $$O(n) beforehand, but then again nonnegative programs are so frequent that the syntactic sugar aspect becomes somewhat important. After all, we can save four iterators in specifying a nonnegative linear program in terms of the concept NonnegativeLinearProgram rather than LinearProgram.

Often, there are no bounds at all for the variables, i.e., all entries of $$l are $$- , and all entries of $$u are $$ (this is called a free program). There is no dedicated solution method for this case (a free quadratic or linear program is treated like a general quadratic or linear program), but all predefined models make it easy to specify all sorts of default bounds, covering the free case.

61.4.1   The Linear Programming Solver

minimize$$	- 32y + 64
subject to$$	x + y		7
	-x + 2y		4
	x		0
	y		0
	y		4

Figure 61.2 shows how this looks like. We will not visualize a linear objective function with contour lines but with arrows instead. The arrow represents the (direction) of the vector $$-c, and we are looking for a feasible solution that is ``extreme'' in the direction of the arrow. In our small example, this is the unique point ``on'' the two constraints $$x₁+x₂ 7 and $$-x₁+x₂ 4, the point $$(10/3,11/3) marked with a black dot. The optimal objective function value is $$-32(11/3)+64=-160/3.

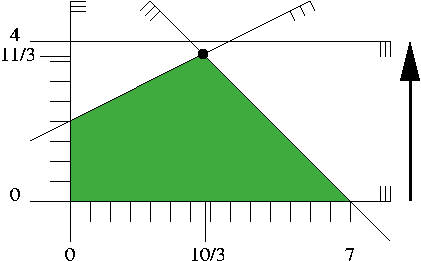
Figure 61.2:  A linear program in two variables

Here is CGAL code for solving it, using the dedicated LP solver, and according to the three ways for constructing a program that we have already discussed in Section 61.3.

QP_solver/first_lp.cpp
QP_solver/first_lp_from_mps.cpp
QP_solver/first_lp_from_iterators.cpp

In all cases, the output is

status:          OPTIMAL
objective value: -160/3
variable values:
  0: 10/3
  1: 11/3

61.4.2   The Nonnegative Quadratic Programming Solver

y 4

minimize$$	x2 + 4(y-4)2	(=	x2 + 4y2 - 32y + 64)
subject to$$	x + y		7
	-x + 2y		4
	x,y		0

Figure 61.3 contains the illustration; since the constraint $$y 4 was redundant, the feasible region and the optimal solution do not change.

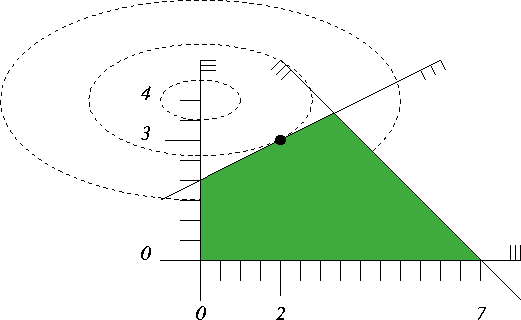
Figure 61.3:  A nonnegative quadratic program in two variables

The following programs (using the dedicated solver for nonnegative quadratic programs) will therefore again output

status:          OPTIMAL
objective value: 8/1
variable values:
  0: 2/1
  1: 3/1

QP_solver/first_nonnegative_qp.cpp
QP_solver/first_nonnegative_qp_from_mps.cpp
QP_solver/first_nonnegative_qp_from_iterators.cpp

61.4.3   The Nonnegative Linear Programming Solver

y 4

minimize$$	- 32y
subject to$$	x + y		7
	-x + 2y		4
	x,y		0

This can be solved by any of the following three programs

QP_solver/first_nonnegative_lp.cpp
QP_solver/first_nonnegative_lp_from_mps.cpp
QP_solver/first_nonnegative_lp_from_iterators.cpp

The output will always be

status:          OPTIMAL
objective value: -352/3
variable values:
  0: 10/3
  1: 11/3

61.5   Working from Iterators

The problem we are going to solve is the following: given points $$p₁,...p_n in $$d-dimensional space and another point $$p: is $$p in the convex hull of $${p₁,...,p_n}? In formulas, this is the case if and only if there are real coefficients $$₁,...,_n such that $$p is a convex combination of $$p₁,...,p_n:

$$ p = _j=1ⁿ _j p_j,    _j=1ⁿ _j = 1,   _j 0  for all $$j.$$

The problem of testing the existence of such $$_j can be expressed as a linear program. It becomes particularly easy when we use the homogeneous representations of the points: if $$q₁,...,q_n,q ^d+1 are homogeneous coordinates for $$p₁,...,p_n,p with positive homogenizing coordinates $$h₁,...,h_n,h, we have

$$q_j = h_j · (p_j 1)  for all $$j, and $$ q = h · (p 1).

Now, nonnegative $$₁,...,_n are suitable coefficients for a convex combination if and only if

$$ _j=1ⁿ  _j(p_j 1) = (p 1),

equivalently, if there are $$µ₁,...,µ_n (with $$µ_j = _j · h/h_j for all $$j) such that

$$ _j=1ⁿ µ_j q_j = q,   µ_j 0 for all $$j$$.

The linear program now tests for the existence of nonnegative $$µ_j that satisfy the latter equation. Below is the code; it defines a function that solves the linear program, given $$p and $$p₁,...,p_n (through an iterator range). The only (mild) trickery involved is the construction of the nested iterator through a fixed column of the constraint matrix $$A. We get this from transforming the iterator through the points using a functor that maps a point to an iterator through its homogeneous coordinates.

File: examples/QP_solver/solve_convex_hull_containment_lp.h

#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin  {
  typedef typename Point_d::Homogeneous_const_iterator result_type;
  result_type operator() (const Point_d& p) const {
    return p.homogeneous_begin();
  }
};

// function to solve the LP that tests whether a point is in the
// convex hull of other points; the type ET is an exact type used
// for the internal computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
				  RandomAccessIterator begin,
				  RandomAccessIterator end, const ET& dummy)
{
  // Constraint matrix type: A[j][i] is the i-th homogeneous coordinate of p_j
  typedef boost::transform_iterator
    <Homogeneous_begin<Point_d>, RandomAccessIterator> A_it;
  // Right-hand side type: b[i] is the i-th homogeneous coordinate of p
  typedef typename Point_d::Homogeneous_const_iterator B_it;
  // Relation type ("=")
  typedef CGAL::Const_oneset_iterator<CGAL::Comparison_result> R_it;
  // input number type
  typedef typename CGAL::Kernel_traits<Point_d>::Kernel::RT RT;
  // Linear objective function type (c=0: we only test feasibility)
  typedef CGAL::Const_oneset_iterator<RT> C_it;
  // the nonnegative linear program type
  typedef
    CGAL::Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it>
    Program;

  // ok, we are prepared now: construct program and solve it
  Program lp (end-begin,        // number of variables
	      p.dimension()+1,  // number of constraints
	      A_it (begin), B_it (p.homogeneous_begin()),
	      R_it (CGAL::EQUAL), C_it (0));
  return CGAL::solve_nonnegative_linear_program (lp, dummy);
}

To see this in action, let us call it with $$p₁=(0,0), p₂=(10,0), p₃=(0,10) fixed (they define a triangle) and all integral points $$p in $$[0,10]². We know that $$p is in the convex hull of $${p₁,p₂,p₃} if and only if its two coordinates sum up to $$10 at most. As the exact type, we use MP_Float or Gmpzf (which is faster and preferable if GMP is installed).

File: examples/QP_solver/convex_hull_containment.cpp

#include <cassert>
#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include "solve_convex_hull_containment_lp.h"

// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;

bool is_in_convex_hull (const Point_d& p,
			std::vector<Point_d>::const_iterator begin,
			std::vector<Point_d>::const_iterator end)
{
  CGAL::Quadratic_program_solution<ET> s =
    solve_convex_hull_containment_lp (p, begin, end, ET(0));
  return !s.is_infeasible();
}

int main()
{
  std::vector<Point_d> points;
  // convex hull: simplex spanned by {(0,0), (10,0), (0,10)}
  points.push_back (Point_d ( 0.0,  0.0));
  points.push_back (Point_d (10.0,  0.0));
  points.push_back (Point_d ( 0.0, 10.0));
  for (int i=0; i<=10; ++i)
    for (int j=0; j<=10; ++j) {
      // (i,j) is in the simplex iff i+j <= 10
      bool contained = is_in_convex_hull
	(Point_d (i, j), points.begin(), points.end());
      assert (contained == (i+j<=10));
    }

  return 0;
}

61.5.1   Using Makers

You can avoid the explicit construction of the type CGAL::Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it> if you only need an expression of it, e.g. to pass it directly as an argument to the solving function. Here is an alternative version of QP_solver/solve_convex_hull_containment_lp.h that shows how this works. In effect, you get shorter and more readable code.

File: examples/QP_solver/solve_convex_hull_containment_lp2.h

#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin  {
  typedef typename Point_d::Homogeneous_const_iterator result_type;
  result_type operator() (const Point_d& p) const {
    return p.homogeneous_begin();
  }
};

// function to test whether point is in the convex hull of other points;
// the type ET is an exact type used for the computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
				  RandomAccessIterator begin,
				  RandomAccessIterator end, const ET& dummy)
{
  // construct program and solve it
  return CGAL::solve_nonnegative_linear_program
    (CGAL::make_nonnegative_linear_program_from_iterators
     (end-begin,                                                           // n
      p.dimension()+1,                                                     // m
      boost::transform_iterator
      <Homogeneous_begin<Point_d>, RandomAccessIterator>(begin),           // A
      typename Point_d::Homogeneous_const_iterator (p.homogeneous_begin()),// b
      CGAL::Const_oneset_iterator<CGAL::Comparison_result>(CGAL::EQUAL),   // ~
      CGAL::Const_oneset_iterator
      <typename CGAL::Kernel_traits<Point_d>::Kernel::RT> (0)), dummy);    // c
}

61.6   Important Variables and Constraints

The following example shows how we can access the important variables, using the iterators basic_variable_indices_begin() and basic_variable_indices_end().

We generate a set of points that form a 4-gon in $$[0,4]², and then find the ones that contribute to the convex combinations of all 25 lattice points in $$[0,4]². If the lattice point in question is not in the 4-gon, we simply output this fact.

File: examples/QP_solver/important_variables.cpp

#include <cassert>
#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include "solve_convex_hull_containment_lp2.h"

typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;
typedef CGAL::Quadratic_program_solution<CGAL::MP_Float> Solution;

int main()
{
  std::vector<Point_d> points;
  // convex hull: 4-gon spanned by {(1,0), (4,1), (4,4), (2,3)}
  points.push_back (Point_d (1, 0)); // point 0
  points.push_back (Point_d (4, 1)); // point 1
  points.push_back (Point_d (4, 4)); // point 2
  points.push_back (Point_d (2, 3)); // point 3
 
  // test all 25 integer points in [0,4]^2
  for (int i=0; i<=4; ++i)
    for (int j=0; j<=4; ++j) {
      Point_d p (i, j);
      Solution s = solve_convex_hull_containment_lp
	(p, points.begin(), points.end(), CGAL::MP_Float());
      std::cout << p;
      if (s.is_infeasible())
	std::cout << " is not in the convex hull\n";
      else {
	assert (s.is_optimal());
	std::cout << " is a convex combination of the points ";
	Solution::Index_iterator it = s.basic_variable_indices_begin();
	Solution::Index_iterator end = s.basic_variable_indices_end();
	for (; it != end; ++it) std::cout << *it << " ";
	std::cout << std::endl;
      }
    }
  return 0;
}

It turns out that exactly three of the four points contribute to any convex combination, even through there are lattice points that lie in the convex hull of less than three of the points. This shows that the set of basic variables that we access in the example does not necessarily coincide with the set of important variables as defined above. In fact, it is only guaranteed that a non-basic variable attains one of its bounds, but there might be basic variables that also have this property. In linear and quadratic programming terms, such a situation is called a degeneracy.

There is also the concept of an important constraint: this is typically a constraint in the system $$Ax ~ b that is satisfied with equality at $$x^*. Program QP_solver/first_qp_basic_constraints.cpp shows how these can be accessed, using the iterators basic_constraint_indices_begin() and basic_constraint_indices_end().

Again, we have a disagreement between ``basic'' and ``important'': it is guaranteed that all basic constraints are satisfied with equality at $$x^*, but there might be non-basic constraints that are satisfied with equality as well.

61.7   Solution Certificates

Certificates are proofs that the solver can give you in order to convince you that what it claims is indeed true. The archetype of such a proof is Farkas Lemma [MG06].

Farkas Lemma: Either the inequality system

A x		b
x		0

has a solution $$x^*, or there exists a vector $$y such that

y		0
yTA		0
yTb	<	0,

but not both.

Thus, if someone wants to convince you that the first system in the Farkas Lemma is infeasible, that person can simply give you a vector $$y that solves the second system. Since you can easily verify yourself that the $$y you got satisfies this second system, you now have a certificate for the infeasibility of the first system, assuming that you believe in Farkas Lemma.

Here we show how the solver can convince you. We first set up an infeasible linear program with constraints of the type $$Ax b, x 0; then we solve it and ask for a certificate. Finally, we verify the certificate by simply checking the inequalities of the second system in Farkas Lemma.

File: examples/QP_solver/infeasibility_certificate.cpp

#include <cassert>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

// program and solution types
typedef CGAL::Nonnegative_linear_program_from_iterators
<int**,                                                // for A
 int*,                                                 // for b
 CGAL::Comparison_result*,                             // for r
 int*>                                                 // for c 
Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;

// we demonstrate Farkas Lemma: either the system 
//     A x <= b
//       x >= 0
// has a solution, or there exists y such that
//       y >= 0 
//    y^TA >= 0 
//    y^Tb <  0
// In the following instance, the first system has no solution,
// since adding up the two inequalities gives x_2 <= -1:
//     x_1 - 2x_2  <=  1
//    -x_1 + 3x_2  <= -2
//     x_1,   x_2  >=  0

int main() {
  int  Ax1[] = { 1, -1};                        // column for x1
  int  Ax2[] = {-2,  3};                        // column for x2
  int*   A[] = {Ax1, Ax2};                      // A comes columnwise
  int    b[] = {1, -2};                         // right-hand side
  CGAL::Comparison_result 
    r[] = {CGAL::SMALLER, CGAL::SMALLER};      // constraints are "<="
  int    c[] = {0, 0};                         // zero objective function

  // now construct the linear program; the first two parameters are
  // the number of variables and the number of constraints (rows of A)
  Program lp (2, 2, A, b, r, c);

  // solve the program, using ET as the exact type
  Solution s = CGAL::solve_nonnegative_linear_program(lp, ET());

  // get certificate for infeasibility
  assert (s.is_infeasible());
  Solution::Infeasibility_certificate_iterator y = 
    s.infeasibility_certificate_begin();
  // check y >= 0
  assert (y[0] >= 0);
  assert (y[1] >= 0);
  // check y^T A >= 0
  assert (y[0] * A[0][0] + y[1] * A[0][1] >= 0);
  assert (y[0] * A[1][0] + y[1] * A[1][1] >= 0);
  // check y^T b < 0
  assert (y[0] * b[0] + y[1] * b[1] < 0);

  return 0;
}

There are similar certificates for optimality and unboundedness that you can see in action in the programs QP_solver/optimality_certificate.cpp and QP_solver/unboundedness_certificate.cpp. The underlying variants of Farkas Lemma are somewhat more complicated, due to the mixed relations in $$ ~  and the general bounds. The certificate section of Quadratic_program_solution<ET> gives the full picture and mathematically proves the correctness of the certificates.

61.8   Customizing the Solver

61.8.1   Exponent Overflow in Double Using Floating-Point Filters

Hint: If you have a program where the number of variables $$n and the number of constraints $$m have the same order of magnitude, the filtering will usually have no dramatic effect on the performance, so in that case you might as well switch to QP_PARTIAL_DANTZIG to be safe from the issue described here (see QP_solver/cycling.cpp for an example that shows how to change the pricing strategy).

61.8.2   The Solver Internally Cycles

File: examples/QP_solver/cycling.cpp

#include <iostream>
#include <fstream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

// program and solution types
typedef CGAL::Quadratic_program_from_mps<double> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;

int main() {
  std::ifstream in ("cycling.mps");
  Program lp(in);         // read program from file
  assert (lp.is_valid()); // we should have a valid mps file...
  assert (lp.is_linear());      // ... and it should be linear...
  assert (lp.is_nonnegative()); // as well as nonnegative

  // solve the program, using ET as the exact type
  // choose verbose mode and Bland pricing
  CGAL::Quadratic_program_options options;
  options.set_verbosity(1);                         // verbose mode 
  options.set_pricing_strategy(CGAL::QP_BLAND);     // Bland's rule
  options.set_auto_validation(true);                // automatic self-check
  Solution s = CGAL::solve_nonnegative_linear_program(lp, ET(), options);
  assert (s.is_valid());                     // did the self-check succeed?

  // output solution
  std::cout << s;
  return 0;
}

If you comment the line

options.set_pricing_strategy(CGAL::QP_BLAND);          // Bland's rule

In general, the verbose mode can be of use when you are not sure whether the solver ``has died'', or whether it simply takes very long to solve your problem. We refer to the class Quadratic_program_options for further details.

61.9   Some Benchmarks

Still, the example shows that the performance can be dramatically affected by switching between pricing strategies, and we give some hints on how to achieve good performance in general.

The application is the one already discussed in Section 61.5 above: testing whether a point is in the convex hull of other points. To be able to switch between pricing strategies, we add another parameter of type Quadratic_program_options to the function solve_convex_hull_containment_lp that we pass on to the solution function:

File: examples/QP_solver/solve_convex_hull_containment_lp3.h

#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_options.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>

// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin  {
  typedef typename Point_d::Homogeneous_const_iterator result_type;
  result_type operator() (const Point_d& p) const {
    return p.homogeneous_begin();
  }
};

// function to test whether point is in the convex hull of other points;
// the type ET is an exact type used for the computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
				  RandomAccessIterator begin,
				  RandomAccessIterator end, const ET& dummy,
				  const CGAL::Quadratic_program_options& o)
{
  // construct program and solve it
  return CGAL::solve_nonnegative_linear_program
    (CGAL::make_nonnegative_linear_program_from_iterators
     (end-begin,                                                           // n
      p.dimension()+1,                                                     // m
      boost::transform_iterator
      <Homogeneous_begin<Point_d>, RandomAccessIterator>(begin),           // A
      typename Point_d::Homogeneous_const_iterator (p.homogeneous_begin()),// b
      CGAL::Const_oneset_iterator<CGAL::Comparison_result>(CGAL::EQUAL),   // ~
      CGAL::Const_oneset_iterator
      <typename CGAL::Kernel_traits<Point_d>::Kernel::RT> (0)),            // c
      dummy, o);   
}

Now let us test containment of the origin in the convex hull of $$n random points in $$[0,1]^d (it will most likely not be contained, and it turns out that this is the most expensive case). In the program below, we use $$d=10 and $$n=100,000, and we comment on some other combinations of $$n and $$d below (feel free to experiment with still other values).

File: examples/QP_solver/convex_hull_containment_benchmarks.cpp

#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Random.h>
#include <CGAL/Timer.h>
#include "solve_convex_hull_containment_lp3.h"

// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif

typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;

int main()
{
  const int d = 10;       // change this in order to experiment
  const int n = 100000;   // change this in order to experiment

  // generate n random d-dimensional points in [0,1]^d
  CGAL::Random rd;
  std::vector<Point_d> points;
  for (int j =0; j<n; ++j) {
    std::vector<double> coords;
    for (int i=0; i<d; ++i) 
      coords.push_back(rd.get_double());
    points.push_back (Point_d (d, coords.begin(), coords.end()));
  }
  
  // benchmark all pricing strategies in turn
  CGAL::Quadratic_program_pricing_strategy strategy[] = {
    CGAL::QP_CHOOSE_DEFAULT,              // QP_PARTIAL_FILTERED_DANTZIG
    CGAL::QP_DANTZIG,                     // Dantzig's pivot rule...
    CGAL::QP_PARTIAL_DANTZIG,             // ... with partial pricing
    CGAL::QP_BLAND,                       // Bland's pivot rule
    CGAL::QP_FILTERED_DANTZIG,            // Dantzig's filtered pivot rule...
    CGAL::QP_PARTIAL_FILTERED_DANTZIG     // ... with partial pricing
  };
  
  CGAL::Timer t;
  for (int i=0; i<6; ++i) {
    // test strategy i
    CGAL::Quadratic_program_options options;
    options.set_pricing_strategy (strategy[i]);
    t.reset(); t.start();
    // is origin in convex hull of the points? (most likely, not)
    solve_convex_hull_containment_lp 
      (Point_d (d, CGAL::ORIGIN), points.begin(), points.end(), 
       ET(0), options);
    t.stop();
    std::cout << "Time (s) = " << t.time() << std::endl;
  }

  return 0;
}

If you compile with the macros NDEBUG or CGAL_QP_NO_ASSERTIONS set (this is essential for good performance!!), you will see runtimes that qualitatively look as follows (on your machine, the actual runtimes will roughly be some fixed multiples of the numbers in the table below, and they might vary with the random choices). The default choice of the pricing strategy in that case is QP_PARTIAL_FILTERED_DANTZIG.

We clearly see the effect of filtering: we gain a factor of ten, roughly, compared to the next best non-filtered variant.

61.9.1   $$d=3, $$n=1,000,000

In general, if your problem has a high variable/constraint or constraint/variable ratio, then filtering will typically pay off. In such cases, it might be beneficial to encode your problem using input type double in order to profit from the filtering (but see the issue discussed in Section 61.8.1).

61.9.2   $$d=100, $$n=100,000

61.9.3   $$d=500, $$n=1,000

In general, if you have a program where the number of variables and the number of constraints have the same order of magnitude, then the saving gained from using the filtered approach is typically small. In such a situation, you should consider switching to a non-filtered variant in order to avoid the rare issue discussed in Section 61.8.1 altogether.