Chapter 22
2D Snap Rounding

Table of Contents

22.1   Introduction

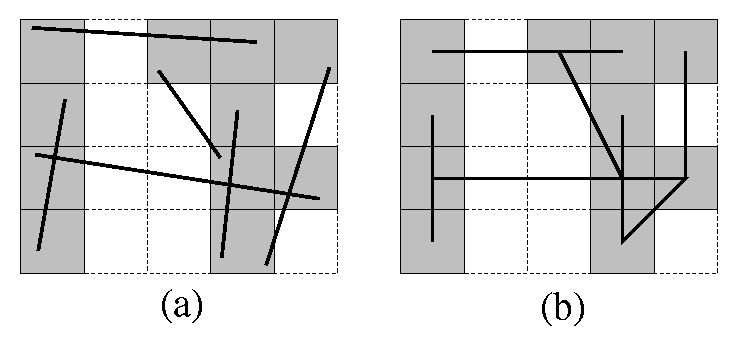
Figure 22.1:  An arrangement of segments before (a) and after (b) SR (hot pixels are shaded)

22.2   What is Snap Rounding/Iterated Snap Rounding

()

In a snap-rounded arrangement, the distance between a vertex and a non-incident edge can be extremely small compared with the width of a pixel in the grid used for rounding. ISR is a modification of SR which makes a vertex and a non-incident edge well separated (the distance between each is at least half-the-width-of-a-pixel). However, the guaranteed quality of the approximation in ISR degrades. Figure 22.2 depicts the results of SR and ISR on the same input. Conceptually, the ISR procedure is equivalent to repeated application of SR, namely we apply SR to the original set of segments, then we use the output of SR as input to another round of SR and so on until all the vertices are well separated from non-incident edges. Algorithmically we operate differently, as this repeated application of SR would have resulted in an efficient overall process. The algorithmic details are given in [HP02].

22.3   Terms and Software Design

Our package supports both schemes, implementing the algorithm described in [HP02]. Although the paper only describes an algorithm for ISR, it is easy to derive an algorithm for SR, by performing only the first rounding level for each segment.

The input to the program is a set $$S of $$n segments, $$S={s₁,...,s_n} and the output is a set $$G of $$n polylines, with a polyline $$g_i for each input segments $$s_i. An input segment is given by the coordinates of its endpoints. An output polyline is given by the ordered set of vertices $$v₀,...,v_k along the polyline. The polyline consists of the segments $$(v₀v₁),...,(v_k-1v_k).

There are three template parameters: Traits is the underlying geometry, i.e., the number type used and the coordinate representation. InputIterator is the type of the iterators that point to the first and after-the-last elements of the input. Finally, OutputContainer is the type of the output container.

Since the algorithm requires kernel functionalities such as the rounding to the center of a pixel, a special traits class must be provided. The precise description of the requirements is given by the concept SnapRoundingTraits_2. The class Snap_rounding_traits_2 is a model of this concept.

Figure 22.2:  An arrangement of segments before (a), after SR (b) and ISR (c) (hot pixels are shaded).

22.4   Four Line Segment Example

The following example generates an ISR representation of an arrangement of four line segments. In particular it produces a list of points that are the vertices of the resulting polylines in a plane tiled with one-unit square pixels.

File: examples/Snap_rounding_2/snap_rounding.cpp

#include <CGAL/basic.h>
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Snap_rounding_traits_2.h>
#include <CGAL/Snap_rounding_2.h>

typedef CGAL::Quotient<CGAL::MP_Float>           Number_type;
typedef CGAL::Cartesian<Number_type>             Kernel;
typedef CGAL::Snap_rounding_traits_2<Kernel>     Traits;
typedef Kernel::Segment_2                        Segment_2;
typedef Kernel::Point_2                          Point_2;
typedef std::list<Segment_2>                     Segment_list_2;
typedef std::list<Point_2>                       Polyline_2;
typedef std::list<Polyline_2>                    Polyline_list_2;

int main()
{
  Segment_list_2 seg_list;
  Polyline_list_2 output_list;

  seg_list.push_back(Segment_2(Point_2(0, 0), Point_2(10, 10)));
  seg_list.push_back(Segment_2(Point_2(0, 10), Point_2(10, 0)));
  seg_list.push_back(Segment_2(Point_2(3, 0), Point_2(3, 10)));
  seg_list.push_back(Segment_2(Point_2(7, 0), Point_2(7, 10)));

  // Generate an iterated snap-rounding representation, where the centers of
  // the hot pixels bear their original coordinates, using 5 kd trees:
  CGAL::snap_rounding_2<Traits,Segment_list_2::const_iterator,Polyline_list_2>
    (seg_list.begin(), seg_list.end(), output_list, 1.0, true, false, 5);

  int counter = 0;
  Polyline_list_2::const_iterator iter1;
  for (iter1 = output_list.begin(); iter1 != output_list.end(); ++iter1) {
    std::cout << "Polyline number " << ++counter << ":\n";
    Polyline_2::const_iterator iter2;
    for (iter2 = iter1->begin(); iter2 != iter1->end(); ++iter2)
      std::cout << "    (" << iter2->x() << ":" << iter2->y() << ")\n";
  }

  return(0);
}

This program generates four polylines, one for each input segment. The exact output follows:

Polyline number 1:
    (0/4:0/4)
    (12/4:12/4)
    (20/4:20/4)
    (28/4:28/4)
    (40/4:40/4)
Polyline number 2:
    (0/4:40/4)
    (12/4:28/4)
    (20/4:20/4)
    (28/4:12/4)
    (40/4:0/4)
Polyline number 3:
    (12/4:0/4)
    (12/4:12/4)
    (12/4:28/4)
    (12/4:40/4)
Polyline number 4:
    (28/4:0/4)
    (28/4:12/4)
    (28/4:28/4)
    (28/4:40/4)

The package is supplied with a graphical demo program that opens a window, allows the user to edit segments dynamically, applies a selected snap-rounding procedures, and displays the result onto the same window (see <CGAL_ROOT>/demo/Snap_rounding_2/demo.cpp).