
 |
A subdivision method recursively refines a coarse mesh and generates an ever closer approximation to a smooth surface. Subdivision_method_3 consists of four subdivision methods and their refinement hosts. Each refinement host is a template function of a polyhedron class and a geometry policy class. It refines the connectivity of the control mesh and computes the geometry of the refined mesh. The geometry computation is dedicated to the custom geometry policy. A geometry policy consists of functions that compute the new point based on the subdivision stencil. A stencil defines the footprint (a submesh of the control mesh) of a new point.
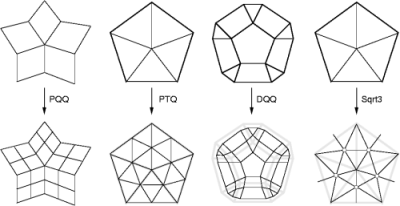
The four supported refinement hosts are the primal quadrilateral quadrisection (PQQ), the primal triangle quadrisection (PTQ), the dual quadrilateral quadrisection (DQQ), and the triangulation. These refinements are respectively used in Catmull-Clark, Loop, Doo-Sabin and subdivision.
#include <CGAL/Subdivision_method_3.h>
|
| ||
|
|
| |
| applies the PQQ refinement on the control mesh p step times. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. | ||
|
| ||
|
|
| |
| applies the PTQ refinement on the control mesh p step times, where p contains only triangle facets. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined. | ||
|
| ||
|
|
| |
| applies the DQQ refinement on the control mesh p step times. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. | ||
|
| ||
|
|
| |
| applies the triangulation on the control mesh p step times, where p contains only triangle facets. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined. | ||
|
| ||
|
|
| |
| applies Catmull-Clark subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies Loop subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies Doo-Sabin subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
CGAL::CatmullClark_mask_3<Polyhedron_3>
CGAL::Loop_mask_3<Polyhedron_3>
CGAL::Sqrt3_mask_3<Polyhedron_3>
This example program subdivides a polyhedral mesh with Catmull-Clark subdivision.
File: examples/Subdivision_method_3/CatmullClark_subdivision.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Subdivision_method_3.h>
#include <iostream>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
typedef CGAL::Cartesian<double> Kernel;
typedef CGAL::Polyhedron_3<Kernel> Polyhedron;
using namespace std;
using namespace CGAL;
int main(int argc, char** argv) {
if (argc != 2) {
cout << "Usage: CatmullClark_subdivision d < filename" << endl;
cout << " d: the depth of the subdivision (0 < d < 10)" << endl;
cout << " filename: the input mesh (.off)" << endl;
return 0;
}
int d = argv[1][0] - '0';
Polyhedron P;
cin >> P; // read the .off
Subdivision_method_3::CatmullClark_subdivision(P,d);
cout << P; // write the .off
return 0;
}