
 |
The concept TriangulationDataStructure_2 describes the requirements for the second template parameter of the basic triangulation class Triangulation_2<Traits,Tds> and of all other 2D triangulation classes.
The concept can be seen as a container for the faces and vertices of the triangulation. The concept TriangulationDataStructure_2 includes two sub-concepts TriangulationDataStructure_2::Vertex and TriangulationDataStructure_2::Face.
The TriangulationDataStructure_2 maintains incidence and adjacency relations among vertices and faces.
Each triangular face gives access to its three incident vertices and to its three adjacent faces. Each vertex gives access to one of its incident faces and through that face to the circular list of its incident faces.
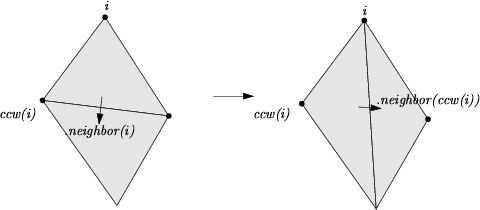
The three vertices of a face are indexed with 0, 1 and 2. The neighbors of a face are also indexed with 0,1,2 in such a way that the neighbor indexed by i is opposite to the vertex with the same index.
Each edge has two implicit representations : the edge of a face f which is opposed to the vertex indexed i, can be represented as well as an edge of the neighbor(i) of f. See Figure 25.2
The triangulation data structure is responsible for the combinatorial integrity of the triangulation. This means that the triangulation data structure allows to perform some combinatorial operations on the triangulation and guarantees the maintenance on proper incidence and adjacency relations among the vertices and faces. The term combinatorial operations means that those operations are purely topological and do not depend on the geometric embedding. Insertion of a new vertex in a given face, or in a given edge, suppression of a vertex of degree three, flip of two edges are examples of combinatorial operations.
|
| |
|
Size type (unsigned integral type)
| |
|
| |
|
Difference type (signed integral type)
| |
|
| |
|
The vertex type. Requirements for this type
are described in concept TriangulationDataStructure_2::Vertex
.
| |
|
| |
|
The face type. Requirements for this type
are described in concept TriangulationDataStructure_2::Face
.
| |
Vertices and faces are accessed via Vertex_handle and Face_handle. These types are models of the concept Handles which basically supports the two dereference operators * and ->.
|
| |
|
Handle to a vertex
| |
|
| |
|
Handle to a face.
| |
|
| ||
|
| The edge type. The Edge(f,i) is edge common to faces f and f.neighbor(i). It is also the edge joining the vertices vertex(cw(i)) and vertex(ccw(i)) of f. | |
The following iterators allow one to visit all the vertices, edges and faces of a triangulation data structure. They are all bidirectional, non-mutable iterators.
|
| |
|
| |
|
|
The following circulators allow to visit all the edges or faces incident to a given vertex and all the vertices adjacent to a given vertex. They are all bidirectional and non mutable.
|
| |
|
| |
|
|
Iterators and circulators are convertible to the corresponding handles, thus they can be passed directly as argument to the functions expecting a handle.
|
| |
|
default constructor.
| |
|
| |
|
Copy constructor. All the vertices and faces are duplicated.
| |
|
|
| Assignation. All the vertices and faces of tds1 are duplicated in tds . Former faces and vertices of tds , if any, are deleted | ||
|
|
| |||
tds1 is copied into tds. If , the vertex of tds
corresponding to v is returned, otherwise Vertex_handle()
is returned.
| ||||
|
|
| Swaps tds and tds1. Should be preferred to tds=tds1 or tds(tds1) when tds1 is deleted after that. | ||
|
|
| Deletes all faces and all finite vertices. | ||
|
|
| returns the dimension of the triangulation. |
|
|
| returns the number of vertices in the data structure. |
|
|
| returns the number of two dimensional faces in the data structure. |
|
|
| returns the number of edges in the triangulation data structure. |
|
|
| returns the number of full dimensional faces, i.e. faces of dimension equal to the dimension of the triangulation. This is the actual number of faces stored in the triangulation data structure. |
|
|
| returns true if v is a vertex of tds. |
|
|
| |
| tests whether (fh,i) is an edge of tds. Answers false when dimension() . | ||
|
|
| |
| returns true if va vb is an edge of tds. | ||
|
|
| |
| as previous. In addition, if true is returned fr and i are set such that the pair (fr,i) is the description of the ordered edge va vb. | ||
|
|
| tests whether fh is a face of tds. Answers false when dimension() . |
|
|
| |
| true if there is a face having v1, v2 andv3 as vertices. | ||
|
|
| |
| as above. In addition, if true is returned, fr is a pointer to the face with v1, v2 and v3 as vertices. | ||
Three circulator classes allow to traverse the edges or faces incident to a vertex or the vertices adjacent to this vertex.. A face circulator is invalidated by any modification of the face it points to. An edge circulator is invalidated by any modification of anyone of the two faces incident to the edge pointed to. A vertex circulator that turns around vertex v and that has as value a pointer to vertex w, is invalidated by any modification of anyone of the two faces incident to v and w.
|
|
| |||
| ||||
|
|
| |||
| ||||
|
|
| |||
| ||||
|
|
| |||
| returns vertex of f->neighbor(i). | ||||
|
|
| |||
| returns the index of f as a neighbor of f->neighbor(i). | ||||
|
|
| exchanges the edge incident to f and f->neighbor(i) with the other diagonal of the quadrilateral formed by f and f->neighbor(i). |
|
|
| creates the first vertex and returns a pointer to it. |
|
|
| creates the second vertex and returns a pointer to it. |
|
|
| |
| adds a vertex v splitting edge i of face f. Return a pointer to v. | ||
|
|
| |
| adds a vertex v splitting face f in three. Face f is modified, two new faces are created. Return a pointer to v | ||
|
|
| |
| adds a vertex v, increasing by one the dimension of the triangulation. Vertex v and the existing vertex w are linked to all the vertices of the triangulation. The Boolean orient decides the final orientation of all faces. A pointer to vertex v is returned. | ||
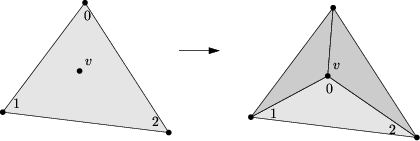
|
|
| |||
removes a vertex of degree 3. Two of the incident faces are destroyed,
the third one is modified.
If parameter f is specified, it has to be a face incident to v
and will be the modified face.
| ||||
|
|
| |||
| removes the before last vertex. | ||||
|
|
| |||
| removes the last vertex. | ||||
|
|
| |||
removes vertex v incident to all other vertices
and decreases by one the dimension of the triangulation.
| ||||

| advanced |

|
|
| ||||
|
|
| |||
| creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end[. Returns a pointer to the vertex. | ||||
|
| ||||
|
|
| |||
| same as above, except that, to build the new faces, the algorithm first recycles faces in the sequence [face_begin, face_end[ and create new ones when the sequence is exhausted. | ||||
|
| ||||
|
|
| |||
| uses vertex v to star the hole whose boundary is described by the sequence of edges[edge_begin, edge_end[. | ||||
|
| ||||
|
|
| |||
| same as above, recycling faces in the sequence [face_begin, face_end[ . | ||||
|
|
| |||
| removes the vertex v, and store in hole the list of edges on the boundary of the hole. | ||||
|
|
| adds a new vertex. | ||
|
|
| |||
| adds a face which is the neighbor i1 of f1, i2 of f2 and i3 of f3. | ||||
|
|
| |||
| adds a face which is the neighbor i1 of f1, and the neighbor i2 of f2. | ||||
|
|
| |||
| adds a face which is the neighbor i1 of f1, and has v as vertex. | ||||
|
|
| |||
| adds a face with vertices v1, v2 and v3. | ||||
|
|
| |||
| adds a face with vertices v1, v2 and v3, and neighbors f1, f2, f3. | ||||
|
|
| adds a face whose vertices and neighbors are set to NULL. | ||
|
|
| deletes a face. | ||
|
|
| |||
| deletes a vertex. | ||||

| advanced |

|
|
|
|
returns modulo 3.
| ||
|
|
|
returns modulo 3.
| ||
|
|
| checks the combinatorial validity of the triangulation: call the is_valid() member function for each vertex and each face, checks the number of vertices and the Euler relation between numbers of vertices, faces and edges. | ||
|
|
| Returns the degree of v in the triangulation. |
The information output in the iostream is: the dimension, the number of (finite) vertices, the number of (finite) faces. Then comes for each vertex, the non combinatorial information stored in that vertex if any. Then comes for each faces, the indices of its vertices and the non combinatorial information (if any) stored in this face. Then comes for each face again the indices of the neighboring faces. The index of an item (vertex of face) the rank of this item in the output order. When dimension 2, the same information is output for faces of maximal dimension instead of faces.
|
|
| |
| writes tds into the stream os. If v is not a null handle, vertex v is output first or skipped if skip_first is true. | ||
|
|
| |
| inputs tds from file and returns a pointer to the first input vertex. If skip_first is true, it is assumed that the first vertex has been omitted when output. | ||
|
|
| |
| reads a combinatorial triangulation from is and assigns it to tds | ||
|
|
| |
| writes tds into the stream os | ||