Chapter 28
3D Triangulation Data Structure

Table of Contents

A geometric triangulation has two aspects: the combinatorial structure, which gives the incidence and adjacency relations between faces, and the geometric information related to the position of vertices.

CGAL provides 3D geometric triangulations in which these two aspects are clearly separated. As described in Chapter 27, a geometric triangulation of a set of points in $$ ^d, $$d 3 is a partition of the whole space $$ ^d into cells having $$d+1 vertices. Some of them are infinite, they are obtained by linking an additional vertex at infinity to each facet of the convex hull of the points (see Section 27.1). The underlying combinatorial graph of such a triangulation without boundary of $$ ^d can be seen as a triangulation of the topological sphere $$S^d in $$ ^d+1.

This chapter deals with 3D-triangulation data structures, meant to maintain the combinatorial information for 3D-geometric triangulations. The reader interested in geometric triangulations of $$ ³ is advised to read Chapter 27.

28.1   Representation

In CGAL, a 3D triangulation data structure is a container of cells ($$3-faces) and vertices ($$0-faces). Each cell gives access to its four incident vertices and to its four adjacent cells. Each vertex gives direct access to one of its incident cells, which is sufficient to retrieve all the incident cells when needed.

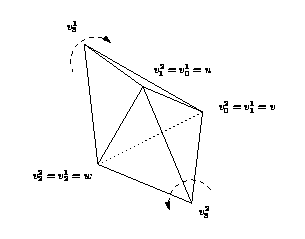
The four vertices of a cell are indexed with 0, 1, 2 and 3. The neighbors of a cell are also indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by $$i is opposite to the vertex with the same index (see Figure 28.1).

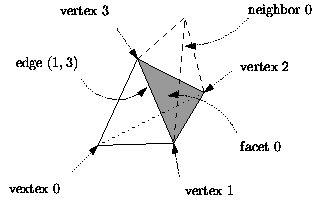
Edges ($$1-faces) and facets ($$2-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex of index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of indices i and j of c).

Degenerate Dimensions As CGAL explicitly deals with all degenerate cases, a 3D-triangulation data structure in CGAL can handle the cases when the dimension of the triangulation is lower than 3.

Thus, a 3D-triangulation data structure can store a triangulation of a topological sphere $$S^d of $$ ^d+1, for any $$d {-1,0,1,2,3}.

Let us give, for each dimension, the example corresponding to the triangulation data structure having a minimal number of vertices, i.e. a simplex. These examples are illustrated by presenting their usual geometric embedding.

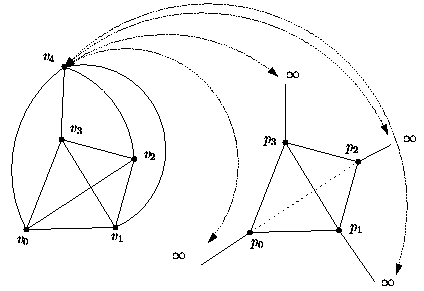
• dimension 3. The triangulation data structure consists of the boundary of a 4-dimensional simplex, which has 5 vertices. A geometric embedding consists in choosing one of these vertices to be infinite, thus four of the five 3-cells become infinite: the geometric triangulation has one finite tetrahedron remaining, each of its facets being incident to an infinite cell. See Figure 28.2. Figure 28.2:  4D simplex and a 3D geometric embedding.
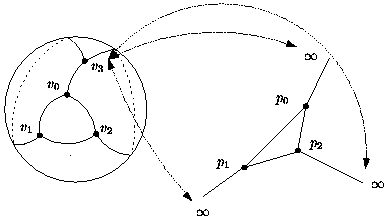
• dimension 2. We have 4 vertices forming one 3-dimensional simplex, i.e. the boundary of a tetrahedron. The geometric embedding in the plane results from choosing one of these vertices to be infinite, then the geometric triangulation has one finite triangle whose edges are incident to the infinite triangles. See Figure 28.3. Figure 28.3:  3D simplex and a 2D geometric embedding.
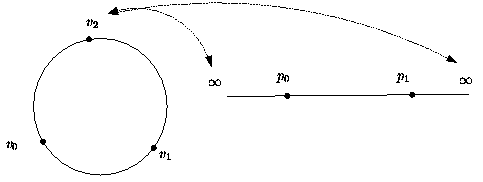
• dimension 1. A 2-dimensional simplex (a triangle) has 3 vertices. The geometric embedding is an edge whose vertices are linked to an infinite point. See Figure 28.4. Figure 28.4:  2D simplex and a 1D geometric embedding.

The last three cases are defined uniquely:

• dimension 0. A 0-dimensional triangulation is combinatorially equivalent to the boundary of a 1-dimensional simplex (an edge), which consists of 2 vertices. One of them becomes infinite in the geometric embedding, and there is only one finite vertex remaining. The two vertices are adjacent.
• dimension -1. This dimension is a convention to represent a 0-dimensional simplex, that is a sole vertex, which will be geometrically embedded as an ``empty'' triangulation, having only one infinite vertex.
• dimension -2. This is also a convention. The triangulation data structure has no vertex. There is no associated geometric triangulation.

Note that the notion of infinite vertex has no meaning for the triangulation data structure. The infinite vertex of the geometric embedding is a vertex that cannot be distinguished from the other vertices in the combinatorial triangulation.

The same cell class is used in all cases: triangular faces in 2D can be considered as degenerate cells, having only three vertices (resp. neighbors) numbered $$(0,1,2); edges in 1D have only two vertices (resp. neighbors) numbered $$0 and $$1.

The implicit representation of facets (resp. edges) still holds for degenerate ($$< 3) dimensions : in dimension 2, each cell has only one facet of index 3, and 3 edges $$(0,1), $$(1,2) and $$(2,0); in dimension 1, each cell has one edge $$(0,1).

Validity A 3D combinatorial triangulation is said to be locally valid iff the following is true:

(a) When a cell $$c has a neighbor pointer to another cell $$c', then reciprocally this cell $$c' has a neighbor pointer to $$c, and $$c and $$c' have three vertices in common. These cells are called adjacent.

(b) The cells have a coherent orientation: if two cells $$c₁ and $$c₂ are adjacent and share a facet with vertices $$u,v,w, then the vertices of $$c₁ are numbered $$(v₀¹ = u, v₁¹ = v, v₂¹ = w, v₃¹), and the vertices of $$c₂ are numbered $$(v₀² = v, v₁² = u, v₂² = w, v₃²), up to positive permutations of $$(0,1,2,3). In other words, if we embed the triangulation in $$ ³, then the fourth vertices $$v₃¹ and $$v₃² of $$c₁ and $$c₂ see the common facet in opposite orientations. See Figure 28.5.

The set $$$$₄ of permutations of $$(0,1,2,3) has cardinality 24, and the set of positive permutations $$A₄ has cardinality 12. Thus, for a given orientation, there are up to 12 different orderings of the four vertices of a cell. Note that cyclic permutations are negative and so do not preserve the orientation of a cell.

The is_valid() method provided by Triangulation_data_structure_3 checks the local validity of a given triangulation data structure.

28.2   Software Design

The 3D-triangulation data structure class of CGAL, Triangulation_data_structure_3, is designed to be used as a combinatorial layer upon which a geometric layer can be built [Ket98]. This geometric layer is typically one of the 3D-triangulation classes of CGAL: Triangulation_3, Delaunay_triangulation_3 and Regular_triangulation_3. This relation is described in more details in Chapter 27, where the Section 27.5 explains other important parts of the design related to the geometry.

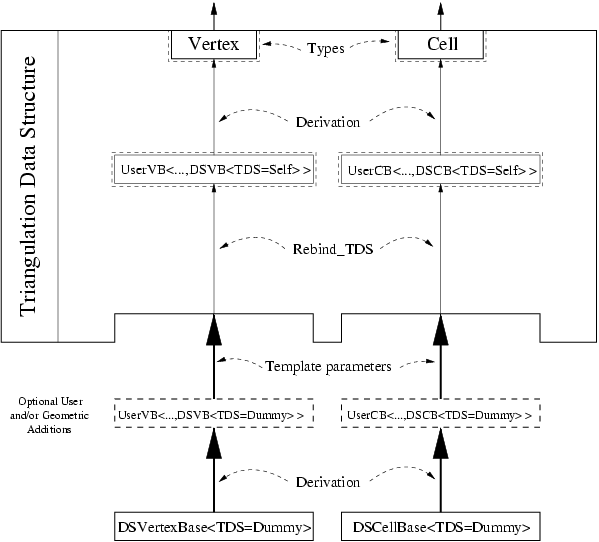
We focus here on the design of the triangulation data structure (TDS) itself, which the Figure 28.6 illustrates.

28.2.1   Flexibility of the Design

In order for the user to be able to add his own data in the vertices and cells, the design of the TDS is split into two layers:

• In the bottom layer, the (vertex and cell) base classes store elementary incidence and adjacency (and possibly geometric or other) information. These classes are parameterized by the TDS which provides the handle types. (They can also be parameterized by a geometric traits class or anything else.) A vertex stores a Cell_handle, and a cell stores four Vertex_handles and four Cell_handles.

• The middle layer is the TDS, which is purely combinatorial. It provides operations such as insertion of a new vertex in a given cell, on a $$1 or $$2-face. It also allows one, if the dimension of the triangulation is smaller than $$3, to insert a vertex so that the dimension of the triangulation is increased by one. The TDS is responsible for the combinatorial integrity of the eventual geometric triangulation built on top of it (the upper layer, see Chapter 27).

The user has several ways to add his own data in the vertex and cell base classes used by the TDS. He can either:

• use the classes Triangulation_vertex_base_with_info and Triangulation_cell_base_with_info, which allow to add one data member of a user provided type, and give access to it.
• derive his own classes from the default base classes Triangulation_ds_vertex_base, and Triangulation_ds_cell_base (or the geometric versions typically used by the geometric layer, Triangulation_vertex_base, and Triangulation_cell_base).
• write his own base classes following the requirements given by the concepts TriangulationCellBase_3 and TriangulationVertexBase_3 .

28.2.2   Cyclic Dependency

Since adjacency relations are stored in the vertices and cells, it means that the vertex and cell base classes have to be able to store handles (an entity akin to pointers) to their neighbors in the TDS. This in turns means that the vertex and cell base classes have to know the types of these handles, which are provided by the TDS. So in a sense, the base classes are parameterized by the TDS, and the TDS is parameterized by the vertex and cell base classes ! This is a cycle which cannot be resolved easily.

The solution that we have chosen is similar to the mechanism used by the standard class std::allocator: the vertex and cell base classes are initially given a fake or dummy TDS template parameter, whose unique purpose is to provide the types that can be used by the vertex and cell base classes (such as handles). Then, inside the TDS itself, these base classes are rebound to the real TDS type, that is we obtain the same vertex and cell base classes, but parameterized with the real TDS instead of the dummy one. Rebinding is performed by a nested template class of the vertex and cell base classes (see code below), which provides a type which is the rebound vertex or cell base class¹.

Here is how it works, schematically:

template < class Vb, class Cb >
class TDS
{
  typedef TDS<Vb, Cb>    Self;

  // Rebind the vertex and cell base to the actual TDS (Self).
  typedef typename Vb::template Rebind_TDS<Self>::Other  VertexBase;
  typedef typename Cb::template Rebind_TDS<Self>::Other  CellBase;

  // ... further internal machinery leads to the final public types:
public:
  typedef ...  Vertex;
  typedef ...  Cell;
  typedef ...  Vertex_handle;
  typedef ...  Cell_handle;
};

template < class TDS = ... >  // The default is some internal type faking a TDS
class Triangulation_ds_vertex_base_3
{
public:
  template < class TDS2 >
  struct Rebind_TDS {
    typedef Triangulation_ds_vertex_base_3<TDS2>    Other;
  };
...
};

When derivation is used for the vertex or cell base classes, which is the case at the geometric level with Triangulation_vertex_base_3, then it gets slightly more involved because its base class has to be rebound as well:

template < class GT, class Vb = Triangulation_ds_vertex_base_3<> >
class Triangulation_vertex_base_3 : public Vb
{
public:
  template < class TDS2 >
  struct Rebind_TDS {
    typedef typename Vb::template Rebind_TDS<TDS2>::Other  Vb2;
    typedef Triangulation_vertex_base_3<GT, Vb2>           Other;
  };
...
};

28.2.3   Backward Compatibility

28.3   Examples

28.3.1   Incremental Construction

File: examples/Triangulation_3/tds.cpp

#include <CGAL/Triangulation_data_structure_3.h>
#include <iostream>
#include <fstream>
#include <cassert>
#include <vector>

typedef CGAL::Triangulation_data_structure_3<>      Tds;

typedef Tds::size_type                              size_type;
typedef Tds::Cell_handle                            Cell_handle;
typedef Tds::Vertex_handle                          Vertex_handle;

int main()
{
  Tds T;

  assert( T.number_of_vertices() == 0 );
  assert( T.dimension() == -2 );
  assert( T.is_valid() );

  std::vector<Vertex_handle> PV(7);

  PV[0] = T.insert_increase_dimension();
  assert( T.number_of_vertices() == 1 );
  assert( T.dimension() == -1 );
  assert( T.is_valid() );

  // each of the following insertions of vertices increases the dimension
  for ( int i=1; i<5; i++ ) {
    PV[i] = T.insert_increase_dimension(PV[0]);
    assert( T.number_of_vertices() == (size_type) i+1 );
    assert( T.dimension() == i-1 );
    assert( T.is_valid() );
  }
  assert( T.number_of_cells() == 5 );

  // we now have a simplex in dimension 4

  // cell incident to PV[0]
  Cell_handle c = PV[0]->cell();
  int ind;
  bool check = c->has_vertex( PV[0], ind );
  assert( check );
  // PV[0] is the vertex of index ind in c

  // insertion of a new vertex in the facet opposite to PV[0]
  PV[5] = T.insert_in_facet(c, ind);

  assert( T.number_of_vertices() == 6 );
  assert( T.dimension() == 3 );
  assert( T.is_valid() );

  // insertion of a new vertex in c
  PV[6] = T.insert_in_cell(c);

  assert( T.number_of_vertices() == 7 );
  assert( T.dimension() == 3 );
  assert( T.is_valid() );

  std::ofstream oFileT("output_tds",std::ios::out);
  // writing file output_tds;
  oFileT << T;

  return 0;
}

28.3.2   Cross-Linking Between a 2D and a 3D Data Structures

File: examples/Triangulation_3/linking_2d_and_3d.cpp

#include <CGAL/Triangulation_data_structure_2.h>
#include <CGAL/Triangulation_data_structure_3.h>
#include <cassert>

// declare the 2D vertex base type, parametrized by some 3D TDS.
template < typename T3, typename Vb = CGAL::Triangulation_ds_vertex_base_2<> >
class My_vertex_2;

// declare the 3D vertex base type, parametrized by some 2D TDS.
template < typename T2, typename Vb = CGAL::Triangulation_ds_vertex_base_3<> >
class My_vertex_3;

// Then, we have to break the dependency cycle.

// we need to refer to a dummy 3D TDS.
typedef CGAL::Triangulation_ds_vertex_base_3<>::Triangulation_data_structure
        Dummy_tds_3;
// the 2D TDS, initially plugging a dummy 3D TDS in the vertex type
// (to break the dependency cycle).
typedef CGAL::Triangulation_data_structure_2<My_vertex_2<Dummy_tds_3> >  TDS_2;
// the 3D TDS, here we can plug the 2D TDS directly.
typedef CGAL::Triangulation_data_structure_3<My_vertex_3<TDS_2> >        TDS_3;


template < typename T3, typename Vb >
class My_vertex_2
  : public Vb
{
public:
  typedef typename Vb::Face_handle    Face_handle;

  template <typename TDS2>
  struct Rebind_TDS {
    typedef typename Vb::template Rebind_TDS<TDS2>::Other  Vb2;
    // we also have to break the cycle here by hardcoding TDS_3 instead of T3.
    typedef My_vertex_2<TDS_3, Vb2>                        Other;
  };

  My_vertex_2() {}

  My_vertex_2(Face_handle f) : Vb(f) {}

  // we store a vertex handle of the 3D TDS.
  typename T3::Vertex_handle v3;
};

template < typename T2, typename Vb >
class My_vertex_3
  : public Vb
{
public:
  typedef typename Vb::Cell_handle    Cell_handle;

  template <typename TDS2>
  struct Rebind_TDS {
    typedef typename Vb::template Rebind_TDS<TDS2>::Other  Vb2;
    typedef My_vertex_3<T2, Vb2>                           Other;
  };

  My_vertex_3() {}

  My_vertex_3(Cell_handle c) : Vb(c) {}

  // we store a vertex handle of the 2D TDS.
  typename T2::Vertex_handle v2;
};


int main() {
  TDS_2 t2;
  TDS_3 t3;

  TDS_2::Vertex_handle v2 = t2.insert_dim_up();
  TDS_3::Vertex_handle v3 = t3.insert_increase_dimension();

  v2->v3 = v3;
  v3->v2 = v2;

  assert(t2.is_valid());
  assert(t3.is_valid());
  return 0;
}

28.4   Design and Implementation History

Monique Teillaud introduced the triangulation of the topological sphere $$S^d in $$ ^d+1 to manage the underlying graph of geometric triangulations and handle degenerate dimensions [Tei99].

Sylvain Pion improved the software in several ways, in particular regarding the memory management.

Footnotes