Chapter 29
2D Triangulations

Table of Contents

This chapter describes the two dimensional triangulations of CGAL. Section 29.1 recalls the main definitions about triangulations. Sections 29.2 discusses the way two-dimensional triangulations are represented in CGAL . Section 29.3 presents the overall software design of the 2D triangulations package. The next sections present the different two dimensional triangulations classes available in CGAL: basic triangulations (section 29.4), Delaunay triangulations (Section 29.5), regular triangulations (Section 29.6), constrained triangulations (Section 29.7), and constrained Delaunay triangulations (Section 29.8). Section 29.9 describes a class which implements a constrained or constrained Delaunay triangulation with an additional data structure to describe how the constraints are refined by the edges of the triangulations. Section 29.10 describes a hierarchical data structure for fast point location queries. At last, Section 29.11 explains how the user can benefit from the flexibility of CGAL triangulations using customized classes for faces and vertices.

29.1   Definitions

A two dimensional triangulation can be roughly described as a set $$T of triangular facets such that :
- two facets either are disjoint or share a lower dimensional face (edge or vertex).
- the set of facets in $$T is connected for the adjacency relation.
- the domain $$U_T which is the union of facets in $$T has no singularity.

More precisely, a triangulation can be described as a simplicial complex. Let us first record a few definitions.

A simplicial complex is a set $$T of simplices such that 
- any face of a simplex in $$T is a simplex in $$T
- two simplices in $$T either are disjoint or share a common sub-face.

The dimension $$d of a simplicial complex is the maximal dimension of its simplices.
A simplicial complex $$T is pure if any simplex of $$T is included in a simplex of $$T with maximal dimension.
Two simplexes in $$T with maximal dimension $$d are said to be adjacent if they share a $$(d-1) dimensional sub-face. A simplicial complex is connected if the adjacency relation defines a connected graph over the set of simplices of $$T with maximal dimension.
The union $$U_T of all simplices in $$T is called the domain of $$T. A point $$p in the domain of $$T is said to singular if its surrounding in $$U_T is neither a topological ball nor a topological disc.

Then, a two dimensional triangulation can be described as a two dimensional simplicial complex that is pure, connected and without singularity.

Each facet of a triangulation can be given an orientation which in turn induces an orientation on the edges incident to that facet. The orientation of two adjacent facets are said to be consistent if they induce opposite orientations on their common incident edge. A triangulation is said to be orientable if the orientation of each facet can be chosen in such a way that all pairs of incident facets have consistent orientations.

The data structure underlying CGAL triangulations allows to represent the combinatorics of any orientable two dimensional triangulations without boundaries. On top of this data structure, the 2D triangulations classes take care of the geometric embedding of the triangulation and are designed to handle planar triangulations. The plane of the triangulation may be embedded in a higher dimensional space.

The triangulations of CGAL are complete triangulations which means that their domain is the convex hull of their vertices. Because any planar triangulation can be completed, this is not a real restriction. For instance, a triangulation of a polygonal region can be constructed and represented as a subset of a constrained triangulation in which the region boundary edges have been input as constrained edges (see Section 29.7, 29.8 and 29.9).

Strictly speaking, the term face should be used to design a face of any dimension, and the two-dimensional faces of a triangulation should be properly called facets. However, following a common usage, we hereafter often call faces, the facets of a two dimensional triangulation.

29.2   Representation

The set of faces

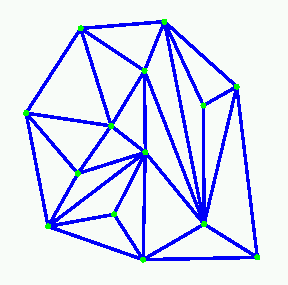
A 2D triangulation of CGAL can be viewed as a planar partition whose bounded faces are triangular and cover the convex hull of the set of vertices. The single unbounded face of this partition is the complementary of the convex hull. In many applications, such as Kirkpatrick's hierarchy or incremental Delaunay construction, it is convenient to deal with only triangular faces. Therefore, a fictitious vertex, called the infinite vertex is added to the triangulation as well as infinite edges and infinite faces incident to it.. Each infinite edge is incident to the infinite vertex and to a vertex of the convex hull. Each infinite face is incident to the infinite vertex and to a convex hull edge.

Therefore, each edge of the triangulation is incident to exactly two faces and the set of faces of a triangulation is topologically equivalent to a two-dimensional sphere. This extends to lower dimensional triangulations arising in degenerate cases or when the triangulations as less than three vertices. Including the infinite faces, a one dimensional triangulation is a ring of edges and vertices topologically equivalent to a $$1-sphere. A zero dimensional triangulation, whose domain is reduced to a single point, is represented by two vertices that is topologically equivalent to a $$0-sphere.

Note that the infinite vertex has no significant coordinates and that no geometric predicate can be applied on it nor on an infinite face.

Figure 29.1:  Infinite vertex and infinite faces

A representation based on faces and vertices

The basic elements of the representation are vertices and faces. Each triangular face gives access to its three incident vertices and to its three adjacent faces. Each vertex gives access to one of its incident faces and through that face to the circular list of its incident faces.

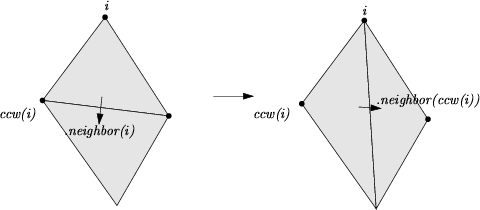
The three vertices of a face are indexed with 0, 1 and 2 in counterclockwise order. The neighbors of a face are also indexed with 0,1,2 in such a way that the neighbor indexed by i is opposite to the vertex with the same index. See Figure 29.2, the functions ccw(i) and cw(i) shown on this figure compute respectively $$i+1 and $$i-1 modulo 3.

The edges are not explicitly represented, they are only implicitly represented through the adjacency relations of two faces. Each edge has two implicit representations: the edge of a face f which is opposed to the vertex indexed i, can be represented as well as an edge of the neighbor(i) of f.

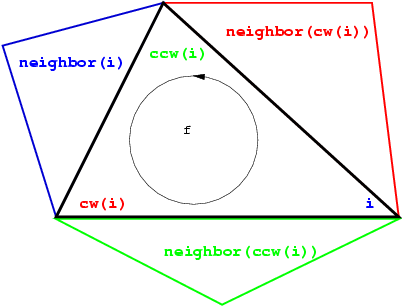
Figure 29.2:  Vertices and neighbors.

29.3   Software Design

The triangulations classes of CGAL provide high-level geometric functionalities such as location of a point in the triangulation, insertion or removal of a point. They are build as a layer on top of a data structure called the triangulation data structure. The triangulation data structure can be thought of as a container for the faces and vertices of the triangulation. This data structure also takes care of all the combinatorial aspects of the triangulation.

This separation between the geometric aspect and the combinatorial part is reflected in the software design by the fact that the triangulation classes have two template parameters:

• the first parameter stands for a geometric traits class providing the geometric primitives (points, segments and triangles) of the triangulation and the elementary operations (predicate or constructions) on those objects.

• the second parameter stands for a triangulation data structure class. The concept of triangulation data structure is described in Section 30.2 of Chapter 30. The triangulation data structure defines the types used to represent the faces and vertices of the triangulation, as well as additional types (handles, iterators and circulators) to access and visit the faces and vertices.

  CGAL provides the class Triangulation_data_structure_2<Vb,Fb> as a default model of triangulation data structure. The class Triangulation_data_structure_2<Vb,Fb> has two template parameters standing for a vertex class and a face class. CGAL defines concepts for these template parameters and provide default models for these concepts. The vertex and base classes are templated by the geometric traits which allows them to have some knowledge of the geometric primitives of the triangulation. Those default vertex and face base classes can be replaced by user customized base classes in order, for example, to deal with additional properties attached to the vertices or faces of a triangulation. See section 29.11 for more details on the way to make use of this flexibility.

The Figure 29.3 summarizes the design of the triangulation package, showing the three layers (base classes, triangulation data structure and triangulation) forming this design.

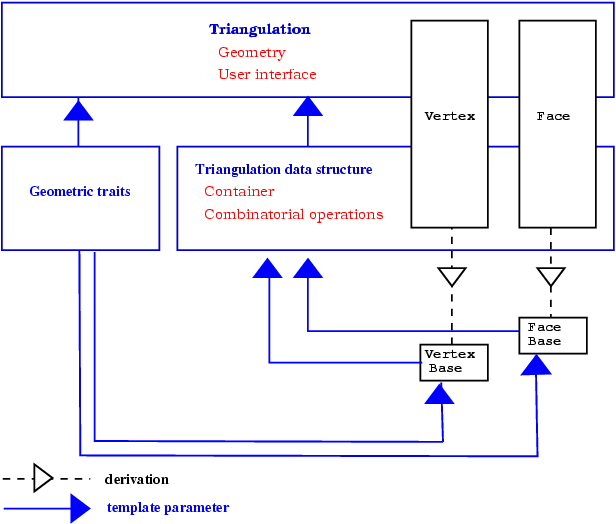
Figure 29.3:  The triangulations software design.

The top triangulation level, responsible for the geometric embedding of the triangulation comes in different flavors according to the different kind of triangulations: basic, Delaunay, regular, constrained or constrained Delaunay. Each kind of triangulations correspond to a different class. Figure 29.4 summarizes the derivation dependencies of CGAL 2D triangulations classes. Any 2D triangulation class is parametrized by a geometric traits and a triangulation data structure. While a unique concept TriangulationDataStructure_2 describes the triangulation data structure requirements for any triangulation class, the concept of geometric traits actually depends on the triangulation class. In general, the requirements for the vertex and face base classes are described by the basic concepts TriangulationVertexBase_2 and TriangulationFaceBase_2. However, some triangulation classes requires base classes implementing refinements of the basic concepts.

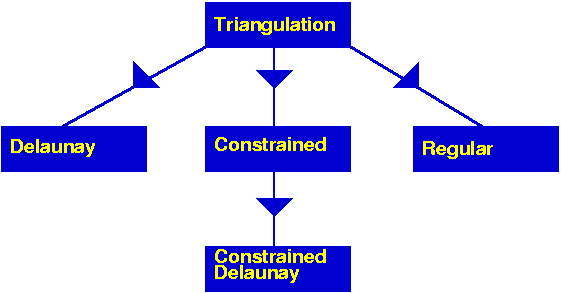
Figure 29.4:  The derivation tree of 2D triangulations.

29.4   Basic Triangulations

29.4.1   Description

The class Triangulation_2<Traits,Tds> serves as a base class for the other 2D triangulations classes and implements the user interface to a triangulation.

The vertices and faces of the triangulations are accessed through handles, iterators and circulators. A handle is a model of the concept Handle which basically offers the two dereference operators * and -> . A circulator is a type devoted to visit circular sequences. Handles are used whenever the accessed element is not part of a sequence. Iterators and circulators are used to visit all or parts of the triangulation.

The iterators and circulators are all bidirectional and non mutable. The circulators and iterators are convertible to the handles with the same value type, so that when calling a member function, any handle type argument can be replaced by an iterator or a circulator with the same value type.

The triangulation class allows to visit the vertices and neighbors of a face in clockwise or counterclockwise order.

There are circulators to visit the edges or faces incident to a given vertex or the vertices adjacent to it. Another circulator type allows to visit all the faces traversed by a given line. Circulators step through infinite features as well as through finite ones.

The triangulation class offers some iterators to visit all the faces, edges or vertices and also iterators to visit selectively the finite faces, edges or vertices.

The triangulation class provides methods to test the infinite character of any feature, and also methods to test the presence in the triangulation of a particular feature (edge or face) given its vertices.

The triangulation class provides a method to locate a given point with respect to a triangulation. In particular, this method reports whether the point coincides with a vertex of the triangulation, lies on an edge, in a face or outside of the convex hull. In case of a degenerate lower dimensional triangulation, the query point may also lie outside the triangulation affine hull.

The triangulation class also provides methods to locate a point with respect to a given finite face of the triangulation or with respect to its circumcircle. The faces of the triangulation and their circumcircles have the counterclockwise orientation.

The triangulation can be modified by several functions : insertion of a point, removal of a vertex, flipping of an edge. The flipping of an edge is possible when the union of the two incident faces forms a convex quadrilateral (see Figure 29.5).

Figure 29.5:  Flip.

Figure 29.6:  Flip.

Implementation

Locate is implemented by a line walk. The walk begins at a vertex of the face which is given as an optional argument or at an arbitrary vertex of the triangulation if no optional argument is given. It takes time O(n) in the worst case, but only O(sqrt(n)) on average if the vertices are distributed uniformly at random. The class Triangulation_hierarchy_2<Traits,Tds>, described in section 29.10, implements a data structure designed to offer an alternate more efficient point location algorithm.

Insertion of a point is done by locating a face that contains the point, and splitting this face into three new faces. If the point falls outside the convex hull, the triangulation is restored by flips. Apart from the location, insertion takes a time O(1). This bound is only an amortized bound for points located outside the convex hull.

Removal of a vertex is done by removing all adjacent triangles, and re-triangulating the hole. Removal takes a time at most proportional to d^2, where d is the degree of the removed vertex, which is O(1) for a random vertex.

The face, edge, and vertex iterators on finite features are derived from their counterparts visiting all (finite and infinite) features which are themselves derived from the corresponding iterators of the triangulation data structure.

Geometric Traits

The geometric traits of a triangulation is required to provide the geometric objects (points, segments and triangles) building up the triangulation together with the geometric predicates on those objects. The required predicates are:
- comparison of the x or y coordinates of two points.
- the orientation test which computes the order type of three given point.

The concept TriangulationTraits_2 describes the requirements for the geometric traits class of a triangulation. The CGAL kernel classes are models for this concept. The CGAL library also provides dedicated models of TriangulationTraits_2 using the kernel geometric objects and predicates. These classes are themselves templated with a CGAL kernel and extract the required types and predicates from the kernel. The traits class Triangulation_euclidean_traits_2<R> is designed to deal with ordinary two dimensional points. The class Triangulation_euclidean_traits_xy_3<R> is a geometric traits class to build the triangulation of a terrain. Such a triangulation is a two-dimensional triangulation embedded in three dimensional space. The data points are three-dimensional points. The triangulation is build according to the projections of those points on the $$xy plane and then lifted up to the original three-dimensional data points. This is especially useful to deal with GIS terrains. Instead of really projecting the three-dimensional points and maintaining a mapping between each point and its projection (which costs space and is error prone), the traits class supplies geometric predicates that ignore the z-coordinates of the points. See Section 29.5 for an example. CGAL provides also the geometric traits classes Triangulation_euclidean_traits_yz_3<R> and Triangulation_euclidean_traits_zx_3<R> to deal with projections on the xz plane and yz-plane, respectively.

29.4.2   Example of a Basic Triangulation

The following program creates a triangulation of 2D points using the default kernel Exact_predicate_inexact_constructions_kernel as geometric traits and the default triangulation data structure. The input points are read from a file and inserted in the triangulation. Finally points on the convex hull are written to cout.

File: examples/Triangulation_2/triangulation_prog1.cpp

#include <fstream>

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Triangulation_2.h>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};

typedef CGAL::Triangulation_2<K>         Triangulation;
typedef Triangulation::Vertex_circulator Vertex_circulator;
typedef Triangulation::Point             Point;

int main() {
  std::ifstream in("data/triangulation_prog1.cin");
  std::istream_iterator<Point> begin(in);
  std::istream_iterator<Point> end;

  Triangulation t;
  t.insert(begin, end);

  Vertex_circulator vc = t.incident_vertices(t.infinite_vertex()),
    done(vc);
  if (vc != 0) {
    do { std::cout << vc->point() << std::endl;
    }while(++vc != done);
  }
  return 0;
}

29.5   Delaunay Triangulations

29.5.1   Description

The class Delaunay_triangulation_2<Traits,Tds> derives from the class Triangulation_2<Traits,Tds>.

The class Delaunay_triangulation_2<Traits,Tds> inherits the types defined by the basic class Triangulation_2<Traits,Tds>. Additional types, provided by the traits class, are defined to represent the dual Voronoi diagram.

The class Delaunay_triangulation_2<Traits,Tds> overwrites the member functions that insert a new point in the triangulation or remove a vertex from it to maintain the Delaunay property. It also has a member function (Vertex_handle nearest_vertex(const Point& p)) to answer nearest neighbor queries and member functions to construct the elements (vertices and edges) of the dual Voronoi diagram.

Geometric traits

L

L

The CGAL kernel classes and the class Triangulation_euclidean_traits_2<R> are models of the concept DelaunayTriangulationTraits_2 for the euclidean metric. The traits class for terrains, Triangulation_euclidean_traits_xy_3<R>,
Triangulation_euclidean_traits_yz_3<R>, and
Triangulation_euclidean_traits_zx_3<R>
are also models of DelaunayTriangulationTraits_2 except that they do not fulfill the requirements for the duality functions and nearest vertex queries.

Implementation

Removal calls the removal in the triangulation and then re-triangulates the hole created in such a way that the Delaunay criterion is satisfied. Removal of a vertex of degree d takes time O(d^2). The degree $$d is O(1) for a random vertex in the triangulation.

After having performed a point location, the nearest neighbor of a point is found in time O(n) in the worst case, but in time O(1) for vertices distributed uniformly at random and any query point.

29.5.2   Example: a Delaunay Terrain

The following code creates a Delaunay triangulation with the usual Euclidean metric for the vertical projection of a terrain model. The points have elevation, that is they are 3D points, but the predicates used to build the Delaunay triangulation are computed using only the $$x and $$y coordinates of these points.

File: examples/Triangulation_2/terrain.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Triangulation_euclidean_traits_xy_3.h>
#include <CGAL/Delaunay_triangulation_2.h>

#include <fstream>


typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_euclidean_traits_xy_3<K>  Gt;
typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;

typedef K::Point_3   Point;

int main()
{
  std::ifstream in("data/terrain.cin");
  std::istream_iterator<Point> begin(in);
  std::istream_iterator<Point> end;

  Delaunay dt;
  dt.insert(begin, end);
  std::cout << dt.number_of_vertices() << std::endl;
  return 0;
}

29.5.3   Example: Voronoi Diagram

File: examples/Triangulation_2/voronoi.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>

#include <fstream>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Delaunay_triangulation_2<K>  Triangulation;
typedef Triangulation::Edge_iterator  Edge_iterator;
typedef Triangulation::Point          Point;

int main( )
{
  std::ifstream in("data/voronoi.cin");
  std::istream_iterator<Point> begin(in);
  std::istream_iterator<Point> end;
  Triangulation T;
  T.insert(begin, end);

  int ns = 0;
  int nr = 0;
  Edge_iterator eit =T.edges_begin();
  for ( ; eit !=T.edges_end(); ++eit) {
    CGAL::Object o = T.dual(eit);
    if (CGAL::object_cast<K::Segment_2>(&o)) {++ns;}
    else if (CGAL::object_cast<K::Ray_2>(&o)) {++nr;}
  }
  std::cout << "The Voronoi diagram has " << ns << " finite edges "
	    << " and " << nr << " rays" << std::endl;
  return 0;
}

29.6   Regular Triangulations

29.6.1   Description

The power diagram of the set $$ PW is a space partition in which each cell corresponds to a sphere $$(p_i, w_i) of $$ PW and is the locus of points $$p whose power with respect to $$(p_i, w_i) is less than its power with respect to any other sphere in $$ PW. In the two-dimensional space, the dual of this diagram is a triangulation whose domain covers the convex hull of the set $$ P= { p_i, i = 1, ..., n } of center points and whose vertices form a subset of $$ P. Such a triangulation is called a regular triangulation. Three points $$p_i, p_j and $$p_k of $$ P form a triangle in the regular triangulation of $$ PW iff there is a point $$p of the plane with equal powers with respect to $$(p_i, w_i), $$(p_j, w_j) and $$(p_k, w_k) and such that this power is less than the power of $$p with respect to any other sphere in $$ PW.

Let us defined the power product of two weighted points $$(p_i, w_i) and $$(p_j, w_j) as:

$$(p_i, w_i,p_j, w_j) = p_ip_j ² - w_i - w_j .

$$(p_i, w_i,p_j, 0) is simply the power of point $$p_j with respect to the sphere $$(p_i, w_i), and two weighted points are said to be orthogonal if their power product is null. The power circle of three weighted points $$(p_i, w_i), $$(p_j, w_j) and $$(p_k, w_k) is defined as the unique circle $$(, ) orthogonal to $$(p_i, w_i), $$(p_j, w_j) and $$(p_k, w_k).

The regular triangulation of the sets $$ PW satisfies the following regular property (which just reduces to the Delaunay property when all the weights are null): a triangle $$p_ip_jp_k is a face of the regular triangulation of $$ PW iff the power product of any weighted point $$(p_l, w_l) of $$ PW with the power circle of $$(p_i, w_i), $$(p_j, w_j) and $$(p_k, w_k) is positive or null. We call power test of $$(p_i, w_i), $$(p_j, w_j), $$(p_k, w_k), and $$(p_l, w_l), the predicates which amount to compute the sign of the power product of $$(p_l, w_l) with respect to the power circle of $$(p_i, w_i), $$(p_j, w_j) and $$(p_k, w_k). This predicate amounts to computing the sign of the following determinant

$$|

A pair of neighboring faces $$p_ip_jp_k and $$p_ip_jp_l is said to be locally regular (with respect to the weights in $$ PW) if the power test of $$(p_i, w_i), $$(p_j, w_j), $$(p_k, w_k), and $$(p_l, w_l) is positive. A classical result of computational geometry establishes that a triangulation of the convex hull of $$ P such that any pair of neighboring faces is regular with respect to $$ PW, is a regular triangulation of $$ PW.

Alternatively, the regular triangulation of the weighted points set $$ PW can be obtained as the projection on the two dimensional plane of the convex hull of the set of three dimensional points $$ P'= { (p_i,p_i ² - w_i ), i = 1, ..., n }.

The class Regular_triangulation_2<Traits, Tds> is designed to maintain the regular triangulation of a set of $$2d weighted points. It derives from the class Triangulation_2<Traits, Tds>. The functions insert and remove are overwritten to handle weighted points and maintain the regular property. The vertices of the regular triangulation of a set of weighted points $$PW correspond only to a subset of $$PW. Some of the input weighted points have no cell in the dual power diagrams and therefore do not correspond to a vertex of the regular triangulation. Such a point is called a hidden point. Because hidden points can reappear later on as vertices when some other point is removed, they have to be stored somewhere. The regular triangulation store those points in special vertices, called hidden vertices. A hidden point can reappear as vertex of the triangulation only when the two dimensional face that hides it is removed from the triangulation. To deal with this feature, each face of a regular triangulation stores a list of hidden vertices. The points in those vertices are reinserted in the triangulation when the face is removed.

Regular triangulation have member functions to construct the vertices and edges of the dual power diagrams.

The geometric traits

Note that, since the type Weighted_point is not defined in CGAL kernels, plugging a filtered kernel such as Exact_predicates_exact_constructions_kernel in Regular_triangulation_euclidean_traits_2<K,Weight> will in fact not provide exact predicates on weighted points. To solve this, there is also another model of the traits concept, Regular_triangulation_filtered_traits_2<FK>, which is providing filtered predicates (exact and efficient). The argument FK must be a model of the Kernel concept, and it is also restricted to be a instance of the Filtered_kernel template.

The Vertex type and Face Type of a Regular Triangulation

The base vertex type of a regular triangulation includes a Boolean data member to mark the hidden state of the vertex. Therefore CGAL defines the concept RegularTriangulationVertexBase_2 which refine the concept TriangulationVertexBase_2 and provides a default model for this concept.

The base face type of a regular triangulation is required to provide a list of hidden vertices, designed to store the points hidden by the face. It has to be a model of the concept RegularTriangulationFaceBase_2. CGAL provides the templated class Regular_triangulation_face_base_2<Traits> as a default base class for faces of regular triangulations.

29.6.2   Example: a Regular Triangulation

The following code creates a regular triangulation of a set of weighted points and output the number of vertices and the number of hidden vertices.

File: examples/Triangulation_2/regular.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Regular_triangulation_euclidean_traits_2.h>
#include <CGAL/Regular_triangulation_filtered_traits_2.h>
#include <CGAL/Regular_triangulation_2.h>

#include <fstream>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Regular_triangulation_filtered_traits_2<K>  Traits;
typedef CGAL::Regular_triangulation_2<Traits> Regular_triangulation;

int main()
{
   Regular_triangulation rt;
   std::ifstream in("data/regular.cin");

   Regular_triangulation::Weighted_point wp;
   int count = 0;
   while(in >> wp){
       count++;
     rt.insert(wp);
   }
   rt.is_valid();
   std::cout << "number of inserted points : " << count << std::endl;
   std::cout << "number of vertices :  " ;
   std::cout << rt.number_of_vertices() << std::endl;
   std::cout << "number of hidden vertices :  " ;
   std::cout << rt.number_of_hidden_vertices() << std::endl;
   return 0;
}

29.7   Constrained Triangulations

A constrained triangulation is a triangulation of a set of points that has to include among its edges a given set of segments joining the points. The corresponding edges are called constrained edges.

The endpoints of constrained edges are of course vertices of the triangulation. However the triangulation may include include other vertices as well. There are three versions of constrained triangulations.

• In the basic version, the constrained triangulation does not handle intersecting constraints, and the set of input constraints is required to be a set of segments that do not intersect except possibly at their endpoints. Any number of constrained edges are allowed to share the same endpoint. Vertical constrained edges or constrained edges with null length are allowed.
• The two other versions support intersecting input constraints. In those versions, input constraints are allowed to be intersecting, overlapping or partially overlapping segments. The triangulation introduces additional vertices at each point that is the proper intersection points of two constraints. A single constraint intersecting other constraints will then appear as several edges in the triangulation. The two versions dealing with intersecting constraints differ in the way intersecting constraints are dealt with.
  • One of them is designed to be robust when predicates are evaluated exactly but constructions (i. e. intersection computations) are approximate.
  • The other one is designed to be used with exact arithmetic (meaning exact evaluation of predicates and exact computation of intersections.) This last version finds its full efficiency when used in conjunction with a constraint hierarchy data structure (which allows one to avoid the cascading of intersection computations) as provided in the class Constrained_triangulation_plus_2. See section 29.9.

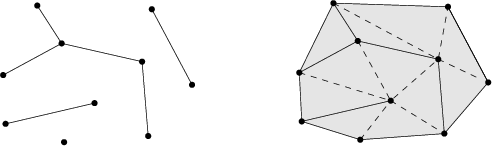
A constrained triangulation is represented in the CGAL library as an object of the class Constrained_triangulation_2<Traits,Tds,Itag>. The third parameter Itag is the intersection tag which serves to choose how intersecting constraints are dealt with. This parameter has to be instantiated by one of the following classes : CGAL::No_intersection_tag when input constraints do not intersect
CGAL::Exact_predicates_tag if the geometric traits provides exact predicates but approximate constructions
CGAL::Exact_intersections_tag when an exact predicates and exact constructions are provided.

The class Constrained_triangulation_2<Traits,Tds, Itag> inherits from Triangulation_2<Traits,Tds>. It defines an additional type Constraint to represent the constraints. A constraint is represented as a pair of points.

A constrained triangulation can be created from a list of constrained edges. The class Constrained_triangulation_2<Traits,Tds,Itag> overrides the insertion and removal of a point to take care of the information about constrained edges. The class also allows inline insertion of a new constraint, given by its two endpoints or the removal of a constraint.

The Geometric Traits

The Base Face of a Constrained Triangulation

CGAL provides a default base face class for constrained triangulations. This class, named Constrained_triangulation_face_base_2<Traits>, derives from the class Triangulation_face_base_2<Traits> and adds three Boolean data members to store the status of its edges.

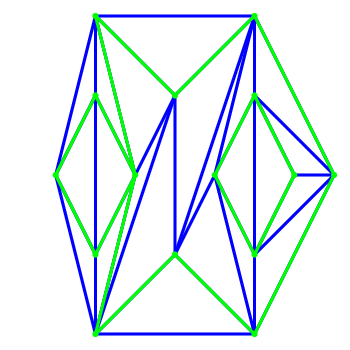
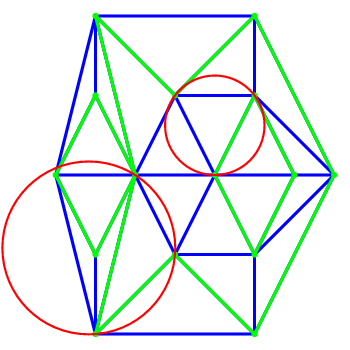
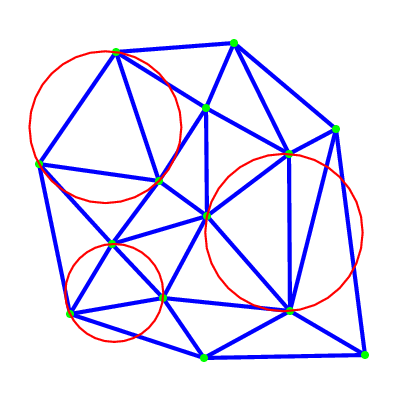
Figure 29.7:  Constrained and Constrained Delaunay triangulation: the constraining edges are the green edges, a constrained triangulation is shown on the left, the constrained Delaunay triangulation with two examples of circumcircles is shown on the right.

29.8   Constrained Delaunay Triangulations

A constrained Delaunay triangulation is a triangulation with constrained edges which tries to be as much Delaunay as possible. As constrained edges are not necessarily Delaunay edges, the triangles of a constrained Delaunay triangulation do not necessarily fulfill the empty circle property but they fulfill a weaker constrained empty circle property. To state this property, it is convenient to think of constrained edges as blocking the view. Then, a triangulation is constrained Delaunay iff the circumscribing circle of any facet encloses no vertex visible from the interior of the facet. As in the case of constrained triangulations, three different versions of Delaunay constrained triangulations are provided. The first version handle set of constraints which do not intersect except possibly at the endpoints. The two other versions handle intersecting input constraints. One of them is designed to be designed to be robust when used in conjunction with a geometric traits providing exact predicates and approximate constructions (such as a CGAL::Filtered_Kernel or any kernel providing filtered exact predicates). The third version is designed to be used with an exact arithmetic number type.

The CGAL class Constrained_Delaunay_triangulation_2<Traits,Tds,Itag> is designed to represent constrained Delaunay triangulations.

As in the case of constraints triangulation, the third parameter Itag is the intersection tag and serves to choose how intersecting constraints are dealt with. It can be instantiated with one of the following class : CGAL::No_intersection_tag, CGAL::Exact_predicates_tag, CGAL::Exact_intersections_tag (see Section 29.7.

A constrained Delaunay triangulation is not a Delaunay triangulation but it is a constrained triangulation. Therefore the class Constrained_Delaunay_triangulation_2<Traits,Tds,Itag> derives from the class Constrained_triangulation_2<Traits,Tds,Itag>.

The constrained Delaunay triangulation has member functions to override the insertion and removal of a point or of a constraint. Each of those member function takes care to restore the constrained empty circle property.

The Geometric Traits

The face base class

29.8.1   Example: a Constrained Delaunay Triangulation

File: examples/Triangulation_2/constrained.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Constrained_Delaunay_triangulation_2.h>

#include <cassert>
#include <iostream>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Triangulation_vertex_base_2<K>                     Vb;
typedef CGAL::Constrained_triangulation_face_base_2<K>           Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb>              TDS;
typedef CGAL::Exact_predicates_tag                               Itag;
typedef CGAL::Constrained_Delaunay_triangulation_2<K, TDS, Itag> CDT;
typedef CDT::Point          Point;

int
main( )
{
  CDT cdt;
  std::cout << "Inserting a grid of 5x5 constraints " << std::endl;
  for (int i = 1; i < 6; ++i)
    cdt.insert_constraint( Point(0,i), Point(6,i));
  for (int j = 1; j < 6; ++j)
    cdt.insert_constraint( Point(j,0), Point(j,6));

  assert(cdt.is_valid());
  int count = 0;
  for (CDT::Finite_edges_iterator eit = cdt.finite_edges_begin();
       eit != cdt.finite_edges_end();
       ++eit)
    if (cdt.is_constrained(*eit)) ++count;
  std::cout << "The number of resulting constrained edges is  ";
  std::cout <<  count << std::endl;
  return 0;
}

29.9   Constrained Triangulations Plus

The class Constrained_triangulation_plus_2<Tr> provides a constrained triangulation with an additional data structure called the constraint hierarchy that keeps track of the input constraints and of their refinement in the triangulation. The class Constrained_triangulation_plus_2<Tr> inherits from its template parameter Tr, which has to be instantiated by a constrained or constrained Delaunay triangulation. According to its intersection tag, the base class will support intersecting input constraints or not. When intersections of input constraints are supported, the base class constructs a triangulation of the arrangement of the constraints, introducing new vertices at each proper intersection points and refining the input constraints into sub-constraints which appear as edges (more precisely as constrained edges) of the triangulation. The data structure maintains for each input constraint the sequence of intersection vertices added on this constraint. The constraint hierarchy also allows the user to retrieve the set of constrained edges of the triangulation, and for each constrained edge, the set of input constraints that overlap it.

The class Constrained_triangulation_plus_2<Tr> is especially useful when the base constrained triangulation class handles intersections of constraints and uses an exact number type, i.e. when its intersection tag is CGAL::Exact_intersections_tag. Indeed in this case, the Constrained_triangulation_plus_2<Tr> is specially designed to avoid cascading in the computations of intersection points.

29.9.1   Example: Building a Triangulated Arrangement of Segments

The following code inserts a set of intersecting constraint segments into a triangulation and counts the number of constrained edges of the resulting triangulation.

File: examples/Triangulation_2/constrained_plus.cpp

#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/intersections.h>
#include <CGAL/Constrained_Delaunay_triangulation_2.h>
#include <CGAL/Constrained_triangulation_plus_2.h>

#include <cassert>
#include <iostream>

typedef CGAL::Exact_predicates_exact_constructions_kernel K;

typedef CGAL::Triangulation_vertex_base_2<K>              Vb;
typedef CGAL::Constrained_triangulation_face_base_2<K>    Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb>       TDS;
typedef CGAL::Exact_intersections_tag                     Itag;
typedef CGAL::Constrained_Delaunay_triangulation_2<K,TDS,Itag> CDT;
typedef CGAL::Constrained_triangulation_plus_2<CDT>       CDTplus;
typedef CDTplus::Point                                    Point;

int
main( )
{
  CDTplus cdt;
  std::cout  << "Inserting a grid 5 x 5 of constraints " << std::endl;
  for (int i = 1; i < 6; ++i)
    cdt.insert_constraint( Point(0,i), Point(6,i));
  for (int j = 1; j < 6; ++j)
    cdt.insert_constraint( Point(j,0), Point(j,6));

  assert(cdt.is_valid());
  int count = 0;
  for (CDTplus::Subconstraint_iterator scit = cdt.subconstraints_begin();
       scit != cdt.subconstraints_end();
       ++scit)  ++count;
  std::cout << "The number of resulting constrained edges is  "
	    <<  count << std::endl;
  return 0;
}

29.10   The Triangulation Hierarchy

The class Triangulation_hierarchy_2<Tr> implements a triangulation augmented with a data structure to answer efficiently point location queries. The data structure is a hierarchy of triangulations. The triangulation at the lowest level is the original triangulation where operations and point location are to be performed. Then at each succeeding level, the data structure stores a triangulation of a small random sample of the vertices of the triangulation at the preceding level. Point location is done through a top down nearest neighbor query. The nearest neighbor query is first performed naively in the top level triangulation. Then, at each following level, the nearest neighbor at that level is found through a linear walk performed from the nearest neighbor found at the preceding level. Because the number of vertices in each triangulation is only a small fraction of the number of vertices of the preceding triangulation, the data structure remains small and achieves fast point location queries on real data. As proved in [Dev98], this structure has an optimal behavior when it is built for Delaunay triangulations. However it can be used as well for other triangulations and the class Triangulation_hierarchy_2<Tr> is templated by a parameter which is to be instantiated by one of the CGAL triangulation classes.

The class Triangulation_hierarchy_2<Tr> inherits from the triangulation type passed as template parameter Tr. The insert and remove member functions are overwritten to update the data structure at each operation. The locate queries are also overwritten to take advantage of the data structure for a fast processing.

The Vertex of a Triangulation Hierarchy

CGAL provides the class Triangulation_hierarchy_vertex_base_2<Vb> which is a model for the concept TriangulationHierarchyVertexBase_2. This class is templated by a parameter Vb which is to be instantiated by a model of the concept TriangulationVertexBase_2. The class Triangulation_hierarchy_vertex_base_2<Vb> inherits from its template parameter Vb. This design allows to use for Vb either the default vertex class or a user customized vertex class with additional functionalities.

29.10.1   Examples For the Use of a Triangulation Hierarchy

The following program is example for the standard use of a triangulation hierarchy to enhance the efficiency of a Delaunay triangulation. The program outputs the number of vertices at the different levels of the hierarchy.

File: examples/Triangulation_2/hierarchy.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Triangulation_hierarchy_2.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/algorithm.h>
#include <cassert>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Triangulation_vertex_base_2<K>             Vbb;
typedef CGAL::Triangulation_hierarchy_vertex_base_2<Vbb> Vb;
typedef CGAL::Triangulation_face_base_2<K>               Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb>      Tds;
typedef CGAL::Delaunay_triangulation_2<K,Tds>            Dt;
typedef CGAL::Triangulation_hierarchy_2<Dt>              Triangulation;
typedef Triangulation::Point                             Point;
typedef CGAL::Creator_uniform_2<double,Point>            Creator;

int main( )
{
  std::cout << "insertion of 1000 random points" << std::endl;
  Triangulation t;
  CGAL::Random_points_in_square_2<Point,Creator> g(1.);
  CGAL::copy_n( g, 1000, std::back_inserter(t));

  //verbose mode of is_valid ; shows the number of vertices at each  level
  std::cout << "The number of vertices at successive levels" << std::endl;
  assert(t.is_valid(true));

  return 0;
}

The following program shows how to use a triangulation hierarchy in conjunction with a constrained triangulation plus.

File: examples/Triangulation_2/constrained_hierarchy_plus.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Constrained_Delaunay_triangulation_2.h>
#include <CGAL/Triangulation_hierarchy_2.h>
#include <CGAL/Constrained_triangulation_plus_2.h>

#include <cassert>
#include <iostream>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Triangulation_vertex_base_2<K>             Vbb;
typedef CGAL::Triangulation_hierarchy_vertex_base_2<Vbb> Vb;
typedef CGAL::Constrained_triangulation_face_base_2<K>   Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb>      TDS;
typedef CGAL::Exact_predicates_tag                       Itag;
typedef CGAL::Constrained_Delaunay_triangulation_2<K,TDS,Itag> CDT;
typedef CGAL::Triangulation_hierarchy_2<CDT>             CDTH;
typedef CGAL::Constrained_triangulation_plus_2<CDTH>     Triangulation;

typedef Triangulation::Point                             Point;

int
main( )
{
  Triangulation cdt;
  std::cout << "Inserting a grid 5 x 5 of  constraints " << std::endl;
    for (int i = 1; i < 6; ++i)
    cdt.insert_constraint( Point(0,i), Point(6,i));
    for (int j = 1; j < 6; ++j)
    cdt.insert_constraint( Point(j,0), Point(j,6));

  int count = 0;
  for (Triangulation::Subconstraint_iterator scit = cdt.subconstraints_begin();
       scit != cdt.subconstraints_end();
       ++scit)  ++count;
  std::cout << "The number of resulting constrained edges is  ";
  std::cout <<  count << std::endl;

  //verbose mode of is_valid ; shows the number of vertices at each  level
  std::cout << "The number of vertices at successive levels" << std::endl;
  assert(cdt.is_valid(true));

  return 0;
}

29.11   Flexibility: Using Customized Vertices and Faces

To be able to adapt to various needs, a highly flexible design has been selected for 2D triangulations. We have already seen that the triangulation classes have two parameters: a geometric traits class and a triangulation data structure class which the user can instantiate with his own customized classes.

The most useful flexibility however comes from the fact that the triangulation data structure itself has two template parameters to be instantiated by classes for the vertices and faces of the triangulation. Using his own customized classes to instantiate these parameters, the user can easily build up a triangulation with additional information or functionality in the vertices and faces.

A cyclic dependency

To insure flexibility, the triangulation data structure is templated by the vertex and face base classes. Also since incidence and adjacency relations are stored in vertices and faces, the base classes have to know the types of handles on vertices and faces provided by the triangulation data structure. Thus the vertex and base classes have to be themselves parameterized by the triangulation data structure, and there is a cyclic dependency on template parameter.

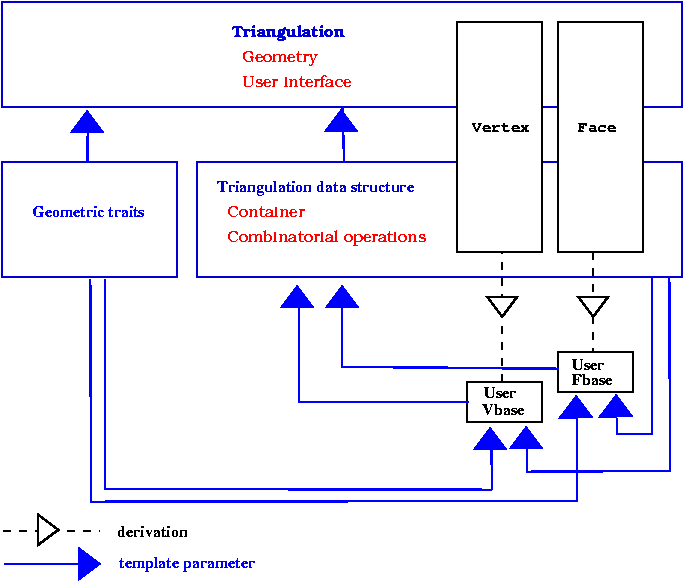
Figure 29.8:  The cyclic dependency in triangulations software design.

Previously, this cyclic dependency was avoided by using only void* pointers in the interface of base classes. These void* were converted to appropriate types at the triangulation data structure levels. This solution had some drawbacks  : mainly the user could not add in the vertices or faces of the triangulation a functionality related to types defined by the triangulation data structure, for instance a handle to a vertex, and he was lead to use himself void* pointers). The new solution to resolve the template dependency is based on a rebind mechanism similar to the mechanism used in the standard allocator class std::allocator. The rebind mechanism is described in Section 30.3 of Chapter 30. For now, we will just notice that the design requires the existence in the vertex and face base classes of a nested template class Rebind_TDS defining a type Other used by the rebinding mechanism.

The two following examples show how the user can put in use the flexibility offered by the base classes parameters.

Adding colors

The first example corresponds to a case where the user wishes to add in the vertices or faces of the triangulation an additional information that does not depend on types provided by the triangulation data structure. In that case, predefined classes Triangulation_vertex_base_with_info_2<Info,Traits,Vb> or Triangulation_face_base_with_info_2<Info,Traits,Vb> can be used. Those classes have a template parameter Info devoted to handle additional information. The following examples shows how to add a CGAL::Color in the triangulation faces.

File: examples/Triangulation_2/colored_face.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/IO/Color.h>
#include <CGAL/Triangulation_2.h>
#include <CGAL/Triangulation_face_base_with_info_2.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Triangulation_vertex_base_2<K> Vb;
typedef CGAL::Triangulation_face_base_with_info_2<CGAL::Color,K> Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb> Tds;
typedef CGAL::Triangulation_2<K,Tds> Triangulation;

typedef Triangulation::Face_handle Face_handle;
typedef Triangulation::Finite_faces_iterator Finite_faces_iterator;
typedef Triangulation::Point  Point;

int main() {
  Triangulation t;
  t.insert(Point(0,1));
  t.insert(Point(0,0));
  t.insert(Point(2,0));
  t.insert(Point(2,2));

  Finite_faces_iterator fc = t.finite_faces_begin();
  for( ; fc != t.finite_faces_end(); ++fc)  fc->info() = CGAL::BLUE;

  Point p(0.5,0.5);
  Face_handle fh = t.locate(p);
  fh->info() = CGAL::RED;

  return 0;
}

Adding handles

The second example shows how the user can still derive and plug in his own vertex or face class when he would like to have additional functionalities depending on types provided by the triangulation data structure.

File: examples/Triangulation_2/adding_handles.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Triangulation_2.h>
#include <cassert>

/* A vertex class with an additionnal handle */
template < class Gt, class Vb = CGAL::Triangulation_vertex_base_2<Gt> >
class My_vertex_base
  : public  Vb
{
  typedef Vb                              Base;
public:
  typedef typename Vb::Vertex_handle      Vertex_handle;
  typedef typename Vb::Face_handle        Face_handle;
  typedef typename Vb::Point              Point;

  template < typename TDS2 >
  struct Rebind_TDS {
    typedef typename Vb::template Rebind_TDS<TDS2>::Other    Vb2;
    typedef My_vertex_base<Gt,Vb2>                           Other;
  };

private:
  Vertex_handle  va_;

public:
  My_vertex_base() : Base() {}
  My_vertex_base(const Point & p) : Base(p) {}
  My_vertex_base(const Point & p, Face_handle f) : Base(f,p) {}
  My_vertex_base(Face_handle f) : Base(f) {}

  void set_associated_vertex(Vertex_handle va) { va_ = va;}
  Vertex_handle get_associated_vertex() {return va_ ; }
};

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef My_vertex_base<K> Vb;
typedef CGAL::Triangulation_data_structure_2<Vb> Tds;
typedef CGAL::Triangulation_2<K,Tds> Triangulation;

typedef Triangulation::Vertex_handle Vertex_handle;
typedef Triangulation::Finite_faces_iterator Finite_faces_iterator;
typedef Triangulation::Point   Point;

int main() {
  Triangulation t;
  Vertex_handle v0 = t.insert(Point(0,1));
  Vertex_handle v1 = t.insert(Point(0,0));
  Vertex_handle v2 = t.insert(Point(2,0));
  Vertex_handle v3 = t.insert(Point(2,2));

  // associate vertices as you like
  v0->set_associated_vertex(v1);
  v1->set_associated_vertex(v2);
  v2->set_associated_vertex(v3);
  v3->set_associated_vertex(v0);
  assert( v0->get_associated_vertex() == v1);

  return 0;
}

29.12   Design and Implementation History

The code of this package is the result of a long development process. Here follows a tentative list of people who added their stone to this package : Jean-Daniel Boissonnat, Hervé Brönnimann, Olivier Devillers, Andreas Fabri, Frédéric Fichel, Julia Flötotto, Monique Teillaud and Mariette Yvinec.