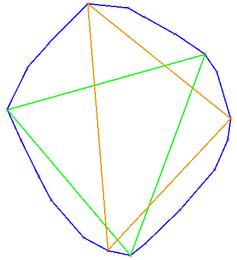
This chapter describes algorithms which for a given point set compute the ``best'' inscribed object from a specific class. We provide algorithms for computing maximal inscribed k-gons (triangles, quadrilaterals, … ) of a planar point set P. Maximal k-gons are convex, and it is known that their vertices can be chosen to be vertices of the convex hull of P. Hence, the functions CGAL::maximum_area_inscribed_k_gon_2 and CGAL::maximum_perimeter_inscribed_k_gon_2 operate on convex polygons only. The example below shows that the largest area triangle (green) and the largest perimeter triangle (orange, containing the top point) of a point set are different in general.

We further provide an algorithm for computing the maximal area inscribed axis parallel rectangle
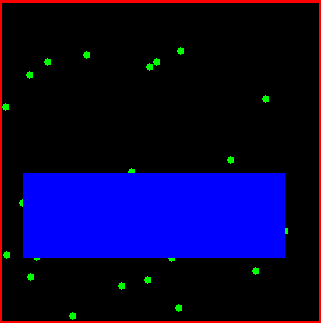
Given a set of points in the plane, the class CGAL::Largest_empty_iso_rectangle_2<T> is a data structure that maintains an iso-rectangle with the largest area among all iso-rectangles that are inside a given iso-rectangles, and that do not contain any point of the point set.
Inscribed volumes are also frequently applied to extract geometric properties of objects. The largest area triangle is for example used in heuristics for matching archaeological aerial photographs. Largest perimeter triangles are used in scoring cross country soaring flights, where the goal is basically to fly as far as possible, but still return to the departure airfield. To score simply based on the total distance flown is not a good measure, since circling in thermals allows to increase it easily.