|
CGAL 6.1 - Estimation of Local Differential Properties of Point-Sampled Surfaces
|
|
CGAL 6.1 - Estimation of Local Differential Properties of Point-Sampled Surfaces
|

Figure 85.1 Principal directions associated with \(k_{max}\) scaled by \( k_{min}\).
This package allows the estimation of local differential quantities of a surface from a point sample, given either as a mesh or as point cloud.
Note that this package needs the third party library Eigen to be installed to compile the example code..
Consider a sampled smooth surface, and assume we are given a collection of points \( P\) about a given sample \( p\). We aim at estimating the differential properties up to any fixed order of the surface at point \( p\) from the point set \( P^+ = P\cup \{ p\}\) - we denote \( N=\mid P^+\mid\). More precisely, first order properties correspond to the normal or the tangent plane; second order properties provide the principal curvatures and directions, third order properties provide the directional derivatives of the principal curvatures along the curvature lines, etc. Most of the time, estimating first and second order differential quantities is sufficient. However, some applications involving shape analysis require estimating third and fourth order differential quantities. Many different estimators have been proposed in the vast literature of applied geometry [4] (section 3, page 7), and all of them need to define a neighborhood around the point at which the estimation is computed. Our method relies on smooth differential geometry calculations, carried out on smooth objects fitted from the sample points. Datasets amenable to such a processing are naturally unstructured point clouds, as well as meshes - whose topological information may be discarded.
Estimating differential properties from discrete date always raises a philosophical issue. On one hand, estimating differential quantities subsumes a smooth surface does exist. In this spirit one wishes to recover its differential properties, so that any estimation method must come with an asymptotic convergence analysis of the results returned. For the method developed in this CGAL package, the interested will find such an analysis in [1], (Theorem 3) - it should be stressed the error bounds proved therein are optimal.
On the other hand, any estimation method may be applied to arbitrarily data - surface unknown, surface piecewise smooth etc. In such a case, no analysis can be carried out, and it is up to the users to check the results match their needs.
Unlike most of the CGAL packages, this package uses approximation methods and is not intended to provide an exact canonical result in any sense. This is why internal computations are performed with a number type possibly different from that of the input data, even if for convenience the results are returned with this original number type. A reasonable choice for this internal number type is for example the double type.
To present the method, we shall need the following notions. Consider a smooth surface. About one of its points, consider a coordinate system whose \( z\)-axis does not belong to the tangent space. In such a frame, the surface can locally be written as the graph of a bivariate function. Letting \( h.o.t.\) stand for higher order terms, one has :
\begin{equation} z(x,y)=J_{B,d}(x,y) + h.o.t. \ ; \quad J_{B,d}(x,y)=\ccSum{k=0}{d}{(\ccSum{i=0}{i}{ \frac{B_{k-i,i}x^{k-i}y^{i}}{i!(k-i)!}})}. \end{equation}
The degree \( d\) polynomial \( J_{B,d}\) is the Taylor expansion of the function \( z\), and is called its \( d\)-jet. Notice that a \( d\)-jet contains \( N_d=(d+1)(d+2)/2\) coefficients.
Recall that an umbilical point of a surface - or umbilic for short, is a point where both principal curvatures are identical. At any point of the surface which is not an umbilic, principal directions \( d_1, d_2\) are well defined, and these (non oriented) directions together with the normal vector \( n\) define two direct orthonormal frames. If \( v_1\) is a unit vector of direction \( d_1\), there exists a unique unit vector \( v_2\) so that \( (v_1,v_2,n)\) is direct; and the other possible frame is \( (-v_1,-v_2,n)\). Both these coordinate systems are known as the Monge coordinate systems. In both these systems, the surface is said to be given in the Monge form and its jet has the following canonical form :
\begin{eqnarray} z(x,y) = & \frac{1}{2}(k_1x^2 + k_2y^2)+ \frac{1}{6}(b_0x^3+3b_1x^2y+3b_2xy^2+b_3y^3) \\ & +\frac{1}{24}(c_0x^4+4c_1x^3y+6c_2x^2y^2+4c_3xy^3+c_4y^4) + h.o.t. \end{eqnarray}
The coefficients \( k_1, k_2\) are the principal curvatures, \( b_0,b_3\) are the directional derivatives of \( k_1,k_2\) along their respective curvature line, while \( b_1,b_2\) are the directional derivatives of \( k_1,k_2\) along the other curvature lines.
The Monge coordinate system can be computed from any \( d\)-jet ( \( d\geq 2\)), and so are the Monge coefficients. These information characterize the local geometry of the surface in a canonical way, and are the quantities returned by our algorithm.
Based on the above concepts, the algorithm consists of 4 steps.
Further details can be found in section Mathematical and Algorithmic Details and in [1] (section 6).
As usual, the fitting procedure may run into (almost) degenerate cases:
Due to poor sampling, the PCA used to determine a rough normal vector may not be good. The nearer this direction to the tangent plane the worse the estimation.
In these cases, even if a result is provided, the estimation may not be relevant. To inform the user of these issues, we provide the PCA results and the condition number of the fitting. In any case, it is up to the user to judge if the result meets its need.
The fitting strategy performed by the class Monge_via_jet_fitting requires the following parameters:
As explained in Section Introduction , the output consists of a coordinate system, the Monge basis, together with the Monge coefficients which are stored in the CGAL::Monge_via_jet_fitting::Monge_form class. In addition, more information on the computational issues are stored in the Monge_via_jet_fitting class.
The CGAL::Monge_via_jet_fitting::Monge_form class provides the following information.
Origin. This is the point on the fitted polynomial surface where the differential quantities have been computed. In the approximation case, it differs from the input point \( p\) : it is the projection of \( p\) onto the fitted surface following the \( z\)-direction of the fitting basis.
Monge Basis. The Monge basis \( (d_1,d_2,n)\) is orthonormal direct, and the maximal, minimal curvatures are defined wrt this basis. If the user has a predefined normal \( n_0\) (e.g. the sample points come from an oriented mesh) then if \( n_0 . n >0\) then max-min is correct; if not, i.e. \( n_0 . n <0\), the user should switch to the orthonormal direct basis \( (d_1',d_2',n')=(d_2,d_1,-n)\) with the maximal curvature \( k_1'=-k_2\) and the minimal curvature \( k_2'=-k_1\). If \( n_0 . n =0\) or is small, the orientation of the surface is clearly ill-defined, and the user may proof-check the samples used to comply with its predefined normal.
Monge Coefficients. The coefficient of the Monge form is \( (k_1, k_2 (\leq k_1), b_0, b_1, b_2, b_3, c_0, c_1, c_2, c_3, c_4)\) for \( d' = 4\).
In addition, the class Monge_via_jet_fitting stores
This concept provides the types for the input sample points, together with \( 3d\) vectors and a number type. It is used as template for the class Monge_via_jet_fitting<DataKernel, LocalKernel, SvdTraits>. Typically, one can use Cartesian< double >.
This is a parameter of the class Monge_via_jet_fitting<DataKernel, LocalKernel, SvdTraits>. This concept defines the vector and number types used for local computations and to store the PCA basis data.
Input points of type DataKernel::Point_3 are converted to LocalKernel::Point_3. For output of the CGAL::Monge_via_jet_fitting::Monge_form class, these types are converted back to DataKernel ones. Typically, one can use Cartesian< double > which is the default.
This concept provides the number, vector and matrix types for algebra operations required by the fitting method in Monge_via_jet_fitting<DataKernel, LocalKernel, SvdTraits> . The main method is a linear solver using a singular value decomposition.
To solve the fitting problem, the sample points are first converted from the DataKernel to the LocalKernel (this is done using the Cartesian_converter). Then change of coordinate systems and linear algebra operations are performed with this kernel. This implies that the number types LocalKernel::FT and SvdTraits::FT must be identical. Second the Monge basis and coefficients, computed with the LocalKernel, are converted back to the DataKernel (this is done using the Cartesian_converter and the NT_converter).
The first example illustrates the computation of the local differential quantities from a set of points given in a text file as input. The first point of the list is the one at which the computation is performed. The user has to specify a file for the input points and the degrees \( d\) and \( d'\).
File Jet_fitting_3/Single_estimation.cpp
The second example (cf Mesh_estimation.cpp in the example directory) illustrates the computation of local differential quantities for all vertices of a given mesh. The neighborhood of a given vertex is computed using rings on the triangulation. Results are twofold:
CGAL::Monge_via_jet_fitting::Monge_form and numerical information on the computation: condition number and the PCA basis; Figure 85.1 and Figure 85.2 provide illustrations of principal directions of curvature.

Figure 85.2 Principal directions of curvature and normals at vertices of a mesh of the graph of the function \( f(x,y)=2x^2+y^2\).
In this Section, we detail the mathematics involved, in order to justify the design choices made. To begin with, observe the fitting problem involves three relevant direct orthonormal basis: the world-basis \( (w_x,w_y,w_z)\), the fitting-basis \( (f_x,f_y,f_z)\), the Monge basis \( (d_1,d_2,n)\).
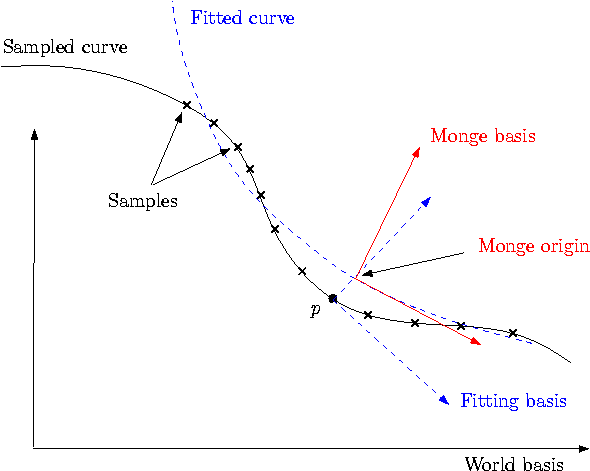
Figure 85.3 The three bases involved in the estimation.
Input: samples Output: fitting-basis
Performing a PCA requires diagonalizing a symmetric matrix. This analysis gives an orthonormal basis whose \( z\)-axis is provided by the eigenvector associated to the smallest eigenvalue.Another possibility is to choose as z-axis the axis of the world-basis with the least angle with the axis determined with the PCA. Then the change of basis reduces to a permutation of axis. Note one may have to swap the orientation of a vector to get a direct basis.
Let us denote \( P_{W\rightarrow F}\) the matrix that changes coordinates from the world-basis \( (w_x,w_y,w_z)\) to the fitting-basis \( (f_x,f_y,f_z)\). The rows of \( P_{W\rightarrow F}\) are the coordinates of the vectors \( (f_x,f_y,f_z)\) in the world-basis. This matrix represents a orthogonal transformation hence its inverse is its transpose. To obtain the coordinates of a point in the fitting-basis from the coordinates in the world-basis, one has to multiply by \( P_{W\rightarrow F}\).
As mentioned above, the eigenvalues are returned, from which the sampling quality can be assessed. For a good sampling, the eigenvector associated to the smallest eigenvalue should roughly give the normal direction.
Input: samples, fitting-basis Output: coefficients \( A_{i,j}\) of the bivariate fitted polynomial in the fitting-basis
Computations are done in the fitting-basis and the origin is the point \( p\). First, one has to transform coordinates of sample points with a translation ( \( -p\)) and multiplication by \( P_{W\rightarrow F}\).
The fitting process consists of finding the coefficients \( A_{i,j}\) of the degree \( d\) polynomial
\begin{equation} J_{A,d}= \ccSum{k=0}{d}{(\ccSum{i=0}{k}{ \frac{A_{k-i,i}x^{k-i}y^{i}}{i!(k-i)!}})}. \end{equation}
Denote \( p_i=(x_i,y_i,z_i), \ i=1,\ldots , N\) the coordinates of the sample points of \( P^+\). For interpolation the linear equations to solve are \( A(x_i,y_i)=z_i \ i=1,\ldots,N\), and for approximation one has to minimize \( \sum_{i=1}^N (A(x_i,y_i)-z_i)^2\). The linear algebra formulation of the problem is given by
\begin{eqnarray} A = & (A_{0,0}, A_{1,0},A_{0,1}, \ldots , A_{0,d})^T \\ Z= &(z_1, z_2,\ldots , z_N)^T \\ M= &(1,x_i,\ y_i,\ \frac{x_i^2}{2},\ldots , \ \frac{x_iy_i^{d-1}}{(d-1)!},\ \frac{y_i^d}{d!})_{i=1,...,N} \end{eqnarray}
The equations for interpolation become \( MA=Z\). For approximation, the system \( MA=Z\) is solved in the least square sense, i.e. one seeks the vector \( A\) such that \( A = \arg \min_A ||MA-Z||_2\).
In any case, there is a preconditioning of the matrix \( M\) so as to improve the condition number. Assuming the \( \{x_i\}\), \( \{y_i\}\) are of order \( h\), the pre-conditioning consists of performing a column scaling by dividing each monomial \( x_i^ky_i^l\) by \( h^{k+l}\) - refer to Eq. ( eqfitlinalg ). Practically, the parameter \( h\) is chosen as the mean value of the \( \{x_i\}\) and \( \{y_i\}\). In other words, the new system is \( M'Y=(MD^{-1})(DA)=Z\) with \( D\) the diagonal matrix \( D=(1,h,h,h^2,\ldots,h^d,h^d)\), so that the solution \( A\) of the original system is \( A=D^{-1}Y\).
There is always a single solution since for under constrained systems we also minimize \( ||A||_2\). The method uses a singular value decomposition of the \( N\times N_d\) matrix \( M= U S V^T\), where \( U\) is a \( N \times N\) orthogonal matrix, \( V\) is a \( N_d \times N_d\) orthogonal matrix and \( S\) is a \( N\times N_d\) matrix with the singular values on its diagonal. Denote \( r\) the rank of \( M\), we can decompose \( S= \left( \begin{array}{cc} D_r & 0_{r,\ N_d-r}\\ 0_{N-r,\ r} & 0_{N-r,\ N_d-r} \end{array} \right). \) The number \( r\), which is the number of non zero singular values, is strictly lower than \( N_d\) if the system is under constrained. In any case, the unique solution which minimize \( ||A||_2\) is given by:
\begin{equation} A= V \left( \begin{array}{cc} D_r^{-1} & 0_{N_d-r,\ r}\\ 0_{r,\ N-r} & 0_{N_d-r,\ N-r} \end{array} \right) U^TZ. \end{equation}
One can provide the condition number of the matrix \( M\) (after preconditioning) which is the ratio of the maximal and the minimal singular values. It is infinite if the system is under constrained, that is the smallest singular value is zero.
Implementation details.
We assume a solve function is provided by the traits SvdTraits. This function solves the system MX=B (in the least square sense if M is not square) using a Singular Value Decomposition and gives the condition number of M.
Remark: as an alternative, other methods may be used to solve the system. A \( QR\) decomposition can be substituted to the \( SVD\). One can also use the normal equation \( M^TMX=MTB\) and apply methods for square systems such as \( LU\), \( QR\) or Cholesky since \( M^TM\) is symmetric definite positive when \( M\) has full rank. The advantages of the \( SVD\) is that it works directly on the rectangular system and gives the condition number of the system. For more on these alternatives, see [3] (Chap. 5).
Input: coefficients of the fit \( A_{i,j}\), fitting-basis
Output: Monge basis wrt fitting-basis and world-basis
In the fitting basis, we have determined a height function expressed by Eq. ( eqanswer ). Computations are done in the fitting-basis. The partial derivatives, evaluated at \( (x,y)=(0,0)\), of the fitted polynomial \( J_{A,d}(x,y)\) are \( A_{i,j}=\frac{\partial^{i+j}J_{A,d}}{\partial^ix \partial^jy}\) Expanding Eq. ( eqanswer ) yields:
\begin{eqnarray} J_{A,d}(x,y)&= A_{0,0}+A_{1,0}x+A_{0,1}y+\frac{1}{2}(A_{2,0}x^2+2A_{1,1}xy+A_{0,2}y^2) + \frac{1}{6}(A_{3,0}x^3+3A_{2,1}x^2y+\ldots )+ \ldots \end{eqnarray}
Input: coefficients of the fit, Monge basis wrt fitting-basis ( \( P_{F \rightarrow M}\))
Output: third and fourth order coefficients of Monge
We use explicit formula. The implicit equation of the fitted polynomial surface in the fitting-basis with origin the point \( (0,0,A_{0,0})\) is \( Q=0\) with
\begin{equation} Q=-w-A_{0,0} +\ccSum{i,j}{}{\frac{A_{i,j}u^iv^j}{i!j!}}. \end{equation}
The equation in the Monge basis is obtained by substituting \( (u,v,w)\) by \( P^T_{F\rightarrow M}(x,y,z)\). Denote \( f(x,y,z)=0\) this implicit equation. By definition of the Monge basis, we have locally (at \( (0,0,0)\))
\begin{equation} f(x,y,z)=0 \Leftrightarrow z=g(x,y) \end{equation}
and the Taylor expansion of \( g\) at \( (0,0)\) are the Monge coefficients sought. Let us denote the partial derivatives evaluated at the origin of \( f\) and \( g\) by \( f_{i,j,k}=\frac{\partial^{i+j+k}f}{\partial^ix \partial^jy \partial^kz}\) and \( g_{i,j}=\frac{\partial^{i+j}g}{\partial^ix \partial^jy}\). One has \( f_{1,0,0}=f_{0,1,0}=f_{1,1,0}=0\), \( g_{0,0}=g_{1,0}=g_{0,1}=g_{1,1}=0\) and \( g_{2,0}=k_1\), \( g_{0,2}=k_2\). The partial derivative of order \( n\) of \( f\) depends on the matrix \( P_{F\rightarrow M}\) and the partial derivatives of order at most \( n\) of \( J_{A,d}\). The third and fourth order coefficients of are computed with the implicit function theorem. For instance:
\begin{eqnarray*} &b_0=g_{3,0}=-{\frac { f_{3,0,0} f_{0,0,1} -3\, f_{1,0,1} f_{2,0,0} }{ f_{0,0,1} ^{2}}} \\ &b_1=g_{2,1}=-{\frac {- f_{0,1,1} f_{2,0,0} + f_{2,1,0} f_{0,0,1} }{ f_{0,0,1} ^{2}}} \\ & .... \end{eqnarray*}