User Manual

Authors

Sven Oesau and Florent Lafarge

Introduction

This CGAL component implements the kinetic space partition proposed by Bauchet et. al [1]. It takes as input a set of non-coplanar convex polygons and partitions the bounding box of the input into polyhedra, where each polyhedron and its facets are convex. Each facet of the partition is part of the input polygons or an extension of them.

The kinetic partition homogeneously expands each input polygon along its support plane until collisions occur between them. At each collision, their expansion may stop, they may restrict the propagation along an intersection line between two support planes or they may continue beyond the intersection line. The polygons are split at the beginning of the kinetic simulation and at each collision along the intersection line to be intersection-free.

Whether a polygon is expanded beyond an intersection with another polygon, depends on the user specified k parameter. Choosing k = 1 will cause the expansion of polygons to locally stop at the first intersection with another polygon and choosing k equal to the number of input polygons will lead to a full expansion of each polygon to the bounding box.

Algorithm

The first step of the method creates a plane arrangement between the support planes of the input polygons. The computation of a plane arrangement has \(O(n^3)\). To speed up the computation the input data can be decomposed into separate kinetic partitions using an octree. The decomposition limits the expansion of an input polygon to octree nodes it initially intersects. The usage of an octree significantly speeds up the creation of the kinetic partition. However, it adds facets to the partition which originate from the octree and do not belong to an input polygon. The plane arrangement contains all points and lines of the intersections between the support planes and the bounding box. For each support plane, all intersections with the bounding box and other support planes are given by lines, edges and vertices of the arrangement. The kinetic partition created in the second step is a subset of faces of the arrangement depending on the k parameter.

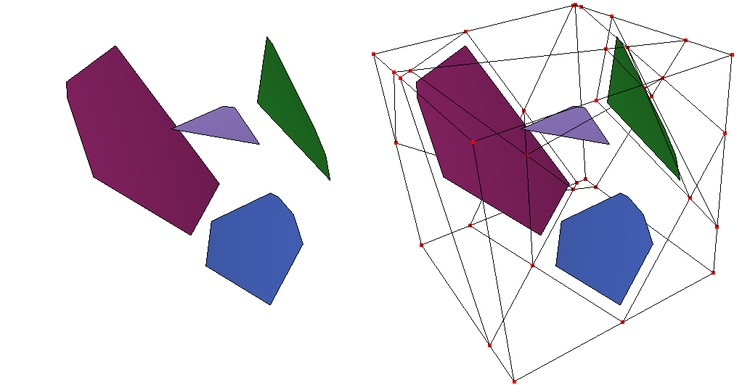
Figure 68.1 Plane arrangement.
Left: 4 convex polygons as input. Right: plane arrangement and bounding box together with input.

The kinetic partition for a chosen k is obtained by propagating each polygon within its support plane. As intersections with other polygons can only occur at the known edges in the plane arrangement, the 3D collision problem can be solved as separate 2D polygon edge collisions.

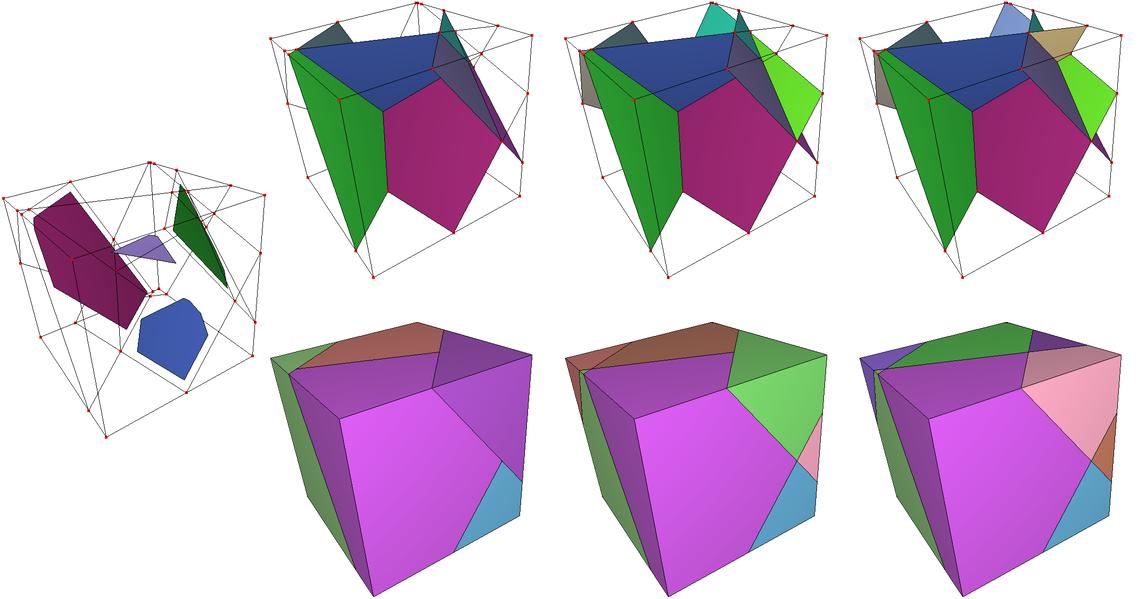
Figure 68.2 Impact of k parameter on partition.
Left: Arrangement with 4 input polygons. Right: three columns with propagated polygons on top and volumes of kinetic partition on bottom for k = 1, k = 2 and k = 3 from left to right with 5, 8 and 12 created volumes respectively.

Parameters

The algorithm has five parameters:

• k: unsigned int
  The main parameter of this method is k, the maximum number of intersections that can occur for a polygon before its expansion stops. The initial intersections of the original input polygons are not considered. Thus increasing the k leads to a higher complexity of the partitioning, i.e., a higher number of facets and a higher number of volumes. For a certain k the partition can be considered to be complete and an increase in k will not further increase the complexity of the partition. A typical choice of k is in the range of 1 to 3.
• reorient_bbox: boolean
  The default bounding box of the partition is axis-aligned. Setting reorient_bbox to true aligns the x-axis of the bounding box with the direction of the largest variation in horizontal direction of the input data while maintaining the z-axis.
• bbox_dilation_ratio: FT
  By default the size bounding box of the input data is increased by 10% to avoid that input polygons are coplanar with the sides of the bounding box.
• max_octree_node_size: unsigned int
  A kinetic partition is split into 8 subpartitions using an octree if the number of intersecting polygons is larger than specified. The default value is 40 polygons.
• max_octree_depth: unsigned int
  Limits the maximum depth of the octree decomposition. A limitation is necessary as arbitrary dense polygon configurations exist, e.g., a star. The default value is set to 3.

Result

The kinetic partition can be accessed as a LinearCellComplex via CGAL::Kinetic_space_partition_3::get_linear_cell_complex().

Examples

The following example reads a set of polygons from a file and creates a kinetic partition. Increasing the k parameter to 2 or 3 leads to a more detailed kinetic partition.

File Kinetic_space_partition/kinetic_partition.cpp

#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Kinetic_space_partition_3.h>
#include <CGAL/Real_timer.h>
#include <CGAL/IO/polygon_soup_io.h>
 
using EPICK = CGAL::Exact_predicates_inexact_constructions_kernel;
using EPECK = CGAL::Exact_predicates_exact_constructions_kernel;
 
using Kernel     = EPICK;
using FT         = typename Kernel::FT;
using Point_3    = typename Kernel::Point_3;
 
using Surface_mesh = CGAL::Surface_mesh<Point_3>;
using KSP          = CGAL::Kinetic_space_partition_3<EPICK>;
using Timer        = CGAL::Real_timer;
 
int main(int argc, char** argv)
{
  // Reading polygons from file
  std::string input_filename = (argc > 1 ? argv[1] : "data/test-4-rnd-polygons-4-6.off");
  std::ifstream input_file(input_filename);
 
  std::vector<Point_3> input_vertices;
  std::vector<std::vector<std::size_t> > input_faces;
 
  if (CGAL::IO::read_polygon_soup(input_filename, input_vertices, input_faces)) {
    std::cout << "* reading the file: " << input_filename << "!" << std::endl;
    input_file.close();
  } else {
    std::cerr << "ERROR: can't read the file " << input_filename << "!" << std::endl;
    return EXIT_FAILURE;
  }
 
  std::cout << "--- INPUT STATS: \n* number of polygons: " << input_faces.size() << std::endl;
 
  // Parameters.
  const unsigned int k = (argc > 2 ? std::atoi(argv[2]) : 1);
 
  // Initialization of Kinetic_space_partition_3 object.
  // 'debug' set to true exports intermediate results into files in the working directory.
  // The resulting volumes are exported into a volumes folder, if the folder already exists.
  KSP ksp(CGAL::parameters::verbose(true).debug(false));
 
  // Providing input polygons.
  ksp.insert(input_vertices, input_faces);
 
  Timer timer;
  timer.start();
 
  // 'initialize' creates the intersection graph that is used for the partition.
  ksp.initialize(CGAL::parameters::bbox_dilation_ratio(1.1).reorient_bbox(false));
 
  // Creating the partition with allowing up to 'k' intersections for each kinetic polygon.
  ksp.partition(k);
 
  timer.stop();
  const FT time = static_cast<FT>(timer.time());
 
  // Access the kinetic partition via linear cell complex.
  typedef CGAL::Linear_cell_complex_traits<3, EPECK> LCC_Traits;
  CGAL::Linear_cell_complex_for_combinatorial_map<3, 3, LCC_Traits, typename KSP::Linear_cell_complex_min_items> lcc;
  ksp.get_linear_cell_complex(lcc);
 
  std::vector<unsigned int> cells = { 0, 2, 3 }, count;
  count = lcc.count_cells(cells);
 
  std::cout << "For k = " << k << ":\n" << " vertices: " << count[0] << "\n faces: " << count[2] << "\n volumes: " << count[3] << std::endl;
 
  std::cout << "\n3D kinetic partition created in " << time << " seconds!" << std::endl;
 
  return EXIT_SUCCESS;
}

Design and Implementation History

This package is an implementation of Bauchet et. al [1] with an octree replacing the grid subdivision. A proof of concept of the kinetic partition was developed by Simon Giraudot and Dmitry Anisimov.