|
CGAL 4.7 - Kinetic Framework
|
|
CGAL 4.7 - Kinetic Framework
|
This chapter describes a framework for implementing kinetic data structures and sweepline algorithms. If you just would like to use existing kinetic data structures, please read Chapter Kinetic Data Structures instead. Readers wishing to brush up on their familiarity with kinetic data structures or better understand the terminology we use should read Section An Overview of Kinetic Data Structures and Sweep Algorithms of that chapter. A brief overview of the framework can be found in Section An Overview of the Kinetic Framework (also of that chapter) and it too is recommended reading. Here we dive right in to discussing to discussing the architecture of the framework in Section Architecture and finally we give several examples of using the framework to implement a kinetic data structure in Section Examples. The framework makes heavy use of our Polynomial_kernel package to provide models of the Kinetic::FunctionKernel concept.
The framework was first presented at ALENEX [1].
This package provides a framework to allow exact implementation of kinetic data structures and sweepline algorithms. Below we discuss in detail each one of the first four major concepts which help in implementing kinetic data structures: the Kinetic::Simulator, the Kinetic::Kernel, the Kinetic::ActiveObjectsTable and the Kinetic::InstantaneousKernel. The Kinetic::FunctionKernel concept is discussed separately in Section Algebraic Kernel.
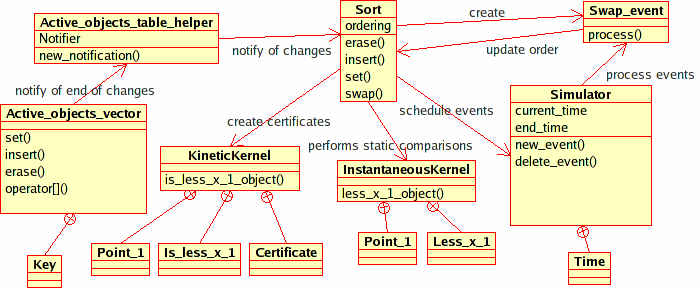
Kinetic::Sort<Traits, Visitor> kinetic data structure and the various pieces of our framework. Other, more complicated, kinetic data structures will also use the Kinetic::InstantaneousKernel in order to insert/remove geometric primitives and audit themselves. Kinetic::Sort<Traits, Visitor> uses the sorting functionality in STL instead. The Kinetic::Simulator is the central repository of all active events. It maintains the event queue and can use its knowledge of the events in the queue to find times for the kinetic data structures to easily check their own correctness (this will be discussed in more detail later in this section). Kinetic data structures call methods of the Kinetic::Simulator to schedule new events, deschedule old ones and access and change data contained in already scheduled events (the operations on existing events are performed using a key which was returned when the event was scheduled). For controlling the simulation, methods in the Kinetic::Simulator allow stepping through events, advancing time and even running the simulation backwards (that is we run the simulation with the time running in the opposite direction).
The kinetic sorting example in Figure A Simple Example shows the basic usage of the Kinetic::Simulator. First, the Simulator is created by the Kinetic::SimulationTraits. The kinetic data structure gets a handle to the simulator from the traits class and uses the handle to add its events to the simulation. The Kinetic::Simulator is then told to advance time up until the end of the simulation, processing all events along the way.
Each event is represented by a Kinetic::Simulator::Time and an instance of a model of the Kinetic::Simulator::Event concept. Models of the Kinetic::Simulator::Event concept are responsible for taking the appropriate action in order to handle the kinetic event they represent. Specifically, the Kinetic::Simulator::Event concept specifies one method, Kinetic::Simulator::Event::process(), that is called when the event occurs. The body of the Kinetic::Simulator::Event::process() method typically simply calls a method of the kinetic data structure that created the event; for example in our kinetic sorting example, processing an event means calling the Kinetic::Sort<Traits, Visitor>::swap() method of the kinetic sorting data structure.
In the model of the Kinetic::Simulator concept that we provide, Kinetic:Default_simulator<FunctionKernel, EventQueue>, any model of the Kinetic::Simulator::Event concept can be inserted as an event. This ability implies that events can be mixed at run time, which is essential when we want to support multiple kinetic data structures operating on the same set of moving geometric primitives.
The Kinetic::Simulator::Time concept is defined by the simulator, typically to be some representation of a root of a polynomial, taken from the Kinetic::FunctionKernel (details of the algebraic side of the package will be discussed in Section Algebraic Kernel). For most kinetic data structures Kinetic::Simulator::Time only needs to support comparisons (we need to compare events, in order to process them in the correct order) and a few other non-arithmetic operations.
When the failure times of certificates are sorted exactly (as opposed to when we numerically approximate the roots of the certificate polynomials) the correctness of kinetic data structures can be easily verified. Let \( I\) be an open interval between the last event processed and the next event to be processed. As was mentioned in the introduction kinetic data structures do not change combinatorially in \( I\). In addition, although the static data structures can be degenerate at the roots defining the two ends of the interval, they are not, in general, degenerate in the interior. An independent check of the integrity of kinetic data structures can be provided by, for example, using an Kinetic::InstantaneousKernel (cf. Subsection The Kinetic::InstantaneousKernel) to rebuild the static version of the structure from scratch at some time interior to \( I\) and compare it to the kinetic version. This auditing can typically catch algorithmic or programming errors much closer to the time they arise in the simulation than, for example, using visual inspection. Such easy auditing is one of the powerful advantages of having an exact computational framework since, as with static data structures, when using inexact computations differentiating between errors of implementation and numeric errors is quite tricky.
Kinetic data structures receive alerts of appropriate times to audit themselves using a notification framework. The same framework is also used by the Kinetic::ActiveObjectsTable to alert kinetic data structures when the set of primitives changes (see Subsection The Kinetic::ActiveObjectsTable). To use the notification framework, the kinetic data structure creates a proxy object which implements a standard Listener interface. It then registers this proxy with the Kinetic::Simulator. When the Kinetic::Simulator finds an appropriate time for the kinetic data structures to audit themselves it calls the function Listener::new_notification(Type) on each of the registered proxy objects. A helper for creating such proxy objects, called Kinetic::Simulator_kds_listener<Listener, KDS>, is provided by the framework. It translates the notification into a function call (audit()) on the kinetic data structure. Pointers in the notification framework are reference counted appropriately to avoid issues caused by the creation and destruction order of kinetic data structures and the simulator. See Section Runtime event passing for a more complete discussion of this part of the framework.
Internally the Kinetic::Simulator maintains a priority queue containing the scheduled events. The type of the priority queue is a template argument to our Kinetic::Simulator model and, as such, it can be replaced by the user. In our package, we provide two different types of priority queues, a heap and a two-list priority queue. A two-list queue is a queue in which there is a sorted front list, containing all events before some time and an unsorted back list. The queue tries to maintain a small number of elements in the front list, leaving most of them in the unsorted main pool. The two-list queue, although an unconventional choice, is our default queue when using exact computation because it minimizes comparisons involving events that are far in the future. These events are likely to be deleted before they are processed, so extra work done structuring them is wasted. Our experiments have shown that, for example, the two-list queue causes a 20% reduction in running time relative to a binary heap for Delaunay triangulations with degree 3 polynomial motions and 20 points.
The Kinetic::Kernel is structured very much like static CGAL kernels. It defines a number of primitives, which in the model provided are Kinetic::Kernel::Point_1, Kinetic::Kernel::Point_2, Kinetic::Kernel::Point_3 and Kinetic::Kernel::Weighted_point_3. The primitives are defined by a set of Cartesian coordinates each of which is a function of time, a Kernel::MotionFunction. In addition it defines constructions and certificate generators which act on the primitives. The certificate generators are the direct analog of the non-kinetic predicates. Each certificate generator take a number of primitives as arguments, but instead of producing an element from a discrete set they produce a set of discrete failure times for the certificate. These failure times are wrapped in a model of Kinetic::Certificate.
A Kinetic::Certificate is a simple object whose primary function is to produce a Kinetic::Simulator::Time object representing the failure time of the certificate. Since, the handling of most certificate failures involves creating a new certificate whose certificate function is the negation of the old certificate function, a Kinetic::Certificate object caches any work that could be useful to isolate future roots of the certificate function (such as the Sturm sequence of the certificate function). To illustrate this further, if you have two one-dimensional points with coordinate functions \( p_0(t)\) and \( p_1(t)\), the certificate that the first moving point is after the second corresponds to the inequality \( p_0(t) - p_1(t) > 0\). When the certificate fails and the two points cross, the new certificate is \( p_1(t)- p_0(t) > 0\), which is the negated version of the certificate just processed and which has the same roots.
The model of Kinetic::Kernel provided includes the certificate generators necessary for Delaunay triangulations (in one, two and three dimensions) and regular triangulations (in 3D). New certificates can be fairly easily added. An example is included in the distributed code.
The Kinetic::ActiveObjectsTable stores a set of kinetic primitives. Its purpose is to notify kinetic data structures when new primitives are added, when primitives are removed or when a trajectories change. Each primitive is uniquely identified by a Key, assigned by the table when the primitive is added, that can be used to change or remove it. We provide one model of the Kinetic::ActiveObjectsTable concept, called Kinetic::Active_objects_vector<MovingObject> which stores all the moving primitives in an std::vector<D>.
Notifications of changes to the set of active objects are handled using a setup similar to the Kinetic::Simulator audit time notification. We provide a helper class, Kinetic::Active_objects_listener_helper<ActiveObjectsTable, KDS>, which translates the notifications into insert(Key), erase(Key) or set(Key) function calls on the kinetic data structure.
The Kinetic::InstantaneousKernel allows existing CGAL data structures to be used on moving data as it appears at some instant of time. Models of this concept are, by definition, models of a CGAL Kernel or a traits class, and, therefore, can then be used as the traits class of CGAL's algorithms and data structures.
Consider for example the kinetic Delaunay data structure in either two or three dimensions. Internally, it uses a Delaunay_triangulation_2<Traits, Tds> or Delaunay_triangulation_3<Traits, Tds> to represent the triangulation, instantiated with a model of the Kinetic::InstantaneousKernel concept as its traits class. At initialization, as well as at times during the simulation when we want to insert a point to the kinetic Delaunay triangulation, a static version of the Delaunay triangulation is conceptually instantiated. More precisely, the time for the copy of the model of the Kinetic::InstantaneousKernel stored in the CGAL triangulation is set to be the current time (or rather, as discussed in the introduction, a more convenient time determined by the Kinetic::Simulator combinatorially equivalent to the current time). The kinetic data structure then calls the Delaunay_triangulation_3<Traits, Tds>::insert(Point) insert method to insert the point. The static insert method called uses various predicate functors on the moving points which evaluate to the values that the predicates have at that instant in time. Removal is handled in an analogous manner. Auditing of the geometric structure is easily handled in a similar manner (in the case of Delaunay triangulations by simply calling the verify() method after setting the time).
We describe some coding conventions used, graphical display, notification and reference management support in the framework in the following sections.
A number of objects need to maintain pointers to other independent objects. For example, each kinetic data structure must have access to the Kinetic::Simulator so that it can schedule and deschedule events. These pointers are all reference counted in order to guarantee that they are always valid. We provide a standard reference counting pointer and object base to facilitate this, namely Ref_counted<Object>.
Each shared object in the framework defines a type Handle which is the type for a reference counter pointer pointing to it. These should be used for storing pointers to the objects in order to avoid dangling pointers. In addition, many of the objects expect such pointers as arguments.
Runtime events must be passed from notifiers, namely the Kinetic::ActiveObjectsTable and the Kinetic::Simulator to listeners, typically the kinetic data structures. For example, kinetic data structures are notified when new primitives are added to the Kinetic::ActiveObjectsTable. On reciving the notification, it will add the new primitive to the combinatorial structure it is maintaining. The events are passed using a simple, standardized notification interface. To receive notifications, the listener first defines a small proxy class which inherits from a Listener base type provided by the notifier. On creation, the Listener base class registers itself with the notifier on construction (and unregisters itself on destruction).
When the some state of the notifier changes, it calls the new_notification method on the listener proxy object provided and passes it a label corresponding to the name of the field that changed. The proxy object can then call an appropriate method on the kinetic data structure or whetever the listening class is.
In order to unregister on destruction, the Listener must store a (reference counted) pointer to the object providing notifications. This pointer can be accessed through the notifier() field. The Listener object stores a reference counted pointer to the notifying object, while the notifying object stores a plain pointer to the Listener. It can do this since the Listener is guaranteed to unregister itself when it is destroyed. This avoids circular reference counted pointers as well as dangling pointers.
The interface between the algebraic kernel and the kinetic data structures package was kept quite minimal in order to ease the implementation of various underlying computation models. The interface is detailed in the reference page (Kinetic::FunctionKernel).
We provide models of the algebraic kernel that handle polynomial Kinetic::Function objects. The provided models perform
The exact models, which we implement the numerics for, handle non-square-free polynomials and polynomials with arbitrary field number type coefficients and are quite robust.
There are several modifications we can make to how the roots are handled to optimize for the case of kinetic data structures. The first are motivated by the question of how to handle degeneracies (certificate functions which have roots at the same time). Naively, there is no way to differentiate between a certificate which fails immediately when it is created and one whose function is momentarily 0, but will be valid immediately in the future. In order to handle such degeneracies we ensure that all the certificate function generators produce certificate functions which are positive when the corresponding certificates are valid. Then, if we have a degeneracy we can differentiate between a certificate which fails immediately and one which is simply degenerate by looking at the sign of the certificate function immediately following the root (equivalently, by looking at the derivative). In addition, this allows us, under the assumption that computations are performed exactly, to check that all certificates are not invalid upon creation.
The assumption that certificates are positive when valid is particular useful when using numeric solvers. Without it there is no reliable way to tell whether a root near the current time is the certificate having become valid just before the current time, or failing shortly in the future. Testing the sign of the function immediately after the root reliably disambiguates the two cases.
In addition, we have to specially handle even roots of functions. For the most part these can just be discarded as dropping an even root is equivalent to perturbing the simulation to remove the degeneracy. However, when we are using the Kinetic::Simulator to audit the kinetic data structures, they most be broken up in to two, equal, roots to avoid auditing at the degeneracy.
We provide a number of examples of different levels of usage of the kinetic data structures framework, both for kinetic data structures as well as sweepline algorithms.
To see how to use existing kinetic data structures, look at the examples in the previous chapter such as Section A Simple Example.
The here we cover implementing kinetic data structures. The examples explained are
In order to see more detail about how to implement a kinetic data structure, the best place to start is the source code for the kinetic sorting data structure, Kinetic::Sort<Traits, Visitor>. Once you are familiar with that, Kinetic::Delaunay_2<Traits, Triangulation, Visitor> is the next step in complexity.
We will first explain in detail how a typical kinetic data structure uses the various pieces of the framework, then move on to showing the actual code for a simpler data structure.
Here we will explain how the kinetic sorting data structure uses the various pieces of the package. A schematic of its relationship to the various components is shown in the UML diagram in Figure 84.1. In this subsection we abuse, for reasons of simplicity of presentation, the concept/model semantics: when we refer to concepts we actually refer to an instance of a model of them.
As with most kinetic data structures, Kinetic::Sort<Traits, Visitor> maintains some sort of combinatorial structure (in this case a sorted doubly linked list), each element of which has a corresponding certificate in the event queue maintained by the simulator. In the case of sorting, there is one certificate maintained for each "edge" between two consecutive elements in the list.
On creation, the data structure is passed a copy of the Kinetic::SimulationTraits for this simulation, which it saves for future use. It gets a handle to to the Kinetic::ActiveObjectsTable by calling the Kinetic::SimulationTraits::active_points_1_table_handle() method and registers a proxy with the table in order to receive notifications of changes to the point set. The Kinetic::SimulationTraits method returns a handle to, rather than a copy of, the Kinetic::ActiveObjectsTable, since the table must be shared between all the kinetic data structures using these points. The handles are reference counted pointers, thus saving the user from worrying about cleaning things up properly.
When new points are added to the model of the Kinetic::ActiveObjectsTable, the table calls the new_notification() method on the proxy of the kinetic data structure, which in turn calls the insert(Point_key) method of the kinetic data structure. The Point_key here is the key which uniquely identifies the newly inserted point in the table. The data structure then requests an instance of a model of the Kinetic::InstantaneousKernel from the Kinetic::SimulationTraits. It sets the time on the instantaneous kernel to the time value gotten from the Kinetic::Simulator::current_time_nt() method. This method returns a field number type that is between the previous and next event, as discussed in the introduction. An instance of the Kinetic::InstantaneousKernel::Compare_x_1 predicate (wrapped in order to make it return less) and the STL function std::upper_bound() are then used to insert the new point in the sorted list. For each inserted object, the kinetic data structure removes the no longer relevant certificate from the event queue by calling the Kinetic::Simulator::delete_event(Key) function and creates two new certificates using a Kinetic::Kernel::Compare_x_1 certificate functor. The new certificates are inserted in the event queue by calling the Kinetic::Simulator::new_event(Time, Event) method where Kinetic::Simulator::Event is a proxy object which instructs the sort kinetic data structure to swap two points when its process() method is called.
Now that the kinetic data structure has been initialized, the simulator is instructed to process all events. Each time an event occurs, the simulator calls the process() method on the corresponding proxy object. The proxy, in turn, tells the sort kinetic data structure to swap the two points whose order has changed.
The Kinetic::Simulator can periodically instruct the kinetic data structures to audit themselves. As is explained in Section The Kinetic::Simulator, a proxy object maps the notification on to an audit() function call in the kinetic data structure. To audit itself the kinetic data structure builds a list of all the current points and uses std::sort to sort this list using a comparison function gotten from the Kinetic::InstantaneousKernel. This sorted list is compared to the maintained one to verify correctness. This auditing could also have been done by evaluating the Kinetic::InstantaneousKernel predicate for each sorted pair. Since auditing a kinetic data structure typically requires at least linear time in the size of the combinatorial structure, the auditing procedure in between events is deactivated by default. The user can however easily switch it on by defining the CGAL_CHECK_EXACTNESS and CGAL_CHECK_EXPENSIVE CGAL macros.
This general structure of the interaction between the kinetic data structure and the framework is shared by all of the provided kinetic data structures and has proved itself to go quite far.
To show how to implement such things, instead of presenting a full kinetic data structure, we present a trivial one which maintains one event in the queue which maintains one event in the queue, scheduled to occur one time unit after the last change was made to the set of active primitives. Two classes are defined, the Trivial_event, and the Trivial_kds. The event classes must be declared outside of the kinetic data structure so that the operator<< can be defined for them.
The kinetic data structure maintains the invariant that it was one event in the queue at all times. This event ccurs one time unit after the last event or change in the set of objects occurs. As a result, the kinetic data structure has the main parts of a real one-it responds to changes in trajectories of the objects and certificate failures (when the event expires).
The public methods can be grouped into three sets which are shared with almost all other kinetic data structures:
has_certificates and set_has_certificates which checks/sets whether the kinetic data structure is currently maintaining certificates. insert, set, erase which are called by the Kinetic::Active_objects_listener_helper in response to the addition, modification, or deletion of an object to, in or from the simulation. audit which is called periodically by the Kinetic::Simulator_kds_listener when kinetic data structures can easily audit themselves. In addition, it has one method which is called when a certificate fails. The name/existence of such methods depend on the nature of the kinetic data structure in question.
Like many kinetic data structures, it takes a Kinetic::SimulationTraits as a template argument. This traits class defines the types needed for the simulation and is responsible for instantiating them.
The following example shows how to add a new type of certificate to a simulation.
First we code the actual certificate function generator. It must take some sort (or sorts) of kinetic primitives, compute some function from their coordinates.
Then we define a kinetic kernel which includes this predicate. To do this we wrap the function generator generator in a Kinetic::Certificate_generator<Kernel, Generator>. This wrapper uses the generator to create the certificate function and then the Kinetic::FunctionKernel to solve the certificate function. The result is wrapped in a Kinetic::Certificate object.
Now we have the unfortunately rather messy part of assembling a new Kinetic::SimulationTraits model. This is done in two steps for convenience.
Now the simulation traits can be used by a kinetic data structure. Note that we define active point table for all dimensions. This is needed by the Kinetic::InstantaneousKernel, even if they are not used.