|
CGAL 4.7 - Kinetic Data Structures
|
|
CGAL 4.7 - Kinetic Data Structures
|
Lets say you want to maintain a sorted list of items (each item is associate with a real number key). You can imagine placing each of the items on the point on the real line corresponding to its key. Now, let the key for each item change continuously (i.e. no jumps are allowed). As long as no two (consecutive) items cross, the sorted order is intact. When two items cross, they need to be exchanged in the list and then the sorted order is once again correct. This is a trivial example of a kinetic data structure. The key observation is that the combinatorial structure which is maintained changes at discrete times (events) even though the basic building blocks are changing continuously.
This chapter describes a number of such kinetic data structures implemented using the Kinetic framework described in Chapter Kinetic Framework. We first, in Section An Overview of Kinetic Data Structures and Sweep Algorithms introduce kinetic data structures and sweepline algorithms. This section can be skipped if the reader is already familiar with the area. The next sections, Section Terms Used and Section An Overview of the Kinetic Framework introduce the terms and give an overview of the framework. They are recommended reading for all readers, even if you are just using provided kinetic data structures. We then present kinetic data structures for Delaunay triangulations in two and three dimensions in Section Using Kinetic Data Structures.
If you are already familiar with kinetic data structures and know what you want to do, you might want to first take a look at the next section Section Quick Hints which covers quick hints.
This section gives quick answers to some questions people might have. It presumes knowledge of kinetic data structures and this framework.
See the example Kinetic_framework/defining_a_simulation_traits.cpp to see how to define a new SimulationTraits class where the Active-Objects-Table contains extra data along with the point.
We provide two simple kinetic data structures, first most trivial is Kinetic_framework/trivial_kds.cpp and a slightly more complicated one is:
Defined in CGAL/Kinetic/Sort.h
We are working on that one, but you will have to wait.
Kinetic data structures were first introduced in by Basch et. al. in 1997 [1]. The idea stems from the observation that most, if not all, computational geometry structures are built using predicates - functions on quantities defining the geometric input (e.g. point coordinates), which return a discrete set of values. Many predicates reduce to determining the sign of a polynomial on the defining parameters of the primitive objects. For example, to test whether a point lies above or below a plane we compute the dot product of the point with the normal of the plane and subtract the plane's offset along the normal. If the result is positive, the point is above the plane, zero on the plane, negative below. The validity of many combinatorial structures built on top of geometric primitives can be verified by checking a finite number of predicates of the geometric primitives. These predicates, which collectively certify the correctness of the structure, are called certificates. For a Delaunay triangulation in three dimensions, for example, the certificates are one InCircle test per facet of the triangulation, plus a point plane orientation test for each facet or edge of the convex hull.
The kinetic data structures approach is built on top of this view of computational geometry. Let the geometric primitives move by replacing each of their defining quantities with a function of time (generally a polynomial). As time advances, the primitives trace out paths in space called trajectories. The values of the polynomial functions of the defining quantities used to evaluate the predicates now also become functions of time. We call these functions certificate functions. Typically, a geometric structure is valid when all predicates have a specific non-zero sign. In the kinetic setting, as long as the certificate functions maintain the correct sign as time varies, the corresponding predicates do not change values, and the original data structure remains correct. However, if one of the certificate functions changes sign, the original structure must be updated, as well as the set of certificate functions that verify it. We call such occurrences events.
Maintaining a kinetic data structure is then a matter of determining which certificate function changes sign next, i.e. determining which certificate function has the first real root that is greater than the current time, and then updating the structure and the set of certificate functions. In addition, the trajectories of primitives are allowed to change at any time, although \( C^0\)-continuity of the trajectories must be maintained. When a trajectory update occurs for a geometric primitive, all certificates involving that primitive must be updated. We call the collection of kinetic data structures, primitives, event queue and other support structures a simulation.
Sweepline algorithms for computing arrangements in \( d\) dimensions easily map on to kinetic data structures by taking one of the coordinates of the ambient space as the time variable. The kinetic data structure then maintains the arrangement of a set of objects defined by the intersection of a hyperplane of dimension \( d-1\) with the objects whose arrangement is being computed.
Time is one of the central concepts in a kinetic simulation. Just as static geometric data structures divide the continuous space of all possible inputs (as defined by sets of coordinates) into a discrete set of combinatorial structures, kinetic data structures divide the continuous time domain into a set of disjoint intervals. In each interval the combinatorial structure does not change, so, in terms of the combinatorial structure, all times in the interval are equivalent. We capitalize on this equivalence in the framework in order to simplify computations. If the primitives move on polynomial trajectories and the certificates are polynomials in the coordinates, then events occur at real roots of polynomials of time. Real numbers, which define the endpoints of the interval, are more expensive to compute with than rational numbers, so performing computations at a rational number inside the interval is preferable whenever possible. See Section The Kinetic::InstantaneousKernel for an example of where this equivalence is exploited.
The provided kinetic data structures are implemented on top of the Kinetic framework presented in Chapter Kinetic Framework. It is not necessary to know the details of the framework, but some familiarity is useful. Here we presented a quick overview of the framework.
The framework is structured around five main concepts. See Figure 83.1 for a schematic of how a kinetic data structure interacts with the various parts. The main concepts are
Kinetic::Simulator. Models of this concept process events in the correct order and audit kinetic data structures. There should be one instance of a model of this concept per simulation. Kinetic::Kernel. The structure of a Kinetic::Kernel is analogous to the static CGAL (i.e., non-kinetic) kernels in that it defines a set of primitives and functors which generate certificates from the primitives. Kinetic::ActiveObjectsTable. Models of this concept hold a collection of kinetic primitives in a centralized manner. This structure centralizes management of the primitives in order to properly disseminate notifications when trajectories change, new primitives are added or primitives are deleted. There is generally one instance of a model of this concept per simulation. Kinetic::InstantaneousKernel. Models of this concept allow existing non-kinetic CGAL data structures to be used on a snapshot of kinetic data. As a result, pre-existing static structures can be used to initialize and audit kinetic data structures. Kinetic::FunctionKernel. This concept is the computational kernel of our framework. Models of this concept are responsible for representing, generating and manipulating the motional and certificate functions and their roots. It is this concept that provides the kinetic data structures framework with the necessary algebraic operations for manipulating event times. The Kinetic::FunctionKernel is discussed in detail in Section Algebraic Kernel. 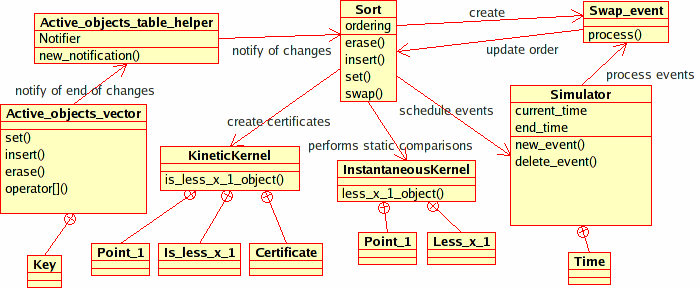
Kinetic::Sort<Traits, Visitor> kinetic data structure and the various pieces of our package. Other, more complicated, kinetic data structures will also use the Kinetic::InstantaneousKernel in order to insert/remove geometric primitives and audit themselves. Kinetic::Sort<Traits, Visitor> uses the sorting functionality in the STL instead. For simplicity, we added an additional concept, that of Kinetic::SimulationTraits, which wraps together a particular set of choices for the above concepts and is responsible for creating instances of each of the models. As a user of existing kinetic data structures, this is the only framework object you will have to create. The addition of this concept reduces the choices the user has to make to picking the dimension of the ambient space and choosing between exact and inexact computations. The model of Kinetic::SimulationTraits creates an instance each of the Kinetic::Simulator and Kinetic::ActiveObjectsTable. Handles for these instances as well as instances of the Kinetic::Kernel and Kinetic::InstantaneousKernel can be requested from the simulation traits class. Both the Kinetic::Kernel and the Kinetic::Simulator use the Kinetic::FunctionKernel, the former to find certificate failure times and the later to operate on them. For technical reasons, each supplied model of Kinetic::SimulationTraits also picks out a particular type of kinetic primitive which will be used by the kinetic data structures.
There are five provided kinetic data structures. They are
Kinetic::Sort<Traits, Visitor> maintain a list of pointssorted by x-coordinate.Kinetic::Delaunay_triangulation_2<Traits, Visitor, Triangulation> maintain the Delaunay triangulation of a set of two dimensional points.Kinetic::Delaunay_triangulation_3<Traits,Visitor, Triangulation> maintain the Delaunay triangulation of a set of three dimensional points.Kinetic::Regular_triangulation_3<Traits, Visitor, Triangulation> maintain the regular triangulation of a set of waiting three dimensional points.Kinetic::Enclosing_box_2<Traits> and Kinetic::Enclosing_box_3<Traits> restrict points to stay within a box by bouncing them off the walls.Using a kinetic data structure can be as simple as the following:
File Kinetic_data_structures/Kinetic_sort.cpp
Using the other kinetic data structures is substantially identical. Please see the appropriate files in the demo/Kinetic_data_structures directory.
In the example, first the Kinetic::SimulationTraits object is chosen (in this case one that supports exact computations). Then the kinetic data structure is defined using the chosen traits object and a visitor class which logs changes to the sorted list. Next, instances of the two are created and a set of points is read from a file. Then, the simulator is instructed to process all the events until the end of the simulation. Finally, a record of what happened is printed to the terminal.
Several important things happen behind the scenes in this example. First, the Kinetic::ActiveObjectsTable which holds the moving points notifies the kinetic data structure that new points have been added to the simulation. Second, the Kinetic::Sort<Traits,Visitor> kinetic data structure registers its events with the Kinetic::Simulator by providing a time and a proxy object for each event. When a particular event occurs, the Kinetic::Simulator calls a function on the proxy object which in turn updates the kinetic data structure.
The example illustrates how to monitor the supplied data structures as they evolve by using a Kinetic::SortVisitor object - a small class whose methods are called whenever the kinetic data structure changes. Hooks for such visitor concepts are provided for all of the shipped kinetic data structures. In the case of kinetic sorting, the visitor's methods are called every time a new point is inserted in the sorted list, when one is removed, or when two points are swapped in the sorted order.
The visitor concept is quite powerful, allowing us, for example, to implement a data structure for computing and storing two-dimensional arrangements of \( x\)-monotone curves on top of the Kinetic::Sort<Traits, Visitor> data structure using about 60 lines of code. This sweepline code is presented in Section Extending Kinetic Data Structures.
One key part of the framework not shown is how to create kinetic primitives (rather than just reading them in from a file). There are two ways to construction the necessary motion functions (which are models of Kinetic::FunctionKernel::Function). The first is to create an array of polynomial coeffients and simply call the constructor as in:
A slightly more flexible way is to use a Kinetic::FunctionKernel::ConstructFunction object. To do this do the following:
The Kinetic::FunctionKernel::ConstructFunction can be passed (almost) an number of arguments and will construct a polynomial with those arguments are coefficients.
Once the motion functions are constructed, constructing the primitive is just like constructing the corresponding static object.
The framework includes Qt widgets for displaying kinetic data structures in two and three dimensions. The following example shows using the two dimensional widget with a Delaunay triangulation:
The example shows how to use a number of additional features of the framework. First, it shows that two kinetic data structures (Kinetic::Delaunay_triangulation_2<Traits, Triangulation> and Kinetic::Enclosing_box_2<Traits>) can coexist on the same set of points without any extra effort. Both interact with the moving points through the active objects table, and never need to directly interact with one another. Second, objects (like qt_w, qt_mps and qt_dt2) are all stored by using reference counted handles (Object::Handle). This allows them to share references to one another without the user having to worry about memory management and order of deletion. For example, the Kinetic::Qt_triangulation_2<KineticDelaunay_2, QtWidget_2, Qt_moving_points_2> object needs a handle to the kinetic triangulation, in order to get the structure to display, and a handle to the Active_points_1_table to get the coordinates of the points.
Finally, the example shows how to use the graphical interface elements provided, see Figure 83.3. Our package includes Qt widgets for displaying kinetic geometry in two and three dimensions. In addition to being able to play and pause the simulation, the user can step through events one at a time and reverse the simulation to retrace what had happened. The three-dimensional visualization support is based on the Coin library http://www.coin3d.org.

| 
| 
| 
| 
|

| 
| 
| 
|
demo/Kinetic_data_structures/Kinetic_Delaunay_triangulation_2.cpp 
Qt_widget and adds buttons to play, pause, step through and run the simulation backwards. Here we present a simple example that uses the Kinetic::Sort<Traits, Visitor> kinetic data structure to compute an arrangement of algebraic functions. It wraps the sorting data structure and uses a visitor to monitor changes and map them to corresponding features in the arrangement. To see an example using this kinetic data structure read the example at examples/Kinetic_data_structures/Kinetic_sweepline.cpp.
First we define the visitor class. An object of this type is passed to the Kinetic::Sort<Traits, Visitor> data structure and turns events into calls on the arrangement structure. This class has to be defined externally since the arrangement will inherit from the sorting structure.
Now we define the actual arrangement data structure.
Finally, we have to set everything up. To do this we use some special event classes: Kinetic::Insert_event<ActiveObjectsTable> and Kinetic::Erase_event<ActiveObjectsTable>. These are events which can be put in the event queue which either insert a primitive into the set of active objects or remove it. Using these, we can allow curves in the arrangement to begin or end in arbitrary places.