8.1 Which Programs can be Solved?
This package lets you solve convex quadratic programs of the general form
|
- A is an m × n matrix (the constraint matrix),
- b is an m-dimensional vector (the right-hand side),
- ⋛ is an m-dimensional vector of relations from { ≤ , =, ≥ },
- l is an n-dimensional vector of lower bounds for x, where lj ∈ ℝ ∪ {-∞} for all j
- u is an n-dimensional vector of upper bounds for x, where uj ∈ ℝ ∪ {∞} for all j
- D is a symmetric positive-semidefinite n × n matrix (the quadratic objective function),
- c is an n-dimensional vector (the linear objective function), and
- c0 is a constant.
If D=0, the program (QP) is actually a linear program. Section 8.2.2 on robustness briefly discusses the case of D not being positive-semidefinite and therefore not defining a convex program.
Solving the program means to find an n-vector x* such that Ax* ⋛ b, l ≤ x* ≤ u (a feasible solution), and with the smallest objective function value x*TDx*+cTx*+c0 among all feasible solutions.
There might be no feasible solution at all, in which case the quadratic program is infeasible, or there might be feasible solutions of arbitrarily small objective function value, in which case the program is unbounded.
8.2 Design, Efficiency, and Robustness
The design of the package is quite simple. The linear or quadratic program to be solved is supplied in form of an object of a class that is a model of the concept QuadraticProgram (or some specialized other concepts, e.g. for linear programs). Cgal provides a number of easy-to-use and flexible models, see Section 8.3 below. The input data may be of any given number type, such as double, int, or any exact type.Then the program is solved using the function solve_quadratic_program (or some specialized other functions, e.g. for linear programs). For this, you also have to provide a suitable exact number type ET used in the solution process. In case of input type double, solution methods that use floating-point-filtering are chosen by default for certain programs (in some cases, this is not appropriate, and the default should be changed; see Section 8.8 for details).
The output of this is an object of Quadratic_program_solution<ET> which you can in turn query for various things: what is the status of the program (optimally solved, infeasible, or unbounded?), what are the values of the optimal solution x*, what is the associated objective function value, etc.
You can in particular get certificates for the solution. In short, these are proofs that the output is correct. Thus, if you don't believe in the solution (whether it says ``optimally solved'', ``infeasible'', or ``unbounded''), you can verify it yourself by using the certificates. Section 8.7 says more about this.
8.2.1 Efficiency
The concept QuadraticProgram (as well as the other specialized ones) require a dense interface of the program, in terms of random-access iterators over the matrices and vectors of (QP). Zero entries therefore play no special role and are treated like all other entries by the interface.This has mainly historical reasons: the original motivation behind this package was low-dimensional geometric optimization where a dense representation is appropriate and efficient. In fact, the Cgal packages Min_annulus_d<Traits> and Polytope_distance_d<Traits> internally use the linear and quadratic programming solver.
As a user, however, you don't necessarily have to provide a dense representation of your program. You do not pass vectors or matrices to the solution functions, but rather specify the vectors and matrices through iterators. The iterator abstraction easily allows to build models that convert a sparse representation into a dense interface. The predefined models Quadratic_program<NT> and Quadratic_program_from_mps<NT> do exactly this; in using them, you can forget about the dense interface.
Nevertheless, if you care about efficiency, you cannot completely ignore the issue. If you think about a quadratic program in n variables and m constraints, its dense interface has Θ(n2 + mn) entries, even if actually very few of them are nonzero. This has consequences for the complexity of the internal computations. In fact, a single iteration of the solution process has complexity at least Ω(mn), since usually, all entries of the matrix A are accessed. This implies that problems where min (n,m) is large cannot be solved efficiently, even if the number of nonzero entries in the problem description is very small.
We can actually be quite precise about performance, in terms of the following parameters.
| n | : | the number of variables (or columns of A), |
| m | : | the number of constraints (or rows of A), |
| e | : | the number of equality constraints, |
| r | : | the rank of the quadratic objective function matrix D. |
The time required to solve the problems is in most cases linear in max (n,m), but with a factor heavily depending on min (n,e)+r. Therefore, the solver will be efficient only if min (n,e)+r is small.
Here are the scenarios in which this applies:
- Quadratic programs with a small number of variables, but possibly a large number of inequality constraints,
- Linear programs with a small number of equality constraints but possibly a large number of variables,
- Quadratic programs with a small number of equality constraints and D of small rank, but possibly with a large number of variables.
How small is small? If min (n,e)+r is up to 10, the solver will probably be very fast, even if max (n,m) goes into the millions. If min (n,m)+r is up to a few hundreds, you may still get a solution within reasonable time, depending on the problem characteristics.
If you have a problem where both n and e are well above 1,000, say, then chances are high that Cgal cannot solve it within reasonable time.
8.2.2 Robustness
Given that you use an exact number type in the function solve_quadratic_program (or in the other, specialized solution functions), the solver will give you exact rational output, for every convex quadratic program. It may fail to compute a solution only if- The quadratic program is too large (see the previous subsection on efficiency).
- The quadratic objective function matrix D is not positive-semidefinite (see the discussion below).
- The floating-point filter used by default for certain programs and input type double fails due to a double exponent overflow. This happens in rare cases only, and it does not pay off to sacrifice the efficiency of the filtered approach in order to cope with these rare cases. There are means, however, to avoid such problems by switching to a slower non-filtered variant, see Section 8.8.1.
- The solver internally cycles. This also happens in rare cases only. However, if you have a hunch that the solver cycles on your problem, there are means to switch to a slower variant that is guaranteed not to cycle, see Section 8.8.2.
The second item merits special attention. First, you may ask why the solver does not check that D is positive semidefinite. But recall that D is given by a dense interface, and it would therefore cost Ω(n2) time already to access all entries of the matrix D. The solver itself gets away with accessing much less entries of D in the relevant case where r, the rank of D, is small.
Nevertheless, the solver contains some runtime checks that may detect that the matrix D is not positive-semidefinite. But you may as well get an ``optimal solution'' in this case, even with valid certificates. The validity of these certificates, however, depends on D being positive-semidefinite; if this is not the case, the certificates only prove that the solver has found a ``critical point'' of your (nonconvex) program, but there are no guarantees whatsoever that this is a global optimum, or even a local optimum.
8.3 How to Enter and Solve a Program
In this section, we describe how you can supply and solve your problem, using the Cgal program models and solution functions. There are two essentially different ways to proceed, and we will discuss them in turn. In short,- you can let the model take care of your program data; you start from an empty program and then simply insert the non-zero entries, or read them from a file (more generally, any input stream) in MPSFormat. You can also change program entries at any time. This is usually the most convenient way if you don't want to care about representation issues;
- you can maintain the data yourself and only supply suitable random-access iterators over the matrices and vectors. This is advantageous if you already have the data (explicitly, or implicitly encoded, for example through iterators) and want to avoid copying of data. Typically, this happens if you write generic iterator-based code.
Our running example is the following quadratic program in two variables:
|
Figure 8.1 shows a picture. It depicts the five inequalities of the program, along with the feasible region (green), the set of points that satisfy all the five constraints. The dashed elliptic curves represent contour lines of the objective function, i.e., along each dashed curve, the objective function value is constant.
The global minimum of the objective function is attained at the point (0,4), and the minimum within the feasible region appears at the point (2,3) marked with a black dot. The value of the objective function at this optimal solution is 22 + 4(3-4)2 = 8.
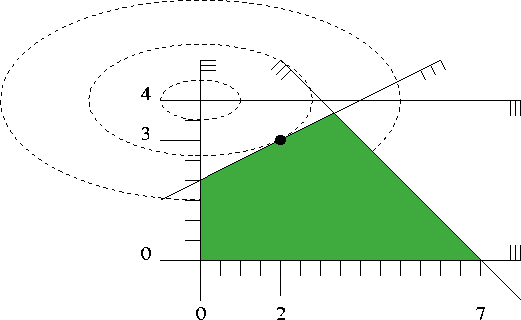
Figure 8.1: A quadratic program in two variables
8.3.1 Constructing a Program from Data
Here is how this quadratic program can be solved in Cgal according to the first way (letting the model take care of the data). We use int as the input type, and MP_Float or Gmpz (which is faster and preferable if GMP is installed) as the exact type for the internal computations. In larger examples, it pays off to use double as input type in order to profit from the automatic floating-point filtering that takes place then.For examples how to work with the input type double, we refer to Sections 8.5 and 8.8.
Note: For the quadratic objective function, the entries of the matrix 2D have to be provided, rather than D. Although this is common to almost all quadratic programming solvers, it can easily be overlooked by a novice.
File: examples/QP_solver/first_qp.cpp
#include <iostream>
#include <cassert>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
// program and solution types
typedef CGAL::Quadratic_program<int> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;
int main() {
// by default, we have a nonnegative QP with Ax <= b
Program qp (CGAL::SMALLER, true, 0, false, 0);
// now set the non-default entries:
const int X = 0;
const int Y = 1;
qp.set_a(X, 0, 1); qp.set_a(Y, 0, 1); qp.set_b(0, 7); // x + y <= 7
qp.set_a(X, 1, -1); qp.set_a(Y, 1, 2); qp.set_b(1, 4); // -x + 2y <= 4
qp.set_u(Y, true, 4); // y <= 4
qp.set_d(X, X, 2); qp.set_d (Y, Y, 8); // !!specify 2D!! x^2 + 4 y^2
qp.set_c(Y, -32); // -32y
qp.set_c0(64); // +64
// solve the program, using ET as the exact type
Solution s = CGAL::solve_quadratic_program(qp, ET());
assert (s.solves_quadratic_program(qp));
// output solution
std::cout << s;
return 0;
}
Asuming that GMP is installed, the output of the of the above program is:
status: OPTIMAL objective value: 8/1 variable values: 0: 2/1 1: 3/1If GMP is not installed, the values are of course the same, but numerator and denominator might have a common divisor that is not factored out.
8.3.2 Constructing a Program from a Stream
Here, the program data must be available in MPSFormat (the MPSFormat page shows how our running example looks like in this format, and it briefly explains the format). Assuming that your working directory contains the file first_qp.mps, the following program will read and solve it, with the same output as before.
File: examples/QP_solver/first_qp_from_mps.cpp
#include <iostream>
#include <fstream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
// program and solution types
typedef CGAL::Quadratic_program_from_mps<int> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;
int main() {
std::ifstream in ("first_qp.mps");
Program qp(in); // read program from file
assert (qp.is_valid()); // we should have a valid mps file
// solve the program, using ET as the exact type
Solution s = CGAL::solve_quadratic_program(qp, ET());
// output solution
std::cout << s;
return 0;
}
8.3.3 Constructing a Program from Iterators
The following program again solves our running example from above, with the same output, but this time with iterators over data stored in suitable containers. You can see that we also store zero entries here (in D). For this toy problem, the previous two approaches (program from data/stream) are clearly preferable, but Section 8.5 shows an example where it makes sense to use the iterator-based approach.
File: examples/QP_solver/first_qp_from_iterators.cpp
#include <iostream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
// program and solution types
typedef CGAL::Quadratic_program_from_iterators
<int**, // for A
int*, // for b
CGAL::Const_oneset_iterator<CGAL::Comparison_result>, // for r
bool*, // for fl
int*, // for l
bool*, // for fu
int*, // for u
int**, // for D
int*> // for c
Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;
int main() {
int Ax[] = {1, -1}; // column for x
int Ay[] = {1, 2}; // column for y
int* A[] = {Ax, Ay}; // A comes columnwise
int b[] = {7, 4}; // right-hand side
CGAL::Const_oneset_iterator<CGAL::Comparison_result>
r( CGAL::SMALLER); // constraints are "<="
bool fl[] = {true, true}; // both x, y are lower-bounded
int l[] = {0, 0};
bool fu[] = {false, true}; // only y is upper-bounded
int u[] = {0, 4}; // x's u-entry is ignored
int D1[] = {2}; // 2D_{1,1}
int D2[] = {0, 8}; // 2D_{2,1}, 2D_{2,2}
int* D[] = {D1, D2}; // D-entries on/below diagonal
int c[] = {0, -32};
int c0 = 64; // constant term
// now construct the quadratic program; the first two parameters are
// the number of variables and the number of constraints (rows of A)
Program qp (2, 2, A, b, r, fl, l, fu, u, D, c, c0);
// solve the program, using ET as the exact type
Solution s = CGAL::solve_quadratic_program(qp, ET());
// output solution
std::cout << s;
return 0;
}
Note 1: The example shows an interesting feature of this approach: not all data need to come from containers. Here, the iterator over the vector of relations can be provided through the class Const_oneset_iterator<T>, since all entries of this vector are equal to CGAL::SMALLER. The same could have been done with the vector fl for the finiteness of the lower bounds.
Note 2: The program type looks a bit scary, with its total of 9 template arguments, one for each iterator type. In Section 8.5.1 we show how the explicit construction of this type can be circumvented.
8.4 Solving Linear and Nonnegative Programs
Let us reconsider the general form of (QP) from Section 8.1 above. If D=0, the quadratic program is in fact a linear program, and in the case that the bound vectors l is the zero vector and all entries of u are ∞, the program is said to be nonnegative. The package offers dedicated models and solution methods for these special cases.From an interface perspective, this is just syntactic sugar: in the model Quadratic_program<NT>, we can easily set the default bounds so that a nonnegative program results, and a linear program is obtained by simply not inserting any D-entries. Even in the iterator-based approach (see QP_solver/first_qp_from_iterators.cpp), linear and nonnegative programs can easily be defined through suitable Const_oneset_iterator<T>-style iterators.
The main reason for having dedicated solution methods for linear and nonnegative programs is efficiency: if the solver knows that the program is linear, it can save some computations compared to the general solver that unknowingly has to fiddle around with a zero D-matrix. As in Section 8.2.2 above, we can argue that checking in advance whether D=0 is not an option in general, since this may require Ω(n2) time on the dense interface.
Similarly, if the solver knows that the program is nonnegative, it will be more efficient than under the general bounds l ≤ x ≤ u. You can argue that nonnegativity is something that could easily be checked in time O(n) beforehand, but then again nonnegative programs are so frequent that the syntactic sugar aspect becomes somewhat important. After all, we can save four iterators in specifying a nonnegative linear program in terms of the concept NonnegativeLinearProgram rather than LinearProgram.
Often, there are no bounds at all for the variables, i.e., all entries of l are -∞, and all entries of u are ∞ (this is called a free program). There is no dedicated solution method for this case (a free quadratic or linear program is treated like a general quadratic or linear program), but all predefined models make it easy to specify all sorts of default bounds, covering the free case.
8.4.1 The Linear Programming Solver
Let's go back to our first quadratic program from above and change it into a linear program by simply removing the quadratic part of the objective function:
|
Figure 8.2 shows how this looks like. We will not visualize a linear objective function with contour lines but with arrows instead. The arrow represents the (direction) of the vector -c, and we are looking for a feasible solution that is ``extreme'' in the direction of the arrow. In our small example, this is the unique point ``on'' the two constraints x1+x2 ≤ 7 and -x1+x2 ≤ 4, the point (10/3,11/3) marked with a black dot. The optimal objective function value is -32(11/3)+64=-160/3.
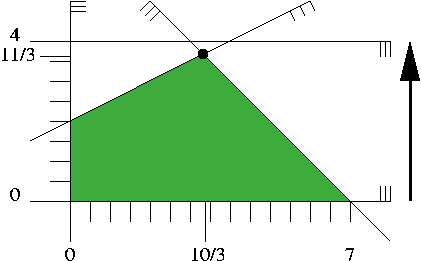
Figure 8.2: A linear program in two variables
Here is Cgal code for solving it, using the dedicated LP solver, and according to the three ways for constructing a program that we have already discussed in Section 8.3.
QP_solver/first_lp.cpp
QP_solver/first_lp_from_mps.cpp
QP_solver/first_lp_from_iterators.cpp
In all cases, the output is
status: OPTIMAL objective value: -160/3 variable values: 0: 10/3 1: 11/3
8.4.2 The Nonnegative Quadratic Programming Solver
If we go back to our first quadratic program and remove the constraint y ≤ 4, we arrive at a nonnegative quadratic program:
|
Figure 8.3 contains the illustration; since the constraint y ≤ 4 was redundant, the feasible region and the optimal solution do not change.
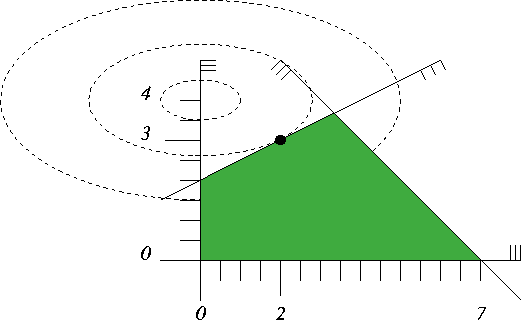
Figure 8.3: A nonnegative quadratic program in two variables
The following programs (using the dedicated solver for nonnegative quadratic programs) will therefore again output
status: OPTIMAL objective value: 8/1 variable values: 0: 2/1 1: 3/1
QP_solver/first_nonnegative_qp.cpp
QP_solver/first_nonnegative_qp_from_mps.cpp
QP_solver/first_nonnegative_qp_from_iterators.cpp
8.4.3 The Nonnegative Linear Programming Solver
Finally, a dedicated model and function is available for nonnnegative linear programs as well. Let's take our linear program from above and remove the constraint y ≤ 4 to obtain a nonnegative linear program. At the same time we remove the constant objective function term to get a ``minimal'' input and a ``shortest'' program; the optimal value is -32(11/3)=-352/3.
|
This can be solved by any of the following three programs
QP_solver/first_nonnegative_lp.cpp
QP_solver/first_nonnegative_lp_from_mps.cpp
QP_solver/first_nonnegative_lp_from_iterators.cpp
The output will always be
status: OPTIMAL objective value: -352/3 variable values: 0: 10/3 1: 11/3
8.5 Working from Iterators
Here we present a somewhat more advanced example that emphasizes the usefulness of solving linear and quadratic programs from iterators. Let's look at a situation in which a linear program is given implicitly, and access to it is gained through properly constructed iterators.The problem we are going to solve is the following: given points p1, … pn in d-dimensional space and another point p: is p in the convex hull of {p1, … ,pn}? In formulas, this is the case if and only if there are real coefficients λ1, … ,λn such that p is a convex combination of p1, … ,pn:
| p = |
| , |
| = 1, λj ≥ 0 for all j. |
| qj = hj ⋅ (pj | 1) for all j, and q = h ⋅ (p | 1). |
| = (p | 1), |
| = q, µj ≥ 0 for all j. |
The linear program now tests for the existence of nonnegative µj that satisfy the latter equation. Below is the code; it defines a function that solves the linear program, given p and p1, … ,pn (through an iterator range). The only (mild) trickery involved is the construction of the nested iterator through a fixed column of the constraint matrix A. We get this from transforming the iterator through the points using a functor that maps a point to an iterator through its homogeneous coordinates.
File: examples/QP_solver/solve_convex_hull_containment_lp.h
#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin {
typedef typename Point_d::Homogeneous_const_iterator result_type;
result_type operator() (const Point_d& p) const {
return p.homogeneous_begin();
}
};
// function to solve the LP that tests whether a point is in the
// convex hull of other points; the type ET is an exact type used
// for the internal computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
RandomAccessIterator begin,
RandomAccessIterator end, const ET& dummy)
{
// Constraint matrix type: A[j][i] is the i-th homogeneous coordinate of p_j
typedef boost::transform_iterator
<Homogeneous_begin<Point_d>, RandomAccessIterator> A_it;
// Right-hand side type: b[i] is the i-th homogeneous coordinate of p
typedef typename Point_d::Homogeneous_const_iterator B_it;
// Relation type ("=")
typedef CGAL::Const_oneset_iterator<CGAL::Comparison_result> R_it;
// input number type
typedef typename CGAL::Kernel_traits<Point_d>::Kernel::RT RT;
// Linear objective function type (c=0: we only test feasibility)
typedef CGAL::Const_oneset_iterator<RT> C_it;
// the nonnegative linear program type
typedef
CGAL::Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it>
Program;
// ok, we are prepared now: construct program and solve it
Program lp (end-begin, // number of variables
p.dimension()+1, // number of constraints
A_it (begin), B_it (p.homogeneous_begin()),
R_it (CGAL::EQUAL), C_it (0));
return CGAL::solve_nonnegative_linear_program (lp, dummy);
}
To see this in action, let us call it with p1=(0,0), p2=(10,0), p3=(0,10) fixed (they define a triangle) and all integral points p in [0,10]2. We know that p is in the convex hull of {p1,p2,p3} if and only if its two coordinates sum up to 10 at most. As the exact type, we use MP_Float or Gmpzf (which is faster and preferable if GMP is installed).
File: examples/QP_solver/convex_hull_containment.cpp
#include <cassert>
#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include "solve_convex_hull_containment_lp.h"
// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;
bool is_in_convex_hull (const Point_d& p,
std::vector<Point_d>::const_iterator begin,
std::vector<Point_d>::const_iterator end)
{
CGAL::Quadratic_program_solution<ET> s =
solve_convex_hull_containment_lp (p, begin, end, ET(0));
return !s.is_infeasible();
}
int main()
{
std::vector<Point_d> points;
// convex hull: simplex spanned by {(0,0), (10,0), (0,10)}
points.push_back (Point_d ( 0.0, 0.0));
points.push_back (Point_d (10.0, 0.0));
points.push_back (Point_d ( 0.0, 10.0));
for (int i=0; i<=10; ++i)
for (int j=0; j<=10; ++j) {
// (i,j) is in the simplex iff i+j <= 10
bool contained = is_in_convex_hull
(Point_d (i, j), points.begin(), points.end());
assert (contained == (i+j<=10));
}
return 0;
}
8.5.1 Using Makers
You already noticed in the previous example that the actual template arguments for CGAL::Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it> can be quite elaborate, and this only gets worse if you plug more iterators into each other. In general, you want to construct a program from given expressions for the iterators, but the types of these expressions are probably very complicated and difficult to look up.You can avoid the explicit construction of the type CGAL::Nonnegative_linear_program_from_iterators<A_it, B_it, R_it, C_it> if you only need an expression of it, e.g. to pass it directly as an argument to the solving function. Here is an alternative version of QP_solver/solve_convex_hull_containment_lp.h that shows how this works. In effect, you get shorter and more readable code.
File: examples/QP_solver/solve_convex_hull_containment_lp2.h
#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin {
typedef typename Point_d::Homogeneous_const_iterator result_type;
result_type operator() (const Point_d& p) const {
return p.homogeneous_begin();
}
};
// function to test whether point is in the convex hull of other points;
// the type ET is an exact type used for the computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
RandomAccessIterator begin,
RandomAccessIterator end, const ET& dummy)
{
// construct program and solve it
return CGAL::solve_nonnegative_linear_program
(CGAL::make_nonnegative_linear_program_from_iterators
(end-begin, // n
p.dimension()+1, // m
boost::transform_iterator
<Homogeneous_begin<Point_d>, RandomAccessIterator>(begin), // A
typename Point_d::Homogeneous_const_iterator (p.homogeneous_begin()),// b
CGAL::Const_oneset_iterator<CGAL::Comparison_result>(CGAL::EQUAL), // ~
CGAL::Const_oneset_iterator
<typename CGAL::Kernel_traits<Point_d>::Kernel::RT> (0)), dummy); // c
}
8.6 Important Variables and Constraints
If you have a solution x* of a linear or quadratic program, the ``important'' variables are typically the ones that are not on their bounds. In case of a nonnegative program, these are the nonzero variables. Going back to the example of the previous Section 8.5, we can easily interpret their importance: the nonzero variables correspond to points pj that actually contribute to the convex combination that yields p.The following example shows how we can access the important variables, using the iterators basic_variable_indices_begin() and basic_variable_indices_end().
We generate a set of points that form a 4-gon in [0,4]2, and then find the ones that contribute to the convex combinations of all 25 lattice points in [0,4]2. If the lattice point in question is not in the 4-gon, we simply output this fact.
File: examples/QP_solver/important_variables.cpp
#include <cassert>
#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include "solve_convex_hull_containment_lp2.h"
typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;
typedef CGAL::Quadratic_program_solution<CGAL::MP_Float> Solution;
int main()
{
std::vector<Point_d> points;
// convex hull: 4-gon spanned by {(1,0), (4,1), (4,4), (2,3)}
points.push_back (Point_d (1, 0)); // point 0
points.push_back (Point_d (4, 1)); // point 1
points.push_back (Point_d (4, 4)); // point 2
points.push_back (Point_d (2, 3)); // point 3
// test all 25 integer points in [0,4]^2
for (int i=0; i<=4; ++i)
for (int j=0; j<=4; ++j) {
Point_d p (i, j);
Solution s = solve_convex_hull_containment_lp
(p, points.begin(), points.end(), CGAL::MP_Float());
std::cout << p;
if (s.is_infeasible())
std::cout << " is not in the convex hull\n";
else {
assert (s.is_optimal());
std::cout << " is a convex combination of the points ";
Solution::Index_iterator it = s.basic_variable_indices_begin();
Solution::Index_iterator end = s.basic_variable_indices_end();
for (; it != end; ++it) std::cout << *it << " ";
std::cout << std::endl;
}
}
return 0;
}
It turns out that exactly three of the four points contribute to any convex combination, even through there are lattice points that lie in the convex hull of less than three of the points. This shows that the set of basic variables that we access in the example does not necessarily coincide with the set of important variables as defined above. In fact, it is only guaranteed that a non-basic variable attains one of its bounds, but there might be basic variables that also have this property. In linear and quadratic programming terms, such a situation is called a degeneracy.
There is also the concept of an important constraint: this is typically a constraint in the system Ax ⋛ b that is satisfied with equality at x*. Program QP_solver/first_qp_basic_constraints.cpp shows how these can be accessed, using the iterators basic_constraint_indices_begin() and basic_constraint_indices_end().
Again, we have a disagreement between ``basic'' and ``important'': it is guaranteed that all basic constraints are satisfied with equality at x*, but there might be non-basic constraints that are satisfied with equality as well.
8.7 Solution Certificates
Suppose the solver tells you that the problem you have entered is infeasible. Why should you believe this? Similarly, you can quite easily verify that a claimed optimal solution is feasible, but why is there no better one?Certificates are proofs that the solver can give you in order to convince you that what it claims is indeed true. The archetype of such a proof is Farkas Lemma [MG06].
Farkas Lemma: Either the inequality system
|
|
Thus, if someone wants to convince you that the first system in the Farkas Lemma is infeasible, that person can simply give you a vector y that solves the second system. Since you can easily verify yourself that the y you got satisfies this second system, you now have a certificate for the infeasibility of the first system, assuming that you believe in Farkas Lemma.
Here we show how the solver can convince you. We first set up an infeasible linear program with constraints of the type Ax ≤ b, x ≥ 0; then we solve it and ask for a certificate. Finally, we verify the certificate by simply checking the inequalities of the second system in Farkas Lemma.
File: examples/QP_solver/infeasibility_certificate.cpp
#include <cassert>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// choose exact integral type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
// program and solution types
typedef CGAL::Nonnegative_linear_program_from_iterators
<int**, // for A
int*, // for b
CGAL::Comparison_result*, // for r
int*> // for c
Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;
// we demonstrate Farkas Lemma: either the system
// A x <= b
// x >= 0
// has a solution, or there exists y such that
// y >= 0
// y^TA >= 0
// y^Tb < 0
// In the following instance, the first system has no solution,
// since adding up the two inequalities gives x_2 <= -1:
// x_1 - 2x_2 <= 1
// -x_1 + 3x_2 <= -2
// x_1, x_2 >= 0
int main() {
int Ax1[] = { 1, -1}; // column for x1
int Ax2[] = {-2, 3}; // column for x2
int* A[] = {Ax1, Ax2}; // A comes columnwise
int b[] = {1, -2}; // right-hand side
CGAL::Comparison_result
r[] = {CGAL::SMALLER, CGAL::SMALLER}; // constraints are "<="
int c[] = {0, 0}; // zero objective function
// now construct the linear program; the first two parameters are
// the number of variables and the number of constraints (rows of A)
Program lp (2, 2, A, b, r, c);
// solve the program, using ET as the exact type
Solution s = CGAL::solve_nonnegative_linear_program(lp, ET());
// get certificate for infeasibility
assert (s.is_infeasible());
Solution::Infeasibility_certificate_iterator y =
s.infeasibility_certificate_begin();
// check y >= 0
assert (y[0] >= 0);
assert (y[1] >= 0);
// check y^T A >= 0
assert (y[0] * A[0][0] + y[1] * A[0][1] >= 0);
assert (y[0] * A[1][0] + y[1] * A[1][1] >= 0);
// check y^T b < 0
assert (y[0] * b[0] + y[1] * b[1] < 0);
return 0;
}
There are similar certificates for optimality and unboundedness that you can see in action in the programs QP_solver/optimality_certificate.cpp and QP_solver/unboundedness_certificate.cpp. The underlying variants of Farkas Lemma are somewhat more complicated, due to the mixed relations in ⋛ and the general bounds. The certificate section of Quadratic_program_solution<ET> gives the full picture and mathematically proves the correctness of the certificates.
8.8 Customizing the Solver
Sometimes it is necessary to alter the default behavior of the solver. This can be done by passing a suitably prepared object of the class Quadratic_program_options to the solution functions. Most options concern ``soft'' issues like verbosity, but there are two notable case where it is of critical importance to be able to change the defaults.8.8.1 Exponent Overflow in Double Using Floating-Point Filters
The filtered version of the solver that is used for some problems by default on input type double internally constructs double-approximations of exact multiprecision values. If these exact values are extremely large, this may lead to infinite double values and incorrect results. In debug mode, the solver will notice this through a certificate cross-check in the end (or even earlier). In this case, it is advisable to explicitly switch to a non-filtered pricing strategy, see Quadratic_program_pricing_strategy.Hint: If you have a program where the number of variables n and the number of constraints m have the same order of magnitude, the filtering will usually have no dramatic effect on the performance, so in that case you might as well switch to QP_PARTIAL_DANTZIG to be safe from the issue described here (see QP_solver/cycling.cpp for an example that shows how to change the pricing strategy).
8.8.2 The Solver Internally Cycles
Consider the following program. It reads a nonnegative linear program from the file cycling.mps (which is in the example directory as well), and then solves it in verbose mode, using Bland's rule, see Quadratic_program_pricing_strategy.
File: examples/QP_solver/cycling.cpp
#include <iostream>
#include <fstream>
#include <CGAL/basic.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
// program and solution types
typedef CGAL::Quadratic_program_from_mps<double> Program;
typedef CGAL::Quadratic_program_solution<ET> Solution;
int main() {
std::ifstream in ("cycling.mps");
Program lp(in); // read program from file
assert (lp.is_valid()); // we should have a valid mps file...
assert (lp.is_linear()); // ... and it should be linear...
assert (lp.is_nonnegative()); // as well as nonnegative
// solve the program, using ET as the exact type
// choose verbose mode and Bland pricing
CGAL::Quadratic_program_options options;
options.set_verbosity(1); // verbose mode
options.set_pricing_strategy(CGAL::QP_BLAND); // Bland's rule
options.set_auto_validation(true); // automatic self-check
Solution s = CGAL::solve_nonnegative_linear_program(lp, ET(), options);
assert (s.is_valid()); // did the self-check succeed?
// output solution
std::cout << s;
return 0;
}
If you comment the line
options.set_pricing_strategy(CGAL::QP_BLAND); // Bland's ruleyou will see that the solver cycles: the verbose mode outputs the same sequence of six iterations over and over again. By switching to QP_BLAND, the solution process typically slows down a bit (it may also speed up in some cases), but now it is guaranteed that no cycling occurs.
In general, the verbose mode can be of use when you are not sure whether the solver ``has died'', or whether it simply takes very long to solve your problem. We refer to the class Quadratic_program_options for further details.
8.9 Some Benchmarks for Convex Hull Containment
Here we want to show what you can expect from the solver's performance in a specific application; we don't know whether this application is typical in your case, and we make no claims whatsoever about the performance in other applications.Still, the example shows that the performance can be dramatically affected by switching between pricing strategies, and we give some hints on how to achieve good performance in general.
The application is the one already discussed in Section 8.5 above: testing whether a point is in the convex hull of other points. To be able to switch between pricing strategies, we add another parameter of type Quadratic_program_options to the function solve_convex_hull_containment_lp that we pass on to the solution function:
File: examples/QP_solver/solve_convex_hull_containment_lp3.h
#include <boost/config.hpp>
#include <boost/iterator/transform_iterator.hpp>
#include <CGAL/Kernel_traits.h>
#include <CGAL/QP_options.h>
#include <CGAL/QP_models.h>
#include <CGAL/QP_functions.h>
// unary function to get homogeneous begin-iterator of point
template <class Point_d>
struct Homogeneous_begin {
typedef typename Point_d::Homogeneous_const_iterator result_type;
result_type operator() (const Point_d& p) const {
return p.homogeneous_begin();
}
};
// function to test whether point is in the convex hull of other points;
// the type ET is an exact type used for the computations
template <class Point_d, class RandomAccessIterator, class ET>
CGAL::Quadratic_program_solution<ET>
solve_convex_hull_containment_lp (const Point_d& p,
RandomAccessIterator begin,
RandomAccessIterator end, const ET& dummy,
const CGAL::Quadratic_program_options& o)
{
// construct program and solve it
return CGAL::solve_nonnegative_linear_program
(CGAL::make_nonnegative_linear_program_from_iterators
(end-begin, // n
p.dimension()+1, // m
boost::transform_iterator
<Homogeneous_begin<Point_d>, RandomAccessIterator>(begin), // A
typename Point_d::Homogeneous_const_iterator (p.homogeneous_begin()),// b
CGAL::Const_oneset_iterator<CGAL::Comparison_result>(CGAL::EQUAL), // ~
CGAL::Const_oneset_iterator
<typename CGAL::Kernel_traits<Point_d>::Kernel::RT> (0)), // c
dummy, o);
}
Now let us test containment of the origin in the convex hull of n random points in [0,1]d (it will most likely not be contained, and it turns out that this is the most expensive case). In the program below, we use d=10 and n=100,000, and we comment on some other combinations of n and d below (feel free to experiment with still other values).
File: examples/QP_solver/convex_hull_containment_benchmarks.cpp
#include <vector>
#include <CGAL/Cartesian_d.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Random.h>
#include <CGAL/Timer.h>
#include "solve_convex_hull_containment_lp3.h"
// choose exact floating-point type
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpzf.h>
typedef CGAL::Gmpzf ET;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float ET;
#endif
typedef CGAL::Cartesian_d<double> Kernel_d;
typedef Kernel_d::Point_d Point_d;
int main()
{
const int d = 10; // change this in order to experiment
const int n = 100000; // change this in order to experiment
// generate n random d-dimensional points in [0,1]^d
CGAL::Random rd;
std::vector<Point_d> points;
for (int j =0; j<n; ++j) {
std::vector<double> coords;
for (int i=0; i<d; ++i)
coords.push_back(rd.get_double());
points.push_back (Point_d (d, coords.begin(), coords.end()));
}
// benchmark all pricing strategies in turn
CGAL::Quadratic_program_pricing_strategy strategy[] = {
CGAL::QP_CHOOSE_DEFAULT, // QP_PARTIAL_FILTERED_DANTZIG
CGAL::QP_DANTZIG, // Dantzig's pivot rule...
CGAL::QP_PARTIAL_DANTZIG, // ... with partial pricing
CGAL::QP_BLAND, // Bland's pivot rule
CGAL::QP_FILTERED_DANTZIG, // Dantzig's filtered pivot rule...
CGAL::QP_PARTIAL_FILTERED_DANTZIG // ... with partial pricing
};
CGAL::Timer t;
for (int i=0; i<6; ++i) {
// test strategy i
CGAL::Quadratic_program_options options;
options.set_pricing_strategy (strategy[i]);
t.reset(); t.start();
// is origin in convex hull of the points? (most likely, not)
solve_convex_hull_containment_lp
(Point_d (d, CGAL::ORIGIN), points.begin(), points.end(),
ET(0), options);
t.stop();
std::cout << "Time (s) = " << t.time() << std::endl;
}
return 0;
}
If you compile with the macros NDEBUG or CGAL_QP_NO_ASSERTIONS set (this is essential for good performance!!), you will see runtimes that qualitatively look as follows (on your machine, the actual runtimes will roughly be some fixed multiples of the numbers in the table below, and they might vary with the random choices). The default choice of the pricing strategy in that case is QP_PARTIAL_FILTERED_DANTZIG.
| strategy | runtime in seconds | |
| CGAL::QP_CHOOSE_DEFAULT | | | 0.32 |
| CGAL::QP_DANTZIG | | | 10.7 |
| CGAL::QP_PARTIAL_DANTZIG | | | 3.72 |
| CGAL::QP_BLAND | | | 3.65 |
| CGAL::QP_FILTERED_DANTZIG | | | 0.43 |
| CGAL::QP_PARTIAL_FILTERED_DANTZIG | | | 0.32 |
We clearly see the effect of filtering: we gain a factor of ten, roughly, compared to the next best non-filtered variant.
8.9.1 d=3, n=1,000,000
The filtering effect is amplified if the points/dimension ratio becomes larger. This is what you might see in dimension three, with one million points.
| strategy | runtime in seconds | |
| CGAL::QP_CHOOSE_DEFAULT | | | 1.34 |
| CGAL::QP_DANTZIG | | | 47.6 |
| CGAL::QP_PARTIAL_DANTZIG | | | 15.6 |
| CGAL::QP_BLAND | | | 16.02 |
| CGAL::QP_FILTERED_DANTZIG | | | 1.89 |
| CGAL::QP_PARTIAL_FILTERED_DANTZIG | | | 1.34 |
In general, if your problem has a high variable/constraint or constraint/variable ratio, then filtering will typically pay off. In such cases, it might be beneficial to encode your problem using input type double in order to profit from the filtering (but see the issue discussed in Section 8.8.1).
8.9.2 d=100, n=100,000
Conversely, the filtering effect deteriorates if the points/dimension ratio becomes smaller.
| strategy | runtime in seconds | |
| CGAL::QP_CHOOSE_DEFAULT | | | 3.05 |
| CGAL::QP_DANTZIG | | | 78.4 |
| CGAL::QP_PARTIAL_DANTZIG | | | 45.9 |
| CGAL::QP_BLAND | | | 33.2 |
| CGAL::QP_FILTERED_DANTZIG | | | 3.36 |
| CGAL::QP_PARTIAL_FILTERED_DANTZIG | | | 3.06 |
8.9.3 d=500, n=1,000
If the points/dimension ratio tends to a constant, filtering is no longer a clear winner. The reason is that in this case, the necessary exact calculations with multiprecision numbers dominate the overall runtime.
| strategy | runtime in seconds | |
| CGAL::QP_CHOOSE_DEFAULT | | | 2.65 |
| CGAL::QP_DANTZIG | | | 5.55 |
| CGAL::QP_PARTIAL_DANTZIG | | | 5.6 |
| CGAL::QP_BLAND | | | 4.46 |
| CGAL::QP_FILTERED_DANTZIG | | | 2.65 |
| CGAL::QP_PARTIAL_FILTERED_DANTZIG | | | 2.61 |
In general, if you have a program where the number of variables and the number of constraints have the same order of magnitude, then the saving gained from using the filtered approach is typically small. In such a situation, you should consider switching to a non-filtered variant in order to avoid the rare issue discussed in Section 8.8.1 altogether.