|
CGAL 6.1 - Intersecting Sequences of dD Iso-oriented Boxes
|
|
CGAL 6.1 - Intersecting Sequences of dD Iso-oriented Boxes
|
Simple questions on geometric primitives, such as intersection and distance computations, can themselves become quite expensive if the primitives are not so simple anymore, for example, three-dimensional triangles and facets of polyhedral surfaces. Thus algorithms operating on these primitives tend to be slow in practice. A common (heuristic) optimization approximates the geometric primitives with their axis-aligned bounding boxes, runs a suitable modification of the algorithm on the boxes, and whenever a pair of boxes has an interesting interaction Boxes represent volumes or point-sets. So, intersection means intersection of the point-set enclosed by the box and not only intersection of the boundary, of course., only then the exact answer is computed on the complicated geometric primitives contained in the boxes.
We provide an efficient algorithm [2] for finding all intersecting pairs for large numbers of iso-oriented boxes, i.e., typically these will be such bounding boxes of more complicated geometries. One immediate application of this algorithm is the detection of all intersections (and self-intersections) for polyhedral surfaces, i.e., applying the algorithm on a large set of triangles in space, we give an example program later in this chapter. Not so obvious applications are proximity queries and distance computations among such surfaces, see Section Example for Point Proximity Search with a Custom Traits Class for an example and [2] for more details.
A \( d\)-dimensional iso-oriented box is defined as the Cartesian product of \( d\) intervals. We call the box half-open if the \( d\) intervals \( \{ [lo_i,hi_i) \,|\, 0 \leq
i < d\}\) are half-open intervals, and we call the box closed if the \( d\) intervals \( \{ [lo_i,hi_i] \,|\, 0 \leq i < d\}\) are closed intervals. Note that closed boxes support zero-width boxes and they can intersect at their boundaries, while non-empty half-open boxes always have a positive volume and they only intersect iff their interiors overlap. The distinction between closed and half-open boxes does not require a different representation of boxes, just a different interpretation when comparing boxes, which is selected with the two possible values for the topology parameter:
The number type of the interval boundaries must be one of the built-in types int, unsigned int, double or float.
In addition, a box has a unique id-number. It is used to order boxes consistently in each dimension even if boxes have identical coordinates. In consequence, the algorithm guarantees that a pair of intersecting boxes is reported only once. Note that boxes with equal id-number are not reported since they obviously intersect trivially.
The box intersection algorithm comes in two flavors: One algorithm works on a single sequence of boxes and computes all pairwise intersections, which is called the complete case, and used, for example, in the self-intersection test. The other algorithm works on two sequences of boxes and computes the pairwise intersections between boxes from the first sequence with boxes from the second sequence, which is called the bipartite case. For each pairwise intersection found a callback function is called with two arguments; the first argument is a box from the first sequence and the second argument a box from the second sequence. In the complete case, the second argument is a box from an internal copy of the first sequence.
The box intersection algorithm is implemented as a family of generic functions; the functions for the complete case accept one iterator range, and the functions for the bipartite case accept two iterator ranges. The callback function for reporting the intersecting pairs is provided as a template parameter of the BinaryFunction concept. The two principle function calls utilizing all default arguments look as follows:
Additional parameters to the functions calls are a cutoff value to adjust performance trade-offs, and a topology parameter selecting between topologically closed boxes (the default) and topologically half-open boxes.
The algorithm reorders the boxes in the course of the algorithm. Now, depending on the size of a box it can be faster to copy the boxes, or to work with pointers to boxes and copy only pointers. We offer automatic support for both options. To simplify the description, let us call the value_type of the iterator ranges box handle. The box handle can either be our box type itself or a pointer (or const pointer) to the box type; these choices represent both options from above.
In general, the algorithms treat the box type as opaque type and just assume that they are models of the Assignable concept, so that the algorithms can modify the input sequences and reorder the boxes. The access to the box dimension and box coordinates is mediated with a traits class of the BoxIntersectionTraits_d concept. A default traits class is provided that assumes that the box type is a model of the BoxIntersectionBox_d concept and that the box handle, i.e., the iterators value type, is identical to the box type or a pointer to the box type (see the previous paragraph for the value versus pointer nature of the box handle).
Two implementations of iso-oriented boxes are provided; Box_intersection_d::Box_d as a plain box, and Box_intersection_d::Box_with_handle_d as a box plus a handle that can be used to point to the full geometry that is approximated by the box. Both implementations have template parameters for the number type used for the interval bounds, for the fixed dimension of the box, and for a policy class [1] selecting among several solutions for providing the id-number.
The function signatures for the bipartite case look as follows. The signatures for the complete case with the box_self_intersection_d() function look the same except for the single iterator range.
The box implementation provided with Box_intersection_d::Box_d<double,2> has a dedicated constructor for the CGAL bounding box type Bbox_2 (similar for dimension 3). We use this in our minimal example to create easily nine two-dimensional boxes in a grid layout of \( 3
\times 3\) boxes. Additionally we pick the center box and the box in the upper-right corner as our second box sequence query.
The default policy of the box type implements the id-number with an explicit counter in the boxes, which is the default choice since it always works, but it costs space that could potentially be avoided, see the example in the next section. We use the id-number in our callback function to report the result of the intersection algorithm. The result will be that the first query box intersects all nine boxes and the second query box intersects the four boxes in the upper-right quadrant. See Section Example Using the Topology and the Cutoff Parameters for the change of the topology parameter and its effect.
File Box_intersection_d/minimal.cpp
The conventional application of the axis-aligned box intersection algorithm will start from complex geometry, here 3D triangles, approximate them with their bounding box, compute the intersecting pairs of boxes, and check only for those if the original triangles intersect as well.
We start in the main function and create ten triangles with endpoints chosen randomly in a cube \( [-1,+1)^3\). We store the triangles in a vector called triangles.
Next we create a vector for the bounding boxes of the triangles called boxes. For the boxes we choose the type Box_with_handle_d<double,3,Iterator> that works nicely together with the CGAL bounding boxes of type Bbox_3. In addition, each box stores the iterator to the corresponding triangle.
The default policy of this box type uses for the id-number the address of the value of the iterator, i.e., the address of the triangle. This is a good choice that works correctly iff the boxes have unique iterators, i.e., there is a one-to-one mapping between boxes and approximated geometry, which is the case here. It saves us the extra space that was needed for the explicit id-number in the previous example.
We run the self intersection algorithm with the report_inters() function as callback. This callback reports the intersecting boxes. It uses the handle and the global triangles vector to calculate the triangle numbers. Then it checks the triangles themselves for intersection and reports if not only the boxes but also the triangles intersect. We take some precautions before the intersection test in order to avoid problems, although unlikely, with degenerate triangles that we might have created with the random process.
This example can be easily extended to test polyhedral surfaces of the Polyhedron_3 class for (self-) intersections. The main difference are the numerous cases of incidences between triangles in the polyhedral surface that should not be reported as intersections, see the examples/Polyhedron/polyhedron_self_intersection.cpp example program in the CGAL distribution.
File Box_intersection_d/triangle_self_intersect.cpp
We modify the previous example, finding intersecting 3D triangles, and add an additional vector ptr that stores pointers to the bounding boxes, so that the intersection algorithm will work on a sequence of pointers and not on a sequence of boxes. The change just affects the preparation of the additional vector and the call of the box intersection function. The box intersection function (actually its default traits class) detects automatically that the value type of the iterators is a pointer type and not a class type.
In addition, the callback function report_inters() needs to be changed to work with pointers to boxes. The full example program looks as follows:
File Box_intersection_d/triangle_self_intersect_pointers.cpp
A note on performance: The algorithm sorts and partitions the input sequences. It is clearly costly to copy a large box compared to a simple pointer. However, the algorithm benefits from memory locality in the latter stages when it copies the boxes, while the pointers would refer to boxes that become wildly scattered in memory. These two effects, copying costs and memory locality, counteract each other. For small box sizes, i.e., small dimension, memory locality wins and one should work with boxes, while for larger box sizes one should work with pointers. The exact threshold depends on the memory hierarchy (caching) of the hardware platform and the size of the boxes, most notably the type used to represent the box coordinates. A concrete example; on a laptop with an Intel Mobile Pentium4 running at 1.80GHz with 512KB cache and 254MB main memory under Linux this version with pointers was 20% faster than the version above that copies the boxes for 10000 boxes, but the picture reversed for 100000 boxes, where the version above that copies the boxes becomes 300% faster.
Note that switching to the built-in type float is supported by the box intersection algorithm, but the interfacing with the CGAL bounding box Bbox_3 would not be that easy. In particular, just converting from the double to the float representation incurs rounding that needs to be controlled properly, otherwise the box might shrink and one might miss intersections.
Boxes can be interpreted by the box intersection algorithm as closed or as half-open boxes, see also Section Definition. Closed boxes support zero-width boxes and they can intersect at their boundaries, while half-open boxes always have a positive volume and they only intersect iff their interiors overlap. The choice between closed or half-open boxes is selected with the topology parameter and its two values:
The example program uses a two-dimensional box with int coordinates and id-numbers that are by default explicitly stored. We create the same boxes as in the minimal example in Section Minimal Example for Intersecting Boxes. We create a \( 3 \times 3\) grid of boxes, and two boxes for the query sequence, namely the box at the center and the box from the upper-right corner of the grid.
We write a more involved callback function object Report that stores an output iterator and writes the id-number of the box in the first argument to the output iterator. We also provide a small helper function report() that simplifies the use of the function object.
We call the box intersection algorithm twice; once for the default topology, which is the closed box topology, and once for the half-open box topology. We sort the resulting output for better readability and verify its correctness with the check1 and check2 data. For the closed box topology, the center box in query intersects all boxes, and the upper-right box in query intersects the four boxes of the upper-right quadrant in boxes. Almost all intersections are with the box boundaries, thus, for the half-open topology only one intersection remains per query box, namely its corresponding box in boxes. So, the output of the algorithm will be:
0 1 2 3 4 4 5 5 6 7 7 8 8 4 8
For the second box intersection function call we have to specify the cutoff parameter explicitly. See the Section Runtime Performance below for a detailed discussion.
File Box_intersection_d/box_grid.cpp
The implemented algorithm is described in [2] as version two. Its performance depends on a cutoff parameter. When the size of both iterator ranges drops below the cutoff parameter the function switches from the streamed segment-tree algorithm to the two-way-scan algorithm, see [2] for the details.
The streamed segment-tree algorithm needs \(O(n \log^d (n) + k)\) worst-case running time and \(O(n)\) space, where \( n\) is the number of boxes in both input sequences, \( d\) the (constant) dimension of the boxes, and \( k\) the output complexity, i.e., the number of pairwise intersections of the boxes. The two-way-scan algorithm needs \(O(n \log (n) + l)\) worst-case running time and \(O(n)\) space, where \( l\) is the number of pairwise overlapping intervals in one dimensions (the dimension where the algorithm is used instead of the segment tree). Note that \( l\) is not necessarily related to \( k\) and using the two-way-scan algorithm is a heuristic.
Unfortunately, we have no general method to automatically determine an optimal cutoff parameter, since it depends on the used hardware, the runtime ratio between callback runtime and segment-tree runtime, and of course the number of boxes to be checked and their distribution. In cases where the callback runtime is dominant, it may be best to make the threshold parameter small. Otherwise a cutoff \( =\sqrt{n}\) can lead to acceptable results. For well distributed boxes the original paper [2] gives optimal cutoffs in the thousands. Anyway, for optimal runtime some experiments to compare different cutoff parameters are recommended.
To demonstrate that box intersection can be done quite fast, different box sequences are intersected in the range between 4 and 800000 boxes total. We use three-dimensional default boxes of closed topology with float coordinates and without additional data fields. The algorithm works directly on the boxes, not on pointer to boxes. Each box intersection is reported to an empty dummy callback.
For each box set, a near-optimal cutoff parameter is determined using an adaptive approximation. The runtime required for streaming is compared against usual scanning. Results on a Xeon 2.4GHz with 4GB main memory can be seen in Figure 98.1. For a small number of boxes, pure scanning is still faster than streaming with optimal cutoff, which would just delegate the box sets to the scanning algorithm. As there are more and more boxes, the overhead becomes less important.
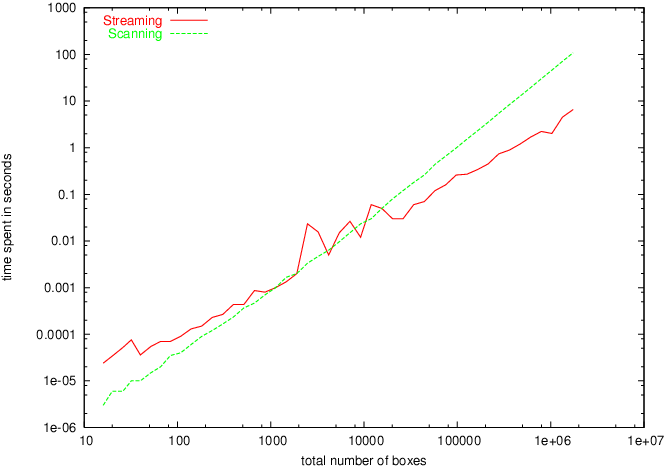
Figure 98.1 Runtime comparison between the scanning and the streaming algorithm.
The example in the previous Section Example Using the Topology and the Cutoff Parameters uses an array to provide the coordinates and then creates another array for the boxes. In the following example we write our own box class Box that we can initialize directly with the four coordinates and create the array of boxes directly. We also omit the explicitly stored id-number and use the address of the box itself as id-number. This works only if the boxes do not change their position, i.e., we work with pointers to the boxes in the intersection algorithm.
We follow with our own box class Box the BoxIntersectionBox_d concept, which allows us to reuse the default traits implementation, i.e., we can use the same default function call to compute all intersections. See the example in the next section for a self-written traits class. So, in principle, the remainder of the example stays the same and we omit the part from the previous example for brevity that illustrates the half-open box topology.
The requirements for the box implementation are best studied on the reference manual page of BoxIntersectionBox_d. In a nutshell, we have to define the type NT for the box coordinates and the type ID for the id-number. Member functions give access to the coordinates and the id-number. A static member function returns the dimension.
File Box_intersection_d/custom_box_grid.cpp
Given a set of 3D points, we want to find all pairs of points that are less than a certain distance apart. We use the box intersection algorithm to find good candidates, namely those that are less than this specified distance apart in the \( L_\infty\) norm, which is a good approximation of the Euclidean norm.
We use an unusual representation for the box, namely pointers to the 3D points themselves. We implement a special box traits class that interprets the point as a box of the dimensions \( [-\)eps \( ,+\)eps \( ]^3\) centered at this point. The value for eps is half the specified distance from above, i.e., points are reported if their distance is smaller than 2*eps.
The requirements for the box traits class are best studied on the reference manual page of BoxIntersectionTraits_d. In a nutshell, we have to define the type NT for the box coordinates, the type ID for the id-number, and the type Box_parameter similar to the box handle, here Point_3* since we work with the pointers. All member functions in the traits class are static. Two functions give access to the max and min coordinates that we compute from the point coordinates plus or minus the eps value, respectively. For the id-number function the address of the point itself is sufficient, since the points stay stable. Another function returns the dimension.
The report callback function computes than the Euclidean distance and prints a message for points that are close enough.
Note that we need to reserve sufficient space in the points vector to avoid reallocations while we create the points vector and the boxes vector in parallel, since otherwise the points vector might reallocate and invalidate all pointers stored in the boxes so far.
File Box_intersection_d/proximity_custom_box_traits.cpp
Given two polylines we want to know if they intersect. This implementation creates a box for each segment of the polyline and creates two sets of boxes. The callback throws an exception as soon as an intersection is detected.
File Box_intersection_d/box_d_do_intersect_polylines.cpp
Lutz Kettner and Andreas Meyer implemented the algorithms starting from the publication [2]. We had access to the original C implementation of Afra Zomorodian, which helped clarifying some questions, and we are grateful to the help of Afra Zomorodian in answering our questions during his visit. We thank Steve Robbins for an excellent review for this package. Steve Robbins provided an independent and earlier implementation of this algorithm, however, we learned too late about this implementation.