|
CGAL 6.1.1 - 2D Movable Separability of Sets
|
|
CGAL 6.1.1 - 2D Movable Separability of Sets
|
Movable Separability of Sets [2] is a class of problems that deal with moving sets of objects, such as polygons in the plane; the challenge is to avoid collisions between the objects while considering different kinds of motions and various definitions of separation. The Moving sofa problem or sofa problem is a classic member of this class. It is a two-dimensional idealization of real-life furniture-moving problems; it asks for the rigid two-dimensional shape of largest area \(A\) that can be maneuvered through an L-shaped planar region with legs of unit width [3]. The area \(A\) thus obtained is referred to as the sofa constant. The exact value of the sofa constant is an open problem; see Figure 26.1. These problems become progressively more challenging as the allowable set of separation motions becomes more complex (have more degrees of freedom), the number of objects involved grows, or the shape of the objects becomes more complicated.
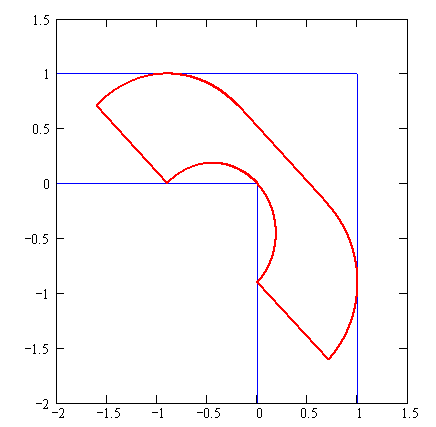
Figure 26.1 The Hammersley sofa has area 2.2074 but is not the largest solution.
At this point this package provides solutions to one subclass of problems related to 2D castings. In particular, each of these solutions handles a single moving polygon and a single stationary polygon, and considers a single translation of the moving polygon.
Casting is a manufacturing process where liquid material is poured into a cavity inside a mold, which has the shape of a desired product. (The mold can take any shape and form as long as it has a cavity of the desired shape.) After the material solidifies, the product is pulled out of the mold. Typically a mold is used to manufacture numerous copies of a product. The challenge is designing a proper mold, such that the solidified product can be separated from its mold without breaking it.
This package provides a function called CGAL::Set_movable_separability_2::Single_mold_translational_casting::top_edges() that, given a simple closed polygon \(P\), determines whether a cavity (of a mold in the plane) that has the shape of \(P\) can be used so that the polygon \(P\) could be pulled out of the mold without colliding into the mold (but possibly sliding along the mold boundary); see Figure 26.2 for an illustration. In reality, the mold of a castable polygon must be rotated before the polygon is casted, such that one edge becomes parallel to the \(x\)-axis and is located above all other edges; such an edge is referred to as a top edge. A polygon may have up to four edges that can serve as top edges. If the polygon is castable, the function computes the set of top edges of such cavities and the corresponding closed ranges of pullout directions in the plane.

Figure 26.2 Two castable polygons (light grey) in their molds (darker grey) and valid pullout directions on the left. Two non-castable polygons on the right.
The input polygon must satisfy two conditions as follows. First, it has to be simple. Essentially, a simple polygon is topologically equivalent to a disk; see Chapter 2D Regularized Boolean Set-Operations for the precise definition of simple polygons. Secondly, any consecutive three vertices cannot be collinear. If you suspect that the input polygon may not satisfy the latter condition, preprocess the polygon to eliminate this ill-condition.
The implementation is based on an algorithm developed by Shamai and Halperin; see [1] for the generalization of the algorithm to 3D. The time and space complexities are in \(O(n)\) and \(O(1)\), respectively. In order to ensure robustness and correctness you must use a kernel that guarantees exact constructions as well as exact predicates, e,g,. Exact_predicates_exact_constructions_kernel.
The following example computes the top edges and their pullout directions of an input polygon read from a file and reports the results.
File Set_movable_separability_2/top_edges_single_mold_trans_cast.cpp
This package provides two additional functions, namely, CGAL::Set_movable_separability_2::Single_mold_translational_casting::pullout_directions() and CGAL::Set_movable_separability_2::Single_mold_translational_casting::is_pullout_direction(). The former accepts a simple closed polygon \(P\) and an edge \(e\) of the polygon \(P\); it determines whether \(e\) is a top edge of \(P\), and if so, it computes the range of pullout directions of \(e\). The latter is overloaded with two versions: The first version accepts a simple closed polygon \(P\) and a direction \(d\); it determines whether \(d\) is a pullout direction of some top edge of \(P\). The other version accepts, in addition, an edge \(e\) of the polygon \(P\); it determines whether \(d\) is a pullout direction of \(e\).
Overloads of each of the functions above that accept (i) an additional argument that indicates the orientation of the input polygon or (ii) an additional traits argument, or (iii) both, are also provided by the package.