|
CGAL 6.1 - 2D Regularized Boolean Set-Operations
|
|
CGAL 6.1 - 2D Regularized Boolean Set-Operations
|

Figure 17.1 Examples of Boolean set-operations on general polygons.
This package consists of the implementation of Boolean set-operations on point sets bounded by weakly \( x\)-monotone curvesA continuous planar curve \( C\) is weakly \( x\)-monotone if every vertical line intersects it at most once, or if it is vertical. Hereafter we refer to weakly \( x\)-monotone curves as \( x\)-monotone curves. in 2-dimensional Euclidean space. In particular, it contains the implementation of regularized Boolean set-operations, intersection predicates, and point containment predicates. Figure 17.1 shows simple examples of such operations.
Ordinary Boolean set-operations, which distinguish between the interior and the boundary of a polygon, are not implemented within this package. The Chapter 2D Boolean Operations on Nef Polygons supports these operations for (linear) polygons.
In the rest of this chapter we use, unless otherwise stated, the traditional notation to denote regularized operations; e.g., \( P \cap Q\) means the regularized intersection of \( P\) and \( Q\).
Our package supports the following Boolean set-operations on two point sets \( P\) and \( Q\) that each is the union of one or more general polygons:
In general, the set \( R\), resulting from a regularized Boolean set-operation, is considered as being a closed point-set; see definition of regularized boolean set operations below.
In the rest of this chapter we review the Boolean set-operations package in more depth. In Section Boolean Set-Operations on Linear Polygons we focus on Boolean set-operations on linear polygons, introducing the notion of polygons with holes and of a general polygon set. Section Boolean Set-Operations on General Polygons introduces general polygons. We first discuss polygons whose edges are either line segments or circular arcs and then explain how to construct and use general polygons whose edges can be arbitrary weakly \( x\)-monotone curves.
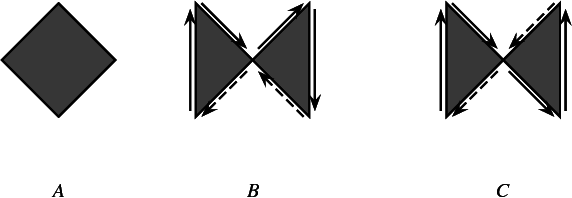
Figure 17.2 Examples of polygons. (a) A simple polygon. (b) A relatively simple polygon (c) A polygon that is neither simple nor relatively simple.
The counterclockwise cyclic sequence of alternating polygon edges and polygon vertices is referred to as the polygon (outer) boundary.
A polygon whose curves are pairwise disjoint in their interior, and whose vertices' degree equals two is defined as a Simple polygon. Such a polygon has a well-defined interior and exterior and is topologically equivalent to a disk. Note that while traversing the edges of the relatively simple polygon illustrated above (B), no curve is crossed over.
A Relatively simple polygon allows vertices with a degree \(> 2\), but all of its edges are disjoint in their interior. Furthermore, it must be an orientable polygon. Namely when it is inserted into an arrangement and its outer boundary is traversed, the same face is adjacent to all of the halfedges (no crossing over any curve during the traversal). Note that while polygon C has the same curves as polygon B, traversal of the curves leads to crossing over a previously traversed curve, and is therefore neither simple nor relatively simple.
A polygon in our context must be relatively simple and its outer boundary vertices must be ordered in a counterclockwise direction around the interior of the polygon. We extend the notion of a polygon to a point set in \( \mathbb{R}^2\) that has a topology of a polygon and its boundary edges must map to \( x\)-monotone curves, and refer to it as a general polygon. We sometimes use the term polygon instead of general polygon for simplicity hereafter.
A polygon with holes represents a point set that may be bounded or unbounded. In case of a bounded set, its outer boundary is represented as a relatively simple (but not necessarily simple) polygon, whose vertices are oriented in a counterclockwise order around the interior of the set. In addition, the set may contain holes, where each hole is represented as a simple polygon, whose vertices are oriented in a clockwise order around the interior of the hole. Note that an unbounded polygon without holes spans the entire plane. Vertices of holes may coincide with vertices of the boundary.
In our context, a polygon must uphold the following conditions:
In our context, a polygon with holes must uphold the following conditions:
Pairwise disjoint holes (on interior) - the polygon's holes must be pairwise disjoint, except for intersection on a joint vertex/vertices.
The basic library of CGAL includes the Polygon_2<Kernel,Container> class-template that represents a linear polygon in the plane. The polygon is represented by its vertices stored in a container of objects of type Kernel::Point_2. The polygon edges are line segments (Kernel::Segment_2 objects) between adjacent points in the container. By default, the Container is a vector of Kernel::Point_2 objects.
The following function demonstrates how to use the basic access functions of the Polygon_2 class. It accepts a polygon \( P\) and prints it in a readable format:
In this section we use the term polygon to indicate a Polygon_2 instance, namely, a polygon having linear edges. General polygons are only discussed in Section Boolean Set-Operations on General Polygons.
The basic components of our package are the free (global) functions complement() that accepts a single Polygon_2 object, and intersection(), join(),The function that computes the union of two polygons is called join(), since the word union is reserved in C++. difference(), symmetric_difference() and the predicate do_intersect() that accept two Polygon_2 objects as their input. We explain how these functions should be used through several examples in the following sections.

Testing whether two polygons intersect results with a Boolean value, and does not require any additional data beyond the provision of the two input polygons. The example listed below tests whether the two triangles depicted on the right intersect. It uses, as do the other example programs in this chapter, the auxiliary header file bso_rational_nt.h, which defines the type Number_type as GMP's rational number-type (Gmpq), or as the number type Quotient<MP_Float> that is included in the support library of CGAL, based on whether the GMP library is installed or not. It also uses the function print_polygon.h listed above, which is located in the header file print_utils.h.
File Boolean_set_operations_2/do_intersect.cpp
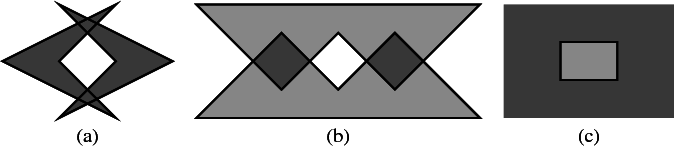
Figure 17.3 Operations on simple polygons. (a) The union of two polygons, resulting in a point set whose outer boundary is defined by a simple polygon and contains a polygonal hole in its interior. (b) The intersection (darkly shaded) of two polygons (lightly shaded), resulting in two disjoint polygons. (c) The complement (darkly shaded) of a simple polygon (lightly shaded).
In many cases a binary operation that operates on two simple polygons that have no holes may result in a set of polygons that contain holes in their interior (see Figure 17.3 (a)), or a set of disjoint polygons (see Figure 17.3 (b); a similar set may result from the union, or the symmetric difference, of two disjoint polygons). Moreover, the complement of a simple polygon is an unbounded set that contains a hole; see Figure 17.3 (c).
Regular sets are closed under regularized Boolean set-operations. These operations accept as input, and may result as output, polygons with holes. A polygon with holes represents a point set that may be bounded or unbounded. In case of a bounded set, its outer boundary is represented as a relatively simple (but not necessarily simple) polygon, whose vertices are oriented in a counterclockwise order around the interior of the set. In addition, the set may contain holes, where each hole is represented as a simple polygon, whose vertices are oriented in a clockwise order around the interior of the hole. Note that an unbounded polygon without holes spans the entire plane. Vertices of holes may coincide with vertices of the boundary; see below for an example.
A point set represented by a polygon with holes is considered to be closed. Therefore, the boundaries of the holes are parts of the set (and not part of the holes). The exact definition of the obtained polygon with holes as a result of a Boolean set-operation or a sequence of such operations is closely related to the definition of regularized Boolean set-operations, being the closure of the interior of the corresponding ordinary operation as explained next.

Consider, for example, the regular set depicted on the right, which is the result of the union of three small triangles translated appropriately. Alternatively, the same set can be reached by taking the difference between a large triangle and a small upside-down triangle. In general, there are many ways to arrive at a particular point set. However, the set of polygons with holes obtained through the application of any sequence of operations is unique. The set depicted on the right is represented as a single polygon having a triangular outer boundary with a single triangular hole in its interior - and not as three triangles that have no holes at all. As a general rule, if two point sets are connected, then they belong to the same polygon with holes.
The class template Polygon_with_holes_2<Kernel,Container> represents polygons with holes as described above, where the outer boundary and the hole boundaries are realized as Polygon_2<Kernel,Container> objects. Given an instance \( P\) of the Polygon_with_holes_2 class, you can use the predicate is_unbounded() to check whether \( P\) is a unbounded set. If it is bounded, you can obtain the counterclockwise-oriented polygon that represents its outer boundary through the member function outer_boundary(). You can also traverse the holes of \( P\) through holes_begin() and holes_end(). The two functions return iterators of the nested type Polygon_with_holes_2::Hole_const_iterator that defines the valid range of \( P\)'s holes. The value type of this iterator is Polygon_2.
The following function demonstrates how to traverse a polygon with holes. It accepts a Polygon_with_holes_2 object and uses the auxiliary function print_polygon() to prints all its components in a readable format:
The simple versions of the free functions mentioned therefore accept two Polygon_2 object \( P\) and \( Q\) as their input, while their output is given using polygon with holes instances:
complement(P) therefore returns a polygon-with-holes object that represents the complement of \( P\). join(P, Q, R) therefore returns a Boolean value indicating whether \( P \cap Q \neq \emptyset\). If the two polygons are not disjoint, it assigns the polygon with holes object \( R\) (which it accepts by reference) with the union of the regularized union operation \( P \cup Q\). intersection(P, Q, oi), difference(P, Q, oi) and symmetric_difference(P, Q, oi), all have a similar interface. As the result of these operation may consist of several disconnected components, they all accept an output iterator oi, whose value type is Polygon_with_holes_2, and adds the output polygons to its associated container. The following example demonstrates the usage of the free functions join() and intersection() for computing the union and the intersection of the two simple polygons depicted in Figure 17.3 (b). The example uses the auxiliary function print_polygon_with_holes() listed above, which is located in the header file print_utils.h under the examples folder.
File Boolean_set_operations_2/simple_join_intersect.cpp
We have demonstrated that free functions that perform Boolean set operations on simple polygons may output polygons with holes. In addition to these functions, the Boolean set-operations package provides the following overridden free functions that accept General_polygon_with_holes_2 objects as their input: complement(), intersection(), join(), difference(), symmetric_difference(), and do_intersect() The prototypes of most functions are the same as of their simpler counterparts that operate on simple polygons. The only exception is complement(P, oi), which outputs a range of polygons with holes that represents the complement of the polygon with holes \( P\).

The following example demonstrates how to compute the symmetric difference between two sets that contain holes. Each set is a rectangle that contains a rectangular hole in its interior, such that the symmetric difference between the two sets is a single polygon that contains of five holes:
File Boolean_set_operations_2/symmetric_difference.cpp
In some cases it is convenient to connect the outer boundary of a polygon with holes with the holes inside it. The function connect_holes() accepts a polygon with holes, and connects the topmost vertex in each hole with the polygon feature located directly above it (a vertex or an edge of the outer boundary, or of another hole). It produces an output sequence of points that match the traversal of all vertices in the connected polygon (note that there are additional vertices, induced by the vertical walls).
File Boolean_set_operations_2/connect_polygon.cpp
The result of a regularized operation on two polygons (or polygons with holes) \( P\) and \( Q\) is typically a collection of several disconnected polygons with holes. It is only natural to represent such a collection in terms of a class, making it possible to operate on the set resulting from computing, for example, \( P \setminus Q\).
A central component in the Boolean set-operations package is the Polygon_set_2<Kernel, Container, Dcel> class-template. An instance of this class represents a point set formed by the collection of several disconnected polygons with holes. It employs the Arrangement_2 class to represent this point set in the plane as a planar arrangement; see Chapter 2D Arrangements. The instantiated Dcel type is used to represent the underlying internal arrangement. It must model the concept GeneralPolygonSetDcel, and defaults to Gps_default_dcel. You can override this default, with a different DCEL class, typically an extension of the default. Overriding the default is necessary only if you intend to obtain the underlying internal arrangement and process it further.
An instance \( S\) of a Polygon_set_2 class usually represents the result of a sequence of operations that were applied on some input polygons. The representation of \( S\) is unique, regardless of the particular sequence of operations that were applied in order to arrive at it.
In addition, a polygon-set object can be constructed from a single polygon object or from a polygon-with-holes object. Once constructed, it is possible to insert new polygons (or polygons with holes) into the set using the insert() method, as long as the inserted polygons and the existing polygons in the set are disjoint. The Polygon_set_2 class also provides access functions for obtaining the polygons with holes it contains, and a few queries. An important query is S.oriented_side(q), which determined whether the query point \(
q\) is contained in the interior of the set \( S\), lies on the boundary of the set, or neither.
Similar to the Polygon_set_2 class template, which applies to linear polygons (or polygons with holes), the General_polygon_set_2 class applies to general polygons (or general polygons with holes). Each of these class templates defines the predicate do_intersect() and the methods complement(), intersection(), join(), difference() and symmetric_difference() as member functions. The operands to these functions may be simple polygons (Polygon_2 or General_polygon_2 objects), polygons with holes (Polygon_with_holes_2 or General_polygon_with_holes_2 objects), or polygon sets (cpolygon_set_2 or General_polygon_set_2 objects). Each of the aforementioned free functions is actually realized by a set overriding member function.
member functions of the Polygon_set_2 (respectively General_polygon_set_2) that perform Boolean set-operations come in two flavors: for example, S.join(P, Q) computes the union of \( P\) and \( Q\) and assigned the result to \( S\), while S.join(P) performs the operation \( S \longleftarrow S \cup P\). Similarly, S.complement(P) sets \( S\) to be the complement of \(
P\), while S.complement() assigns \( S\) with its complement.
The free functions reviewed in Section Polygons with Holes serve as a wrapper for the polygon-set class, and are only provided for convenience. A typical such function constructs a pair of General_polygon_set_2 objects, invokes the appropriate method to apply the desired Boolean operation, and transforms the resulting polygon set to the required output format. Thus, when several operations are performed in a sequence, it is much more efficient to use the member functions of the General_polygon_set_2 type directly, as the extraction of the polygons from the internal representation for some operation, and the reconstruction of the internal representation for the succeeding operation could be time consuming.

The next example performs a sequence of three Boolean set-operations. First, it computes the union of two simple polygons depicted in Figure 17.3 (a). It then computes the complement of the result of the union operation. Finally, it computes the intersection of the result of the complement operation with a rectangle, confining the final result to the area of the rectangle. The resulting set \( S\) is comprised of two components: a polygon with a hole, and a simple polygon contained in the interior of this hole.
File Boolean_set_operations_2/sequence.cpp
If you want to compute the union of a polygon \( P\) ( \( P\) may be a simple polygon or a polygon-with-holes object) with a general-polygon set \( R\), and store the result in \( R\), you can construct a polygon set \( S(P)\), and apply the union operation as follows:
As a matter of fact, you can apply the union operation directly:
However, if you know that the polygon does not intersect any one of the polygons represented by \( R\), you can use the more efficient method insert():
As insert() assumes that \( P \cap R = \emptyset\), it does not try to compute intersections between the boundaries of \( P\) and of \( R\). This fact significantly speeds up the insertion process in comparison with the insertion of a non-disjoint polygon that intersects \( R\).
The insert() function is also overloaded, so it can also accept a range of polygons. When a range of polygons are inserted into a polygon set \( S\), all the polygons in the range and the polygons represented by \( S\) must be pairwise disjoint in their interiors.
There are a few options to compute the union of a set of polygons \( P_1, \ldots P_m\). You can do it incrementally as follows. At each step compute the union of \( S_{k-1} = \bigcup_{i=1}^{k-1}{P_i}\) with \( P_{k}\) and obtain \( S_k\). Namely, if the polygon set is given as a pair of iterator [begin, end), the following loop computes their union in \( S\).
A second option is to use a divide-and-conquer approach. You bisect the set of polygons into two sets. Compute the union of each set recursively and obtain the partial results in \( S_1\) and \( S_2\), and finally, you compute the union \( S_1 \cup S_2\). However, the union operation can be done more efficiently for sparse polygons, having a relatively small number of intersections, using a third option that simultaneously computes the union of all polygons. This is done by constructing a planar arrangement of all input polygons, utilizing the sweep-line algorithm, then extracting the result from the arrangement. Similarly, it is also possible to aggregately compute the intersection \( \bigcap_{i=1}^{m}{P_i}\) of a set of input polygons.
Our package provides the free overloaded functions join() and intersection() that aggregately compute the union and the intersection of a range of input polygons. There is no restriction on the polygons in the range; naturally, they may intersect each other. The package provides the overloaded free function do_intersect(begin, end) that determines whether the polygons in the range defined by the two input iterators [begin, end) intersect.
The class General_polygon_set_2 also provides equivalent member functions that aggregately operate on a range of input polygons or polygons with holes. When such a member function is called, the general polygons represented by the current object are considered operands as well. Thus, you can easily compute the union of our polygon range as follows:
All the free function-templates that apply Boolean set operations accept an optional traits argument; see next Section for more information. If a traits class is not provided, a default one that can handle the type of the curves that comprise the boundaries of the input polygons is selected. You somehow can influence this selection using a template parameter as described below.
The set of free function-templates that handle (linear) polygons include overloaded versions that are parameterized by the template parameter UsePolylines. For each such function template the UsePolylines template parameter determmines whether to treat the boundary of each input (linear) polygon as a cyclic sequence of single ( \(x\)-monotone) segments or as a cyclic sequence of ( \(x\)-monotone) polylines. By default, UsePolylines is set to CGAL::Tag_true, which implies that the boundary of the each input (linear) polygon is treated as a cyclic sequence of ( \(x\)-monotone) polylines. In most cases this behavior is superior (that is, less time-consuming) because the number of events handled as part of the execution of the plane-sweep algorithm is reduced. In cases where the boundaries of the input polygons frequently intersect, treating them as polylines may become less efficient. In these cases substitute the UsePolylines template parameter with CGAL::Tag_false to restore the original behavior (where the boundary of each input linear polygon is treated as a cyclic sequence of single \(x\)-monotone segments).
A Boolean set operation can be apppplied on general polygons (or general polygons with holes) directly using an instance of the class template General_polygon_set_2 or by using a free function, which internally uses an instance of the class template General_polygon_set_2. Similarly, a Boolean set operation can be apppplied on linear polygons (or linear polygons with holes) directly using an instance of the class template Polygon_set_2 or by using a free function, which internally uses an instance of the class template Polygon_set_2 by default. An instance of the Polygon_set_2 class template treats every edge of the polygon as a single ( \(x\)-monotone) segment, as it utilizes, in turn, the Arr_segment_traits_2 class template; see Section Traits Classes for Line Segments and Linear Objects in the 2D Arrangements package.
If the UsePolylines template parameter is substitited with CGAL::Tag_true the following occurs:
Instead of using an instance of the Polygon_set_2 class template, as described above, an instance of the General_polygon_set_2 class template is used, which utilizes the Arr_polyline_traits_2 class template; see Section The Polyline and Polycurve Traits Classes in the 2D Arrangements package.
Each input linear polygon (respectively linear polygon with holes) is converted into a general polygon (respectively general polygon with holes) bounded by \(x\)-monotone polylines. Then, the resulting general polygons, which are also bounded by \(x\)-monotone polylines, are converted back to standard polygons.

In previous sections only ordinary (linear) polygons were dealt with. Namely, closed point sets bounded by piecewise linear curves. The Boolean set-operations package allows a more general geometric mapping of the polygon edges. The operations provided by the package operate on point sets bounded by \( x\)-monotone segments of general curves (e.g., conic arcs and segments of polynomial functions). For example, the point set depicted on the right is a general polygon bounded by two \( x\)-monotone circular arcs that correspond to the lower half and the upper half of a circle, respectively.
Using the topological terminology, a general polygon can represent any simply-connected point set whose boundary is a strictly simple curve. Such a polygon is a model of the GeneralPolygon_2 concept. A model of this concept must fulfill the following requirements:

The concept GeneralPolygonWithHoles_2 is defined in an analogous way to the definition of linear polygons with holes. A model of this concept represent a bounded or an unbounded set that may not be simply connected, and must provide the following operations:
In Section Boolean Set-Operations on Linear Polygons we introduce the classes Polygon_2 and Polygon_with_holes_2 that model the concepts GeneralPolygon_2 and GeneralPolygonWithHoles_2 respectively. In this section we introduce other models of these two concepts.
The central class-template General_polygon_set_2<Traits,Dcel> is used to represent point sets that are comprised of a finite number of pairwise disjoint general polygons with holes, and provides various Boolean set-operations on such sets. It is parameterized by a traits class and a DCEL class. The former defines the type of points used to represent polygon vertices and the type of \( x\)-monotone curves that represent the polygon edges. The traits class also provides primitive geometric operations that operate on objects of these types. The DCEL class is used to represent the underlying internal Arrangement_2 data structure. The instantiated Dcel type is used to represent the underlying internal arrangement. It must model the concept GeneralPolygonSetDcel, and defaults to Gps_default_dcel. You can override this default, with a different DCEL class, typically an extension of the default. Overriding the default is necessary only if you intend to obtain the underlying internal arrangement and process it further.
An instantiated General_polygon_set_2 class defines the nested types General_polygon_set_2<Traits,Dcel>::Polygon_2 and General_polygon_set_2<Traits,Dcel>::Polygon_with_holes_2, which model the concepts GeneralPolygon_2 and GeneralPolygonWithHoles_2 respectively.
The traits class used to instantiate the General_polygon_set_2 class template must model the concept GeneralPolygonSetTraits_2, and is tailored to handle a specific family of curves. The concept GeneralPolygonSetTraits_2 refines the concept AosDirectionalXMonotoneTraits_2 specified next.
The concept AosDirectionalXMonotoneTraits_2 refines the concept AosXMonotoneTraits_2 (see Section Inserting X-monotone Curves in the 2D Arrangements package). Thus, a model of this concept must define the type X_monotone_curve_2, which represents an \( x\)-monotone curve, and the type Point_2, with represents a planar point. Such a point may be an endpoint of an \( x\)-monotone curve or an intersection point between two curves. It must also provide various geometric predicates and operations on these types listed by the base concept, such as determining whether a point lies above or below an \( x\)-monotone curve, computing the intersections between two curves, etc. Note that the base concept does not assume that \( x\)-monotone curves are directed: an \( x\)-monotone curve is not required to have a designated source and target, it is only required to determine the left (lexicographically smaller) and the right (lexicographically larger) endpoints of a given curve.
The AosDirectionalXMonotoneTraits_2 concept treats its \( x\)-monotone curves as directed objects. It thus requires two additional operations on \( x\)-monotone curves:
The traits classes Arr_segment_traits_2, Arr_non_caching_segment_traits_2, Arr_circle_segment_traits_2, Arr_conic_traits_2 and Arr_rational_function_traits_2, which are bundled in the Arrangement_2 package and distributed with CGAL, are all models of the refined concept AosDirectionalXMonotoneTraits_2.The Arr_polyline_traits_2 class is not a model of the, AosDirectionalXMonotoneTraits_2 concept, as the \( x\)-monotone curve it defines is always directed from left to right. Thus, an opposite curve cannot be constructed. However, it is not very useful to construct a polygon whose edges are polylines, as an ordinary polygon with linear edges can represent the same entity.
Just as with the case of computations using models of the AosXMonotoneTraits_2 concept, operations are robust only when exact arithmetic is used. When inexact arithmetic is used, (nearly) degenerate configurations may result in abnormal termination of the program or even incorrect results.
Two traits classes are distributed with CGAL. The first one is named Gps_segment_traits_2, and it is used to perform Boolean set-operations on ordinary polygons and polygons with holes. In fact, the class Polygon_set_2 introduced in Section Operating on Polygon Sets is a specialization of General_polygon_set_2<Gps_segment_traits_2>. This class defined its polygon and polygon with holes types, such that the usage of this traits class is encapsulated in the polygon-set class.
The other predefined traits class is named Gps_circle_segment_traits_2<Kernel> and is parameterized by a geometric CGAL kernel. By instantiating the General_polygon_set_2 with this traits class, we obtain the representation of a polygon whose boundary may be comprised of line segments and circular arcs. The circle-segment traits class provides predicates and constructions on non-linear objects; yet, it uses only rational arithmetic and is very efficient as a consequence.
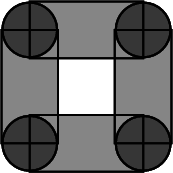
The following example uses the Gps_circle_segment_traits_2 class to compute the union of four rectangles and four circles. Each circle is represented as a general polygon having two \( x\)-monotone circular arcs. The union is computed incrementally, resulting with a single polygon with a single hole, as depicted on the right. Note that as the four circles are disjoint, their union is computed with the insert method, while the union with the rectangles is computed with the join operator.
File Boolean_set_operations_2/circle_segment.cpp
The concept GeneralPolygon_2 and its generic model General_polygon_2<ArrDirectionalXMonotoneTraits> facilitate the production of general-polygon set traits classes. A model of the concept GeneralPolygon_2 represents a simple point-set in the plane bounded by \( x\)-monotone curves. As opposed to the plain Traits::Polygon_2 type defined by any traits class, it must define the type X_monotone_curve_2, which represents an \( x\)-monotone curve of the point-set boundary. It must provide a constructor from a range of such curves, and a pair of methods, namely curves_begin() and curves_end(), that can be used to iterate over the point-set boundary curves.
The class-template General_polygon_2<ArrDirectionalXMonotoneTraits> models the concept GeneralPolygon_2. Its sole template parameter must be instantiated with a model of the concept AosDirectionalXMonotoneTraits_2 from which it obtains the X_monotone_curve_2 type. It uses the geometric operations on this type provided by such a model to maintain a container of directed curves of type X_monotone_curve_2, which represents a boundary of the general polygon.
The class-template Gps_traits_2<ArrDirectionalXMonotoneTraits,GeneralPolygon> models the concept GeneralPolygonSetTraits_2, and can be used to instantiate the class template General_polygon_set_2. It serves as an adapter for a geometric traits class, which models the concept AosDirectionalXMonotoneTraits_2. It can be used for performing set-operations on general polygons. The implementation of the adapter is rather simple, as it is derived from the instantiated template-parameter ArrXMonotoneTraits_2 inheriting its necessary types and methods. It further exploits the methods provided by the instantiated parameter GeneralPolygon, which is a model of the concept GeneralPolygon_2. By default, the GeneralPolygon parameter is defined as General_polygon_2<AosDirectionalXMonotoneTraits_2>.
The code excerpt listed below defines a general-polygon set type that can be used to perform Boolean set-operations on point sets bounded by the \( x\)-monotone curve type defined by the arrangement-traits class Arr_traits_2, which is some representative model of the concept AosDirectionalXMonotoneTraits_2.

Instantiating the arrangement-traits Arr_traits_2 above with the traits class that handle Bézier curves Arr_Bezier_curve_traits_2, results with the definition of a general-polygon set type that can be used to perform Boolean set-operations on point sets bounded by Bézier curves.
The next example computes the intersection of two general polygons bounded by Bézier curves read from two input files respectively. The default input files our example uses (char_g.dat and char_m.dat) define two general polygons shaped in the form of the characters g and m in the Times New Roman font respectively. Their intersection comprises nine simple polygons, as depicted to the right.
Recall that every Bézier curve is defined by a sequence of control points that form chains (see Section A Traits Class for Planar Bézier Curves. The last control point of every curve must be identical to the first control point of its successor. The function read_Bezier_polygon() included in the example reads the curves from an input file until they form a closed chain, which is assumed to be the outer boundary of the polygon. If more curves are available, its starts constructing polygons that correspond to holes in the area bounded by the outer boundary. Note that this function is also responsible for subdividing the input Bézier curves into \( x\)-monotone subcurves, as required by the Gps_traits_2 adapter.
File Boolean_set_operations_2/bezier_traits_adapter.cpp
In Section Performing Aggregated Operations we describe how aggregated union and intersection operations can be applied to a collection of ordinary polygons or polygons with holes. Naturally, the aggregated operations can be applied also to collections of general polygons. As was the case with ordinary polygons, using aggregated operations is recommended when the number of intersections of the input polygons is of the same order of magnitude as the complexity of the result. If this is not the case, computing the result incrementally may prove faster.

The next example computes the union of eight unit discs whose centers are placed a unit distance from the origin, as depicted to the right. The example also allows users to provide a different number of discs through the command line.
File Boolean_set_operations_2/set_union.cpp