|
CGAL 6.1.1 - 3D Triangulation Data Structure
|
|
CGAL 6.1.1 - 3D Triangulation Data Structure
|
3D-triangulation data structures are meant to maintain the combinatorial information for 3D-geometric triangulations.
In CGAL, a triangulation data structure is a container of cells ( \( 3\)-faces) and vertices ( \( 0\)-faces). Following the standard vocabulary of simplicial complexes, an \( i\)-face \( f_i\) and a \( j\)-face \( f_j\) \( (0 \leq j < i \leq 3)\) are said to be incident in the triangulation if \( f_j\) is a (sub)face of \( f_i\), and two \( i\)-faces \( (0 \leq i \leq 3)\) are said to be adjacent if they share a common incident (sub)face.
Each cell gives access to its four incident vertices and to its four adjacent cells. Each vertex gives direct access to one of its incident cells, which is sufficient to retrieve all the incident cells when needed.
The four vertices of a cell are indexed with 0, 1, 2 and 3. The neighbors of a cell are also indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by \( i\) is opposite to the vertex with the same index (see Figure 49.1).
Edges ( \( 1\)-faces) and facets ( \( 2\)-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex of index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of indices i and j of c).
As CGAL explicitly deals with all degenerate cases, a 3D-triangulation data structure in CGAL can handle the cases when the dimension of the triangulation is lower than 3 (see Section Representation).
Thus, a 3D-triangulation data structure can store a triangulation of a topological sphere \( S^d\) of \( \mathbb{R}^{d+1}\), for any \( d \in \{-1,0,1,2,3\}\).
The second template parameter of the basic triangulation class (see Chapter 3D Triangulations) CGAL::Triangulation_3 is a triangulation data structure class. (See Chapter chapterTDS3.)
To ensure all the flexibility of the class CGAL::Triangulation_3, a model of a triangulation data structure must be templated by the base vertex and the base cell classes (see Representation): TriangulationDataStructure_3<TriangulationVertexBase_3,TriangulationCellBase_3>. The optional functionalities related to geometry are compulsory for this use as a template parameter of CGAL::Triangulation_3.
A class that satisfies the requirements for a triangulation data structure class must provide the following types and operations.
I/O
The information stored in the iostream is: the dimension, the number of vertices, the number of cells, the indices of the vertices of each cell, then the indices of the neighbors of each cell, where the index corresponds to the preceding list of cells. When dimension < 3, the same information is stored for faces of maximal dimension instead of cells.
CGAL::Triangulation_data_structure_3<Vb, Cb> Concepts | |
| concept | Cell |
The concept TriangulationDataStructure_3::Cell stores four Vertex_handles to its four vertices and four Cell_handles to its four neighbors. The vertices are indexed 0, 1, 2, and 3 in consistent order. The neighbor indexed \( i\) lies opposite to vertex i. More... | |
| concept | Cell_data |
| Various algorithms using a triangulation data structure, such as Delaunay triangulations or Alpha Shapes, must be able to associate a state to a cell elemental. For efficiency, this information must be stored directly within the cell. More... | |
| concept | Vertex |
The concept TriangulationDataStructure_3::Vertex represents the vertex class of a 3D-triangulation data structure. It must define the types and operations listed in this section. Some of these requirements are of geometric nature, they are optional when using the triangulation data structure class alone. They become compulsory when the triangulation data structure is used as a layer for the geometric triangulation class. (See Section Software Design.) More... | |
Types | |
| typedef unspecified_type | Vertex |
Vertex type, requirements are described in TriangulationDataStructure_3::Vertex. | |
| typedef unspecified_type | Cell |
Cell type, requirements are described in TriangulationDataStructure_3::Cell. | |
| typedef unspecified_type | Cell_data |
Cell data type, requirements are described in TriangulationDataStructure_3::Cell_data. | |
| typedef unspecified_type | size_type |
| Size type (unsigned integral type) | |
| typedef unspecified_type | difference_type |
| Difference type (signed integral type) | |
| typedef unspecified_type | Vertex_handle |
| typedef unspecified_type | Cell_handle |
| typedef unspecified_type | Concurrency_tag |
Can be CGAL::Sequential_tag, CGAL::Parallel_tag, or Parallel_if_available_tag. | |
| template<typename Vb2 > | |
| using | Rebind_vertex = unspecified_type |
| This is an advanced type. | |
| template<typename Cb2 > | |
| using | Rebind_cell = unspecified_type |
| This is an advanced type. | |
| typedef Triple< Cell_handle, int, int > | Edge |
(c,i,j) is the edge of cell c whose vertices indices are i and j. | |
| typedef std::pair< Cell_handle, int > | Facet |
(c,i) is the facet of c opposite to the vertex of index i. | |
Iterators | |
The following iterators allow one to visit all the vertices, edges, facets and cells of the triangulation data structure. They are all bidirectional, non-mutable iterators. Iterators are convertible to the corresponding handles, thus the user can pass them directly as arguments to the functions. | |
| typedef unspecified_type | Cell_iterator |
| typedef unspecified_type | Facet_iterator |
| typedef unspecified_type | Edge_iterator |
| typedef unspecified_type | Vertex_iterator |
Circulators | |
The following circulators allow us to visit all the cells and facets incident to a given edge. They are bidirectional and non-mutable.Circulators are convertible to the corresponding handles, thus the user can pass them directly as arguments to the functions. | |
| typedef unspecified_type | Facet_circulator |
| typedef unspecified_type | Cell_circulator |
Creation | |
| TriangulationDataStructure_3 () | |
| Default constructor. | |
| TriangulationDataStructure_3 (const TriangulationDataStructure_3 &tds1) | |
| Copy constructor. | |
| TriangulationDataStructure_3 & | operator= (const TriangulationDataStructure_3 &tds1) |
| Assignment operator. | |
| Vertex_handle | copy_tds (const TriangulationDataStructure_3 &tds1, Vertex_handle v=Vertex_handle()) |
tds1 is copied into tds. | |
| template<class TDS_src , class ConvertVertex , class ConvertCell > | |
| Vertex_handle tds | copy_tds (const TDS_src &tds_src, typename TDS_src::Vertex_handle v, const ConvertVertex &convert_vertex, const ConvertCell &convert_cell) |
tds_src is copied into this. | |
| void | swap (TriangulationDataStructure_3 &tds1) |
Swaps tds and tds1. | |
| void | clear () |
| Deletes all cells and vertices. | |
Access Functions | |
| int | dimension () const |
| The dimension of the triangulated topological sphere. | |
| size_type | number_of_vertices () const |
| The number of vertices. | |
| size_type | number_of_cells () const |
| The number of cells. | |
Non constant-time access functions | |
| size_type | number_of_facets () const |
| The number of facets. | |
| size_type | number_of_edges () const |
| The number of edges. | |
Setting | |
| void | set_dimension (int n) |
| This is an advanced function. | |
Queries | |
| bool | is_vertex (Vertex_handle v) const |
Tests whether v is a vertex of tds. | |
| bool | is_edge (Cell_handle c, int i, int j) const |
Tests whether (c,i,j) is an edge of tds. | |
| bool | is_edge (Vertex_handle u, Vertex_handle v, Cell_handle &c, int &i, int &j) const |
Tests whether (u,v) is an edge of tds. | |
| bool | is_edge (Vertex_handle u, Vertex_handle v) const |
Tests whether (u,v) is an edge of tds. | |
| bool | is_facet (Cell_handle c, int i) const |
Tests whether (c,i) is a facet of tds. | |
| bool | is_facet (Vertex_handle u, Vertex_handle v, Vertex_handle w, Cell_handle &c, int &i, int &j, int &k) const |
Tests whether (u,v,w) is a facet of tds. | |
| bool | is_cell (Cell_handle c) const |
Tests whether c is a cell of tds. | |
| bool | is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle t, Cell_handle &c, int &i, int &j, int &k, int &l) const |
Tests whether (u,v,w,t) is a cell of tds. | |
has_vertex | |
There is a method The analogous methods for facets are defined here. | |
| bool | has_vertex (const Facet &f, Vertex_handle v, int &j) const |
If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true. | |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v, int &j) const |
Same for facet (c,i). | |
| bool | has_vertex (const Facet &f, Vertex_handle v) const |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v) const |
| Same as the first two methods, but these two methods do not return the index of the vertex. | |
Equality Tests | |
The following three methods test whether two facets have the same vertices. | |
| bool | are_equal (const Facet &f, const Facet &g) const |
| bool | are_equal (Cell_handle c, int i, Cell_handle n, int j) const |
| bool | are_equal (const Facet &f, Cell_handle n, int j) const |
| For these three methods: | |
Flips | |
Two kinds of flips exist for a three-dimensional triangulation. They are reciprocal. To be flipped, an edge must be incident to three tetrahedra. During the flip, these three tetrahedra disappear and two tetrahedra appear. Figure TDS3figflips (left) shows the edge that is flipped as bold dashed, and one of its three incident facets is shaded. On the right, the facet shared by the two new tetrahedra is shaded. 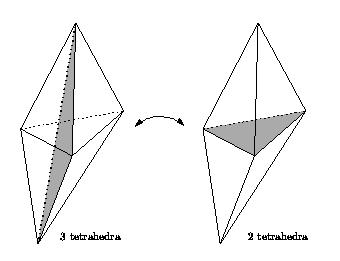
Flips. The following methods guarantee the validity of the resulting 3D combinatorial triangulation. Moreover the flip operations do not invalidate the vertex handles, and only invalidate the cell handles of the affected cells. Flips for a 2d triangulation are not implemented yet | |
| bool | flip (Edge e) |
| bool | flip (Cell_handle c, int i, int j) |
Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive). | |
| void | flip_flippable (Edge e) |
| void | flip_flippable (Cell_handle c, int i, int j) |
| Should be preferred to the previous methods when the edge is known to be flippable. | |
| bool | flip (Facet f) |
| bool | flip (Cell_handle c, int i) |
Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive). | |
| void | flip_flippable (Facet f) |
| void | flip_flippable (Cell_handle c, int i) |
| Should be preferred to the previous methods when the facet is known to be flippable. | |
Insertions | |
The following modifier member functions guarantee the combinatorial validity of the resulting triangulation. | |
| Vertex_handle | insert_in_cell (Cell_handle c) |
Creates a new vertex, inserts it in cell c and returns its handle. | |
| Vertex_handle | insert_in_facet (const Facet &f) |
Creates a new vertex, inserts it in facet f and returns its handle. | |
| Vertex_handle | insert_in_facet (Cell_handle c, int i) |
Creates a new vertex, inserts it in facet i of c and returns its handle. | |
| Vertex_handle | insert_in_edge (Edge e) |
Creates a new vertex, inserts it in edge e and returns its handle. | |
| Vertex_handle | insert_in_edge (Cell_handle c, int i, int j) |
Creates a new vertex, inserts it in edge \( (i,j)\) of c and returns its handle. | |
| Vertex_handle | insert_increase_dimension (Vertex_handle star=Vertex_handle()) |
Transforms a triangulation of the sphere \( S^d\) of \( \mathbb{R}^{d+1}\) into the triangulation of the sphere \( S^{d+1}\) of \( \mathbb{R}^{d+2}\) by adding a new vertex v: v is linked to all the vertices to triangulate one of the two half-spheres of dimension \( (d+1)\). | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i) |
| Creates a new vertex by starring a hole. | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i, Vertex_handle newv) |
Same as above, except that newv will be used as the new vertex, which must have been allocated previously with e.g. | |
Removal | |
| void | remove_decrease_dimension (Vertex_handle v, Vertex_handle w=v) |
This operation is the reciprocal of insert_increase_dimension(). | |
| Cell_handle | remove_from_maximal_dimension_simplex (Vertex_handle v) |
Removes v. | |
Dimension Manipulation | |
The following operation, | |
| void | decrease_dimension (Cell_handle c, int i) |
| The link of a vertex \( v\) is formed by the facets disjoint from \( v\) that are included in the cells incident to \( v\). | |
Other modifiers | |
The following modifiers can affect the validity of the triangulation data structure. | |
| void | reorient () |
| This is an advanced function. | |
| Vertex_handle | create_vertex (const Vertex &v=Vertex()) |
| This is an advanced function. | |
| Vertex_handle | create_vertex (Vertex_handle v) |
| This is an advanced function. | |
| Cell_handle | create_cell (const Cell &c=Cell()) |
| This is an advanced function. | |
| Cell_handle | create_cell (Cell_handle c) |
| This is an advanced function. | |
| Cell_handle | create_cell (Vertex_handle v0, Vertex_handle v1, Vertex_handle v2, Vertex_handle v3) |
| This is an advanced function. | |
| Cell_handle | create_cell (Vertex_handle v0, Vertex_handle v1, Vertex_handle v2, Vertex_handle v3, Cell_handle n0, Cell_handle n1, Cell_handle n2, Cell_handle n3) |
| This is an advanced function. | |
| void | delete_vertex (Vertex_handle v) |
| This is an advanced function. | |
| void | delete_cell (Cell_handle c) |
| This is an advanced function. | |
| template<class VertexIt > | |
| void | delete_vertices (VertexIt first, VertexIt last) |
| This is an advanced function. | |
| template<class CellIt > | |
| void | delete_cells (CellIt first, CellIt last) |
| This is an advanced function. | |
Traversing the triangulation | |
| Cell_iterator | cells_begin () const |
Returns cells_end() when tds.dimension() \( <3\). | |
| Cell_iterator | cells_end () const |
| Cell_iterator | raw_cells_begin () const |
Low-level access to the cells, does not return cells_end() when tds.dimension() \( <3\). | |
| Cell_iterator | raw_cells_end () const |
| Facet_iterator | facets_begin () const |
Returns facets_end() when tds.dimension() \( <2\). | |
| Facet_iterator | facets_end () const |
| Edge_iterator | edges_begin () const |
Returns edges_end() when tds.dimension() \( <1\). | |
| Edge_iterator | edges_end () const |
| Vertex_iterator | vertices_begin () const |
| Vertex_iterator | vertices_end () const |
Cell and facet circulators | |
| Cell_circulator | incident_cells (const Edge &e) const |
Starts at an arbitrary cell incident to e. | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Cell_circulator | incident_cells (const Edge &e, Cell_handle start) const |
Starts at cell start. | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j, Cell_handle start) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Edge e) const |
Starts at an arbitrary facet incident to e. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Edge e, Facet start) const |
Starts at facet start. | |
| Facet_circulator | incident_facets (Edge e, Cell_handle start, int f) const |
Starts at facet of index f in start. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Facet start) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Cell_handle start, int f) const |
As above for edge (i,j) of c and facet (start,f). | |
Traversal of the incident cells, facets and edges, and the adjacent vertices of a given vertex | |
| template<class OutputIterator > | |
| OutputIterator | incident_cells (Vertex_handle v, OutputIterator cells) const |
Copies the Cell_handles of all cells incident to v to the output iterator cells. | |
| template<class OutputIterator > | |
| OutputIterator | incident_facets (Vertex_handle v, OutputIterator facets) const |
Copies the Facets incident to v to the output iterator facets. | |
| template<class OutputIterator > | |
| OutputIterator | incident_edges (Vertex_handle v, OutputIterator edges) const |
Copies all Edges incident to v to the output iterator edges. | |
| template<class OutputIterator > | |
| OutputIterator | adjacent_vertices (Vertex_handle v, OutputIterator vertices) const |
Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices. | |
| size_type | degree (Vertex_handle v) const |
| Returns the degree of a vertex, that is, the number of incident vertices. | |
Traversal between adjacent cells | |
| int | mirror_index (Cell_handle c, int i) const |
Returns the index of c in its \( i^{th}\) neighbor. | |
| Vertex_handle | mirror_vertex (Cell_handle c, int i) const |
Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c. | |
| Facet | mirror_facet (Facet f) const |
| Returns the same facet seen from the other adjacent cell. | |
Checking | |
| bool | is_valid (bool verbose=false) const |
| This is a function for debugging purpose. | |
| bool | is_valid (Vertex_handle v, bool verbose=false) const |
| This is a function for debugging purpose. | |
| bool | is_valid (Cell_handle c, bool verbose=false) const |
| This is a function for debugging purpose. | |
I/O | |
| istream & | operator>> (istream &is, TriangulationDataStructure_3 &tds) |
Reads a combinatorial triangulation from is and assigns it to tds | |
| ostream & | operator<< (ostream &os, const TriangulationDataStructure_3 &tds) |
Writes tds into the stream os | |
| template<typename TDS_src , typename ConvertVertex , typename ConvertCell > | |
| std::istream & | file_input (std::istream &is, ConvertVertex convert_vertex, ConvertCell convert_cell) |
The tds streamed in is, of original type TDS_src, is written into the triangulation data structure. | |
Can be CGAL::Sequential_tag, CGAL::Parallel_tag, or Parallel_if_available_tag.
If it is CGAL::Parallel_tag, the following functions can be called concurrently: create_vertex, create_cell, delete_vertex, delete_cell.
| typedef Triple<Cell_handle, int, int> TriangulationDataStructure_3::Edge |
(c,i,j) is the edge of cell c whose vertices indices are i and j.
(See Section Representation.)
| typedef std::pair<Cell_handle, int> TriangulationDataStructure_3::Facet |
(c,i) is the facet of c opposite to the vertex of index i.
(See Section Representation.)
| using TriangulationDataStructure_3::Rebind_cell = unspecified_type |
This is an advanced type.
This template class allows to get the type of a triangulation data structure that only changes the cell type. It has to define a type Rebind_cell<Cb2>::Other which is a rebound triangulation data structure, that is, the one whose TriangulationDSCellBase_3 will be Cb2.
| using TriangulationDataStructure_3::Rebind_vertex = unspecified_type |
This is an advanced type.
This template class allows to get the type of a triangulation data structure that only changes the vertex type. It has to define a type Rebind_vertex<Vb2>::Other which is a rebound triangulation data structure, that is, the one whose TriangulationDSVertexBase_3 will be Vb2.
| TriangulationDataStructure_3::TriangulationDataStructure_3 | ( | const TriangulationDataStructure_3 & | tds1 | ) |
Copy constructor.
All vertices and cells are duplicated.
| OutputIterator TriangulationDataStructure_3::adjacent_vertices | ( | Vertex_handle | v, |
| OutputIterator | vertices | ||
| ) | const |
Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices.
If tds.dimension() \( <0\), then do nothing. Returns the resulting output iterator.
v \( \neq\) Vertex_handle(), tds.is_vertex(v). | bool TriangulationDataStructure_3::are_equal | ( | const Facet & | f, |
| Cell_handle | n, | ||
| int | j | ||
| ) | const |
For these three methods:
tds.dimension()=3. | void TriangulationDataStructure_3::clear | ( | ) |
Deletes all cells and vertices.
tds is reset as a triangulation data structure constructed by the default constructor.
| Vertex_handle tds TriangulationDataStructure_3::copy_tds | ( | const TDS_src & | tds_src, |
| typename TDS_src::Vertex_handle | v, | ||
| const ConvertVertex & | convert_vertex, | ||
| const ConvertCell & | convert_cell | ||
| ) |
tds_src is copied into this.
As the vertex and cell types might be different and incompatible, the creation of new cells and vertices is made thanks to the functors convert_vertex and convert_cell, that convert vertex and cell types. For each vertex v_src in tds_src, the corresponding vertex v_tgt in this is a copy of the vertex returned by convert_vertex(v_src). The same operations are done for cells with the functor convert_cell. If v != TDS_src::Vertex_handle(), a handle to the vertex created in this that is the copy of v is returned, otherwise Vertex_handle() is returned.
ConvertVertex must provide two operator()'s that are responsible for converting the source vertex v_src into the target vertex:
c_src into the target cell:
v is a vertex of tds_src or is Vertex_handle(). | Vertex_handle TriangulationDataStructure_3::copy_tds | ( | const TriangulationDataStructure_3 & | tds1, |
| Vertex_handle | v = Vertex_handle() |
||
| ) |
tds1 is copied into tds.
If v != Vertex_handle(), the vertex of tds corresponding to v is returned, otherwise Vertex_handle() is returned.
v is a vertex of tds1. | Cell_handle TriangulationDataStructure_3::create_cell | ( | Cell_handle | c | ) |
This is an advanced function.
Creates a cell which is a copy of the one pointed to by c and adds it to the triangulation data structure.
| Cell_handle TriangulationDataStructure_3::create_cell | ( | const Cell & | c = Cell() | ) |
This is an advanced function.
Adds a copy of the cell c to the triangulation data structure.
| Cell_handle TriangulationDataStructure_3::create_cell | ( | Vertex_handle | v0, |
| Vertex_handle | v1, | ||
| Vertex_handle | v2, | ||
| Vertex_handle | v3 | ||
| ) |
This is an advanced function.
Creates a cell and adds it into the triangulation data structure. Initializes the vertices of the cell, its neighbor handles being initialized with the default constructed handle.
| Cell_handle TriangulationDataStructure_3::create_cell | ( | Vertex_handle | v0, |
| Vertex_handle | v1, | ||
| Vertex_handle | v2, | ||
| Vertex_handle | v3, | ||
| Cell_handle | n0, | ||
| Cell_handle | n1, | ||
| Cell_handle | n2, | ||
| Cell_handle | n3 | ||
| ) |
This is an advanced function.
Creates a cell, initializes its vertices and neighbors, and adds it into the triangulation data structure.
| Vertex_handle TriangulationDataStructure_3::create_vertex | ( | const Vertex & | v = Vertex() | ) |
This is an advanced function.
Adds a copy of the vertex v to the triangulation data structure.
| Vertex_handle TriangulationDataStructure_3::create_vertex | ( | Vertex_handle | v | ) |
This is an advanced function.
Creates a vertex which is a copy of the one pointed to by v and adds it to the triangulation data structure.
| void TriangulationDataStructure_3::decrease_dimension | ( | Cell_handle | c, |
| int | i | ||
| ) |
The link of a vertex \( v\) is formed by the facets disjoint from \( v\) that are included in the cells incident to \( v\).
When the link of v = c->vertex(i) contains all the other vertices, decrease_dimension crushes the triangulation of the sphere \( S^d\) of \( \mathbb{R}^{d+1}\) onto the triangulation of the sphere \( S^{d-1}\) of \( \mathbb{R}^{d}\) formed by the link of v augmented with the vertex v itself, for \( d\)==2,3; this one is placed on the facet (c, i) (see Fig. TDS3dim_down).
v must be equal to the total number of vertices of the triangulation data structure minus 1.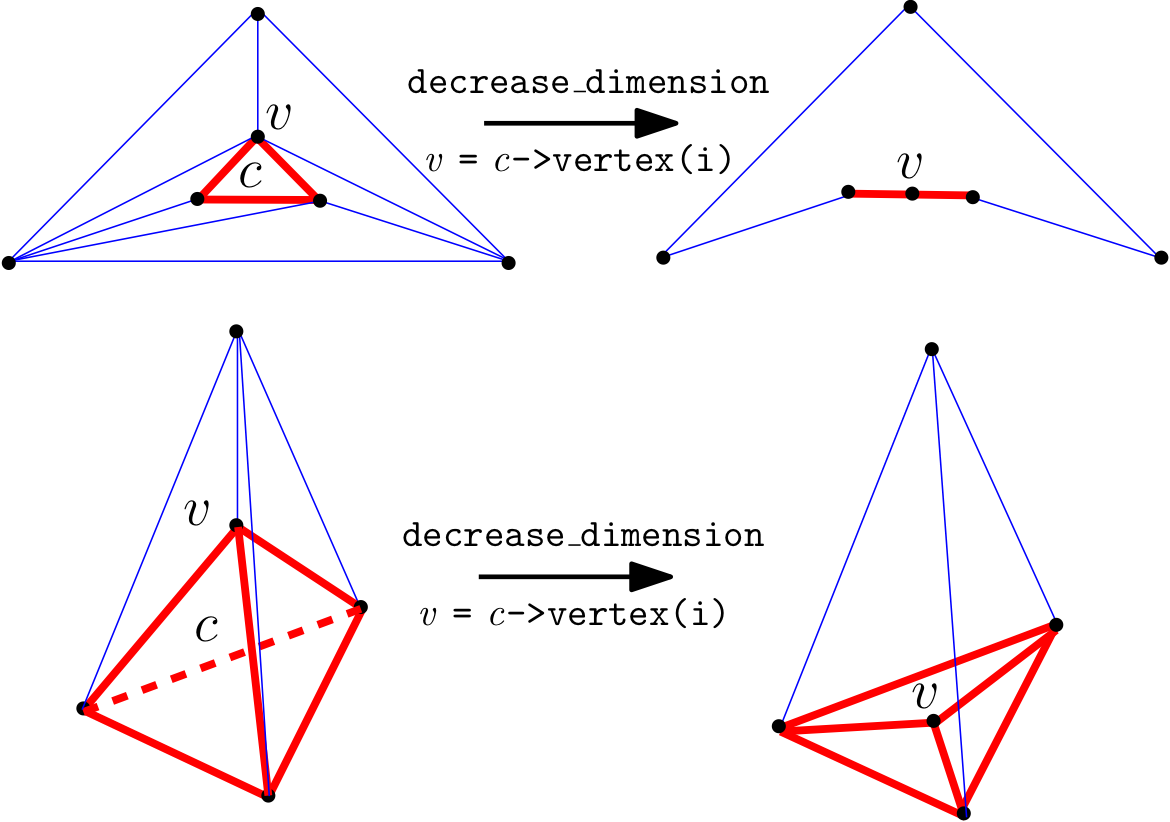
| size_type TriangulationDataStructure_3::degree | ( | Vertex_handle | v | ) | const |
Returns the degree of a vertex, that is, the number of incident vertices.
v \( \neq\) Vertex_handle(), tds.is_vertex(v). | void TriangulationDataStructure_3::delete_cell | ( | Cell_handle | c | ) |
This is an advanced function.
Removes the cell from the triangulation data structure.
tds. | void TriangulationDataStructure_3::delete_cells | ( | CellIt | first, |
| CellIt | last | ||
| ) |
This is an advanced function.
Calls delete_cell over an iterator range of value type Cell_handle.
| void TriangulationDataStructure_3::delete_vertex | ( | Vertex_handle | v | ) |
This is an advanced function.
Removes the vertex from the triangulation data structure.
tds. | void TriangulationDataStructure_3::delete_vertices | ( | VertexIt | first, |
| VertexIt | last | ||
| ) |
This is an advanced function.
Calls delete_vertex over an iterator range of value type Vertex_handle.
| bool TriangulationDataStructure_3::flip | ( | Cell_handle | c, |
| int | i | ||
| ) |
Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive).
They return false or true according to this test.
| bool TriangulationDataStructure_3::flip | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) |
Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive).
They return false or true according to this test.
| void TriangulationDataStructure_3::flip_flippable | ( | Cell_handle | c, |
| int | i | ||
| ) |
Should be preferred to the previous methods when the facet is known to be flippable.
| void TriangulationDataStructure_3::flip_flippable | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) |
Should be preferred to the previous methods when the edge is known to be flippable.
| bool TriangulationDataStructure_3::has_vertex | ( | Cell_handle | c, |
| int | i, | ||
| Vertex_handle | v, | ||
| int & | j | ||
| ) | const |
Same for facet (c,i).
Computes the index j of v in c.
| bool TriangulationDataStructure_3::has_vertex | ( | const Facet & | f, |
| Vertex_handle | v, | ||
| int & | j | ||
| ) | const |
If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true.
tds.dimension()=3 | Cell_circulator TriangulationDataStructure_3::incident_cells | ( | const Edge & | e | ) | const |
Starts at an arbitrary cell incident to e.
tds.dimension() \( =3\) | Cell_circulator TriangulationDataStructure_3::incident_cells | ( | const Edge & | e, |
| Cell_handle | start | ||
| ) | const |
Starts at cell start.
tds.dimension() \( =3\) and start is incident to e. | OutputIterator TriangulationDataStructure_3::incident_cells | ( | Vertex_handle | v, |
| OutputIterator | cells | ||
| ) | const |
Copies the Cell_handles of all cells incident to v to the output iterator cells.
Returns the resulting output iterator.
tds.dimension() \( =3\), v \( \neq\) Vertex_handle(), tds.is_vertex(v). | OutputIterator TriangulationDataStructure_3::incident_edges | ( | Vertex_handle | v, |
| OutputIterator | edges | ||
| ) | const |
Copies all Edges incident to v to the output iterator edges.
Returns the resulting output iterator.
tds.dimension() \( >0\), v \( \neq\) Vertex_handle(), tds.is_vertex(v). | Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) | const |
As above for edge (i,j) of c.
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
| Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Cell_handle | c, |
| int | i, | ||
| int | j, | ||
| Cell_handle | start, | ||
| int | f | ||
| ) | const |
As above for edge (i,j) of c and facet (start,f).
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
| Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Cell_handle | c, |
| int | i, | ||
| int | j, | ||
| Facet | start | ||
| ) | const |
As above for edge (i,j) of c.
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
| Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Edge | e | ) | const |
Starts at an arbitrary facet incident to e.
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
tds.dimension() \( =3\) | Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Edge | e, |
| Cell_handle | start, | ||
| int | f | ||
| ) | const |
Starts at facet of index f in start.
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
| Facet_circulator TriangulationDataStructure_3::incident_facets | ( | Edge | e, |
| Facet | start | ||
| ) | const |
Starts at facet start.
Only defined in dimension 3, though are defined also in dimension 2: there are only two facets sahring an edge in dimension 2.
start is incident to e. | OutputIterator TriangulationDataStructure_3::incident_facets | ( | Vertex_handle | v, |
| OutputIterator | facets | ||
| ) | const |
Copies the Facets incident to v to the output iterator facets.
Returns the resulting output iterator.
tds.dimension() \( >1\), v \( \neq\) Vertex_handle(), tds.is_vertex(v). | Vertex_handle TriangulationDataStructure_3::insert_in_cell | ( | Cell_handle | c | ) |
Creates a new vertex, inserts it in cell c and returns its handle.
The cell c is split into four new cells, each of these cells being formed by the new vertex and a facet of c.
tds.dimension() \( = 3\) and c is a cell of tds. | Vertex_handle TriangulationDataStructure_3::insert_in_edge | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) |
Creates a new vertex, inserts it in edge \( (i,j)\) of c and returns its handle.
tds.dimension() \( \geq1\). \( i\neq j\), \( i,j \in\{0,1,2,3\}\) in dimension 3, \( i,j \in\{0,1,2\}\) in dimension 2, \( i,j \in\{0,1\}\) in dimension 1 and (c,i,j) is an edge of tds. | Vertex_handle TriangulationDataStructure_3::insert_in_edge | ( | Edge | e | ) |
Creates a new vertex, inserts it in edge e and returns its handle.
In dimension 3, all the incident cells are split into 2 new cells; in dimension 2, the 2 incident facets are split into 2 new facets; in dimension 1, the edge is split into 2 new edges.
tds.dimension() \( \geq1\) and e is an edge of tds. | Vertex_handle TriangulationDataStructure_3::insert_in_facet | ( | Cell_handle | c, |
| int | i | ||
| ) |
Creates a new vertex, inserts it in facet i of c and returns its handle.
tds.dimension() \( \geq2\), \( i \in\{0,1,2,3\}\) in dimension 3, \( i=3\) in dimension 2 and (c,i) is a facet of tds. | Vertex_handle TriangulationDataStructure_3::insert_in_facet | ( | const Facet & | f | ) |
Creates a new vertex, inserts it in facet f and returns its handle.
In dimension 3, the two incident cells are split into 3 new cells; in dimension 2, the facet is split into 3 facets.
tds.dimension() \( \geq2\) and f is a facet of tds. | Vertex_handle TriangulationDataStructure_3::insert_in_hole | ( | CellIt | cell_begin, |
| CellIt | cell_end, | ||
| Cell_handle | begin, | ||
| int | i | ||
| ) |
Creates a new vertex by starring a hole.
It takes an iterator range [cell_begin; cell_end[ of Cell_handles which specifies a set of connected cells (resp. facets in dimension 2) describing a hole. (begin, i) is a facet (resp. an edge) on the boundary of the hole, that is, begin belongs to the set of cells (resp. facets) previously described, and begin->neighbor(i) does not. Then this function deletes all the cells (resp. facets) describing the hole, creates a new vertex v, and for each facet (resp. edge) on the boundary of the hole, creates a new cell (resp. facet) with v as vertex. v is returned.
tds.dimension() \( \geq2\), the set of cells (resp. facets) is connected, and its boundary is connected. | Vertex_handle TriangulationDataStructure_3::insert_in_hole | ( | CellIt | cell_begin, |
| CellIt | cell_end, | ||
| Cell_handle | begin, | ||
| int | i, | ||
| Vertex_handle | newv | ||
| ) |
Same as above, except that newv will be used as the new vertex, which must have been allocated previously with e.g.
create_vertex.
| Vertex_handle TriangulationDataStructure_3::insert_increase_dimension | ( | Vertex_handle | star = Vertex_handle() | ) |
Transforms a triangulation of the sphere \( S^d\) of \( \mathbb{R}^{d+1}\) into the triangulation of the sphere \( S^{d+1}\) of \( \mathbb{R}^{d+2}\) by adding a new vertex v: v is linked to all the vertices to triangulate one of the two half-spheres of dimension \( (d+1)\).
Vertex star is used to triangulate the second half-sphere (when there is an associated geometric triangulation, star is in fact the vertex associated with its infinite vertex). See Figure TDS3figtopoinsert_outside_affine_hull.
The numbering of the cells is such that, if f was a face of maximal dimension in the initial triangulation, then (f,v) (in this order) is the corresponding face in the new triangulation. This method can be used to insert the first two vertices in an empty triangulation.
A handle to v is returned.
tds.dimension() \( = d < 3\). When tds.number_of_vertices() \( >0\), \( star \neq\) Vertex_handle() and star is a vertex of tds.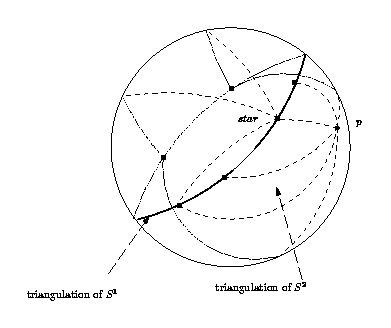
| bool TriangulationDataStructure_3::is_cell | ( | Cell_handle | c | ) | const |
Tests whether c is a cell of tds.
Answers false when dimension() \( <3\) .
| bool TriangulationDataStructure_3::is_cell | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Vertex_handle | w, | ||
| Vertex_handle | t, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j, | ||
| int & | k, | ||
| int & | l | ||
| ) | const |
Tests whether (u,v,w,t) is a cell of tds.
If the cell c is found, it computes the indices i, j, k and l of the vertices u, v, w and t in c, in this order.
| bool TriangulationDataStructure_3::is_edge | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) | const |
Tests whether (c,i,j) is an edge of tds.
Answers false when dimension() \( <1\) .
| bool TriangulationDataStructure_3::is_edge | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j | ||
| ) | const |
Tests whether (u,v) is an edge of tds.
If the edge is found, it computes a cell c having this edge and the indices i and j of the vertices u and v, in this order.
| bool TriangulationDataStructure_3::is_facet | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Tests whether (c,i) is a facet of tds.
Answers false when dimension() \( <2\) .
| bool TriangulationDataStructure_3::is_facet | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Vertex_handle | w, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j, | ||
| int & | k | ||
| ) | const |
Tests whether (u,v,w) is a facet of tds.
If the facet is found, it computes a cell c having this facet and the indices i, j and k of the vertices u, v and w, in this order.
| bool TriangulationDataStructure_3::is_valid | ( | bool | verbose = false | ) | const |
This is a function for debugging purpose.
Checks the combinatorial validity of the triangulation by checking the local validity of all its cells and vertices (see functions below). (See Section Representation.) Moreover, the Euler relation is tested.
When verbose is set to true, messages are printed to give a precise indication on the kind of invalidity encountered.
| bool TriangulationDataStructure_3::is_valid | ( | Cell_handle | c, |
| bool | verbose = false |
||
| ) | const |
This is a function for debugging purpose.
Checks the local validity of the adjacency relations of the triangulation. It also calls the is_valid member function of the cell. When verbose is set to true, messages are printed to give a precise indication on the kind of invalidity encountered.
| bool TriangulationDataStructure_3::is_valid | ( | Vertex_handle | v, |
| bool | verbose = false |
||
| ) | const |
This is a function for debugging purpose.
Checks the local validity of the adjacency relations of the triangulation. It also calls the is_valid member function of the vertex. When verbose is set to true, messages are printed to give a precise indication on the kind of invalidity encountered.
| int TriangulationDataStructure_3::mirror_index | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the index of c in its \( i^{th}\) neighbor.
| Vertex_handle TriangulationDataStructure_3::mirror_vertex | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c.
| size_type TriangulationDataStructure_3::number_of_cells | ( | ) | const |
The number of cells.
Returns 0 if tds.dimension() \( <3\).
| size_type TriangulationDataStructure_3::number_of_edges | ( | ) | const |
The number of edges.
Returns 0 if tds.dimension() \( <1\).
| size_type TriangulationDataStructure_3::number_of_facets | ( | ) | const |
The number of facets.
Returns 0 if tds.dimension() \( <2\).
| size_type TriangulationDataStructure_3::number_of_vertices | ( | ) | const |
The number of vertices.
Note that the triangulation data structure has one more vertex than an associated geometric triangulation, if there is one, since the infinite vertex is a standard vertex and is thus also counted.
| TriangulationDataStructure_3 & TriangulationDataStructure_3::operator= | ( | const TriangulationDataStructure_3 & | tds1 | ) |
Assignment operator.
All vertices and cells are duplicated, and the former data structure of tds is deleted.
| void TriangulationDataStructure_3::remove_decrease_dimension | ( | Vertex_handle | v, |
| Vertex_handle | w = v |
||
| ) |
This operation is the reciprocal of insert_increase_dimension().
It transforms a triangulation of the sphere \( S^d\) of \( \mathbb{R}^{d+1}\) into the triangulation of the sphere \( S^{d-1}\) of \( \mathbb{R}^{d}\) by removing the vertex v. Delete the cells incident to w, keep the others.
tds.dimension() \( = d \geq-1\). tds.degree(v) \( =\) degree(w) \( =\) tds.number_of_vertices() \( -1\). | Cell_handle TriangulationDataStructure_3::remove_from_maximal_dimension_simplex | ( | Vertex_handle | v | ) |
Removes v.
The incident simplices of maximal dimension incident to v are replaced by a single simplex of the same dimension. This operation is exactly the reciprocal to tds.insert_in_cell(v) in dimension 3, tds.insert_in_facet(v) in dimension 2, and tds.insert_in_edge(v) in dimension 1.
tds.degree(v) \( =\) tds.dimension()+1. | void TriangulationDataStructure_3::reorient | ( | ) |
This is an advanced function.
Changes the orientation of all cells of the triangulation data structure.
tds.dimension() \( \geq1\). | void TriangulationDataStructure_3::set_dimension | ( | int | n | ) |
This is an advanced function.
Sets the dimension to n.
| void TriangulationDataStructure_3::swap | ( | TriangulationDataStructure_3 & | tds1 | ) |
Swaps tds and tds1.
There is no copy of cells and vertices, thus this method runs in constant time. This method should be preferred to tds=tds1 or tds(tds1) when tds1 is deleted after that.