|
CGAL 6.1.1 - 3D Triangulations
|
|
CGAL 6.1.1 - 3D Triangulations
|
#include <CGAL/Triangulation_3.h>
Inherited by CGAL::Regular_triangulation_3< Traits, TDS, SLDS >.
The class Triangulation_3 represents a 3-dimensional tetrahedralization of points.
| Traits | is the geometric traits class and must be a model of TriangulationTraits_3. |
| TDS | is the triangulation data structure and must be a model of TriangulationDataStructure_3. Default may be used, with default type Triangulation_data_structure_3<Triangulation_vertex_base_3<Traits>, Triangulation_cell_base_3<Traits> >. Any custom type can be used instead of Triangulation_vertex_base_3 and Triangulation_cell_base_3, provided that they are models of the concepts TriangulationVertexBase_3 and TriangulationCellBase_3, respectively. |
| SLDS | is an optional parameter to specify the type of the spatial lock data structure. It must be a model of the SurjectiveLockDataStructure concept, with object being a Point (as defined below). It is only used if the triangulation data structure used is concurrency-safe (i.e. when TriangulationDataStructure_3::Concurrency_tag is Parallel_tag). The default value is Spatial_lock_grid_3<Tag_priority_blocking> if the triangulation data structure is concurrency-safe, and void otherwise. In order to use concurrent operations, the user must provide a reference to a SLDS instance via the constructor or Triangulation_3::set_lock_data_structure. |
Traversal of the Triangulation
The triangulation class provides several iterators and circulators that allow one to traverse it (completely or partially).
Public Types | |
| enum | Locate_type { VERTEX =0 , EDGE , FACET , CELL , OUTSIDE_CONVEX_HULL , OUTSIDE_AFFINE_HULL } |
The enum Locate_type is defined by Triangulation_3 to specify which case occurs when locating a point in the triangulation. More... | |
Types | |
The class | |
| typedef Traits | Geom_traits |
| typedef TDS | Triangulation_data_structure |
| typedef SLDS | Lock_data_structure |
| typedef Triangulation_data_structure::Vertex::Point | Point |
| typedef Geom_traits::Segment_3 | Segment |
| typedef Geom_traits::Triangle_3 | Triangle |
| typedef Geom_traits::Tetrahedron_3 | Tetrahedron |
Only vertices (0-faces) and cells (3-faces) are stored. Edges (1-faces) and facets (2-faces) are not explicitly represented and thus there are no corresponding classes (see Section Representation). | |
| typedef Triangulation_data_structure::Vertex | Vertex |
| typedef Triangulation_data_structure::Cell | Cell |
| typedef Triangulation_data_structure::Facet | Facet |
| typedef Triangulation_data_structure::Edge | Edge |
| typedef Triangulation_data_structure::Concurrency_tag | Concurrency_tag |
| Concurrency tag (from the TDS). | |
The vertices and faces of the triangulations are accessed through A handle is a model of the | |
| typedef Triangulation_data_structure::Vertex_handle | Vertex_handle |
| handle to a vertex | |
| typedef Triangulation_data_structure::Cell_handle | Cell_handle |
| handle to a cell | |
| typedef Triangulation_simplex_3< Self > | Simplex |
| Reference to a simplex (vertex, edge, facet or cell) of the triangulation. | |
| typedef Triangulation_data_structure::size_type | size_type |
| Size type (an unsigned integral type) | |
| typedef Triangulation_data_structure::difference_type | difference_type |
| Difference type (a signed integral type) | |
| typedef Triangulation_data_structure::Cell_iterator | All_cells_iterator |
| iterator over cells | |
| typedef Triangulation_data_structure::Facet_iterator | All_facets_iterator |
| iterator over facets | |
| typedef Triangulation_data_structure::Edge_iterator | All_edges_iterator |
| iterator over edges | |
| typedef Triangulation_data_structure::Vertex_iterator | All_vertices_iterator |
| iterator over vertices | |
| typedef unspecified_type | Finite_cells_iterator |
| iterator over finite cells | |
| typedef unspecified_type | Finite_facets_iterator |
| iterator over finite facets | |
| typedef unspecified_type | Finite_edges_iterator |
| iterator over finite edges | |
| typedef unspecified_type | Finite_vertices_iterator |
| iterator over finite vertices | |
| typedef unspecified_type | Point_iterator |
| iterator over the points corresponding to the finite vertices of the triangulation. | |
| typedef Triangulation_data_structure::Cell_circulator | Cell_circulator |
| circulator over all cells incident to a given edge | |
| typedef Triangulation_data_structure::Facet_circulator | Facet_circulator |
| circulator over all facets incident to a given edge | |
| typedef unspecified_type | Segment_cell_iterator |
| iterator over cells intersected by a line segment. | |
| typedef unspecified_type | Segment_simplex_iterator |
| iterator over simplices intersected by a line segment. | |
In order to write C++ 11 | |
| typedef Iterator_range< unspecified_type > | All_cell_handles |
range type for iterating over all cell handles (including infinite cells), with a nested type iterator that has as value type Cell_handle. | |
| typedef Iterator_range< All_facets_iterator > | All_facets |
| range type for iterating over facets. | |
| typedef Iterator_range< All_edges_iterator > | All_edges |
| range type for iterating over edges. | |
| typedef Iterator_range< unspecified_type > | All_vertex_handles |
range type for iterating over all vertex handles, with a nested type iterator that has as value type Vertex_handle. | |
| typedef Iterator_range< unspecified_type > | Finite_cell_handles |
range type for iterating over finite cell handles, with a nested type iterator that has as value type Cell_handle. | |
| typedef Iterator_range< Finite_facets_iterator > | Finite_facets |
| range type for iterating over finite facets. | |
| typedef Iterator_range< Finite_edges_iterator > | Finite_edges |
| range type for iterating over finite edges. | |
| typedef Iterator_range< unspecified_type > | Finite_vertex_handles |
range type for iterating over finite vertex handles, with a nested type iterator that has as value type Vertex_handle. | |
| typedef Iterator_range< unspecified_type > | Points |
| range type for iterating over the points of the finite vertices. | |
| typedef Iterator_range< unspecified_type > | Segment_traverser_cell_handles |
| range type for iterating over the cells intersected by a line segment. | |
| typedef Iterator_range< Segment_simplex_iterator > | Segment_traverser_simplices |
| range type for iterating over the simplices intersected by a line segment. | |
Creation | |
| Triangulation_3 (const Geom_traits &traits=Geom_traits(), Lock_data_structure *lock_ds=nullptr) | |
Introduces a triangulation t having only one vertex which is the infinite vertex. | |
| Triangulation_3 (Lock_data_structure *lock_ds=nullptr, const Geom_traits &traits=Geom_traits()) | |
| Same as the previous one, but with parameters in reverse order. | |
| Triangulation_3 (const Triangulation_3 &tr) | |
| Copy constructor. | |
| template<class InputIterator > | |
| Triangulation_3 (InputIterator first, InputIterator last, const Geom_traits &traits=Geom_traits(), Lock_data_structure *lock_ds=nullptr) | |
Equivalent to constructing an empty triangulation with the optional traits class argument and calling insert(first,last). | |
Assignment | |
| Triangulation_3 & | operator= (const Triangulation_3 &tr) |
The triangulation tr is duplicated, and modifying the copy after the duplication does not modify the original. | |
| void | swap (Triangulation_3 &tr) |
The triangulations tr and t are swapped. | |
| void | clear () |
Deletes all finite vertices and all cells of t. | |
| template<class GT , class Tds1 , class Tds2 > | |
| bool | operator== (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2) |
| Equality operator. | |
| template<class GT , class Tds1 , class Tds2 > | |
| bool | operator!= (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2) |
The opposite of operator==. | |
Access Functions | |
| const Geom_traits & | geom_traits () const |
| Returns a const reference to the geometric traits object. | |
| const Triangulation_data_structure & | tds () const |
| Returns a const reference to the triangulation data structure. | |
| Triangulation_data_structure & | tds () |
| Returns a reference to the triangulation data structure. | |
| int | dimension () const |
| Returns the dimension of the affine hull. | |
| size_type | number_of_vertices () const |
| Returns the number of finite vertices. | |
| size_type | number_of_cells () const |
Returns the number of cells or 0 if t.dimension() < 3. | |
| Vertex_handle | infinite_vertex () |
| Returns the infinite vertex. | |
| void | set_infinite_vertex (Vertex_handle v) |
| This is an advanced function. | |
| Cell_handle | infinite_cell () const |
| Returns a cell incident to the infinite vertex. | |
Non-Constant-Time Access Functions | |
As previously said, the triangulation is a collection of cells that are either infinite or represent a finite tetrahedra, where an infinite cell is a cell incident to the infinite vertex. Similarly we call an edge (resp. facet) | |
| size_type | number_of_facets () const |
| The number of facets. | |
| size_type | number_of_edges () const |
| The number of edges. | |
| size_type | number_of_finite_cells () const |
| The number of finite cells. | |
| size_type | number_of_finite_facets () const |
| The number of finite facets. | |
| size_type | number_of_finite_edges () const |
| The number of finite edges. | |
Geometric Access Functions | |
| Tetrahedron | tetrahedron (Cell_handle c) const |
Returns the tetrahedron formed by the four vertices of c. | |
| Triangle | triangle (Cell_handle c, int i) const |
Returns the triangle formed by the three vertices of facet (c,i). | |
| Triangle | triangle (const Facet &f) const |
Same as the previous method for facet f. | |
| Segment | segment (const Edge &e) const |
Returns the line segment formed by the vertices of e. | |
| Segment | segment (Cell_handle c, int i, int j) const |
Same as the previous method for edge (c,i,j). | |
| const Point & | point (Cell_handle c, int i) const |
Returns the point given by vertex i of cell c. | |
| const Point & | point (Vertex_handle v) const |
Same as the previous method for vertex v. | |
Tests for Finite and Infinite Vertices and Faces | |
| bool | is_infinite (Vertex_handle v) const |
true, iff vertex v is the infinite vertex. | |
| bool | is_infinite (Cell_handle c) const |
true, iff c is incident to the infinite vertex. | |
| bool | is_infinite (Cell_handle c, int i) const |
true, iff the facet i of cell c is incident to the infinite vertex. | |
| bool | is_infinite (const Facet &f) const |
true iff facet f is incident to the infinite vertex. | |
| bool | is_infinite (Cell_handle c, int i, int j) const |
true, iff the edge (i,j) of cell c is incident to the infinite vertex. | |
| bool | is_infinite (const Edge &e) const |
true iff edge e is incident to the infinite vertex. | |
Queries | |
| bool | is_vertex (const Point &p, Vertex_handle &v) const |
Tests whether p is a vertex of t by locating p in the triangulation. | |
| bool | is_vertex (Vertex_handle v) const |
Tests whether v is a vertex of t. | |
| bool | is_edge (Vertex_handle u, Vertex_handle v, Cell_handle &c, int &i, int &j) const |
Tests whether (u,v) is an edge of t. | |
| bool | is_facet (Vertex_handle u, Vertex_handle v, Vertex_handle w, Cell_handle &c, int &i, int &j, int &k) const |
Tests whether (u,v,w) is a facet of t. | |
| bool | is_cell (Cell_handle c) const |
Tests whether c is a cell of t. | |
| bool | is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c, int &i, int &j, int &k, int &l) const |
Tests whether (u,v,w,x) is a cell of t. | |
| bool | is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c) const |
Tests whether (u,v,w,x) is a cell of t and computes this cell c. | |
There is a method The analogous methods for facets are defined here. | |
| bool | has_vertex (const Facet &f, Vertex_handle v, int &j) const |
If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true. | |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v, int &j) const |
Same for facet (c,i). | |
| bool | has_vertex (const Facet &f, Vertex_handle v) const |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v) const |
| Same as the first two methods, but these two methods do not return the index of the vertex. | |
The following three methods test whether two facets have the same vertices. | |
| bool | are_equal (Cell_handle c, int i, Cell_handle n, int j) const |
| bool | are_equal (const Facet &f, const Facet &g) const |
| bool | are_equal (const Facet &f, Cell_handle n, int j) const |
| For these three methods: | |
Point Location | |
The class It provides also functions to test if a given point is inside a finite face or not. Note that the class | |
| Cell_handle | locate (const Point &query, Cell_handle start=Cell_handle(), bool *could_lock_zone=nullptr) const |
If the point query lies inside the convex hull of the points, the cell that contains the query in its interior is returned. | |
| Cell_handle | locate (const Point &query, Vertex_handle hint, bool *could_lock_zone=nullptr) const |
Same as above but uses hint as the starting place for the search. | |
| Cell_handle | inexact_locate (const Point &query, Cell_handle start=Cell_handle()) const |
Same as locate() but uses inexact predicates. | |
| Cell_handle | locate (const Point &query, Locate_type <, int &li, int &lj, Cell_handle start=Cell_handle(), bool *could_lock_zone=nullptr) const |
If query lies inside the affine hull of the points, the \( k\)-face (finite or infinite) that contains query in its interior is returned, by means of the cell returned together with lt, which is set to the locate type of the query (VERTEX, EDGE, FACET, CELL, or OUTSIDE_CONVEX_HULL if the cell is infinite and query lies strictly in it) and two indices li and lj that specify the \( k\)-face of the cell containing query. | |
| Cell_handle | locate (const Point &query, Locate_type <, int &li, int &lj, Vertex_handle hint, bool *could_lock_zone=nullptr) const |
Same as above but uses hint as the starting place for the search. | |
| Bounded_side | side_of_cell (const Point &p, Cell_handle c, Locate_type <, int &li, int &lj) const |
Returns a value indicating on which side of the oriented boundary of c the point p lies. | |
| Bounded_side | side_of_facet (const Point &p, const Facet &f, Locate_type <, int &li, int &lj) const |
Returns a value indicating on which side of the oriented boundary of f the point p lies: | |
| Bounded_side | side_of_facet (const Point &p, Cell_handle c, Locate_type <, int &li, int &lj) const |
Same as the previous method for the facet (c,3). | |
| Bounded_side | side_of_edge (const Point &p, const Edge &e, Locate_type <, int &li) const |
Returns a value indicating on which side of the oriented boundary of e the point p lies: | |
| Bounded_side | side_of_edge (const Point &p, Cell_handle c, Locate_type <, int &li) const |
| Same as the previous method for edge \( (c,0,1)\). | |
Flips | |
Two kinds of flips exist for a three-dimensional triangulation. They are reciprocal. To be flipped, an edge must be incident to three tetrahedra. During the flip, these three tetrahedra disappear and two tetrahedra appear. Figure 48.1 (left) shows the edge that is flipped as bold dashed, and one of its three incident facets is shaded. On the right, the facet shared by the two new tetrahedra is shaded. Flips are possible only under the following conditions: - the edge or facet to be flipped is not on the boundary of the convex hull of the triangulation - the five points involved are in convex position. 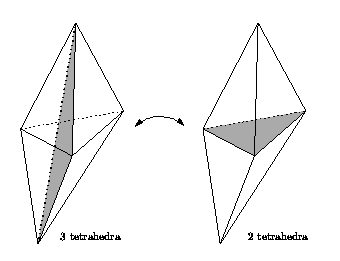
Figure 48.1 Flips The following methods guarantee the validity of the resulting 3D triangulation. Flips for a 2d triangulation are not implemented yet. | |
| bool | flip (Edge e) |
| bool | flip (Cell_handle c, int i, int j) |
Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive). | |
| void | flip_flippable (Edge e) |
| void | flip_flippable (Cell_handle c, int i, int j) |
| Should be preferred to the previous methods when the edge is known to be flippable. | |
| bool | flip (Facet f) |
| bool | flip (Cell_handle c, int i) |
Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive). | |
| void | flip_flippable (Facet f) |
| void | flip_flippable (Cell_handle c, int i) |
| Should be preferred to the previous methods when the facet is known to be flippable. | |
Insertions | |
The following operations are guaranteed to lead to a valid triangulation when they are applied on a valid triangulation. | |
| Vertex_handle | insert (const Point &p, Cell_handle start=Cell_handle()) |
Inserts the point p in the triangulation and returns the corresponding vertex. | |
| Vertex_handle | insert (const Point &p, Vertex_handle hint) |
Same as above but uses hint as the starting place for the search. | |
| Vertex_handle | insert (const Point &p, Locate_type lt, Cell_handle loc, int li, int lj) |
Inserts the point p in the triangulation and returns the corresponding vertex. | |
| template<class PointInputIterator > | |
| std::ptrdiff_t | insert (PointInputIterator first, PointInputIterator last) |
Inserts the points in the range [first,last) in the given order, and returns the number of inserted points. | |
| template<class PointWithInfoInputIterator > | |
| std::ptrdiff_t | insert (PointWithInfoInputIterator first, PointWithInfoInputIterator last) |
Inserts the points in the iterator range [first,last) in the given order, and returns the number of inserted points. | |
We also provide some other methods that can be used instead of They are also guaranteed to lead to a valid triangulation when they are applied on a valid triangulation. | |
| Vertex_handle | insert_in_cell (const Point &p, Cell_handle c) |
Inserts the point p in the cell c. | |
| Vertex_handle | insert_in_facet (const Point &p, const Facet &f) |
Inserts the point p in the facet f. | |
| Vertex_handle | insert_in_facet (const Point &p, Cell_handle c, int i) |
As above, insertion in the facet (c,i). | |
| Vertex_handle | insert_in_edge (const Point &p, const Edge &e) |
Inserts p in the edge e. | |
| Vertex_handle | insert_in_edge (const Point &p, Cell_handle c, int i, int j) |
As above, inserts p in the edge \( (i, j)\) of c. | |
| Vertex_handle | insert_outside_convex_hull (const Point &p, Cell_handle c) |
The cell c must be an infinite cell containing p. | |
| Vertex_handle | insert_outside_affine_hull (const Point &p) |
p is linked to all the points, and the infinite vertex is linked to all the points (including p) to triangulate the new infinite face, so that all the points now belong to the boundary of the convex hull. | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (const Point &p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i) |
| Creates a new vertex by starring a hole. | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (const Point &p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i, Vertex_handle newv) |
Same as above, except that newv will be used as the new vertex, which must have been allocated previously with e.g. create_vertex. | |
Cell, Face, Edge and Vertex Iterators | |
The following iterators allow the user to visit cells, facets, edges and vertices of the triangulation. These iterators are non-mutable, bidirectional and their value types are respectively | |
| Finite_vertices_iterator | finite_vertices_begin () const |
| Starts at an arbitrary finite vertex. | |
| Finite_vertices_iterator | finite_vertices_end () const |
| Past-the-end iterator. | |
| Finite_edges_iterator | finite_edges_begin () const |
| Starts at an arbitrary finite edge. | |
| Finite_edges_iterator | finite_edges_end () const |
| Past-the-end iterator. | |
| Finite_facets_iterator | finite_facets_begin () const |
| Starts at an arbitrary finite facet. | |
| Finite_facets_iterator | finite_facets_end () const |
| Past-the-end iterator. | |
| Finite_cells_iterator | finite_cells_begin () const |
| Starts at an arbitrary finite cell. | |
| Finite_cells_iterator | finite_cells_end () const |
| Past-the-end iterator. | |
| All_vertices_iterator | all_vertices_begin () const |
| Starts at an arbitrary vertex. | |
| All_vertices_iterator | all_vertices_end () const |
| Past-the-end iterator. | |
| All_edges_iterator | all_edges_begin () const |
| Starts at an arbitrary edge. | |
| All_edges_iterator | all_edges_end () const |
| Past-the-end iterator. | |
| All_facets_iterator | all_facets_begin () const |
| Starts at an arbitrary facet. | |
| All_facets_iterator | all_facets_end () const |
| Past-the-end iterator. | |
| All_cells_iterator | all_cells_begin () const |
| Starts at an arbitrary cell. | |
| All_cells_iterator | all_cells_end () const |
| Past-the-end iterator. | |
| Point_iterator | points_begin () const |
| Iterates over the points of the triangulation. | |
| Point_iterator | points_end () const |
| Past-the-end iterator. | |
Ranges | |
In order to write C++ 11 Note that vertex and cell ranges are special. See Section Iterators and Ranges in the User Manual. | |
| All_cell_handles | all_cell_handles () const |
| returns a range of iterators over all cells (even the infinite cells). | |
| All_facets | all_facets () const |
| returns a range of iterators starting at an arbitrary facet. | |
| All_edges | all_edges () const |
| returns a range of iterators starting at an arbitrary edge. | |
| All_vertex_handles | all_vertex_handles () const |
| returns a range of iterators over all vertices (even the infinite one). | |
| Finite_cell_handles | finite_cell_handles () const |
| returns a range of iterators over finite cells. | |
| Finite_facets | finite_facets () const |
| returns a range of iterators starting at an arbitrary facet. | |
| Finite_edges | finite_edges () const |
| returns a range of iterators starting at an arbitrary edge. | |
| Finite_vertex_handles | finite_vertex_handles () const |
| returns a range of iterators over finite vertices. | |
| Points | points () const |
| returns a range of iterators over the points of finite vertices. | |
| std::array< Vertex_handle, 2 > | vertices (const Edge &e) const |
returns an array containing the vertices of e, in the order of their indices e.second and e.third in the cell e.first. | |
| std::array< Vertex_handle, 3 > | vertices (const Facet &f) const |
returns an array containing the vertices of f, in counterclockwise order on the face of f.first opposite to vertex f.first->vertex(f.second). | |
| std::array< Vertex_handle, 4 > | vertices (const Cell_handle c) const |
returns an array containing the vertices of c, in the same order as the indices in c. | |
| Segment_traverser_cell_handles | segment_traverser_cell_handles () const |
| returns a range of iterators over the cells intersected by a line segment | |
| Segment_traverser_simplices | segment_traverser_simplices () const |
| returns a range of iterators over the simplices intersected by a line segment | |
Segment Cell Iterator | |
The triangulation defines an iterator that visits cells intersected by a line segment. Segment Cell Iterator iterates over a sequence of cells which union contains the segment The cells visited form a facet-connected region containing both source and target points of the line segment
Note that for categories 4 and 6, it is not predetermined which incident cells are visited. However, exactly two of the incident cells
Its | |
| Segment_cell_iterator | segment_traverser_cells_begin (Vertex_handle vs, Vertex_handle vt) const |
returns the iterator that allows to visit the cells intersected by the line segment [vs,vt]. | |
| Segment_cell_iterator | segment_traverser_cells_begin (const Point &ps, const Point &pt, Cell_handle hint=Cell_handle()) const |
returns the iterator that allows to visit the cells intersected by the line segment [ps, pt]. | |
| Segment_cell_iterator | segment_traverser_cells_end () const |
| returns the past-the-end iterator over the intersected cells. | |
Segment Simplex Iterator | |
The triangulation defines an iterator that visits all the triangulation simplices (vertices, edges, facets and cells) intersected by a line segment. The iterator traverses a connected sequence of simplices - possibly of all dimensions - intersected by the line segment Each simplex falls within one or more of the following categories:
Its | |
| Segment_simplex_iterator | segment_traverser_simplices_begin (Vertex_handle vs, Vertex_handle vt) const |
returns the iterator that allows to visit the simplices intersected by the line segment [vs,vt]. | |
| Segment_simplex_iterator | segment_traverser_simplices_begin (const Point &ps, const Point &pt, Cell_handle hint=Cell_handle()) const |
returns the iterator that allows to visit the simplices intersected by the line segment [ps,pt]. | |
| Segment_simplex_iterator | segment_traverser_simplices_end () const |
| returns the past-the-end iterator over the intersected simplices. | |
Cell and Facet Circulators | |
The following circulators respectively visit all cells or all facets incident to a given edge. They are non-mutable and bidirectional. They are invalidated by any modification of one of the cells traversed. | |
| Cell_circulator | incident_cells (Edge e) const |
Starts at an arbitrary cell incident to e. | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Cell_circulator | incident_cells (Edge e, Cell_handle start) const |
Starts at cell start. | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j, Cell_handle start) const |
As above for edge (i,j) of c. | |
The following circulators on facets are defined only in dimension 3, though facets are defined also in dimension 2: there are only two facets sharing an edge in dimension 2. | |
| Facet_circulator | incident_facets (Edge e) const |
Starts at an arbitrary facet incident to e. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Edge e, Facet start) const |
Starts at facet start. | |
| Facet_circulator | incident_facets (Edge e, Cell_handle start, int f) const |
Starts at facet of index f in start. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Facet start) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Cell_handle start, int f) const |
As above for edge (i,j) of c and facet (start,f). | |
Traversal of the Incident Cells, Facets and Edges, and the Adjacent Vertices of a Given Vertex | |
| template<class OutputIterator > | |
| OutputIterator | incident_cells (Vertex_handle v, OutputIterator cells) const |
Copies the Cell_handles of all cells incident to v to the output iterator cells. | |
| bool | try_lock_and_get_incident_cells (Vertex_handle v, std::vector< Cell_handle > &cells) const |
Try to lock and copy the Cell_handles of all cells incident to v into cells. | |
| template<class OutputIterator > | |
| OutputIterator | finite_incident_cells (Vertex_handle v, OutputIterator cells) const |
Copies the Cell_handles of all finite cells incident to v to the output iterator cells. | |
| template<class OutputIterator > | |
| OutputIterator | incident_facets (Vertex_handle v, OutputIterator facets) const |
Copies all Facets incident to v to the output iterator facets. | |
| template<class OutputIterator > | |
| OutputIterator | finite_incident_facets (Vertex_handle v, OutputIterator facets) const |
Copies all finite Facets incident to v to the output iterator facets. | |
| template<class OutputIterator > | |
| OutputIterator | incident_edges (Vertex_handle v, OutputIterator edges) const |
Copies all Edges incident to v to the output iterator edges. | |
| template<class OutputIterator > | |
| OutputIterator | finite_incident_edges (Vertex_handle v, OutputIterator edges) const |
Copies all finite Edges incident to v to the output iterator edges. | |
| template<class OutputIterator > | |
| OutputIterator | adjacent_vertices (Vertex_handle v, OutputIterator vertices) const |
Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices. | |
| template<class OutputIterator > | |
| OutputIterator | finite_adjacent_vertices (Vertex_handle v, OutputIterator vertices) const |
Copies the Vertex_handles of all finite vertices adjacent to v to the output iterator vertices. | |
| size_type | degree (Vertex_handle v) const |
| Returns the degree of a vertex, that is, the number of incident vertices. | |
Traversal Between Adjacent Cells | |
| int | mirror_index (Cell_handle c, int i) const |
Returns the index of c in its \( i^{th}\) neighbor. | |
| Vertex_handle | mirror_vertex (Cell_handle c, int i) const |
Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c. | |
| Facet | mirror_facet (Facet f) const |
| Returns the same facet seen from the other adjacent cell. | |
Checking | |
The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of cells and vertices. We provide the user with the following methods to help debugging. | |
| bool | is_valid (bool verbose=false) const |
| This is a function for debugging purpose. | |
| bool | is_valid (Cell_handle c, bool verbose=false) const |
| This is a function for debugging purpose. | |
I/O | |
The information in the When dimension \( <\) 3, the same information is stored for faces of maximal dimension instead of cells. | |
| istream & | operator>> (istream &is, Triangulation_3 &t) |
Reads the underlying combinatorial triangulation from is by calling the corresponding input operator of the triangulation data structure class (note that the infinite vertex is numbered 0), and the non-combinatorial information by calling the corresponding input operators of the vertex and the cell classes (such as point coordinates), which are provided by overloading the stream operators of the vertex and cell types. | |
| ostream & | operator<< (ostream &os, const Triangulation_3 &t) |
Writes the triangulation t into os. | |
| template<typename Tr_src , typename ConvertVertex , typename ConvertCell > | |
| std::istream & | file_input (std::istream &is, ConvertVertex convert_vertex=ConvertVertex(), ConvertCell convert_cell=ConvertCell()) |
The triangulation streamed in is, of original type Tr_src, is written into the triangulation. | |
Concurrency | |
| void | set_lock_data_structure (Lock_data_structure *lock_ds) const |
| Set the pointer to the lock data structure. | |
Additional Inherited Members | |
 Static Public Member Functions inherited from CGAL::Triangulation_utils_3 Static Public Member Functions inherited from CGAL::Triangulation_utils_3 | |
| static unsigned int | next_around_edge (unsigned int i, unsigned int j) |
| static int | vertex_triple_index (const int i, const int j) |
| static unsigned int | ccw (unsigned int i) |
| static unsigned int | cw (unsigned int i) |
| typedef unspecified_type CGAL::Triangulation_3< Traits, TDS, SLDS >::Segment_cell_iterator |
iterator over cells intersected by a line segment.
Segment_cell_iterator implements the concept ForwardIterator and is non-mutable. Its value type is Cell_handle.
| typedef unspecified_type CGAL::Triangulation_3< Traits, TDS, SLDS >::Segment_simplex_iterator |
iterator over simplices intersected by a line segment.
Segment_simplex_iterator implements the concept ForwardIterator and is non-mutable. Its value type is Triangulation_simplex_3.
| enum CGAL::Triangulation_3::Locate_type |
The enum Locate_type is defined by Triangulation_3 to specify which case occurs when locating a point in the triangulation.
| Enumerator | |
|---|---|
| VERTEX | |
| EDGE | |
| FACET | |
| CELL | |
| OUTSIDE_CONVEX_HULL | |
| OUTSIDE_AFFINE_HULL | |
| CGAL::Triangulation_3< Traits, TDS, SLDS >::Triangulation_3 | ( | const Geom_traits & | traits = Geom_traits(), |
| Lock_data_structure * | lock_ds = nullptr |
||
| ) |
Introduces a triangulation t having only one vertex which is the infinite vertex.
lock_ds is an optional pointer to the lock data structure for parallel operations. It must be provided if concurrency is enabled.
| CGAL::Triangulation_3< Traits, TDS, SLDS >::Triangulation_3 | ( | const Triangulation_3< Traits, TDS, SLDS > & | tr | ) |
Copy constructor.
All vertices and faces are duplicated. The pointer to the lock data structure is not copied. Thus, the copy won't be concurrency-safe as long as the user has not call Triangulation_3::set_lock_data_structure.
| OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::adjacent_vertices | ( | Vertex_handle | v, |
| OutputIterator | vertices | ||
| ) | const |
Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices.
If t.dimension() < 0, then do nothing. Returns the resulting output iterator.
v != Vertex_handle(), t.is_vertex(v). | All_cell_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::all_cell_handles | ( | ) | const |
returns a range of iterators over all cells (even the infinite cells).
Returns an empty range when t.number_of_cells() == 0.
All_cells_iterator is Cell, the value type of All_cell_handles::iterator is Cell_handle. | All_cells_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_cells_begin | ( | ) | const |
Starts at an arbitrary cell.
Iterates over all cells (even infinite ones). Returns cells_end() when t.dimension() < 3.
| All_edges CGAL::Triangulation_3< Traits, TDS, SLDS >::all_edges | ( | ) | const |
returns a range of iterators starting at an arbitrary edge.
Returns an empty range when t.dimension() < 2.
| All_edges_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_edges_begin | ( | ) | const |
Starts at an arbitrary edge.
Iterates over all edges (even infinite ones). Returns edges_end() when t.dimension() < 1.
| All_facets CGAL::Triangulation_3< Traits, TDS, SLDS >::all_facets | ( | ) | const |
returns a range of iterators starting at an arbitrary facet.
Returns an empty range when t.dimension() < 2.
| All_facets_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_facets_begin | ( | ) | const |
Starts at an arbitrary facet.
Iterates over all facets (even infinite ones). Returns facets_end() when t.dimension() < 2.
| All_vertex_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::all_vertex_handles | ( | ) | const |
returns a range of iterators over all vertices (even the infinite one).
All_vertices_iterator is Vertex, the value type of All_vertex_handles::iterator is Vertex_handle. | All_vertices_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::all_vertices_begin | ( | ) | const |
Starts at an arbitrary vertex.
Iterates over all vertices (even the infinite one).
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::are_equal | ( | const Facet & | f, |
| Cell_handle | n, | ||
| int | j | ||
| ) | const |
For these three methods:
t.dimension() == 3. | size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::degree | ( | Vertex_handle | v | ) | const |
Returns the degree of a vertex, that is, the number of incident vertices.
The infinite vertex is counted.
v != Vertex_handle(), t.is_vertex(v). | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_adjacent_vertices | ( | Vertex_handle | v, |
| OutputIterator | vertices | ||
| ) | const |
Copies the Vertex_handles of all finite vertices adjacent to v to the output iterator vertices.
If t.dimension() < 0, then do nothing. Returns the resulting output iterator.
v != Vertex_handle(), t.is_vertex(v). | Finite_cell_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_cell_handles | ( | ) | const |
returns a range of iterators over finite cells.
Returns an empty range when t.number_of_cells() == 0.
Finite_cells_iterator is Cell, the value type of Finite_cell_handles::iterator is Cell_handle. | Finite_cells_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_cells_begin | ( | ) | const |
Starts at an arbitrary finite cell.
Then ++ and -- will iterate over finite cells. Returns finite_cells_end() when t.dimension() < 3.
| Finite_edges CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_edges | ( | ) | const |
returns a range of iterators starting at an arbitrary edge.
Returns an empty range when t.dimension() < 2.
| Finite_edges_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_edges_begin | ( | ) | const |
Starts at an arbitrary finite edge.
Then ++ and -- will iterate over finite edges.
| Finite_facets CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_facets | ( | ) | const |
returns a range of iterators starting at an arbitrary facet.
Returns an empty range when t.dimension() < 2.
| Finite_facets_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_facets_begin | ( | ) | const |
Starts at an arbitrary finite facet.
Then ++ and -- will iterate over finite facets. Returns finite_facets_end() when t.dimension() < 2.
| OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_cells | ( | Vertex_handle | v, |
| OutputIterator | cells | ||
| ) | const |
Copies the Cell_handles of all finite cells incident to v to the output iterator cells.
Returns the resulting output iterator.
t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v). | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_edges | ( | Vertex_handle | v, |
| OutputIterator | edges | ||
| ) | const |
Copies all finite Edges incident to v to the output iterator edges.
Returns the resulting output iterator.
t.dimension() > 0, v != Vertex_handle(), t.is_vertex(v). | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_incident_facets | ( | Vertex_handle | v, |
| OutputIterator | facets | ||
| ) | const |
Copies all finite Facets incident to v to the output iterator facets.
Returns the resulting output iterator.
t.dimension() > 1, v != Vertex_handle(), t.is_vertex(v). | Finite_vertex_handles CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_vertex_handles | ( | ) | const |
returns a range of iterators over finite vertices.
Finite_vertices_iterator is Vertex, the value type of Finite_vertex_handles::iterator is Vertex_handle. | Finite_vertices_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::finite_vertices_begin | ( | ) | const |
Starts at an arbitrary finite vertex.
Then ++ and -- will iterate over finite vertices.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::flip | ( | Cell_handle | c, |
| int | i | ||
| ) |
Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive).
They return false or true according to this test.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::flip | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) |
Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive).
They return false or true according to this test.
| void CGAL::Triangulation_3< Traits, TDS, SLDS >::flip_flippable | ( | Cell_handle | c, |
| int | i | ||
| ) |
Should be preferred to the previous methods when the facet is known to be flippable.
| void CGAL::Triangulation_3< Traits, TDS, SLDS >::flip_flippable | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) |
Should be preferred to the previous methods when the edge is known to be flippable.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::has_vertex | ( | Cell_handle | c, |
| int | i, | ||
| Vertex_handle | v, | ||
| int & | j | ||
| ) | const |
Same for facet (c,i).
Computes the index j of v in c.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::has_vertex | ( | const Facet & | f, |
| Vertex_handle | v, | ||
| int & | j | ||
| ) | const |
If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true.
t.dimension() == 3 | Cell_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells | ( | Edge | e | ) | const |
Starts at an arbitrary cell incident to e.
t.dimension() == 3. | Cell_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells | ( | Edge | e, |
| Cell_handle | start | ||
| ) | const |
Starts at cell start.
t.dimension() == 3 and start is incident to e. | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_cells | ( | Vertex_handle | v, |
| OutputIterator | cells | ||
| ) | const |
Copies the Cell_handles of all cells incident to v to the output iterator cells.
Returns the resulting output iterator.
t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v). | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_edges | ( | Vertex_handle | v, |
| OutputIterator | edges | ||
| ) | const |
Copies all Edges incident to v to the output iterator edges.
Returns the resulting output iterator.
t.dimension() > 0, v != Vertex_handle(), t.is_vertex(v). | Facet_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets | ( | Edge | e | ) | const |
Starts at an arbitrary facet incident to e.
t.dimension() == 3 | Facet_circulator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets | ( | Edge | e, |
| Facet | start | ||
| ) | const |
Starts at facet start.
start is incident to e. | OutputIterator CGAL::Triangulation_3< Traits, TDS, SLDS >::incident_facets | ( | Vertex_handle | v, |
| OutputIterator | facets | ||
| ) | const |
Copies all Facets incident to v to the output iterator facets.
Returns the resulting output iterator.
t.dimension() > 1, v != Vertex_handle(), t.is_vertex(v). | Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::inexact_locate | ( | const Point & | query, |
| Cell_handle | start = Cell_handle() |
||
| ) | const |
Same as locate() but uses inexact predicates.
This function returns a handle on a cell that is a good approximation of the exact location of query, while being faster. Note that it may return a handle on a cell whose interior does not contain query. When the triangulation has dimension smaller than 3, start is returned.
Note that this function is available only if the cartesian coordinates of query are accessible with functions x(), y() and z().
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert | ( | const Point & | p, |
| Cell_handle | start = Cell_handle() |
||
| ) |
Inserts the point p in the triangulation and returns the corresponding vertex.
If point p coincides with an already existing vertex, this vertex is returned and the triangulation remains unchanged.
If point p lies in the convex hull of the points, it is added naturally: if it lies inside a cell, the cell is split into four cells, if it lies on a facet, the two incident cells are split into three cells, if it lies on an edge, all the cells incident to this edge are split into two cells.
If point p is strictly outside the convex hull but in the affine hull, p is linked to all visible points on the convex hull to form the new triangulation. See Figure Triangulation3figinsert_outside_convex_hull.
If point p is outside the affine hull of the points, p is linked to all the points, and the dimension of the triangulation is incremented. All the points now belong to the boundary of the convex hull, so, the infinite vertex is linked to all the points to triangulate the new infinite face. See Figure Triangulation3figinsert_outside_affine_hull. The optional argument start is used as a starting place for the search.
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert | ( | const Point & | p, |
| Locate_type | lt, | ||
| Cell_handle | loc, | ||
| int | li, | ||
| int | lj | ||
| ) |
| std::ptrdiff_t CGAL::Triangulation_3< Traits, TDS, SLDS >::insert | ( | PointWithInfoInputIterator | first, |
| PointWithInfoInputIterator | last | ||
| ) |
Inserts the points in the iterator range [first,last) in the given order, and returns the number of inserted points.
Given a pair (p,i), the vertex v storing p also stores i, that is v.point() == p and v.info() == i. If several pairs have the same point, only one vertex is created, and one of the objects of type Vertex::Info will be stored in the vertex.
Vertex must be model of the concept TriangulationVertexBaseWithInfo_3.| PointWithInfoInputIterator | must be an input iterator with the value type std::pair<Point,Vertex::Info>. |
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_cell | ( | const Point & | p, |
| Cell_handle | c | ||
| ) |
Inserts the point p in the cell c.
The cell c is split into 4 tetrahedra.
t.dimension() == 3 and p lies strictly inside cell c. | Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_edge | ( | const Point & | p, |
| Cell_handle | c, | ||
| int | i, | ||
| int | j | ||
| ) |
As above, inserts p in the edge \( (i, j)\) of c.
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_edge | ( | const Point & | p, |
| const Edge & | e | ||
| ) |
Inserts p in the edge e.
In dimension 3, all the cells having this edge are split into 2 tetrahedra; in dimension 2, the 2 neighboring facets are split into 2 triangles; in dimension 1, the edge is split into 2 edges.
t.dimension() \( \geq1\) and p lies on edge e. | Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_facet | ( | const Point & | p, |
| Cell_handle | c, | ||
| int | i | ||
| ) |
As above, insertion in the facet (c,i).
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_facet | ( | const Point & | p, |
| const Facet & | f | ||
| ) |
Inserts the point p in the facet f.
In dimension 3, the 2 neighboring cells are split into 3 tetrahedra; in dimension 2, the facet is split into 3 triangles.
t.dimension() \( \geq2\) and p lies strictly inside face f. | Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_in_hole | ( | const Point & | p, |
| CellIt | cell_begin, | ||
| CellIt | cell_end, | ||
| Cell_handle | begin, | ||
| int | i | ||
| ) |
Creates a new vertex by starring a hole.
It takes an iterator range [cell_begin,cell_end) of Cell_handles which specifies a hole: a set of connected cells (resp. facets in dimension 2) which is star-shaped wrt p. (begin, i) is a facet (resp. an edge) on the boundary of the hole, that is, begin belongs to the set of cells (resp. facets) previously described, and begin->neighbor(i) does not. Then this function deletes all the cells (resp. facets) describing the hole, creates a new vertex v, and for each facet (resp. edge) on the boundary of the hole, creates a new cell (resp. facet) with v as vertex. Then v->set_point(p) is called and v is returned.
This operation is equivalent to calling tds().insert_in_hole(cell_begin, cell_end, begin, i); v->set_point(p).
t.dimension() \( \geq2\), the set of cells (resp. facets in dimension 2) is connected, its boundary is connected, and p lies inside the hole, which is star-shaped wrt p. | Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_outside_affine_hull | ( | const Point & | p | ) |
p is linked to all the points, and the infinite vertex is linked to all the points (including p) to triangulate the new infinite face, so that all the points now belong to the boundary of the convex hull.
See Figure Triangulation3figinsert_outside_affine_hull.
This method can be used to insert the first point in an empty triangulation.
t.dimension() < 3 and p lies outside the affine hull of the points.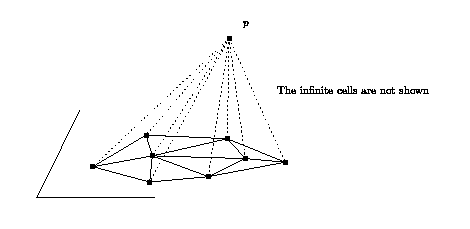
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::insert_outside_convex_hull | ( | const Point & | p, |
| Cell_handle | c | ||
| ) |
The cell c must be an infinite cell containing p.
Links p to all points in the triangulation that are visible from p. Updates consequently the infinite faces. See Figure Triangulation3figinsert_outside_convex_hull.
t.dimension() > 0, c, and the \( k\)-face represented by c is infinite and contains t.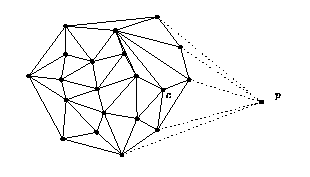
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_cell | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Vertex_handle | w, | ||
| Vertex_handle | x, | ||
| Cell_handle & | c | ||
| ) | const |
Tests whether (u,v,w,x) is a cell of t and computes this cell c.
u, v, w and x are vertices of t. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_cell | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Vertex_handle | w, | ||
| Vertex_handle | x, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j, | ||
| int & | k, | ||
| int & | l | ||
| ) | const |
Tests whether (u,v,w,x) is a cell of t.
If the cell c is found, the method computes the indices i, j, k and l of the vertices u, v, w and x in c, in this order.
u, v, w and x are vertices of t. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_edge | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j | ||
| ) | const |
Tests whether (u,v) is an edge of t.
If the edge is found, it gives a cell c having this edge and the indices i and j of the vertices u and v in c, in this order.
u and v are vertices of t. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_facet | ( | Vertex_handle | u, |
| Vertex_handle | v, | ||
| Vertex_handle | w, | ||
| Cell_handle & | c, | ||
| int & | i, | ||
| int & | j, | ||
| int & | k | ||
| ) | const |
Tests whether (u,v,w) is a facet of t.
If the facet is found, it computes a cell c having this facet and the indices i, j and k of the vertices u, v and w in c, in this order.
u, v and w are vertices of t. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite | ( | Cell_handle | c | ) | const |
true, iff c is incident to the infinite vertex.
t.dimension() == 3. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
true, iff the facet i of cell c is incident to the infinite vertex.
t.dimension() \( \geq2\) and \( i\in\{0,1,2,3\}\) in dimension 3, \( i=3\) in dimension 2. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) | const |
true, iff the edge (i,j) of cell c is incident to the infinite vertex.
t.dimension() \( \geq1\) and \( i\neq j\). Moreover \( i,j \in\{0,1,2,3\}\) in dimension 3, \( i,j \in\{0,1,2\}\) in dimension 2, \( i,j \in\{0,1\}\) in dimension 1. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite | ( | const Edge & | e | ) | const |
true iff edge e is incident to the infinite vertex.
t.dimension() \( \geq1\). | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_infinite | ( | const Facet & | f | ) | const |
true iff facet f is incident to the infinite vertex.
t.dimension() \( \geq2\). | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_valid | ( | bool | verbose = false | ) | const |
This is a function for debugging purpose.
Checks the combinatorial validity of the triangulation. Checks also the validity of its geometric embedding (see Section Representation). When verbose is set to true, messages describing the first invalidity encountered are printed.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_valid | ( | Cell_handle | c, |
| bool | verbose = false |
||
| ) | const |
This is a function for debugging purpose.
Checks the combinatorial validity of the cell by calling the is_valid method of the cell class. Also checks the geometric validity of c, if c is finite. (See Section Representation.)
When verbose is set to true, messages are printed to give a precise indication of the kind of invalidity encountered.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::is_vertex | ( | const Point & | p, |
| Vertex_handle & | v | ||
| ) | const |
Tests whether p is a vertex of t by locating p in the triangulation.
If p is found, the associated vertex v is given.
| Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::locate | ( | const Point & | query, |
| Cell_handle | start = Cell_handle(), |
||
| bool * | could_lock_zone = nullptr |
||
| ) | const |
If the point query lies inside the convex hull of the points, the cell that contains the query in its interior is returned.
If query lies on a facet, an edge or on a vertex, one of the cells having query on its boundary is returned.
If the point query lies outside the convex hull of the points, an infinite cell with vertices \( \{ p, q, r, \infty\}\) is returned such that the tetrahedron \( ( p, q, r, query )\) is positively oriented (the rest of the triangulation lies on the other side of facet \( ( p, q, r )\)).
Note that locate works even in degenerate dimensions: in dimension 2 (resp. 1, 0) the Cell_handle returned is the one that represents the facet (resp. edge, vertex) containing the query point.
The optional argument start is used as a starting place for the search.
The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. When the pointer is not null, the locate will try to lock all the cells along the walk. If it succeeds, *could_lock_zone is true, otherwise it is false. In any case, the locked cells are not unlocked by locate, leaving this choice to the user.
| Cell_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::locate | ( | const Point & | query, |
| Locate_type & | lt, | ||
| int & | li, | ||
| int & | lj, | ||
| Cell_handle | start = Cell_handle(), |
||
| bool * | could_lock_zone = nullptr |
||
| ) | const |
If query lies inside the affine hull of the points, the \( k\)-face (finite or infinite) that contains query in its interior is returned, by means of the cell returned together with lt, which is set to the locate type of the query (VERTEX, EDGE, FACET, CELL, or OUTSIDE_CONVEX_HULL if the cell is infinite and query lies strictly in it) and two indices li and lj that specify the \( k\)-face of the cell containing query.
If the \( k\)-face is a cell, li and lj have no meaning; if it is a facet (resp. vertex), li gives the index of the facet (resp. vertex) and lj has no meaning; if it is and edge, li and lj give the indices of its vertices.
If the point query lies outside the affine hull of the points, which can happen in case of degenerate dimensions, lt is set to OUTSIDE_AFFINE_HULL, and the cell returned has no meaning. As a particular case, if there is no finite vertex yet in the triangulation, lt is set to OUTSIDE_AFFINE_HULL and locate returns the default constructed handle.
The optional argument start is used as a starting place for the search.
The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. When the pointer is not null, the locate will try to lock all the cells along the walk. If it succeeds, *could_lock_zone is true, otherwise it is false. In any case, the locked cells are not unlocked by locate, leaving this choice to the user.
| int CGAL::Triangulation_3< Traits, TDS, SLDS >::mirror_index | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the index of c in its \( i^{th}\) neighbor.
| Vertex_handle CGAL::Triangulation_3< Traits, TDS, SLDS >::mirror_vertex | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c.
| size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_edges | ( | ) | const |
The number of edges.
Returns 0 if t.dimension() < 1.
| size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_facets | ( | ) | const |
The number of facets.
Returns 0 if t.dimension() < 2.
| size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_cells | ( | ) | const |
The number of finite cells.
Returns 0 if t.dimension() < 3.
| size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_edges | ( | ) | const |
The number of finite edges.
Returns 0 if t.dimension() < 1.
| size_type CGAL::Triangulation_3< Traits, TDS, SLDS >::number_of_finite_facets | ( | ) | const |
The number of finite facets.
Returns 0 if t.dimension() < 2.
| Triangulation_3 & CGAL::Triangulation_3< Traits, TDS, SLDS >::operator= | ( | const Triangulation_3< Traits, TDS, SLDS > & | tr | ) |
The triangulation tr is duplicated, and modifying the copy after the duplication does not modify the original.
The previous triangulation held by t is deleted.
| bool CGAL::Triangulation_3< Traits, TDS, SLDS >::operator== | ( | const Triangulation_3< GT, Tds1 > & | t1, |
| const Triangulation_3< GT, Tds2 > & | t2 | ||
| ) |
Equality operator.
Returns true iff there exist a bijection between the vertices of t1 and those of t2 and a bijection between the cells of t1 and those of t2, which preserve the geometry of the triangulation, that is, the points of each corresponding pair of vertices are equal, and the tetrahedra corresponding to each pair of cells are equal (up to a permutation of their vertices).
| const Point & CGAL::Triangulation_3< Traits, TDS, SLDS >::point | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the point given by vertex i of cell c.
t.dimension() \( \geq0\) and \( i \in\{0,1,2,3\}\) in dimension 3, \( i \in\{0,1,2\}\) in dimension 2, \( i \in\{0,1\}\) in dimension 1, \( i = 0\) in dimension 0, and the vertex is finite. | const Point & CGAL::Triangulation_3< Traits, TDS, SLDS >::point | ( | Vertex_handle | v | ) | const |
Same as the previous method for vertex v.
t.dimension() \( \geq0\) and the vertex is finite. | Segment CGAL::Triangulation_3< Traits, TDS, SLDS >::segment | ( | Cell_handle | c, |
| int | i, | ||
| int | j | ||
| ) | const |
Same as the previous method for edge (c,i,j).
| Segment CGAL::Triangulation_3< Traits, TDS, SLDS >::segment | ( | const Edge & | e | ) | const |
Returns the line segment formed by the vertices of e.
t.dimension() \( \geq1\) and e is finite. | Segment_cell_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_cells_begin | ( | const Point & | ps, |
| const Point & | pt, | ||
| Cell_handle | hint = Cell_handle() |
||
| ) | const |
returns the iterator that allows to visit the cells intersected by the line segment [ps, pt].
If [ps,pt] entirely lies outside the convex hull, the iterator visits exactly one infinite cell.
The initial value of the iterator is the cell containing ps. If more than one cell contains ps (e.g. if ps lies on a vertex), the initial value is the cell intersected by the interior of the line segment [ps,pt]. If ps lies outside the convex hull and pt inside the convex full, the initial value is the infinite cell which finite facet is intersected by the interior of [ps,pt].
The first cell containing pt is the last valid value of the iterator. It is followed by segment_traverser_cells_end().
The optional argument hint can reduce the time to construct the iterator if it is geometrically close to ps.
ps and pt must be different points. triangulation.dimension() >= 2. If the dimension is 2, both ps and pt must lie in the affine hull. | Segment_cell_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_cells_begin | ( | Vertex_handle | vs, |
| Vertex_handle | vt | ||
| ) | const |
returns the iterator that allows to visit the cells intersected by the line segment [vs,vt].
The initial value of the iterator is the cell containing vs and intersected by the line segment [vs,vt] in its interior.
The first cell incident to vt is the last valid value of the iterator. It is followed by segment_traverser_cells_end().
vs and vt must be different vertices and neither can be the infinite vertex. triangulation.dimension() >= 2 | Segment_cell_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_cells_end | ( | ) | const |
returns the past-the-end iterator over the intersected cells.
This iterator cannot be dereferenced. It indicates when the Segment_cell_iterator has passed the target.
triangulation.dimension() >= 2 | Segment_simplex_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_simplices_begin | ( | const Point & | ps, |
| const Point & | pt, | ||
| Cell_handle | hint = Cell_handle() |
||
| ) | const |
returns the iterator that allows to visit the simplices intersected by the line segment [ps,pt].
If [ps,pt] entirely lies outside the convex hull, the iterator visits exactly one infinite cell.
The initial value of the iterator is the lowest dimension simplex containing ps.
The iterator remains valid until the first simplex containing pt is passed.
The optional argument hint can reduce the time to construct the iterator if it is close to ps.
ps and pt must be different points. triangulation.dimension() >= 2. If the dimension is 2, both ps and pt must lie in the affine hull. | Segment_simplex_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_simplices_begin | ( | Vertex_handle | vs, |
| Vertex_handle | vt | ||
| ) | const |
returns the iterator that allows to visit the simplices intersected by the line segment [vs,vt].
The initial value of the iterator is vs. The iterator remains valid until vt is passed.
vs and vt must be different vertices and neither can be the infinite vertex. triangulation.dimension() >= 2 | Segment_simplex_iterator CGAL::Triangulation_3< Traits, TDS, SLDS >::segment_traverser_simplices_end | ( | ) | const |
returns the past-the-end iterator over the intersected simplices.
This iterator cannot be dereferenced. It indicates when the Segment_simplex_iterator has passed the target.
triangulation.dimension() >= 2 | void CGAL::Triangulation_3< Traits, TDS, SLDS >::set_infinite_vertex | ( | Vertex_handle | v | ) |
This is an advanced function.
This method is meant to be used only if you have done a low-level operation on the underlying tds that invalidated the infinite vertex. Sets the infinite vertex.
| Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_cell | ( | const Point & | p, |
| Cell_handle | c, | ||
| Locate_type & | lt, | ||
| int & | li, | ||
| int & | lj | ||
| ) | const |
Returns a value indicating on which side of the oriented boundary of c the point p lies.
More precisely, it returns:
ON_BOUNDED_SIDE if p is inside the cell. For an infinite cell this means that p lies strictly in the half space limited by its finite facet and not containing any other point of the triangulation.ON_BOUNDARY if p on the boundary of the cell. For an infinite cell this means that p lies on the finite facet. Then lt together with li and lj give the precise location on the boundary. (See the descriptions of the locate methods.)ON_UNBOUNDED_SIDE if p lies outside the cell. For an infinite cell this means that p does not satisfy either of the two previous conditions. t.dimension() == 3 | Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_edge | ( | const Point & | p, |
| const Edge & | e, | ||
| Locate_type & | lt, | ||
| int & | li | ||
| ) | const |
Returns a value indicating on which side of the oriented boundary of e the point p lies:
ON_BOUNDED_SIDE if p is inside the edge. For an infinite edge this means that p lies in the half line defined by the vertex and not containing any other point of the triangulation.ON_BOUNDARY if p equals one of the vertices, li give the index of the vertex in the cell storing eON_UNBOUNDED_SIDE if p lies outside the edge. For an infinite edge this means that p lies on the other half line, which contains the other points of the triangulation. t.dimension() == 1 and p is collinear with the points of the triangulation. e.second == 0 and e.third \( =1\) (in dimension 1 there is only one edge per cell). | Bounded_side CGAL::Triangulation_3< Traits, TDS, SLDS >::side_of_facet | ( | const Point & | p, |
| const Facet & | f, | ||
| Locate_type & | lt, | ||
| int & | li, | ||
| int & | lj | ||
| ) | const |
Returns a value indicating on which side of the oriented boundary of f the point p lies:
ON_BOUNDED_SIDE if p is inside the facet. For an infinite facet this means that p lies strictly in the half plane limited by its finite edge and not containing any other point of the triangulation .ON_BOUNDARY if p is on the boundary of the facet. For an infinite facet this means that p lies on the finite edge. lt, li and lj give the precise location of p on the boundary of the facet. li and lj refer to indices in the degenerate cell c representing f.ON_UNBOUNDED_SIDE if p lies outside the facet. For an infinite facet this means that p does not satisfy either of the two previous conditions.t.dimension() == 2 and p lies in the plane containing the triangulation. f.second \( =3\) (in dimension 2 there is only one facet per cell). | void CGAL::Triangulation_3< Traits, TDS, SLDS >::swap | ( | Triangulation_3< Traits, TDS, SLDS > & | tr | ) |
The triangulations tr and t are swapped.
t.swap(tr) should be preferred to t = tr or to t(tr) if tr is deleted after that. Indeed, there is no copy of cells and vertices, thus this method runs in constant time.
| Triangulation_data_structure & CGAL::Triangulation_3< Traits, TDS, SLDS >::tds | ( | ) |
Returns a reference to the triangulation data structure.
This method is mainly a help for users implementing their own triangulation algorithms. The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of the tds.
| Tetrahedron CGAL::Triangulation_3< Traits, TDS, SLDS >::tetrahedron | ( | Cell_handle | c | ) | const |
Returns the tetrahedron formed by the four vertices of c.
t.dimension() == 3 and the cell is finite. | Triangle CGAL::Triangulation_3< Traits, TDS, SLDS >::triangle | ( | Cell_handle | c, |
| int | i | ||
| ) | const |
Returns the triangle formed by the three vertices of facet (c,i).
The triangle is oriented so that its normal points to the inside of cell c.
t.dimension() \( \geq2\) and \( i \in\{0,1,2,3\}\) in dimension 3, \( i = 3\) in dimension 2, and the facet is finite. | Triangle CGAL::Triangulation_3< Traits, TDS, SLDS >::triangle | ( | const Facet & | f | ) | const |
Same as the previous method for facet f.
t.dimension() \( \geq2\) and the facet is finite. | bool CGAL::Triangulation_3< Traits, TDS, SLDS >::try_lock_and_get_incident_cells | ( | Vertex_handle | v, |
| std::vector< Cell_handle > & | cells | ||
| ) | const |
Try to lock and copy the Cell_handles of all cells incident to v into cells.
Returns true in case of success. Otherwise, cells is emptied and the function returns false. In any case, the locked cells are not unlocked by try_lock_and_get_incident_cells(), leaving this choice to the user.
t.dimension() == 3, v != Vertex_handle(), t.is_vertex(v).