Chapter 12
2D Regularized Boolean Set-Operations

Efi Fogel, Ron Wein, Baruch Zukerman, and Dan Halperin

12.1   Introduction

Figure:  Examples of Boolean set-operations on general polygons.

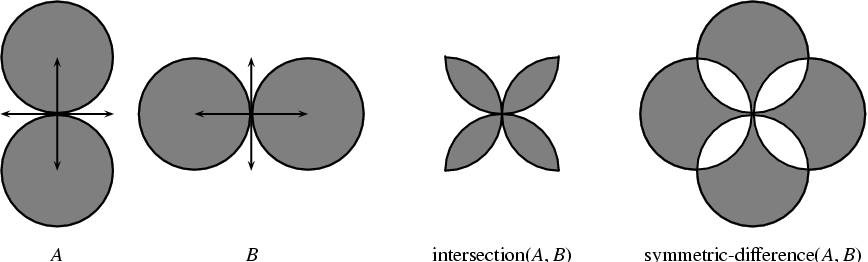
This package consists of the implementation of Boolean set-operations on point sets bounded by $$x-monotone curves¹ in 2-dimensional Euclidean space. In particular, it contains the implementation of regularized Boolean set-operations, intersection predicates, and point containment predicates. Figure 12.1 shows simple examples of such operations.

A regularized Boolean set-operation $$op$$^* can be obtained by first taking the interior of the resultant point set of an ordinary Boolean set-operation $$(P op$$ Q) and then by taking the closure [Hof04]. That is, $$P op$$^* Q = closure$$(interior$$ (P op$$ Q)). Regularized Boolean set-operations appear in Constructive Solid Geometry (CSG), because regular sets are closed under regularized Boolean set-operations, and because regularization eliminates lower dimensional features, namely isolated vertices and antennas, thus simplifying and restricting the representation to physically meaningful solids. Our package provides regularized operations on polygons and general polygons, where the edges of a general polygon may be general $$x-monotone curves, rather than being simple line segments. Ordinary Boolean set-operations, which distinguish between the interior and the boundary of a polygon, are not implemented within this package. The Nef_2 package supports these operations for (linear) polygons; see Chapter 13.

In the rest of this chapter we use - unless otherwise stated - the traditional notation to designate regularized operations; e.g., $$P Q means the regularized intersection of $$P and $$Q.

A polygon $$P is said to be simple (or Jordan) if the only points of the plane belonging to two polygon edges of $$P are the polygon vertices of $$P. Namely, the polygon edges are pairwise disjoint in their interior. Such a polygon has a well-defined interior and exterior and is topologically equivalent to a disk. A polygon in our context must be simple and its vertices must be ordered in a counterclockwise direction around the interior of the polygon.

²

Our package supports the following Boolean set-operations on two point sets $$P and $$Q that are comprised of general polygons:

Intersection

computes the intersection $$R = P Q.

Join

computes the union $$R = P Q.

Difference

computes the difference $$R = P Q.

Symmetric Difference

computes the symmetric difference $$P = P Q = (P Q) (Q P).

Complement

computes the complement R = P.

Intersection predicate

tests whether the two sets $$P and $$Q overlap, distinguishing three possible scenarios: (i) the two sets intersect on their interior (that is, their regularized intersection is not empty $$P Q ); (ii) the boundaries of two sets intersect but their interiors are disjoint; namely they have a finite number of common points or even share a boundary curve (still in this case $$P Q = ; and (iii) the two sets are disjoint.

In the rest of this chapter we review the Boolean set-operations package in more depth. In Section 12.2 we focus on Boolean set-operations on linear polygons, introducing the notion of polygons with holes and of a general polygon set. Section 12.3 introduces general polygons. We first discuss polygons whose edges are either line segements or circular arcs and then explain how to construct and use general polygons whose edges can be arbitrary $$x-monotone curves.

12.2   Boolean Set-Operations on Linear Polygons

The basic library of CGAL includes the Polygon_2<Kernel,Container> class-template that represents a linear polygon in the plane. The polygon is represented by its vertices stored in a container of objects of type Kernel::Point_2. The polygon edges are line segments (Kenrel::Segment_2 objects) between adjacent points in the container. By default, the Container is a vector of Kernel::Point_2 objects.

The following function demonstrates how to use the basic access functions of the Polygon_2 class. It accepts a polygon $$P and prints it in a readable format:

template<class Kernel, class Container>
void print_polygon (const CGAL::Polygon_2<Kernel, Container>& P)
{
  typename CGAL::Polygon_2<Kernel, Container>::Vertex_const_iterator  vit;

  std::cout << "[ " << P.size() << " vertices:";
  for (vit = P.vertices_begin(); vit != P.vertices_end(); ++vit)
    std::cout << " (" << *vit << ')';
  std::cout << " ]" << std::endl;
}

In this section we use the term polygon to indicate a Polygon_2 instance, namely, a polygon having linear edges. General polygons are only discussed in Section 12.3.

The basic components of our package are the free (global) functions complement() that accepts a single Polygon_2 object, and intersection(), join(),², difference(), symmetric_difference() and the predicate do_intersect() that accept two Polygon_2 objects as their input. We explain how these functions should be used throught several examples in the following sections.

A Simple Example

//! \file examples/Boolean_set_operations_2/ex_do_intersect.C
// Determining whether two triangles intersect.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Boolean_set_operations_2.h>

typedef CGAL::Cartesian<Number_type>                    Kernel;
typedef Kernel::Point_2                                 Point_2;
typedef CGAL::Polygon_2<Kernel>                         Polygon_2;

#include "print_utils.h"

int main ()
{
  Polygon_2 P;
  P.push_back (Point_2 (-1,1));
  P.push_back (Point_2 (0,-1));
  P.push_back (Point_2 (1,1));
  std::cout << "P = "; print_polygon (P);

  Polygon_2 Q;
  Q.push_back(Point_2 (-1,-1));
  Q.push_back(Point_2 (1,-1));
  Q.push_back(Point_2 (0,1));
  std::cout << "Q = "; print_polygon (Q);
  
  if ((CGAL::do_intersect (P, Q)))
    std::cout << "The two polygons intersect in their interior." << std::endl;
  else
    std::cout << "The two polygons do not intersect." << std::endl;

  return 0;
}

12.2.1   Polygons with Holes

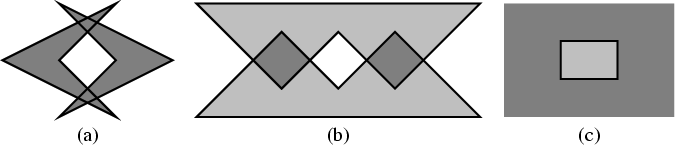
In many cases a binary operation that operates on two strictly simple polygons that have no holes may result in a set of polygon that contains holes in their interior (see Figure 12.2.1 (a)), or a set of disjoint polygons (see Figure 12.2.1 (b); a similar set may result from the union, or the symmetric difference, of two disjoint polygons). Moreover, the complement of a simple polygon is an unbounded set that contains a hole; see Figure 12.2.1 (c).

Regular sets are closed under regularized Boolean set-operations. These operations accept as input, and may result as output, polygons with holes. A polygon with holes represents a point set that may be bounded or unbounded. In case of a bounded set, its outer boundary is represented as a simple (but not necessarily strictly simple) polygon, whose vertices are oriented in a counterclockwise order around the interior of the set. In addition, the set may contain holes, where each hole is represented as a strictly simple polygon, whose vertices are oriented in a clockwise order around the interior of the hole. Note that an unbounded polygon without holes spans the entire plane. Vertices of holes may coincide with vertices of the boundary; see below for an example.

A point set represented by a polygon with holes is considered to be closed. Therefore, the boundaries of the holes are parts of the set (and not part of the holes). The exact definition of the obtained polygon with holes as a result of a Boolean set-operation or a sequence of such operations is closely related to the definition of regularized Boolean set-operations, being the closure of the interior of the corresponding ordinary operation as explained next.

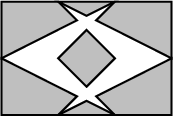
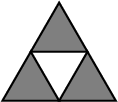Consider, for example, the regular set depicted on the right, which is the result of the union of three small triangles translated appropriately. Alternatively, the same set can be reached by taking the difference between a large triangle and a small upside-down triangle. In general, there are many ways to arrive at a particular point set. However, the set of polygons with holes obtained through the application of any sequence of operations is unique. The set depicted on the right is represented as a single polygon having a triangular outer boundary with a single triangluar hole in its interior - and not as three triangles that have no holes at all. As a general rule, if two point sets are connected, then they belong to the same polygon with holes.

The class template Polygon_with_holes_2<Kernel,Container> represents polygons with holes as described above, where the outer boundary and the hole boundaries are realized as Polygon_2<Kernel,Container> objects. Given an instance $$P of the Polygon_with_holes_2 class, you can use the predicate is_unbounded() to check whether $$P is a unbounded set. If it is bounded, you can obtain the counterclockwise-oriented polygon that represents its outer boundary through the member function outer_boundary(). You can also traverse the holes of $$P through holes_begin() and holes_end(). The two functions return iterators of the nested type Polygon_with_holes_2::Hole_const_iterator that defines the valid range of $$P's holes. The value type of this iterator is Polygon_2.

The following function demonstrates how to traverse a polygon with holes. It accepts a Polygon_with_holes_2 object and uses the auxiliary function print_polygon() to prints all its components in a readable format:

template<class Kernel, class Container>
void print_polygon_with_holes(const CGAL::Polygon_with_holes_2<Kernel, Container> & pwh)
{
  if (! pwh.is_unbounded()) {
    std::cout << "{ Outer boundary = "; 
    print_polygon (pwh.outer_boundary());
  }
  else
    std::cout << "{ Unbounded polygon." << std::endl;

  typename CGAL::Polygon_with_holes_2<Kernel,Container>::Holes_const_iterator hit;
  unsigned int k = 1;

  std::cout << "  " << pwh.number_of_holes() << " holes:" << std::endl;
  for (hit = pwh.holes_begin(); hit != pwh.holes_end(); ++hit, ++k) {
    std::cout << "    Hole #" << k << " = ";
    print_polygon (*hit);
  }
  std::cout << " }" << std::endl;
}

The simple versions of the free functions mentioned therefore accept two Polygon_2 object $$P and $$Q as their input, while their output is given using polygon with holes instances:

• The complement of a simple polygon $$P is always an unbounded set with a single polygonal hole. The function complement(P) therefore returns a polygon-with-holes object that represents the complement of $$P.
• The union of two polygons $$P and $$Q is always a single connected set, unless of course the two input polygons are completely disjoint. In the latter case $$P Q trivially consists of the two input polygons. The free function join(P, Q, R) therefore returns a Boolean value indicating whether $$P Q . If the two polygons are not disjoint, it assignes the a polygon with holes object $$R (which it accepts by reference) with the union of the regularized union operation $$P Q.
• The other three functions, namely intersection(P, Q, oi), difference(P, Q, oi) and symmetric_difference(P, Q, oi), all have a similar interface. As the result of these operation may consist of several disconnected components, they all accept an output iterator oi, whose value type is Polygon_with_holes_2, and add the output polygons to its associated container.

Example - Joining and Intersecting Simple Polygons

The following example demonstartes the usage of the free functions join() and intersect() for computing the union and the intersection of the two simple polygons depicted in Figure 12.2.1 (b). The example uses the auxiliary function print_polygon_with_holes() listed above, which is located in the header file print_utils.h under the examples folder.

//! \file examples/Boolean_set_operations_2/ex_simple_join_intersect.C
// Computing the union and the intersection of two simple polygons.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Boolean_set_operations_2.h>
#include <list>

typedef CGAL::Cartesian<Number_type>               Kernel;
typedef Kernel::Point_2                            Point_2;
typedef CGAL::Polygon_2<Kernel>                    Polygon_2;
typedef CGAL::Polygon_with_holes_2<Kernel>         Polygon_with_holes_2;
typedef std::list<Polygon_with_holes_2>            Pwh_list_2;

#include "print_utils.h"

int main ()
{
  // Construct the two input polygons.
  Polygon_2 P;
  P.push_back (Point_2 (0, 0));
  P.push_back (Point_2 (5, 0));
  P.push_back (Point_2 (3.5, 1.5));
  P.push_back (Point_2 (2.5, 0.5));
  P.push_back (Point_2 (1.5, 1.5));
     
  std::cout << "P = "; print_polygon (P);

  Polygon_2 Q;
  Q.push_back (Point_2 (0, 2));
  Q.push_back (Point_2 (1.5, 0.5));
  Q.push_back (Point_2 (2.5, 1.5));
  Q.push_back (Point_2 (3.5, 0.5));
  Q.push_back (Point_2 (5, 2));
     
  std::cout << "Q = "; print_polygon (Q);

  // Compute the union of P and Q.
  Polygon_with_holes_2 unionR;

  if (CGAL::join (P, Q, unionR)) {
    std::cout << "The union: ";
    print_polygon_with_holes (unionR);
  } else
    std::cout << "P and Q are disjoint and their union is trivial." 
              << std::endl;
  std::cout << std::endl;

  // Compute the intersection of P and Q.
  Pwh_list_2                  intR;
  Pwh_list_2::const_iterator  it;

  CGAL::intersection (P, Q, std::back_inserter(intR));

  std::cout << "The intersection:" << std::endl;
  for (it = intR.begin(); it != intR.end(); ++it) {
    std::cout << "--> ";
    print_polygon_with_holes (*it);
  }
  
  return 0;
}

Operations on Polygons with Holes

Having introduced polygons with holes and explained how the free functions output such objects, it is only natural to perform operations on sets that are represented as polygon with holes, rather than simple polygons. Indeed, the Boolean set-operations package provides overriden free functions complement(), intersection(), join(), difference(), symmetric_difference() and do_intersect() that accept General_polygon_with_holes_2 objects as their input. The prototypes of most functions is the same as of their simpler counterparts that operate on simple polygons. The only exception is complement(P, oi), which outputs a range of polygons with holes that represents the complement of the polygon with holes $$P.

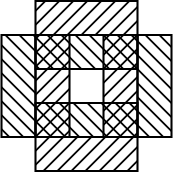The following example demonstrates how to compute the symmetric difference between two sets that contain holes. Each set is a rectangle that contains a rectangular hole in its interior, such that the symmetric difference between the two sets is a single polygon that contains of five holes:

//! \file examples/Boolean_set_operations_2/ex_symmetric_difference.C
// Computing the symmetric difference of two polygons with holes.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Boolean_set_operations_2.h>
#include <list>

typedef CGAL::Cartesian<Number_type>               Kernel;
typedef Kernel::Point_2                            Point_2;
typedef CGAL::Polygon_2<Kernel>                    Polygon_2;
typedef CGAL::Polygon_with_holes_2<Kernel>         Polygon_with_holes_2;
typedef std::list<Polygon_with_holes_2>            Pwh_list_2;

#include "print_utils.h"

int main ()
{
  // Construct P - a bounded rectangle that contains a rectangular hole.
  Polygon_2 outP;
  Polygon_2 holesP[1];

  outP.push_back (Point_2 (-3, -5));  outP.push_back (Point_2 (3, -5));
  outP.push_back (Point_2 (3, 5));    outP.push_back (Point_2 (-3, 5));
  holesP[0].push_back (Point_2 (-1, -3));
  holesP[0].push_back (Point_2 (-1, 3));
  holesP[0].push_back (Point_2 (1, 3));
  holesP[0].push_back (Point_2 (1, -3));

  Polygon_with_holes_2  P (outP, holesP, holesP + 1); 
  std::cout << "P = "; print_polygon_with_holes (P);

  // Construct Q - a bounded rectangle that contains a rectangular hole.
  Polygon_2 outQ;
  Polygon_2 holesQ[1];

  outQ.push_back (Point_2 (-5, -3));  outQ.push_back (Point_2 (5, -3));
  outQ.push_back (Point_2 (5, 3));    outQ.push_back (Point_2 (-5, 3));
  holesQ[0].push_back (Point_2 (-3, -1));
  holesQ[0].push_back (Point_2 (-3, 1));
  holesQ[0].push_back (Point_2 (3, 1));
  holesQ[0].push_back (Point_2 (3, -1));

  Polygon_with_holes_2  Q (outQ, holesQ, holesQ + 1);
  std::cout << "Q = "; print_polygon_with_holes (Q);

  // Compute the symmetric difference of P and Q.
  Pwh_list_2 symmR;
  Pwh_list_2::const_iterator it;

  CGAL::symmetric_difference (P, Q, std::back_inserter(symmR));

  std::cout << "The symmetric difference:" << std::endl;
  for (it = symmR.begin(); it != symmR.end(); ++it) {
    std::cout << "--> "; 
    print_polygon_with_holes (*it);
  }

  return 0;
}

12.2.2   Operating on Polygon Sets

We argue that the result of a regularized operations on two polygons (or polygons with holes) $$P and $$Q is typically a collection of several disconnected polygons with holes. It is only natural to represent such a collection in terms of a class, making it possible to operate on the set resulting from computing, for example, $$P Q.

A central component in the Boolean set-operations package is the Polygon_set_2<Kernel, Container> class-template. An instance of this class represents a point set formed by the collection of several disconnected polygons with holes. It employs the Arrangement_2 class to represent this point set in the plane as a planar arrangement; see Chapter 17.

An instance $$S of a Polygon_set_2 class usually represents the result of a sequence of operations that were applied on some input polygons. The representation of $$S is unique, regardless of the particular sequence of operations that were applied in order to arrive at it.

In addition, a polygon-set object can be constructed from a single polygon object or from a polygon-with-holes object. Once constructed, it is possible to insert new polygons (or polygons with holes) into the set using the insert() method, as long as the inserted polygons and the existing polygons in the set are disjoint. The Polygon_set_2 class also provides access functions for accessing the polygons with holes it contains, and a few queries. The most improtant query is S.oriented_side(q), which determined whether the query point $$q is contained in the interior of the set $$S, lies on the boundary of the set, or neither.

The General_polygon_set_2 class defines the predicate do_intersect() and the methods complement(), intersection(), join(), difference() and symmetric_difference() as member functions. The operands to these functions may be simple polygons (Polygon_2 object), polygons with holes (General_polygon_with_holes_2 objects), or polygon sets (General_polygon_set_2 objects). Thus, each of the function mentioned above is actually realized by a set overriding member functions.

Member functions of the General_polygon_set_2 that perform Boolean set-operations come in two flavors: for example, S.join(P, Q) computes the union of $$P and $$Q and assigned the reuslt to $$S, while S.join(P) preformes the operation $$S S P. Similarly, S.complement(P) sets $$S to be the complement of $$P, while $$S.complement() simply negates the set $$S.

A Sequence of Set Operations

The free functions reviewed in Section 12.2.1 serve as a wrapper for the polygon-set class, and are only provided for convinience. A typical such function constructs a pair of General_polygon_set_2 objects, invokes the appropriate method to apply the desired Boolean operation, and transforms the resulting polygon set to the required output format. Thus, when several operations are performed in a sequence, it is much more efficient to use the member functions of the General_polygon_set_2 type directly, as the extraction of the polygons from the internal representation for some operation, and the reconstruction of the internal representation for the succeeding operation could be time consuming.

//! \file examples/Boolean_set_operations_2/ex_sequence.C
// Performing a sequence of Boolean set-operations.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Polygon_2.h>
#include <CGAL/Polygon_with_holes_2.h>
#include <CGAL/Polygon_set_2.h>

#include <list>

typedef CGAL::Cartesian<Number_type>               Kernel;
typedef Kernel::Point_2                            Point_2;
typedef CGAL::Polygon_2<Kernel>                    Polygon_2;
typedef CGAL::Polygon_with_holes_2<Kernel>         Polygon_with_holes_2;
typedef CGAL::Polygon_set_2<Kernel>                Polygon_set_2;

#include "print_utils.h"

int main ()
{
  // Construct the two initial polygons and the clipping rectangle.
  Polygon_2 P;
  P.push_back (Point_2 (0, 1));
  P.push_back (Point_2 (2, 0));
  P.push_back (Point_2 (1, 1));
  P.push_back (Point_2 (2, 2));

  Polygon_2 Q;
  Q.push_back (Point_2 (3, 1));
  Q.push_back (Point_2 (1, 2));
  Q.push_back (Point_2 (2, 1));
  Q.push_back (Point_2 (1, 0));

  Polygon_2 rect;
  rect.push_back (Point_2 (0, 0));
  rect.push_back (Point_2 (3, 0));
  rect.push_back (Point_2 (3, 2));
  rect.push_back (Point_2 (0, 2));
  
  // Perform a sequence of operations.
  Polygon_set_2 S;
  S.insert (P);
  S.join (Q);                   // Compute the union of P and Q.
  S.complement();               // Compute the complement.
  S.intersection (rect);        // Intersect with the clipping rectangle.
  
  // Print the result.
  std::list<Polygon_with_holes_2> res;
  std::list<Polygon_with_holes_2>::const_iterator it;

  std::cout << "The result contains " << S.number_of_polygons_with_holes() 
            << " components:" << std::endl;

  S.polygons_with_holes (std::back_inserter (res));
  for (it = res.begin(); it != res.end(); ++it) {
    std::cout << "--> ";
    print_polygon_with_holes (*it);
  }
  
  return 0;
}

Inserting Non Intersecting Polygons

If you want to compute the union of a polygon $$P ($$P may be a simple polygon or a polygon-with-holes object) with a general-polygon set $$R, and store the result in $$R, you can construct a polygon set $$S(P), and apply the union operation as follows:

  General_polygon_2 S (P);
  R.join (S);

As a matter of fact, you can apply the union operation directly:

  R.join (P);

However, if you know that the polygon does not intersect any one of the polygons represented by $$R, you can use the more efficient method insert():

  R.insert (P);

As insert() assumes that $$P R = , it does not try to compute intersections between the boundaries of $$P and of $$R. This fact significantly speeds up the insertion process in comparison with the insertion of a non-disjoint polygon that intersects $$R.

The insert() function is also overloaded, so it can also accept a range of polygons. When a range of polygons are inserted into a polygon set $$S, all the polygons in the range and the polygons represented by $$S must be pairwise disjoint in their interiors.

12.2.3   Performing Aggregated Operations

There are a few options to compute the union of a set of polygons $$P₁, ...P_m. You can do it incrementally as follows. At each step compute the union of $$S_k-1 = _i=1^k-1P_i with $$P_k and obtain $$S_k. Namely, if the polygon set is given as a pair of iterator [begin, end), the following loop computes their union in $$S.

  InputIterator iter = begin;
  Polygon_set_2 S (*iter);

  while (++iter != end) {
    S.join (*iter);
    ++iter;
  }

S₁ S₂

_i=1^mP_i

Our package provides the free overloaded functions join() and intersect() that aggregately compute the union and the intersection of a range of input polygons. There is no restriction on the polygons in the range - naturally, they may intersect each other. The package provides the overloaded free function do_intersect(begin, end) that determines whether the polygons in the range defined by the two input iterators [begin, end) intersect.

The class General_polygon_set_2 also provides equivalent member functions that aggragately operate on a range of input polygons or polygons with holes. When such a member function is called, the general polygons represented by the current object are considered operands as well. Thus, you can easily compute the union of our polygon range as follows:

  Polygon_set_2 S;
  S.join (begin, end);

12.3   Boolean Set-Operations on General Polygons

Using the topological terminology, a general polygon can represent any simply-connected point set whose boundary is a strictly simple curve. Such a polygon is a model of the GeneralPolygon_2 concept. A model of this concept must fulfill the following requirements:

• A general polygon is constructible from a range of pairwise interior disjoint $$x-monotone curves $$c₁, ..., c_n. The target point of the $$kth curve $$c_k and the source point of the next curve in the range (in a cyclic order) must coincide, such that this point defines the $$kth polygon vertex.
• It is possible to traverse the $$x-monotone curves that form the edges of a general polygon.

• Construction for a general polygon that represent the outer boundary and a range of general polygons that represent the holes.
• Accessing the general polygons that represents the outer boundary (in case of a bounded set).
• Traversing the holes.

The central class-template General_polygon_set_2<Traits> is used to represent point sets that are comprised of a finite number of general polygons with holes that are pairwise disjoint, and provides various Boolean set-operations on such sets. It is parameterized by a traits class that defines the type of points used to represent polygon vertices and the type of $$x-monotone curves that represent the polygon edges. The traits class also provides primitive geometric operations that operate on objects of these types. An instatiated General_polygon_set_2 class defines the nested types General_polygon_set_2<Traits>::Polygon_2 and General_polygon_set_2<Traits>::Polygon_with_holes_2, which model the concepts GeneralPolygon_2 and GeneralPolygonWithHoles_2 respectively.

12.3.1   The Traits-Class Concepts

The traits class used to instantiate the General_polygon_set_2 class template must model the concept GeneralPolygonSetTraits_2, and is tailored to handle a specific family of curves. The concept GeneralPolygonSetTraits_2 refines the concept ArrangementDirectionalXMonotoneTraits_2 specified next.

The concept ArrangementDirectionalXMonotoneTraits_2 refines the concept ArrangementXMonotoneTraits_2 (see Section 17.4.1.2 in the 2D Arrangements chapter). Thus, a model of this concept must define the type X_monotone_curve_2, which represents an $$x-monotone curve, and the type Point_2, with represents a planar point. Such a point may be an endpoint of an $$x-monotone curve or an intersection point between two curves. It must also provide various geometric predicates and operations on these types listed by the base concept, such as determining whether a point lies above or below an $$x-monotone curve, computing the intersections between two curves, etc. Note that the base concept does not assume that $$x-monotone curves are directed: an $$x-monotone curve is not required to have a designated source and target, it is only required to determine the left (lexicographically smaller) and the right (lexicographically larger) endpoints of a given curve.

The ArrangementDirectionalXMonotoneTraits_2 concept treats its $$x-monotone curves as directed objects. It thus requires two additional operations on $$x-monotone curves:

• Given an $$x-monotone curve, compare its source and target points lexicographically.
• Given an $$x-monotone curve, construct its opposite curve (namely, swap its source and target points).

The traits classes Arr_segment_traits_2, Arr_non_caching_segment_traits, Arr_circle_segment_traits_2, Arr_conic_traits_2 and Arr_rational_arc_traits_2, which are bundeled in the Arrangement_2 package and distributed with CGAL, are all models of the refined concept ArrangementDirectionalXMonotoneTraits_2.³

Just as with the case of computations using models of the ArrangementXMonotoneTraits_2 concept, operations are robust only when exact arithmetic is used. When inexact arithmetic is used, (nearly) degenerate configurations may result in abnormal termination of the program or even incorrect results.

12.3.2   Operating on Polygons with Circular Arcs

Two traits classes are distributed with CGAL. The first one is named Gps_segment_traits_2, and it is used to perform Boolean set-operations on oridnary polygons and polygons with holes. In fact, the class Polygon_set_2 introduced in Section 12.2.2 is a specialization of General_polygon_set_2<Gps_segment_traits_2>. This class defined its polygon and polygon with holes types, such that the usage of this traits class is encapsulated in the polygon-set class.

The other predefined traits class is named Gps_circle_segment_traits_2<Kernel> and is parameterized by a geometric CGAL kernel. By instantiating the General_polygon_set_2 with this traits class, we obtain the representation of a polygon whose boundary may be comprised of line segments and circular arcs. The circle-segment traits class provides predicates and constructions on non-linear objects; yet, it uses only rational arithmetic and is very efficient as a consequence.

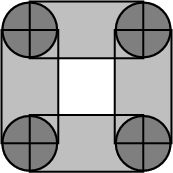
//! \file examples/Boolean_set_operations_2/ex_circle_segment.C
// Handling circles and linear segments concurrently.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Gps_circle_segment_traits_2.h>
#include <CGAL/General_polygon_set_2.h>
#include <CGAL/General_polygon_with_holes_2.h>
#include <CGAL/Lazy_exact_nt.h>

#include <list>

typedef CGAL::Lazy_exact_nt<Number_type>                Lazy_exact_nt;
typedef CGAL::Cartesian<Lazy_exact_nt>                  Kernel;
typedef Kernel::Point_2                                 Point_2;
typedef Kernel::Circle_2                                Circle_2;
typedef CGAL::Gps_circle_segment_traits_2<Kernel>       Traits_2;

typedef CGAL::General_polygon_set_2<Traits_2>           Polygon_set_2;
typedef Traits_2::Polygon_2                             Polygon_2;
typedef Traits_2::Polygon_with_holes_2                  Polygon_with_holes_2;
typedef Traits_2::Curve_2                               Curve_2;
typedef Traits_2::X_monotone_curve_2                    X_monotone_curve_2;

// Construct a polygon from a circle.
Polygon_2 construct_polygon (const Circle_2& circle)
{
  // Subdivide the circle into two x-monotone arcs.
  Traits_2 traits;
  Curve_2 curve (circle);
  std::list<CGAL::Object>  objects;
  traits.make_x_monotone_2_object() (curve, std::back_inserter(objects));
  CGAL_assertion (objects.size() == 2);

  // Construct the polygon.
  Polygon_2 pgn;
  X_monotone_curve_2 arc;
  std::list<CGAL::Object>::iterator iter;

  for (iter = objects.begin(); iter != objects.end(); ++iter) {
    CGAL::assign (arc, *iter);
    pgn.push_back (arc);
  }

  return pgn;
}

// Construct a point from a rectangle.
Polygon_2 construct_polygon (const Point_2& p1, const Point_2& p2,
                             const Point_2& p3, const Point_2& p4)
{
  Polygon_2 pgn;
  X_monotone_curve_2 s1(p1, p2);    pgn.push_back(s1);
  X_monotone_curve_2 s2(p2, p3);    pgn.push_back(s2);
  X_monotone_curve_2 s3(p3, p4);    pgn.push_back(s3);
  X_monotone_curve_2 s4(p4, p1);    pgn.push_back(s4);
  return pgn;
}

// The main program:
int main ()
{
  // Insert four non-intersecting circles.
  Polygon_set_2 S; 
  Polygon_2 circ1, circ2, circ3, circ4;

  circ1 = construct_polygon(Circle_2(Point_2(1, 1), 1));  S.insert(circ1);
  circ2 = construct_polygon(Circle_2(Point_2(5, 1), 1));  S.insert(circ2);
  circ3 = construct_polygon(Circle_2(Point_2(5, 5), 1));  S.insert(circ3);
  circ4 = construct_polygon(Circle_2(Point_2(1, 5), 1));  S.insert(circ4);
  
  // Compute the union with four rectangles incrementally.
  Polygon_2 rect1, rect2, rect3, rect4;

  rect1 = construct_polygon(Point_2(1, 0), Point_2(5, 0),
                            Point_2(5, 2), Point_2(1, 2));
  S.join (rect1);

  rect2 = construct_polygon(Point_2(1, 4), Point_2(5, 4),
                            Point_2(5, 6), Point_2(1, 6));
  S.join (rect2);

  rect3 = construct_polygon(Point_2(0, 1), Point_2(2, 1), 
                            Point_2(2, 5), Point_2(0, 5));
  S.join (rect3);

  rect4 = construct_polygon(Point_2(4, 1), Point_2(6, 1), 
                            Point_2(6, 5), Point_2(4, 5));
  S.join (rect4);

  // Print the output.
  std::list<Polygon_with_holes_2> res;
  S.polygons_with_holes (std::back_inserter (res));

  std::copy (res.begin(), res.end(),
             std::ostream_iterator<Polygon_with_holes_2>(std::cout, "\n"));
  std::cout << std::endl;
  
  return 0;
}

12.3.3   General Polygon Set Traits Adapter

The concept GeneralPolygon_2 and its generic model General_polygon_2<ArrDirectionalXMonotoneTraits> facilitate the production of general-polygon set traits classes. A model of the concept GeneralPolygon_2 represents a simple point-set in the plane bounded by $$x-monotone curves. As opposed to the plain Traits::Polygon_2 type defined by any traits class, it must define the type X_monotone_curve_2, which represents an $$x-monotone curve of the point-set boundary. It must provide a constructor from a range of such curves, and a pair of methods, namely curves_begin() and curves_end(), that can be used to iterate over the point-set boundary curves.

The class-template General_polygon_2<ArrDirectionalXMonotoneTraits> models the concept GeneralPolygon_2. Its template parameter must be instantiated with a model of the concept ArrangementDirectionalXMonotoneTraits_2 from which it obtains the X_monotone_curve_2 type, and it uses the necessary operations on this type provided by such a model to maintain a container of directed curves of type X_monotone_curve_2, which represents the boundary of the general polygon.

The class-template Gps_traits_2<ArrDirectionalXMonotoneTraits,GeneralPolygon> models the concept GeneralPolygonSetTraits_2. Its implementation is rather simple, as it is derived from the instantiated template-parameter ArrXMonotoneTraits_2 inheriting its necessary types and methods, and it exploits the methods provided by the instantiated parameter GeneralPolygon - a model of the concept GeneralPolygon_2. By default, the GeneralPolygon parameter is defined as General_polygon_2<ArrangementDirectionalXMonotoneTraits_2>

The code excerpt listed below defines a general-polygon set type that can be used to perform Boolean set-operations on point sets bounded by linear segments used by the Arrangement_2 class by default. A model of the GeneralPolygon_2 concept that represents a (linear) polygon bounded by curves of type Arr_segment_2 is generated. The later is obtained from the instantiated parameter Arr_segment_traits_2, which defines Arr_segment_2 to be its exposed type X_monotone_curve_2.

typedef CGAL::Gmpq                              	   Number_type;
typedef CGAL::Cartesian<Number_type>            	   Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel>      	   Arr_traits_2;
typedef CGAL::General_polygon_2<Arr_traits_2>   	   General_polygon_2;
typedef CGAL::Gps_traits_2<Arr_traits_2,General_polygon_2> Traits_2;
typedef CGAL::General_polygon_set_2<Traits_2>              General_polygon_set_2;

//! \file examples/Boolean_set_operations_2/ex_traits_adaptor.C
// Using the traits adaptor to generate a traits of conics.
#include <CGAL/basic.h>

#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
  std::cout << "Sorry, this example needs CORE ..." << std::endl; 
  return (0);
}
#else

#include <CGAL/Cartesian.h>
#include <CGAL/CORE_algebraic_number_traits.h>
#include <CGAL/Arr_conic_traits_2.h>
#include <CGAL/General_polygon_2.h>
#include <CGAL/General_polygon_with_holes_2.h>
#include <CGAL/Gps_traits_2.h>
#include <CGAL/Boolean_set_operations_2.h>

#include <list>

typedef CGAL::CORE_algebraic_number_traits              Nt_traits;
typedef Nt_traits::Rational                             Rational;
typedef Nt_traits::Algebraic                            Algebraic;
typedef CGAL::Cartesian<Rational>                       Rat_kernel;
typedef CGAL::Cartesian<Algebraic>                      Alg_kernel;
typedef CGAL::Arr_conic_traits_2<Rat_kernel,
                                 Alg_kernel,Nt_traits>  Conic_traits_2;
typedef CGAL::General_polygon_2<Conic_traits_2>         Polygon_2;
typedef CGAL::Gps_traits_2<Conic_traits_2, Polygon_2>   Traits_2;
typedef Traits_2::Polygon_with_holes_2                  Polygon_with_holes_2;
typedef Traits_2::Curve_2                               Curve_2;
typedef Traits_2::X_monotone_curve_2                    X_monotone_curve_2;
typedef Traits_2::Point_2                               Point_2;

// Insert a conic arc as a polygon edge: Subdivide the arc into x-monotone
// sub-arcs and append these sub-arcs as polygon edges.
void append_conic_arc (Polygon_2& polygon, const Curve_2& arc)
{
  Conic_traits_2                    traits;
  std::list<CGAL::Object>           objects;
  std::list<CGAL::Object>::iterator it;
  X_monotone_curve_2                xarc;

  traits.make_x_monotone_2_object() (arc, std::back_inserter(objects));
  for (it = objects.begin(); it != objects.end(); ++it)
  {
    if (CGAL::assign (xarc, *it))
      polygon.push_back (xarc);
  }
}

int main ()
{
  // Construct a parabolic arc supported by a parabola: x^2 + 2y - 4 = 0,
  // and whose endpoints lie on the line y = 0:
  Curve_2 parabola1 = Curve_2 (1, 0, 0, 0, 2, -4, CGAL::COUNTERCLOCKWISE,
                               Point_2(2, 0), Point_2(-2, 0));

  // Construct a parabolic arc supported by a parabola: x^2 - 2y - 4 = 0,
  // and whose endpoints lie on the line y = 0:
  Curve_2 parabola2 = Curve_2 (1, 0, 0, 0, -2, -4, CGAL::COUNTERCLOCKWISE,
                               Point_2(-2, 0), Point_2(2, 0));
  
  // Construct a polygon from these two parabolic arcs.
  Polygon_2 P;
  append_conic_arc (P, parabola1);
  append_conic_arc (P, parabola2);

  // Construct a polygon that corresponds to the ellipse: x^2 + 9y^2 - 9 = 0:
  Polygon_2 Q;
  append_conic_arc (Q, Curve_2 (-1, -9, 0, 0, 0, 9));

  // Compute the intersection of the two polygons.
  std::list<Polygon_with_holes_2> res;
  CGAL::intersection (P, Q, std::back_inserter(res));

  std::copy (res.begin(), res.end(),       // export to standard output
             std::ostream_iterator<Polygon_with_holes_2>(std::cout, "\n"));
  std::cout << std::endl;
  
  return (0);
}

#endif

12.3.4   Example - Aggregated Operations

In Section 12.2.3 we describe how aggragated union and intersection operations can be applied to a collection of ordinary polygons or polygons with holes. Naturally, the aggregated operations can be applied also to collections of general polygons. As was the case with ordinary polygons, using aggregated operations is recommended when the number of intersections of the input polygons is of the same order of magnitude as the complexity of the result. If this is not the case, computing the result incrementally may prove faster.

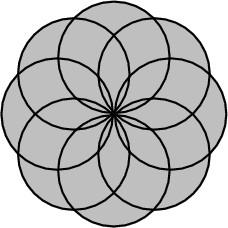
//! \file examples/Boolean_set_operations_2/ex_set_union.C
// Computing the union of a set of circles.

#include "bso_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Gps_circle_segment_traits_2.h>
#include <CGAL/Boolean_set_operations_2.h>
#include <CGAL/Lazy_exact_nt.h>

#include <list>
#include <stdlib.h>
#include <math.h>

typedef CGAL::Lazy_exact_nt<Number_type>                Lazy_exact_nt;
typedef CGAL::Cartesian<Lazy_exact_nt>                  Kernel;
typedef Kernel::Point_2                                 Point_2;
typedef Kernel::Circle_2                                Circle_2;
typedef CGAL::Gps_circle_segment_traits_2<Kernel>       Traits_2;

typedef CGAL::General_polygon_set_2<Traits_2>           Polygon_set_2;
typedef Traits_2::Polygon_2                             Polygon_2;
typedef Traits_2::Polygon_with_holes_2                  Polygon_with_holes_2;
typedef Traits_2::Curve_2                               Curve_2;
typedef Traits_2::X_monotone_curve_2                    X_monotone_curve_2;

// Construct a polygon from a circle.
Polygon_2 construct_polygon (const Circle_2& circle)
{
  // Subdivide the circle into two x-monotone arcs.
  Traits_2 traits;
  Curve_2 curve (circle);
  std::list<CGAL::Object> objects;
  traits.make_x_monotone_2_object() (curve, std::back_inserter(objects));
  CGAL_assertion (objects.size() == 2);

  // Construct the polygon.
  Polygon_2 pgn;
  X_monotone_curve_2 arc;
  std::list<CGAL::Object>::iterator iter;

  for (iter = objects.begin(); iter != objects.end(); ++iter) {
    CGAL::assign (arc, *iter);
    pgn.push_back (arc);
  }

  return pgn;
}

// The main program:
int main (int argc, char * argv[])
{
  // Read the number of circles from the command line.
  unsigned int n_circles = 8;
  if (argc > 1) n_circles = atoi(argv[1]);

  // Create the circles, equally spaced of the circle x^2 + y^2 = 1.
  const double pi = std::atan(1.0) * 4;
  const double n_circles_reciep = 1.0 / n_circles;
  const double radius = 1;
  const double frac = 2 * pi * n_circles_reciep;
  std::list<Polygon_2> circles;
  unsigned int k;
  for (k = 0; k < n_circles; k++) {
    const double angle = frac * k;
    const double x = radius * std::sin(angle);
    const double y = radius * std::cos(angle);
    Point_2 center = Point_2(x, y);
    Circle_2 circle(center, radius);

    circles.push_back (construct_polygon (circle));
  }
  
  // Compute the union aggragately.
  std::list<Polygon_with_holes_2> res;
  CGAL::join (circles.begin(), circles.end(), std::back_inserter (res));

  // Print the result.
  std::copy (res.begin(), res.end(),
             std::ostream_iterator<Polygon_with_holes_2>(std::cout, "\n"));
  std::cout << std::endl;
  
  return 0;
}

Footnotes

1	A continuous planar curve $$C is $$x-monotone if every vertical line intersects it at most once. We also allow vertical line segments, which are considered weakly $$x-monotone.
2	The function that computes the union of two polygons is called join(), since the word union is reserved in C++.
3	The Arr_polyline_traits_2 class is not a model of the, ArrangementDirectionalXMonotoneTraits_2 concept, as the $$x-monotone curve it defines is always directed from left to right. Thus, an opposite curve cannot be constructed. However, it is not very useful to construct a polygon whose edges are polylines, as an ordinary polygon with linear edges can represent the same entity.