Many geometric data structures can be interpreted as graphs, as they consist of vertices, edges and faces. This is the case for the halfedge data structure, for the polyhedron, for arrangements and for triangulations. With means of duality one can also interpret faces as vertices and edges between adjacent faces as edges of the dual graph.
As the scope of CGAL is geometry and not graph algorithms, we provide the necessary classes and functions that allow to use the algorithms of the Boost Graph Library (BGL) [SLL02] for CGAL data structures.
60.1 A Short Introduction to the Boost Graph Library
The algorithms of the BGL operate on models of the various graph concepts. The traits class boost::graph_traits allows the algorithms to determine the types of vertices and edges. Free functions that operator on graphs allow the algorithms to obtain, for example, the source vertex of an edge, or all edges incident to a vertex. The algorithms use property maps to associate information to vertices and edges. The algorithms allow visitors to register callbacks that will be called during the execution of the algorithms. Finally, the graph algorithms use the named parameter mechanism, which allows to pass the arguments in arbitrary order.
Graph Concepts
The BGL introduces several graph concepts, which have different sets of characteristics and requirements, as for example whether one can enumerate all vertices or all edges, whether one only can get the outgoing edges of a vertex, or also the ingoing edges, or whether one can add and remove vertices and edges or not.
Graph concepts in the BGL manual: http://www.boost.org/libs/graph/doc/graph_concepts.html
The Graph Traits Class
The algorithms determine types with the help of the traits class boost::graph_traits. Such types are the vertex_descriptor which is equivalent to a vertex handle in CGAL data structures, the vertex_iterator which is similar to the vertex iterators in CGAL data structures, and the out_edge_iterator which is similar to edge circulators, which allow to enumerate the edges incident to a vertex. The latter two are similar and not equivalent, because their value type is a vertex_descriptor, whereas in CGAL handles, iterators, and cicrulators all have the same value type, namely the vertex type. Given a graph type G the declaration of a vertex descriptor looks as follows: boost::graph_traits<G>::vertex_descriptor vd;.
The graph traits in the BGL manual: http://www.boost.org/libs/graph/doc/graph_traits.html
Free Functions for Exploring a Graph
The algorithms obtain incidence information with the help of global functions like pair<vertex_iterator,vertex_iterator> vertices(const Graph& g); for getting an iterator range which allows to enumerate all vertices, or int num_vertices(const Graph&); for getting the number of vertices of a graph, or vertex_descriptor source(edge_descriptor, const Graph&, for getting the source vertex of an edge. Note, that the way we have written the types is a simplification, that is in reality the signature of the first of the above functions is pair<boost::graph_traits<Graph>::vertex_iterator,boost::graph_traits<Graph>::vertex_iterator> vertices(const Graph& g);.
The free functions required for graph concepts: http://www.boost.org/libs/graph/doc/graph_concepts.html
Property Maps
Another feature used heavily in the BGL is the property map which is offered by the Boost Property Map Library. Property maps are used to attach information to vertices and edges. It is again a traits class and some free functions for obtaining the property map from a graph, and for getting and putting properties.
The free functions are get and put. The first one is overloaded. One version allows to obtain a property map for a given property tag. For example m = get(g, boost::vertex_index) gives us a property map that associates an index in the range [0, num_vertices(g)) to each vertex descriptor of the graph. The second version of the get function allows to read it as follows for a vertex descriptor vd: int vdi = get(m, vd). Just as get allows to read data, put allows to write them. For example, the Dijksta's shortest path algorithm writes the predecessor of each vertex, as well as the distance to the source in such a property map.
The data themselves may be stored in the vertex or edge, or they may be stored in an external data structure, or they may be computed on the fly. This is an ``implementation detail'' of the particular property map.
Property maps in the Boost manuals: http://www.boost.org/libs/property_map/property_map.html
Visitors
Visitors are ojects that provide functions that get called at specified event points by the algorithm they visit. The notion of visitors is a design pattern, and also used in CGAL, e.g., the Arr_observer<Arrangement> in the arrangement package.
The functions as well as the event points are library specific. Event points in graph algorithms are, for example, when a vertex is traversed the first time, or when all outgoing edges of a vertex are traversed.
Visitors in the BGL manual: http://www.boost.org/libs/graph/doc/visitor_concepts.html
Named Parameters
The algorithms of the BGL often have many parameters. Although the default value is most often appropriate, one has to write them explicitly, if one only wants to deviate from the default for the last one. The solution to this problem is to first write a tag and then the parameter, which for Dijkstra's shortest path algorithm, might look as follows:
std::vector<vertex_descriptor> p(num_vertices(g)); std::vector<int> d(num_vertices(g)); vertex_descriptor s = vertex(A, g); dijkstra_shortest_paths(g, s, predecessor_map(&p[0]).distance_map(&d[0]));
The named parameters in the example use the tags predecessor_map and distance_map and they are concatenated with the dot operator.
Named parameters in the BGL manual: http://www.boost.org/libs/graph/doc/bgl_named_params.html
60.2 Extensions of the BGL
CGAL provides the partial specializations and free functions such that several data structures become model of some of the BGL graph concepts. Furthermore, we define the new graph concept HalfedgeGraph, a traits class halfedge_graph_traits, and free functions for accessing opposite edges as well as the clockwise and counterclockwise neighbor of an edge around a given vertex.
These extensions are used by the surface simplification algorithms which follow the design of the BGL as sketched in the previous section.
60.3 Header Files, Namespaces, and Naming Conventions
As we interface two libraries we have to explain what resides in which namespace, and what naming conventions we apply to what.
Partial specializations of the boost::graph_traits<Graph> for the CGAL package Package are in the namespace boost and in the headerfile <CGAL/boost/graph/graph_traits_Package.h>.
The halfedge_graph_traits class is in the namespace CGAL, but it is not capitalized as the boost::graph_traits is not. The same holds for the types and enums for vertex and edge properties.
60.4 Polyhedral Surfaces as Model of the Boost Graph Concept
The class Polyhedron_3 is model of the graph concept. Furthermore this chapter introduces a new graph concept, the HalfedgeGraph.
60.4.1 Example: Minimum Spanning Tree of a Polyhedral Surface
The example code computes the minimum spanning tree on a polyhedral surface. More examples can be found in Chapter 42 on surface mesh simplification.
File: examples/BGL_polyhedron_3/kruskal.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/boost/graph/graph_traits_Polyhedron_3.h>
#include <CGAL/boost/graph/properties_Polyhedron_3.h>
#include <iostream>
#include <list>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
typedef CGAL::Cartesian<double> Kernel;
typedef Kernel::Vector_3 Vector;
typedef Kernel::Point_3 Point;
typedef CGAL::Polyhedron_3<Kernel> Polyhedron;
typedef boost::graph_traits<Polyhedron>::vertex_descriptor vertex_descriptor;
typedef boost::graph_traits<Polyhedron>::vertex_iterator vertex_iterator;
typedef boost::graph_traits<Polyhedron>::edge_descriptor edge_descriptor;
// The BGL makes heavy use of indices associated to the vertices
// We use a std::map to store the index
namespace CGAL
{
// we define operator < for handles as is not predefined
bool operator< ( vertex_descriptor x, vertex_descriptor y )
{
return &*x < &*y ;
}
} // namespace CGAL
typedef std::map<vertex_descriptor,int> VertexIndexMap;
VertexIndexMap vertex_id_map;
// A std::map is not a property map, because it is not lightweight
typedef boost::associative_property_map<VertexIndexMap> VertexIdPropertyMap;
VertexIdPropertyMap vertex_index_pmap(vertex_id_map);
void
kruskal(const Polyhedron& P)
{
// associate indices to the vertices
{
vertex_iterator vb, ve;
int index = 0;
// boost::tie assigns the first and second element of the std::pair
// returned by boost::vertices to the variables vit and ve
for(boost::tie(vb,ve)=boost::vertices(P); vb!=ve; ++vb ){
vertex_descriptor vd = *vb;
vertex_id_map[vd]= index++;
}
}
// We use the default edge weight which is the squared length of the edge
// This property map is defined in graph_traits_Polyhedron_3.h
// In the function call you can see a named parameter: vertex_index_map
std::list<edge_descriptor> mst;
boost::kruskal_minimum_spanning_tree(P,
std::back_inserter(mst),
boost::vertex_index_map(vertex_index_pmap) );
std::cout << "#VRML V2.0 utf8\n"
"Shape {\n"
"appearance Appearance {\n"
"material Material { emissiveColor 1 0 0}}\n"
"geometry\n"
"IndexedLineSet {\n"
"coord Coordinate {\n"
"point [ \n";
vertex_iterator vb, ve;
for(boost::tie(vb,ve) = boost::vertices(P); vb!=ve; ++vb){
std::cout << (*vb)->point() << "\n";
}
std::cout << "]\n"
"}\n"
"coordIndex [\n";
for(std::list<edge_descriptor>::iterator it = mst.begin(); it != mst.end(); ++it)
{
edge_descriptor e = *it ;
vertex_descriptor s = boost::source(e,P);
vertex_descriptor t = boost::target(e,P);
std::cout << vertex_id_map[s] << ", " << vertex_id_map[t] << ", -1\n";
}
std::cout << "]\n"
"}#IndexedLineSet\n"
"}# Shape\n";
}
int main() {
Polyhedron P;
Point a(1,0,0);
Point b(0,1,0);
Point c(0,0,1);
Point d(0,0,0);
P.make_tetrahedron(a,b,c,d);
kruskal(P);
return 0;
}
60.4.2 Example: Using Vertices, and Edges with an ID
The following example program shows a call to the BGL
Kruskal's minimum spanning tree algorithm accessing the id()
field stored in a Polyhedron vertex.
The main function illustrates the access to the id() field.
File: examples/BGL_polyhedron_3/kruskal_with_stored_id.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/Polyhedron_items_with_id_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/boost/graph/graph_traits_Polyhedron_3.h>
#include <CGAL/boost/graph/properties_Polyhedron_3.h>
#include <iostream>
#include <list>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
typedef CGAL::Cartesian<double> Kernel;
typedef Kernel::Point_3 Point;
typedef CGAL::Polyhedron_3<Kernel,CGAL::Polyhedron_items_with_id_3> Polyhedron;
typedef boost::graph_traits<Polyhedron>::vertex_descriptor vertex_descriptor;
typedef boost::graph_traits<Polyhedron>::vertex_iterator vertex_iterator;
typedef boost::graph_traits<Polyhedron>::edge_descriptor edge_descriptor;
void
kruskal( const Polyhedron& P)
{
// We use the default edge weight which is the squared length of the edge
// This property map is defined in graph_traits_Polyhedron_3.h
// This function call requires a vertex_index_map named parameter which
// when ommitted defaults to "get(vertex_index,graph)".
// That default works here because the vertex type supports the "id()"
// field which is used by the vertex_index internal property.
std::list<edge_descriptor> mst;
boost::kruskal_minimum_spanning_tree(P,std::back_inserter(mst));
std::cout << "#VRML V2.0 utf8\n"
"Shape {\n"
"appearance Appearance {\n"
"material Material { emissiveColor 1 0 0}}\n"
"geometry\n"
"IndexedLineSet {\n"
"coord Coordinate {\n"
"point [ \n";
vertex_iterator vb, ve;
for(boost::tie(vb,ve) = boost::vertices(P); vb!=ve; ++vb){
std::cout << (*vb)->point() << "\n";
}
std::cout << "]\n"
"}\n"
"coordIndex [\n";
for(std::list<edge_descriptor>::iterator it = mst.begin(); it != mst.end(); ++it){
std::cout << boost::source(*it,P)->id()
<< ", " << boost::target(*it,P)->id() << ", -1\n";
}
std::cout << "]\n"
"}#IndexedLineSet\n"
"}# Shape\n";
}
int main() {
Polyhedron P;
Point a(1,0,0);
Point b(0,1,0);
Point c(0,0,1);
Point d(0,0,0);
P.make_tetrahedron(a,b,c,d);
// associate indices to the vertices using the "id()" field of the vertex.
vertex_iterator vb, ve;
int index = 0;
// boost::tie assigns the first and second element of the std::pair
// returned by boost::vertices to the variables vit and ve
for(boost::tie(vb,ve)=boost::vertices(P); vb!=ve; ++vb ){
vertex_descriptor vd = *vb;
vd->id() = index++;
}
kruskal(P);
return 0;
}
60.5 Triangulations as Models of the Boost Graph Concept
Triangulations have vertices and faces. Edges are pairs of a face and the index of the edge. Particular care has to be taken with the infinite vertex, and its incident edges. One can either use a boost::filtered_graph, which makes the infinite edges invisible, or one can have a property map that returns an infinite length for these edges.
A classical example for an algorithm that is a combination of computational geometry and graph theory is the Euclidean Minimum Spanning Tree for a point set in the plane. It can be computed by running the minimum spanning tree algorithm on a Delaunay triangulation of the point set.
60.5.1 Example: Euclidean Minimum Spanning Tree
In the following example we create a Delaunay triangulation and run Kruskal's minimum spanning tree algorithm on it. Because the vertex handles of the triangulation are not indices in an array, we have to provide a property map that maps vertex handles to int's in the range [0, t.number_of_vertices()).
File: examples/BGL_triangulation_2/emst.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/boost/graph/graph_traits_Delaunay_triangulation_2.h>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
#include <boost/graph/filtered_graph.hpp>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_2 Point;
typedef CGAL::Delaunay_triangulation_2<K> Triangulation;
// As we only consider finite vertices and edges
// we need the following filter
template <typename T>
struct Is_finite {
const T* t_;
Is_finite()
: t_(NULL)
{}
Is_finite(const T& t)
: t_(&t)
{ }
template <typename VertexOrEdge>
bool operator()(const VertexOrEdge& voe) const {
return ! t_->is_infinite(voe);
}
};
typedef Is_finite<Triangulation> Filter;
typedef boost::filtered_graph<Triangulation,Filter,Filter> Finite_triangulation;
typedef boost::graph_traits<Finite_triangulation>::vertex_descriptor vertex_descriptor;
typedef boost::graph_traits<Finite_triangulation>::vertex_iterator vertex_iterator;
typedef boost::graph_traits<Finite_triangulation>::edge_descriptor edge_descriptor;
// The BGL makes use of indices associated to the vertices
// We use a std::map to store the index
typedef std::map<vertex_descriptor,int> VertexIndexMap;
VertexIndexMap vertex_id_map;
// A std::map is not a property map, because it is not lightweight
typedef boost::associative_property_map<VertexIndexMap> VertexIdPropertyMap;
VertexIdPropertyMap vertex_index_pmap(vertex_id_map);
int
main(int,char*[])
{
Triangulation t;
Filter is_finite(t);
Finite_triangulation ft(t, is_finite, is_finite);
Point p ;
while(std::cin >> p){
t.insert(p);
}
vertex_iterator vit, ve;
// Associate indices to the vertices
int index = 0;
// boost::tie assigns the first and second element of the std::pair
// returned by boost::vertices to the variables vit and ve
for(boost::tie(vit,ve)=boost::vertices(ft); vit!=ve; ++vit ){
vertex_descriptor vd = *vit;
vertex_id_map[vd]= index++;
}
// We use the default edge weight which is the squared length of the edge
// This property map is defined in graph_traits_Triangulation_2.h
// In the function call you can see a named parameter: vertex_index_map
std::list<edge_descriptor> mst;
boost::kruskal_minimum_spanning_tree(t,
std::back_inserter(mst),
vertex_index_map(vertex_index_pmap));
std::cout << "The edges of the Euclidean mimimum spanning tree:" << std::endl;
for(std::list<edge_descriptor>::iterator it = mst.begin(); it != mst.end(); ++it){
edge_descriptor ed = *it;
vertex_descriptor svd = boost::source(ed,t);
vertex_descriptor tvd = boost::target(ed,t);
Triangulation::Vertex_handle sv = svd;
Triangulation::Vertex_handle tv = tvd;
std::cout << "[ " << sv->point() << " | " << tv->point() << " ] " << std::endl;
}
return 0;
}
60.5.2 Example: Storing the Vertex ID in the Vertex
The algorithms of the BGL extensively use of the indices of vertices. In the previous example we stored the index in a std::map and turned that map in a property map. This property map was then passed as argument to the shortest path function.
If the user does not pass explicitly a property map, the graph algorithms use the property map returned by the call boost::get(boost::vertex_index,ft). This property map assumes that the vertex has a member function id() that returns a reference to an int. Therefore CGAL offers a class Triangulation_vertex_base_with_id_2. It is in the users responsibility to set the indices properly.
The example further illustrates that the graph traits also works for the Delaunay triangulation.
File: examples/BGL_triangulation_2/dijkstra_with_internal_properties.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Triangulation_vertex_base_with_id_2.h>
#include <CGAL/boost/graph/graph_traits_Delaunay_triangulation_2.h>
#include <climits>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/graph/filtered_graph.hpp>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_2 Point;
typedef CGAL::Triangulation_vertex_base_with_id_2<K> Tvb;
typedef CGAL::Triangulation_face_base_2<K> Tfb;
typedef CGAL::Triangulation_data_structure_2<Tvb,Tfb> Tds;
typedef CGAL::Delaunay_triangulation_2<K, Tds> Triangulation;
// consider finite vertices and edges.
template <typename T>
struct Is_finite {
const T* t_;
Is_finite()
: t_(NULL)
{}
Is_finite(const T& t)
: t_(&t)
{ }
template <typename VertexOrEdge>
bool operator()(const VertexOrEdge& voe) const {
return ! t_->is_infinite(voe);
}
};
typedef Is_finite<Triangulation> Filter;
typedef boost::filtered_graph<Triangulation,Filter,Filter> Finite_triangulation;
typedef boost::graph_traits<Finite_triangulation>::vertex_descriptor vertex_descriptor;
typedef boost::graph_traits<Finite_triangulation>::vertex_iterator vertex_iterator;
int
main(int,char*[])
{
Triangulation t;
Filter is_finite(t);
Finite_triangulation ft(t, is_finite, is_finite);
t.insert(Point(0,0));
t.insert(Point(1,0));
t.insert(Point(0.2,0.2));
t.insert(Point(0,1));
t.insert(Point(0,2));
vertex_iterator vit, ve;
// associate indices to the vertices
int index = 0;
for(boost::tie(vit,ve)=boost::vertices(ft); vit!=ve; ++vit ){
vertex_descriptor vd = *vit;
vd->id()= index++;
}
typedef boost::property_map<Triangulation, boost::vertex_index_t>::type VertexIdPropertyMap;
VertexIdPropertyMap vertex_index_pmap = get(boost::vertex_index, ft);
// Dijkstra's shortest path needs property maps for the predecessor and distance
std::vector<vertex_descriptor> predecessor(boost::num_vertices(ft));
boost::iterator_property_map<std::vector<vertex_descriptor>::iterator, VertexIdPropertyMap>
predecessor_pmap(predecessor.begin(), vertex_index_pmap);
std::vector<double> distance(boost::num_vertices(ft));
boost::iterator_property_map<std::vector<double>::iterator, VertexIdPropertyMap>
distance_pmap(distance.begin(), vertex_index_pmap);
vertex_descriptor source = *boost::vertices(ft).first;
std::cout << "\nStart dijkstra_shortest_paths at " << source->point() << std::endl;
boost::dijkstra_shortest_paths(ft, source ,
distance_map(distance_pmap)
.predecessor_map(predecessor_pmap));
for(boost::tie(vit,ve)=boost::vertices(ft); vit!=ve; ++vit ){
vertex_descriptor vd = *vit;
std::cout << vd->point() << " [" << vd->id() << "] ";
std::cout << " has distance = " << get(distance_pmap,vd) << " and predecessor ";
vd = get(predecessor_pmap,vd);
std::cout << vd->point() << " [" << vd->id() << "]\n";
}
return 0;
}
60.6 Arrangements as Models of the Boost Graph Concept
For the arrangements CGAL offers the graph traits for the arrangement itself as well as for its dual graph.
60.6.1 Example for the Arrangement as Graph
Arrangement instances are adapted to boost graphs by specializing the boost:graph_traits template for Arrangement_2 instances. The graph-traits states the graph concepts that the arrangement class models (see below) and defines the types required by these concepts.
In this specialization the Arrangement_2 vertices correspond to the graph vertices, where two vertices are adjacent if there is at least one halfedge connecting them. More precisely, Arrangement_2::Vertex_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. As halfedges are directed, we consider the graph to be directed as well. Moreover, as several interior-disjoint -monotone curves (say circular arcs) may share two common endpoints, inducing an arrangement with two vertices that are connected with several edges, we allow parallel edges in our boost graph.
Given an Arrangement_2 instance, we can efficiently traverse its vertices and halfedges. Thus, the arrangement graph is a model of the concepts VertexListGraph and EdgeListGraph introduced by the BGL. At the same time, we use an iterator adapter of the circulator over the halfedges incident to a vertex (Halfedge_around_vertex_circulator - see Section 24.2.2.1), so it is possible to go over the ingoing and outgoing edges of a vertex in linear time. Thus, our arrangement graph is a model of the concept BidirectionalGraph (this concept refines IncidenceGraph, which requires only the traversal of outgoing edges).
It is important to notice that the vertex descriptors we use are Vertex_handle objects and not vertex indices. However, in order to gain more efficiency in most BGL algorithm, it is better to have them indexed , where is the number of vertices. We therefore introduce the Arr_vertex_index_map<Arrangement> class-template, which maintains a mapping of vertex handles to indices, as required by the BGL. An instance of this class must be attached to a valid arrangement vertex when it is created. It uses the notification mechanism (see Section 24.7) to automatically maintain the mapping of vertices to indices, even when new vertices are inserted into the arrangement or existing vertices are removed.
In most algorithm provided by the BGL, the output is given by property maps, such that each map entry corresponds to a vertex. For example, when we compute the shortest paths from a given source vertex to all other vertices we can obtain a map of distances and a map of predecessors - namely for each vertex we have its distance from and a descriptor of the vertex that precedes in the shortest path from . If the vertex descriptors are simply indices, one can use vectors to efficiently represent the property maps. As this is not the case with the arrangement graph, we offer the Arr_vertex_property_map<Arrangement,Type> template allows for an efficient mapping of Vertex_handle objects to properties of type Type. Note however that unlike the Arr_vertex_index_map class, the vertex property-map class is not kept synchronized with the number of vertices in the arrangement, so it should not be reused in calls to BGL functions in case the arrangement is modified in between these calls.
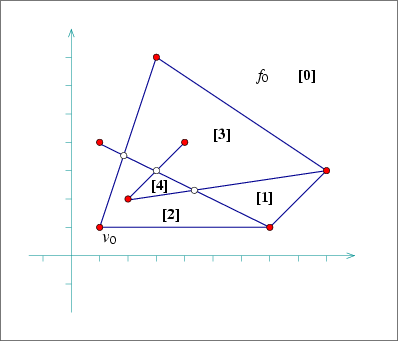
In the following example we construct an arrangement of 7 line segments, as shown in Figure 60.1, then use Dijkstra's shortest-paths algorithm from the BGL to compute the graph distance of all vertices from the leftmost vertex in the arrangement . Note the usage of the Arr_vertex_index_map and the Arr_vertex_property_map classes. The latter one, instantiated by the type double is used to map vertices to their distances from .
File: examples/BGL_arrangement_2/primal.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <climits>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <CGAL/graph_traits_Arrangement_2.h>
#include <CGAL/Arr_vertex_map.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
// A functor used to compute the length of an edge.
class Edge_length_func
{
public:
// Boost property type definitions:
typedef boost::readable_property_map_tag category;
typedef double value_type;
typedef value_type reference;
typedef Arrangement_2::Halfedge_handle key_type;
double operator() (Arrangement_2::Halfedge_handle e) const
{
const double x1 = CGAL::to_double (e->source()->point().x());
const double y1 = CGAL::to_double (e->source()->point().y());
const double x2 = CGAL::to_double (e->target()->point().x());
const double y2 = CGAL::to_double (e->target()->point().y());
const double diff_x = x2 - x1;
const double diff_y = y2 - y1;
return (std::sqrt (diff_x*diff_x + diff_y*diff_y));
}
};
double get (Edge_length_func edge_length, Arrangement_2::Halfedge_handle e)
{
return (edge_length (e));
}
/* The folowing is a workaround for a bug in the BGL upto and including version
* 103400.
*
* Unfortunately some of the calls to the get() function below from the BGL
* code are qualified with the boost namespace, while others are not. For The
* qualified calls the compiler naturally looks for the definition of the
* function in boost namespace. For the other calls it searches the CGAL
* namespace according to ADL (Koenig Lookup), as the type of the 1st
* parameter is in CGAL namespace.
*
* One way to get around it is to provide 2 similar functions that do the
* same thing. One in CGAL namespace provided in CGAL/Arr_vertex_map.h, and
* the other in boost namespace below. The signature of the latter is slightly
* changed to avoid redefinition. The type of its 1st parameter is defined in
* boost namespace, and is a simple derivation of the 1st parameter of the
* CGAL::get() function.
*/
namespace boost {
template <typename Arrangement_2>
class Arr_vertex_index_map_boost :
public CGAL::Arr_vertex_index_map<Arrangement_2>
{
public:
typedef CGAL::Arr_vertex_index_map<Arrangement_2> Base;
/*! Default constructor. */
Arr_vertex_index_map_boost() : Base() {}
/*! Constructor from CGAL index map. */
Arr_vertex_index_map_boost(Base & other) :
CGAL::Arr_vertex_index_map<Arrangement_2>(other)
{}
};
/*!
* Get the index property-map function. Provided so that boost is able to
* access the Arr_vertex_index_map above.
* \param index_map The index map.
* \param v A vertex handle.
* \return The vertex index.
*/
template<class Arrangement>
unsigned int
get(const boost::Arr_vertex_index_map_boost<Arrangement> & index_map,
typename Arrangement::Vertex_handle v)
{
const CGAL::Arr_vertex_index_map<Arrangement> & index_map_tmp =
static_cast<const CGAL::Arr_vertex_index_map<Arrangement> &>(index_map);
return CGAL::get<Arrangement>(index_map_tmp, v);
}
}
int main ()
{
Arrangement_2 arr;
// Construct an arrangement of seven intersecting line segments.
// We keep a handle for the vertex v_0 that corresponds to the point (1,1).
Arrangement_2::Halfedge_handle e =
insert_non_intersecting_curve (arr, Segment_2 (Point_2 (1, 1),
Point_2 (7, 1)));
Arrangement_2::Vertex_handle v0 = e->source();
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (3, 7)));
insert (arr, Segment_2 (Point_2 (1, 4), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (4, 4)));
insert (arr, Segment_2 (Point_2 (7, 1), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (3, 7), Point_2 (9, 3)));
// Create a mapping of the arrangement vertices to indices.
CGAL::Arr_vertex_index_map<Arrangement_2> index_map_tmp(arr);
boost::Arr_vertex_index_map_boost<Arrangement_2> index_map(index_map_tmp);
// Perform Dijkstra's algorithm from the vertex v0.
Edge_length_func edge_length;
CGAL::Arr_vertex_property_map<Arrangement_2,
double> dist_map (index_map);
boost::dijkstra_shortest_paths (arr, v0,
boost::vertex_index_map (index_map).
weight_map (edge_length).
distance_map (dist_map));
// Print the results:
Arrangement_2::Vertex_iterator vit;
std::cout << "The distances of the arrangement vertices from ("
<< v0->point() << ") :" << std::endl;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit)
{
std::cout << "(" << vit->point() << ") at distance "
<< dist_map[vit] << std::endl;
}
return (0);
}
60.6.2 Example for the Dual of an Arrangement as Graph
It is possible to give a dual graph representation for an arrangement instance, such that each arrangement face corresponds to a graph vertex and two vertices are adjacent iff the corresponding faces share a common edge on their boundaries. This is done by specializing the boost:graph_traits template for Dual<Arrangement_2> instances, where Dual<Arrangement_2> is a template specialization that gives a dual interpretation to an arrangement instance.
In dual representation, Arrangement_2::Face_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. We treat the graph edges as directed, such that a halfedge e is directed from , which is its incident face, to , which is the incident face of its twin halfedge. As two arrangement faces may share more than a single edge on their boundary, we allow parallel edges in our boost graph. As is the case in the primal graph, the dual arrangement graph is also a model of the concepts VertexListGraph, EdgeListGraph and BidirectionalGraph (thus also of IncidenceGraph).
Since we use Face_handle objects as the vertex descriptors, we define the Arr_face_index_map<Arrangement> class-template, which maintains an efficient mapping of face handles to indices. We also provide the template Arr_face_property_map<Arrangement,Type> for associating arbitrary data with the arrangement faces.
In the following example we construct the same arrangement as in example ex_bgl_primal_adapter.cpp (see Figure 60.1), and perform breadth-first search on the graph faces, starting from the unbounded face. We extend the DCEL faces with an unsigned integer, marking the discover time of the face and use a breadth-first-search visitor to obtain these times and update the faces accordingly:
File: examples/BGL_arrangement_2/dual.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arrangement_2.h>
#include <climits>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <CGAL/graph_traits_Dual_Arrangement_2.h>
#include <CGAL/Arr_face_map.h>
#include "arr_print.h"
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2,
unsigned int> Dcel;
typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2;
typedef CGAL::Dual<Arrangement_2> Dual_arrangement_2;
// A BFS visitor class that associates each vertex with its discover time.
// In our case graph vertices represent arrangement faces.
template <class IndexMap>
class Discover_time_bfs_visitor : public boost::default_bfs_visitor
{
private:
const IndexMap *index_map; // Mapping vertices to indices.
unsigned int time; // The current time stamp.
public:
// Constructor.
Discover_time_bfs_visitor (const IndexMap& imap) :
index_map (&imap),
time (0)
{}
// Write the discover time for a given vertex.
template <typename Vertex, typename Graph>
void discover_vertex (Vertex u, const Graph& )
{
u->set_data (time);
time++;
}
};
int main ()
{
Arrangement_2 arr;
// Construct an arrangement of seven intersecting line segments.
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (3, 7)));
insert (arr, Segment_2 (Point_2 (1, 4), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (4, 4)));
insert (arr, Segment_2 (Point_2 (7, 1), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (3, 7), Point_2 (9, 3)));
// Create a mapping of the arrangement faces to indices.
CGAL::Arr_face_index_map<Arrangement_2> index_map (arr);
// Perform breadth-first search from the unbounded face, and use the BFS
// visitor to associate each arrangement face with its discover time.
Discover_time_bfs_visitor<CGAL::Arr_face_index_map<Arrangement_2> >
bfs_visitor (index_map);
Arrangement_2::Face_handle uf = arr.unbounded_face();
boost::breadth_first_search (Dual_arrangement_2 (arr), uf,
boost::vertex_index_map (index_map).
visitor (bfs_visitor));
// Print the results:
Arrangement_2::Face_iterator fit;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit)
{
std::cout << "Discover time " << fit->data() << " for ";
if (fit != uf)
{
std::cout << "face ";
print_ccb<Arrangement_2> (fit->outer_ccb());
}
else
std::cout << "the unbounded face." << std::endl;
}
return (0);
}
Navigation: Up, Table of Contents, Package Overview, Bibliography, Index, Title Page , Acknowledging CGAL