|
CGAL 6.1 - 2D Straight Skeleton and Polygon Offsetting
|
|
CGAL 6.1 - 2D Straight Skeleton and Polygon Offsetting
|
This package implements weighted straight skeletons for two-dimensional polygons with holes. An intuitive way to think of the construction of straight skeletons is to imagine that wavefronts (or grassfires) are spawned at each edge of the polygon, and are moving inward. As the fronts progress, they either contract or expand depending on the angles formed between polygon edges, and sometimes disappear. Under this transformation, polygon vertices move along the angular bisector of the lines subtending the edges, tracing a tree-like structure, the straight skeleton.

Figure 21.2 Construction of a straight skeleton: the wavefront interfaces define the straight skeleton.
The straight skeleton of a polygon is similar to the medial axis and the Voronoi diagram of a polygon in the way it partitions it; however, unlike the medial axis and the Voronoi diagram, the bisectors are not equidistant to its defining edges but to the supporting lines of such edges. As a result, the bisectors of a straight skeleton might not be located in the center of the polygon and thus cannot be regarded as a proper medial axis in its geometrical meaning.
On the other hand, only reflex vertices (i.e., vertices whose internal angle \( > \pi\)) are responsible for deviations of the bisectors from its center location. Therefore, for convex polygons, the straight skeleton, the medial axis and the Voronoi diagram are exactly equivalent. Furthermore, if a non-convex polygon contains only vertices of low reflexivity, the straight skeleton bisectors will be placed nearly equidistant to their defining edges, producing a straight skeleton much alike a "proper" medial axis.
This package implements construction of straight skeletons as well as two typical use cases of the straight skeleton: polygon offsetting and straight skeleton extrusion.
We now define in detail what is the straight skeleton, starting from the input polygon.
A 2D contour is a closed sequence (a cycle) of three or more connected 2D oriented straight line segments called contour edges. The endpoints of contour edges are called vertices, and are shared by exactly two incident edges.
A contour partitions the plane in open regions that are bounded and unbounded. If the contour forms the boundary of a single open region that is a simply connected set, then this contour is said to be weakly simple. If the edges of the contour intersect only at their common vertices, the contour is said to be simple.
The orientation of a contour is given by the order of the vertices around the region they bound. It can be clockwise (CW) or counterclockwise (CCW). The bounded side of a contour edge is the side facing the bounded region of the contour. If the contour is oriented CCW, the bounded side of an edge is its left side.
A 2D polygon is a contour.
A 2D polygon with holes is a contour having zero or more contours in its bounded regions. The former contour is called outer contour or outer boundary, and the latter contours are called inner contours, or holes. In this chapter, we require that there cannot be any intersection among any two contours. Furthermore, we require that the outer contour is CCW oriented, that holes are CW oriented, and that a hole cannot be in the bounded region of another hole.
The intersection of the bounded regions of the outer contour and the unbounded regions of each inner contour is the interior of the polygon with holes. A polygon with holes is said to be weakly simple if its interior is a simply connected set.
Throughout the rest of this chapter the term polygon will be used as a shortcut for polygon with holes.
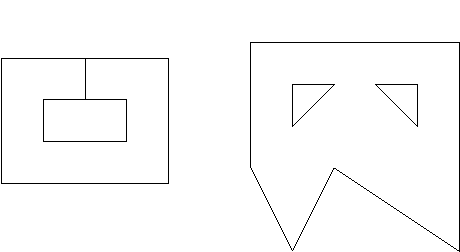
Figure 21.3 Examples of weakly simple polygons: one with no holes and two edges coincident (left) and one with 2 holes (right).
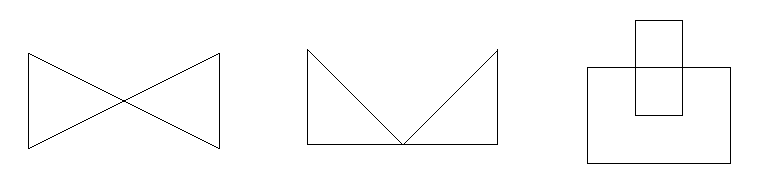
Figure 21.4 Examples of non-simple polygons: one folding into itself, that is, non-planar (left), one with a vertex touching an edge (middle), and one with a hole crossing into the outside (right)
Given a contour edge called the source edge, its offset edge at time t is an edge parallel with the same orientation such that the Euclidean distance between the lines supporting both edges is exactly t. An offset edge is always located to the bounded side of its source edge (which is an oriented straight line segment).
The straight skeleton is spawned by applying a continuous, inward offsetting to the contour edges. Under this transformation, polygon vertices move along the angular bisector of the lines subtending the edges, at a speed that depends on the angle between the two incident contour edges. So-called events happen when two moving vertices impact each other, or when a moving vertex collides with an offset edge. The different event types are detailed in the documentation of the class CGAL::Straight_skeleton_builder_2.
The straight skeleton is the set of segments traced out by the moving vertices during this process. It forms a unique partitioning of the polygon interior into straight skeleton regions corresponding to the monotone areas traced by the continuous inward offsetting of the contour edges. Each region corresponds to exactly 1 contour edge. These regions are bounded by the angular bisectors of the supporting lines of the contour edges, and each such region is itself a non-convex, weakly simple polygon.
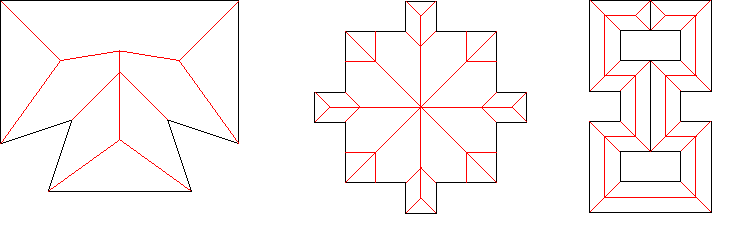
Figure 21.5 Straight skeletons of various weakly simple polygons.
The main entry points for straight skeletons are the following functions:
Weighted straight skeletons are a generalization of straight skeletons: contour edges are assigned a positive weight, which can be understood as assigning a speed to the wavefront spawned from the contour edge. Vertices no longer move along the angular bisector between two contour edges, but along a weighted bisector.
This CGAL package supports positive multiplicative weights: if the supporting line of a contour edge is described through the equation ax+by+c=0 then the supporting line of the offset edge at distance t is ax+by+c-t=0. With a multiplicative weight w, the equation becomes w(ax+by+c)-t=0. Therefore, a larger weight implies a faster moving front.
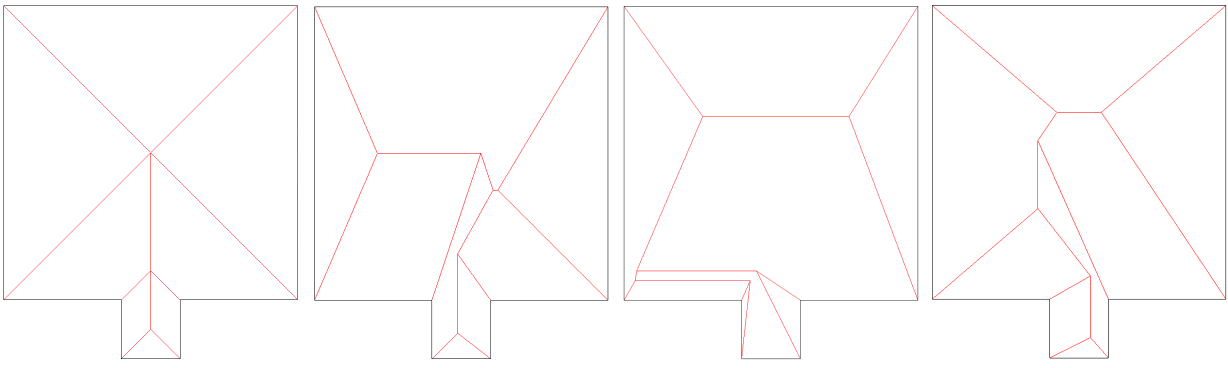
Figure 21.6 An unweighted straight skeleton (leftmost) and three randomly weighted straight skeletons.
A significant change from unweighted straight skeleton of polygon with holes is that the faces of a straight skeleton of a polygon with holes are no longer necessarily weakly simple polygons: a face can for example completely encompass a set of faces incident to a hole, giving it the topology of a ring. This property is essential, both to have a valid halfedge data structure (e.g., one cannot have a face with multiple boundaries), and to correctly extract the offset contours of the straight skeleton. Thus, a post processing step is applied to ensure the weakly simple property in all faces. This post processing adds so-called artificial bisector/vertices where required to cut the face into a weakly simple polygon. This is achieved by shooting a ray from the farthest (w.r.t. time) vertex for each boundary that does not contain the defining contour edge of its incident face.

Figure 21.7 A polygon with four holes (black) and its straight skeleton (red). Three artificial bisectors (green) are added in a postprocessing step to recover the simply-connected property for the straight skeleton face (gray) of the rightmost vertical contour edge.
The main entry points for weighted straight skeletons are the following functions:
A straight skeleton can also be defined for a general multiply-connected, planar, directed straight-line graph by considering all the edges as embedded in an unbounded region [1]. The only difference is that in this case some faces will be only partially bounded.
The current version of this CGAL package can only construct the straight skeleton in the interior of a simple polygon with holes, that is it does not handle general polygonal figures in the plane.
The straight skeleton is defined by the trace of the moving vertices, but one can also consider the state of the polygon at a fixed time t made up of the translated vertices. This is the offset polygon.
An offset polygon can have fewer, equal, or more sides as its source polygon. It can even be composed of multiple polygons. If the source polygon has no holes, then no offset polygon has any holes. If the source polygon has holes, any of the offset polygons can have holes itself, but it might as well have no holes at all (if the distance is sufficiently large). Each offset polygon has the same orientation as the source polygon.
The main entry points for polygon offsetting are the following functions:
This CGAL package can only construct the straight skeleton and offset contours in the interior of a polygon with holes. However, constructing exterior skeletons and exterior offsets is possible.
Say you have some polygon with one hole, and you wish to obtain some exterior offset contours. The interior region of a polygon with holes is connected while the exterior region is not: there is an unbounded region outside the outer contour, and one bounded region inside each hole. To construct an offset contour you need to construct a straight skeleton. Thus, to construct exterior offset contours for a polygon with holes, you need to construct, separately, the exterior skeleton of the outer contour and the interior skeleton of each hole.
Constructing the interior skeleton of a hole is directly supported by this CGAL package; you simply need to input the hole's vertices in reversed order as if it were an outer contour as to treat them as simple polygons without holes. The offset contour(s) should also be reversed.
Constructing the exterior skeleton of the outer contour is achieved by means of the following trick: consider the outer contour as a hole of a larger rectangle (call it frame). If the frame is sufficiently separated from the contour, the resulting skeleton will be equivalent to a real exterior skeleton once the offset contour corresponding to the outer frame is removed, which is performed automatically by some of the functions of this package.

Figure 21.8 Exterior skeleton obtained using a frame (left) and 2 sample exterior offset contours (right)
It is necessary to place the frame sufficiently far away from the contour. If it is not, it could occur that the outward offset contour collides and merges with the inward offset frame, resulting in 1 instead of 2 offset contours. However, the proper separation between the contour and the frame is not directly given by the offset distance at which you want the offset contour. That distance must be at least the desired offset plus the largest Euclidean distance between an offset vertex and its original. This CGAL packages provides a helper function to compute the required separation: compute_outer_frame_margin().
For convenience, the following functions are provided:
CGAL::create_exterior_skeleton_and_offset_polygons_2(), which adds the outer frame to the input polygon (with or without holes) and provides output offset polygons (CGAL::Polygon_2), including the offset of the outer frame. CGAL::create_exterior_skeleton_and_offset_polygons_with_holes_2(), which adds the outer frame to the input polygon (with or without holes) and provides as output offset polygons with holes (CGAL::Polygon_with_holes_2), excluding the offset of the outer frame. These also exists in weighted versions.
Perhaps the first (historically) use-case of straight skeletons: given a polygonal roof, the straight skeleton directly gives the layout of each tent. If each skeleton edge is lifted from the plane a height equal to its offset distance, the resulting roof is "correct" in that water will always fall down to the contour edges (the roof's border), regardless of where it falls on the roof. Laycock and Day [4] give an algorithm for roof design based on the straight skeleton.
This CGAL package implements skeleton extrusion for polygons with holes, with support for positive multiplicative weights. The output is a closed, combinatorially 2-manifold surface triangle mesh.
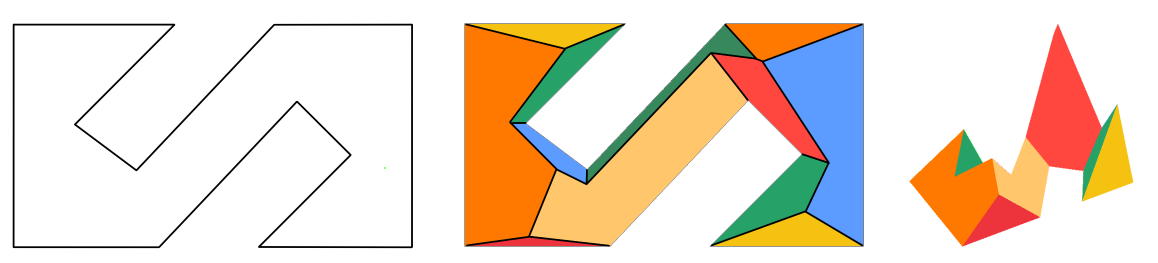
Figure 21.9 Input polygon (left), weighted skeleton with colored faces (middle), and extruded skeleton (right).
The main entry point for straight skeleton extrusion is the function CGAL::extrude_skeleton(), whose API also enables passing angles for each tent, which are then converted internally to edge weights.
The extrusion can be performed to a maximum height, as shown in the figure below.

Figure 21.10 Input polygon with three holes and its weighted straight skeleton (left), and two extrusions of the skeleton with different maximum heights (middle and right).
Just like medial axes, straight skeletons can also be used for 2D shape description and matching. Essentially, all the applications of image-based skeletonization (for which there is a vast literature) are also direct applications of the straight skeleton, especially since skeleton edges are simply straight line segments.
Consider the subgraph formed only by inner bisectors (that is, only the skeleton edges which are not incident upon a contour vertex). Call this subgraph a skeleton axis. Each node in the skeleton axis whose degree is \( >=3\) roots more than one skeleton tree. Each skeleton tree roughly corresponds to a region in the input topologically equivalent to a rectangle; that is, without branches. For example, a simple character "H" would contain 2 higher degree nodes separating the skeleton axis in 5 trees; while the character "@" would contain just 1 higher degree node separating the skeleton axis in 2 curly trees.
Since a skeleton edge is a straight line, each branch in a skeleton tree is a polyline. Thus, the path-length of the tree can be directly computed. Furthermore, the polyline for a particular tree can be interpolated to obtain curve-related information.
Pruning each skeleton tree cutting off branches whose length is below some threshold; or smoothing a given branch, can be used to reconstruct the polygon without undesired details, or fit into a particular canonical shape.
Each skeleton edge in a skeleton branch is associated with 2 contour edges which are facing each other. If the polygon has a bottleneck (it almost touches itself), a search in the skeleton graph measuring the distance between each pair of contour edges will reveal the location of the bottleneck, allowing you to cut the shape in two. Likewise, if two shapes are too close to each other along some part of their boundaries (a near contact zone), a similar search in an exterior skeleton of the two shapes at once would reveal the parts of near contact, allowing you to stitch the shapes. These cut and stitch operations can be directly executed in the straight skeleton itself instead of the input polygon (because the straight skeleton contains a graph of the connected contour edges).
The reference manual of this CGAL package contains many details about the straight skeleton construction algorithm that has been implemented. In particular, the classes and CGAL::Straight_skeleton_2 and CGAL::Straight_skeleton_builder_2 describe the algorithm in depth.
The straight skeleton data structure is implemented in the class CGAL::Straight_skeleton_2.
The simplest way to construct a straight skeleton is via the free functions CGAL::create_interior_straight_skeleton_2() and CGAL::create_exterior_straight_skeleton_2(), as shown in the following example:
File Straight_skeleton_2/Create_straight_skeleton_2.cpp
The input to these functions is the polygon, which can be given as an iterator pair or directly as a CGAL::Polygon_2 object. In the case of the exterior skeleton, a maximum offset must be specified as well (see Section Straight_skeleton_2ExteriorSkeletonsandExterior for details on this max offset parameter).
If CGAL::Polygon_with_holes_2 is used, you can pass an instance of it directly to the function creating the interior skeleton, as shown below. Notice that a different header must be included in this case.
File Straight_skeleton_2/Create_straight_skeleton_from_polygon_with_holes_2.cpp
If you already have a straight skeleton object, the simpler way to generate offset polygons is to call CGAL::create_offset_polygons_2() as shown in the next example, passing the desired offset and the straight skeleton. You can reuse the same skeleton to generate offsets at a different distance, which is recommended because producing the straight skeleton is much slower than generating offset polygons.
File Straight_skeleton_2/Create_offset_polygons_2.cpp
If you need offset polygons at a single distance, you can hide away the construction of the straight skeleton by calling directly the functions CGAL::create_interior_skeleton_and_offset_polygons_2() and CGAL::create_exterior_skeleton_and_offset_polygons_2() as shown in the following examples:
File Straight_skeleton_2/Create_skeleton_and_offset_polygons_2.cpp
... and using a Polygon_with_holes_2 directly when available:
File Straight_skeleton_2/Create_saop_from_polygon_with_holes_2.cpp
If the input polygon has holes, there can be holes in the offset polygons. However, the polygons generated by all the offsetting functions shown before do not have any parent-hole relationship computed; that is, they just instances of Polygon_2 instead of Polygon_with_holes_2. If Polygon_with_holes_2 are available and you need the offsetting to produce them, you can call the function CGAL::arrange_offset_polygons_2() passing the result of any of the offsetting functions described so far. That function arranges the offset polygons detecting and distributing holes within parents. As a shortcut, you can use the function CGAL::create_interior_skeleton_and_offset_polygons_with_holes_2() as shown below:
File Straight_skeleton_2/Create_skeleton_and_offset_polygons_with_holes_2.cpp
Consider an input polygon with parallel edges separated a distance \( 2*t\). If you produce an offset polygon at distance \( t\), these parallel edges will just collapse each other and vanish from the result, keeping the output as a simple polygon, just like the input. However, if you request an offset polygon at a distance \( t-epsilon\), the result will still be a simple polygon but with edges that are so close to each other that will almost intersect. If a kernel with exact constructions is used, the offsetting algorithm can guarantee that the output contains only simple polygons. However, if inexact constructions are used the roundoff in the coordinates of the output points will cause parallel edges that almost collapse-but not so-to become really collinear or even cross each other.
Thus, it is necessary to use a kernel with exact constructions if offset polygons must be simple, yet computing a straight skeleton using that kernel is very slow, much more than computing the offset polygons. To help with this, it is possible to construct the straight skeleton using the recommended kernel Exact_predicates_inexact_constructions_kernel, then convert the skeleton to a different kernel via the function CGAL::convert_straight_skeleton_2() and input the converted skeleton to the offsetting functions.
All the offsetting functions that take polygons as input (and create the straight skeleton under the hood) apply that optimization automatically: that is, the output polygons are defined over the same kernel of the input polygons, whatever that is, yet the straight skeleton is constructed with the faster recommended kernel and converted if necessary.
Notice how some of the examples above use Exact_predicates_exact_constructions_kernel. In all cases, the straight skeleton is constructed using Exact_predicates_inexact_constructions_kernel.
The following example shows how to extrude the weighted skeleton of a polygon with holes:
File Straight_skeleton_2/extrude_skeleton.cpp
All the high level functions described above are just wrappers around the low-level API described here. This low level API is richer and provides options and configurations not covered by any of those functions.
The straight skeleton construction algorithm is encapsulated in the class CGAL::Straight_skeleton_builder_2, which is parameterized by a geometric traits (CGAL::Straight_skeleton_builder_traits_2) and the Straight Skeleton class.
The offset contours construction algorithm is encapsulated in the class CGAL::Polygon_offset_builder_2, which is parameterized by the Straight Skeleton class, a geometric traits (Polygon_offset_builder_traits_2<Kernel>) and a container type where the resulting offset polygons are generated.
To construct the straight skeleton of a polygon the user must:
Straight_skeleton_builder_2::enter_contour(). The input polygon must be weakly simple and counterclockwise oriented (see the definitions at the beginning of this chapter). Collinear edges are allowed. The insertion order of each hole is unimportant but the outer contour must be entered first. Straight_skeleton_builder_2::construct_skeleton() once all the contours have been entered. You cannot enter another contour once the skeleton has been constructed. To construct a set of inward offset contours the user must:
Polygon_offset_builder_2::construct_offset_contours() passing the desired offset distance and an output iterator that can store a std::shared_ptr of Container instances into a resulting sequence (typically, a back insertion iterator) Each element in the resulting sequence is an offset contour, given by a std::shared_ptr holding a dynamically allocated instance of the Container type. Such a container can be any model of the SequenceContainer concept, for example, a CGAL::Polygon_2, or just a std::vector of 2D points.
The resulting sequence of offset contours can contain both outer and inner contours. Each offset hole (inner offset contour) would logically belong in the interior of some of the outer offset contours. However, this algorithm returns a sequence of contours in arbitrary order and there is no indication whatsoever of the parental relationship between inner and outer contours.
On the other hand, each outer contour is counterclockwise oriented while each hole is clockwise-oriented. And since offset contours do form simple polygons, it is guaranteed that no hole will be inside another hole, no outer contour will be inside any other contour, and each hole will be inside exactly 1 outer contour.
Parental relationships are not automatically reconstructed by this algorithm because this relation is not directly given by the input polygon and must be done as a postprocessing step. The function CGAL::arrange_offset_polygons_2() can be used to do that efficiently.
A user can reconstruct the parental relationships as a post processing operation by testing each inner contour (which is identified by being clockwise) against each outer contour (identified as being counterclockwise) for insideness.
This algorithm requires exact predicates but not exact constructions. Therefore, the Exact_predicates_inexact_constructions_kernel should be used.
File Straight_skeleton_2/Low_level_API.cpp
Fernando Cacciola created the first version of this package, providing unweighted straight skeletons and polygon offsetting.
Sébastien Loriot and Mael Rouxel-Labbé implemented further robustification techniques, as well as weighted straight skeletons, and skeleton extrusion.