|
CGAL 6.1 - 2D Straight Skeleton and Polygon Offsetting
|
|
CGAL 6.1 - 2D Straight Skeleton and Polygon Offsetting
|
#include <CGAL/Straight_skeleton_2.h>
CGAL::HalfedgeDS_default< Traits >.
The class Straight_skeleton_2 provides a model for the StraightSkeleton_2 concept which is the class type used to represent a straight skeleton.
StraightSkeleton_2 | Traits | must be a model of Kernel |
The only purpose of this class is to protect all the modifying operations in a HalfedgeDS. Normal users should not modify a straight skeleton. If an advanced user needs to get access to the modifying operations, it must call the required methods through the Base class.
Below is an in-depth description of the combinatorial representation used in the straight skeleton class, starting with a few definitions describing the different concepts appearing in the algorithm.
Angular Bisecting Lines and Offset Bisectors
We make use of definitions from the user manual, see Section Definitions.
Given two points and a line passing through them, the perpendicular line passing through the midpoint is the bisecting line (or bisector) of those points. Two non-parallel lines, intersecting at a point, are bisected by two other lines passing through that intersection point. Two parallel lines are bisected by another parallel line placed halfway in between. Given just one line, any perpendicular line can be considered the bisecting line (any bisector of any two points along the single line). The bisecting lines of two edges are the lines bisecting the supporting lines of the edges (if the edges are parallel or collinear, there is just one bisecting line).
The halfplane to the bounded side of the line supporting a contour (input) edge is called the offset zone of the contour edge. Given any number of contour edges (not necessarily consecutive), the intersection of their offset zones is called their combined offset zone.
Any two contour edges define an offset bisector, as follows: If the edges are non-parallel, their bisecting lines can be decomposed as 4 rays originating at the intersection of the supporting lines. Only one of these rays is contained in the combined offset zone of the edges (which one depends on the possible combinations of orientations). This ray is the offset bisector of the non-parallel contour edges.
If the edges are parallel (but not collinear) and have opposite orientation, the entire and unique bisecting line is their offset bisector. If the edges are parallel but have the same orientation, there is no offset bisector between them.
If the edges are collinear and have the same orientation, their offset bisector is given by a perpendicular ray to the left of the edges which originates at the midpoint of the combined complement of the edges. (The complement of an edge/segment are the two rays along its supporting line which are not the segment and the combined complement of N collinear segments is the intersection of the complements of each segment). If the edges are collinear but have opposite orientation, there is no offset bisector between them.
Faces, Edges, and Vertices
Each region of the partitioning defined by a straight skeleton is called a face. Each face is bounded by straight line segments, called edges. Exactly one edge per face is a contour edge (corresponds to a side of the polygon) and the rest of the edges, located in the interior of the polygon, are called skeleton edges, or bisectors.
The bisectors of the straight skeleton are segments of the offset bisectors as defined previously. Since an offset bisector is a ray of a bisecting line of 2 contour edges, each skeleton edge (or bisector) is uniquely given by two contour edges. These edges are called the defining contour edges of the bisector.
The intersection of the edges are called vertices. Although in a simple polygon, only 2 edges intersect at a vertex, in a straight skeleton, 3 or more edges intersect at any given vertex. That is, vertices in a straight skeleton have degree \( >=3\).
A contour vertex is a vertex for which 2 of its incident edges are contour edges.
A skeleton vertex is a vertex whose incident edges are all skeleton edges.
A contour bisector is a bisector whose defining contour edges are consecutive. Such a bisector is incident upon 1 contour vertex and 1 skeleton vertex, and touches the input polygon at exactly 1 endpoint.
An inner bisector is a bisector whose defining contour edges are not consecutive. Such a bisector is incident upon 2 skeleton vertices and is strictly contained in the interior of the polygon.
Implementation Details
This CGAL package represents a straight skeleton as a specialized CGAL::HalfedgeDS (HDS) whose vertices embed 2D Points (see the StraightSkeleton_2 concept in the reference manual for details).
Its halfedges, by considering the source and target points, implicitly embed 2D oriented straight line segments (each halfedge per se does not embed a segment explicitly).
A face of the straight skeleton is represented as a face in the HDS. Both contour and skeleton edges are represented by pairs of opposite HDS halfedges, and both contour and skeleton vertices are represented by HDS vertices.
In a HDS, a border halfedge is a halfedge which does not have an incident face. In the case of the straight skeleton HDS, such border halfedges are oriented such that their left side faces outwards the polygon. Therefore, the opposite halfedge of any border halfedge is oriented such that its left side faces inward the polygon.
This CGAL package requires the input polygon (with holes) to be weakly simple and oriented counterclockwise.
The skeleton halfedges are oriented such that their left side faces inward the region they bound. That is, the vertices (both contour and skeleton) of a face are circulated in counterclockwise order. There is one and only one contour halfedge incident upon any face.
The contours of the input polygon are traced by the border halfedges of the HDS (those facing outward), but in the opposite direction. That is, the vertices of the contours can only be traced from the straight skeleton data structure by circulating the border halfedges, and the resulting vertex sequence will be reversed w.r.t. the input vertex sequence.
A skeleton edge, according to the definition given in the previous section, is defined by 2 contour edges. In the representation, each one of the opposite halfedges that represent a skeleton edge is associated with one of the opposite halfedges that correspond to one of its defining contour edges. Thus, the 2 opposite halfedges of a skeleton edge link the edge to its 2 defining contour edges.
Starting from any border contour halfedge, circulating the structure walks through border counter halfedges and traces the vertices of the polygon's contours (in opposite order).
Starting from any non-border but contour halfedge, circulating the structure walks counterclockwise around the face corresponding to that contour halfedge. The vertices around a face always describe a non-convex weakly simple polygon.
A vertex is the intersection of contour and/or skeleton edges. Since a skeleton edge is defined by 2 contour edges, any vertex is itself defined by a unique set of contour edges. These are called the defining contour edges of the vertex.
A vertex is identified by its set of defining contour edges. Two vertices are distinct if they have differing sets of defining contour edges. Note that vertices can be distinct even if they are geometrically embedded at the same point.
The degree of a vertex is the number of halfedges around the vertex incident upon (pointing to) the vertex. As with any halfedge data structure, there is one outgoing halfedge for each incoming (incident) halfedge around a vertex. The degree of the vertex counts only incoming (incident) halfedges.
In a straight skeleton, the degree of a vertex is not only the number of incident halfedges around the vertex but also the number of defining contour halfedges. The vertex itself is the point where all the defining contour edges simultaneously collide.
Contour vertices have exactly two defining contour halfedges, which are the contour edges incident upon the vertex; and 3 incident halfedges. One and only one of the incident halfedges is a skeleton halfedge. The degree of a contour vertex is exactly 3.
Skeleton vertices have at least 3 defining contour halfedges and 3 incident skeleton halfedges. If more than 3 edges collide simultaneously at the same point and time (like in any regular polygon with more than 3 sides), the corresponding skeleton vertex will have more than 3 defining contour halfedges and incident skeleton halfedges. That is, the degree of a skeleton vertex is \( >=3\) (the algorithm initially produces nodes of degree 3 but in the end all coincident nodes are merged to form higher degree nodes). All halfedges incident upon a skeleton vertex are skeleton halfedges.
The defining contour halfedges and incident halfedges around a vertex can be traced using the circulators provided by the vertex class. The degree of a vertex is not cached and cannot be directly obtained from the vertex, but you can calculate this number by manually counting the number of incident halfedges around the vertex.
Each vertex stores a 2D point and a time, which is the Euclidean distance from the vertex's point to the lines supporting each of the defining contour edges of the vertex (the distance is the same to each line). Unless the polygon is convex, this distance is not equal to the edges, as in the case of a Medial Axis, therefore, the time of a skeleton vertex does not correspond to the distance from the polygon to the vertex (so it cannot be used to obtain the deep of a region in a shape, for instance).
If the polygon is convex, the straight skeleton is exactly equivalent to the polygon's Voronoi diagram and each vertex time is the equidistance to the defining edges.
Contour vertices have time zero.
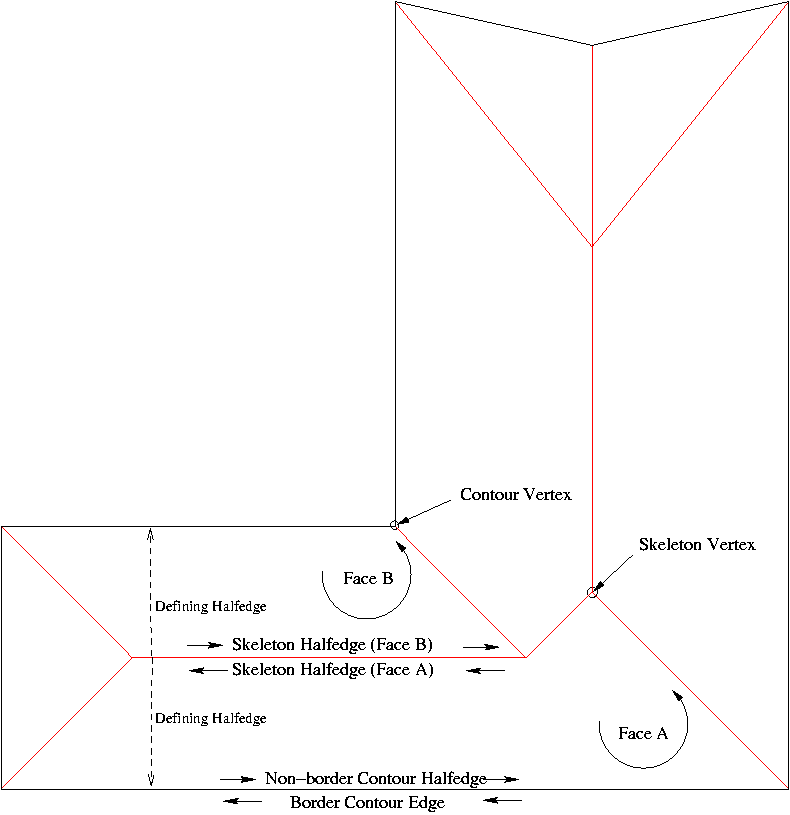
Figure 21.1 Straight Skeleton Data Structure
Public Types | |
| typedef unspecified_type | Base |
| Access to the base (HDS) class. | |