Authors: Michael Hemmer, Kan Huang, Francisc Bungiu, Ning Xu

Introduction

This package provides functionality to compute the visibility region within polygons in two dimensions. The package is based on the package 2D Arrangements and uses CGAL::Arrangement_2 as the fundamental class to specify the input as well as the output. Hence, a polygon $ P $ is represented by a bounded arrangement face $ f $ that does not have any isolated vertices and any edge that is adjacent to $ f $ separates $ f $ from another face. Note that $ f $ may contain holes. Similarly, a simple polygon is represented by a face without holes.

Given two points $ p $ and $ q $ in $ P $, they are said to be visible to each other iff the segment $ pq \subset P $, where $ P $ is considered to be closed, that is, $\partial P \subset P$. For a query point $ q \in P $, the set of points that are visible from $ q $ is defined as the visibility region of $ q $, denoted by $ V_q $

Degeneracies and Regularization

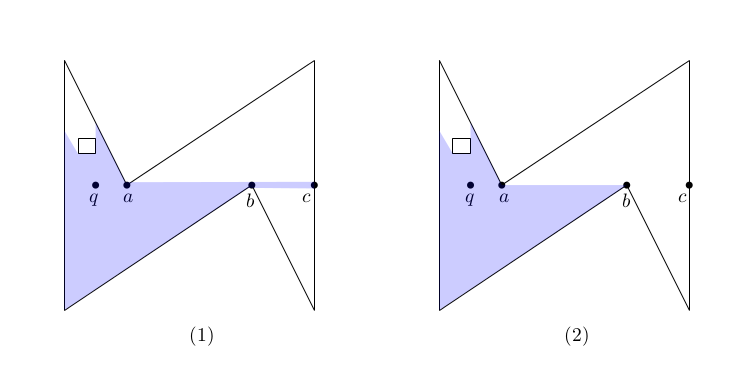
Figure 24.1 Non-regularized visibility and regularized visibility.

As illustrated in Figure 24.1 (1) the visibility region $ V_q $ of a query point $ q $ may not be a polygon. In the figure, all labeled points are collinear, which implies that the point $ c $ is visible to $ q $, that is, the segment $ bc $ is part of $ V_q $. We call such low dimensional features that are caused by degeneracies needles. However, for many applications these needles are actually irrelevant. Moreover, for some algorithms it is even more efficient to ignore needles in the first place. Therefore, this package offers also functionality to compute the regularized visibility area $ \overline{V_q} = closure(interior(V_q)) = (V_q\setminus\partial V_q) \cup \partial (V_q\setminus\partial V_q)$, as shown in Figure 24.1 (2). For more information about regularization, refer to Chapter 2D Regularized Boolean Set-Operations.

Classes and Algorithms

Answering visibility queries is, in many ways, similar to answering point-location queries. Thus, we use the same design used to implement 2D Arrangements point location. Each of the various visibility class templates employs a different algorithm or strategy for answering queriesThe term strategy is borrowed from the design-pattern taxonomy [3]. A strategy provides the means to define a family of algorithms, each implemented by a separate class. All classes that implement the various algorithms are made interchangeable, letting the algorithm in use vary according to the user choice.. Similar to the point-location case, some of the strategies require preprocessing. Thus, before a visibility object is used to answer visibility queries, it must be attached to an arrangement object. Afterwards, the visibility object observes changes to the attached arrangement. Hence, it is possible to modify the arrangement after attaching the visibility object. However, this feature should be used with caution as each change to the arrangement also requires an update of the auxiliary data structures in the attached object.

An actual query is performed by giving the view point $ p $ and its containing face $ f $ (which must represent a valid polygon) to a visibility object. For more details see the documentation of the overloaded member function Visibility_2::compute_visibility().

The following models of the Visibility_2 concept are provided:

Class	Function	Preprocessing	Query	Algorithm
`Simple_polygon_visibility_2`	simple polygons	No	$O(n)$$ time and $O(n)$$ space	B. Joe and R. B. Simpson [4]
`Rotational_sweep_visibility_2`	polygons with holes	No	$O(n\log n)$$ time and $O(n)$$ space	T. Asano [1]
`Triangular_expansion_visibility_2`	polygons with holes	$O(n)$$ time and $O(n)$$ space	$O(nh)$$ time and $O(n)$$ space.	Bungiu et al. [2]

Where $ n $ denotes the number of vertices of $ f $ and $ h $ the number of holes+1.

Running Time in Practice

Figure 24.2 Example representing a cathedral.

The left hand side of Figure Figure 24.2 depicts the outer boundary of a cathedral, which is a simple polygon with 565 vertices. The right hand side shows the cathedral also with its inner pillars, which is a polygon (with holes) with 1153 vertices. The following table shows the total running time consumption of the computation of all visibility polygons for all vertices of the cathedral.

Boundary Cathedral	total preprocessing time	total query time
`Simple_polygon_visibility_2`	-	0.38
`Rotational_sweep_visibility_2`	-	1.01
`Triangular_expansion_visibility_2`	0.01	0.06

The second table shows the same for the complete cathedral. The table does not report the time for Simple_polygon_visibility_2 as this algorithm can only handle simple polygons.

Complete Cathedral	total preprocessing time	total query time
`Rotational_sweep_visibility_2`	-	1.91
`Triangular_expansion_visibility_2`	0.01	0.04

Thus, in general we recommend to use Triangular_expansion_visibility_2 even if the polygon is simple. The main advantage of the algorithm is its locality. After the triangle that contains the query point is located in the triangulation, the algorithm explores neighboring triangles, but only those that are actually seen. In this sense the algorithm can be considered as output sensitive. Note that the Triangular_expansion_visibility_2 algorithm performs better on the full cathedral since the additional pillars block the view early in many cases. However, if the simple polygon is rather convex (i.e., nearly all boundary is seen) or if only one (or very little) queries are required, using one of the algorithms that does not require preprocessing is advantageous.

Example of Visibility in a Simple Polygon

The following example shows how to obtain the regularized and non-regularized visibility regions.

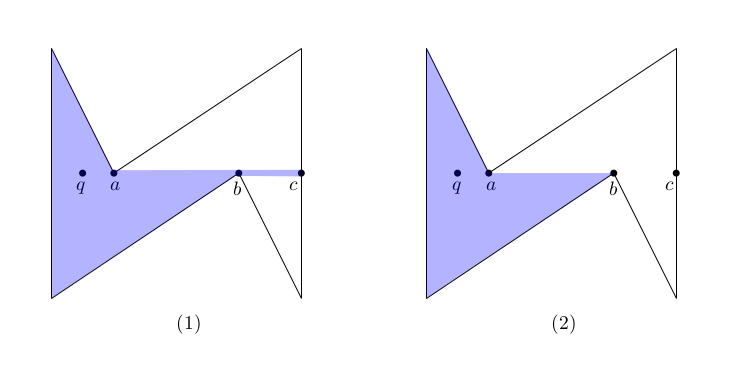
Figure 24.3 The visibility region of $ q $ in a simple polygon: (1) non-regularized visibility; and (2) regularized visibility.

File Visibility_2/simple_polygon_visibility_2.cpp

 
#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/Simple_polygon_visibility_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_naive_point_location.h>
#include <istream>
#include <vector>
 
typedef CGAL::Exact_predicates_exact_constructions_kernel               Kernel;
typedef Kernel::Point_2                                                 Point_2;
typedef Kernel::Segment_2                                               Segment_2;
typedef CGAL::Arr_segment_traits_2<Kernel>                              Traits_2;
typedef CGAL::Arrangement_2<Traits_2>                                   Arrangement_2;
typedef Arrangement_2::Face_handle                                      Face_handle;
typedef Arrangement_2::Edge_const_iterator                              Edge_const_iterator;
typedef Arrangement_2::Ccb_halfedge_circulator                          Ccb_halfedge_circulator;
 
 
int main() {
  //create environment
  Point_2 p1(0,4), p2(0,0), p3(3,2), p4(4,0), p5(4,4), p6(1,2);
  std::vector<Segment_2> segments;
  segments.push_back(Segment_2(p1, p2));
  segments.push_back(Segment_2(p2, p3));
  segments.push_back(Segment_2(p3, p4));
  segments.push_back(Segment_2(p4, p5));
  segments.push_back(Segment_2(p5, p6));
  segments.push_back(Segment_2(p6, p1));
 
  Arrangement_2 env;
  CGAL::insert_non_intersecting_curves(env,segments.begin(),segments.end());
 
  // find the face of the query point
  // (usually you may know that by other means)
  Point_2 q(0.5, 2);
  Arrangement_2::Face_const_handle * face;
  CGAL::Arr_naive_point_location<Arrangement_2> pl(env);
  CGAL::Arr_point_location_result<Arrangement_2>::Type obj = pl.locate(q);
  // The query point locates in the interior of a face
  face = std::get_if<Arrangement_2::Face_const_handle> (&obj);
 
  // compute non regularized visibility area
  // Define visibility object type that computes non-regularized visibility area
  typedef CGAL::Simple_polygon_visibility_2<Arrangement_2, CGAL::Tag_false> NSPV;
  Arrangement_2 non_regular_output;
  NSPV non_regular_visibility(env);
 
  non_regular_visibility.compute_visibility(q, *face, non_regular_output);
 
  std::cout << "Non-regularized visibility region of q has "
            << non_regular_output.number_of_edges()
            << " edges:" << std::endl;
  for (Edge_const_iterator eit = non_regular_output.edges_begin(); eit != non_regular_output.edges_end(); ++eit)
    std::cout << "[" << eit->source()->point() << " -> " << eit->target()->point() << "]" << std::endl;
 
 
  // compute non regularized visibility area
  // Define visibility object type that computes regularized visibility area
  typedef CGAL::Simple_polygon_visibility_2<Arrangement_2, CGAL::Tag_true> RSPV;
  Arrangement_2 regular_output;
  RSPV regular_visibility(env);
 
  regular_visibility.compute_visibility(q, *face, regular_output);
 
  std::cout << "Regularized visibility region of q has "
            << regular_output.number_of_edges()
            << " edges:" << std::endl;
  for (Edge_const_iterator eit = regular_output.edges_begin(); eit != regular_output.edges_end(); ++eit)
    std::cout << "[" << eit->source()->point() << " -> " << eit->target()->point() << "]" << std::endl;
 
  return 0;
}
 

Example of Visibility in a Polygon with Holes

The following example shows how to obtain the regularized visibility region using the model Triangular_expansion_visibility_2, see Figure 24.4. The arrangement has six bounded faces and an unbounded face. The query point $ q $ is on a vertex. The red arrow denotes the halfedge $ \overrightarrow{pq} $, which also identifies the face in which the visibility region is computed.

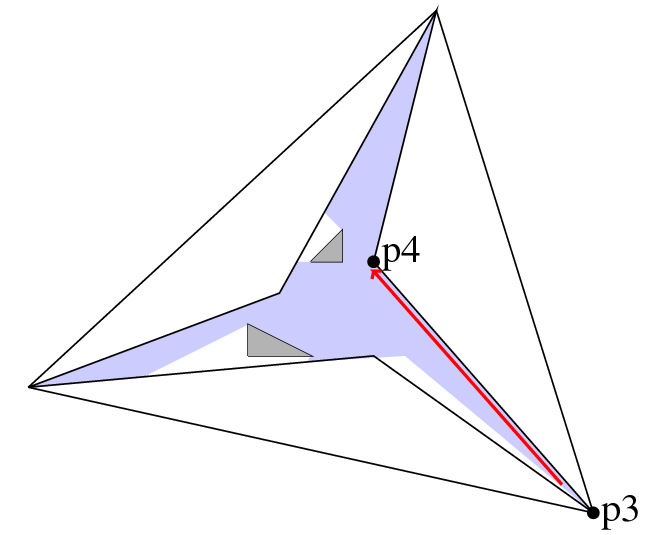
Figure 24.4 The visibility region of $ q $ in a polygon with two holes.

File Visibility_2/general_polygon_example.cpp

 
#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/Triangular_expansion_visibility_2.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <iostream>
#include <vector>
 
// Define the used kernel and arrangement
typedef CGAL::Exact_predicates_exact_constructions_kernel       Kernel;
typedef Kernel::Point_2                                         Point_2;
typedef Kernel::Segment_2                                       Segment_2;
typedef CGAL::Arr_segment_traits_2<Kernel>                      Traits_2;
typedef CGAL::Arrangement_2<Traits_2>                           Arrangement_2;
typedef Arrangement_2::Halfedge_const_handle                    Halfedge_const_handle;
typedef Arrangement_2::Face_handle                              Face_handle;
 
// Define the used visibility class
typedef CGAL::Triangular_expansion_visibility_2<Arrangement_2>  TEV;
 
int main() {
  // Defining the input geometry
  Point_2 p1(1,2), p2(12, 3), p3(19,-2), p4(12,6), p5(14,14), p6( 9,5);
  Point_2 h1(8,3), h2(10, 3), h3( 8, 4), h4(10,6), h5(11, 6), h6(11,7);
  std::vector<Segment_2> segments;
  segments.push_back(Segment_2(p1,p2));
  segments.push_back(Segment_2(p2,p3));
  segments.push_back(Segment_2(p3,p4));
  segments.push_back(Segment_2(p4,p5));
  segments.push_back(Segment_2(p5,p6));
  segments.push_back(Segment_2(p6,p1));
 
  segments.push_back(Segment_2(h1,h2));
  segments.push_back(Segment_2(h2,h3));
  segments.push_back(Segment_2(h3,h1));
  segments.push_back(Segment_2(h4,h5));
  segments.push_back(Segment_2(h5,h6));
  segments.push_back(Segment_2(h6,h4));
 
  // insert geometry into the arrangement
  Arrangement_2 env;
  CGAL::insert_non_intersecting_curves(env,segments.begin(),segments.end());
 
  //Find the halfedge whose target is the query point.
  //(usually you may know that already by other means)
  Point_2 query_point = p4;
  Halfedge_const_handle he = env.halfedges_begin();
  while (he->source()->point() != p3 || he->target()->point() != p4)
    he++;
 
  //visibility query
  Arrangement_2 output_arr;
  TEV tev(env);
  Face_handle fh = tev.compute_visibility(query_point, he, output_arr);
 
  //print out the visibility region.
  std::cout << "Regularized visibility region of q has "
            << output_arr.number_of_edges()
            << " edges." << std::endl;
 
  std::cout << "Boundary edges of the visibility region:" << std::endl;
  Arrangement_2::Ccb_halfedge_circulator curr = fh->outer_ccb();
  std::cout << "[" << curr->source()->point() << " -> " << curr->target()->point() << "]" << std::endl;
  while (++curr != fh->outer_ccb())
    std::cout << "[" << curr->source()->point() << " -> " << curr->target()->point() << "]"<< std::endl;
  return 0;
}

Implementation History

This package was first developed during Google Summer of Code 2013: Francisc Bungiu developed the CGAL::Simple_polygon_visibility_2, Kan Huang developed the CGAL::Rotational_sweep_visibility_2, and Michael Hemmer developed the CGAL::Triangular_expansion_visibility_2.

During Google Summer of Code 2014 Ning Xu fixed a bug in CGAL::Simple_polygon_visibility_2 and improved the testsuite.

Class	Function	Preprocessing	Query	Algorithm
`Simple_polygon_visibility_2`	simple polygons	No	\(O(n)\)$ time and \(O(n)\)$ space	B. Joe and R. B. Simpson [4]
`Rotational_sweep_visibility_2`	polygons with holes	No	\(O(n\log n)\)$ time and \(O(n)\)$ space	T. Asano [1]
`Triangular_expansion_visibility_2`	polygons with holes	\(O(n)\)$ time and \(O(n)\)$ space	\(O(nh)\)$ time and \(O(n)\)$ space.	Bungiu et al. [2]