Chapter 39
Planar Parameterization of Triangulated Surface Meshes

Laurent Saboret, Pierre Alliez and Bruno Lévy

Table of Contents

39.1   Introduction

Parameterizing a surface amounts to finding a one-to-one mapping from a suitable domain to the surface. A good mapping is the one which minimizes either angle distortions (conformal parameterization) or area distortions (equiareal parameterization) in some sense. In this package, we focus on parameterizing triangulated surfaces which are homeomorphic to a disk, and on piecewise linear mappings onto a planar domain.

Although the main motivation behind the first parameterization methods was the application to texture mapping, it is now frequently used for mapping more sophisticated modulation signals (such as normal, transparency, reflection or light modulation maps), fitting scattered data, re-parameterizing spline surfaces, repairing CAD models, approximating surfaces and remeshing.

This CGAL package implements some of the state-of-the-art surface parameterization methods, such as least squares conformal maps, discrete conformal map, discrete authalic parameterization, Floater mean value coordinates or Tutte barycentric mapping. These methods mainly distinguish by the distortion they minimize (angles vs. areas), by the constrained border onto the planar domain (convex polygon vs. free border) and by the guarantees provided in terms of bijective mapping.

The package proposes currently an interface with CGAL::Polyhedron_3<Traits> data structure.

Since parameterizing meshes require efficient representation of sparse matrices and efficient iterative or direct linear solvers, we provide a unified interface to state-of-the-art linear solver libraries (TAUCS), and propose a separate package devoted to OpenNL sparse linear solver.

Note that linear solvers commonly use double precision floating point numbers. Therefore, this package is intended to be used with a CGAL Cartesian kernel with doubles.

The intended audience of this package is researchers, developers or students developing algorithms around parameterization of triangle meshes for geometry processing as well as for signal mapping on triangulated surfaces.

Figure 39.1:  Texture mapping via Least Squares Conformal Maps parameterization. Top: original mesh and texture. Bottom: parameterized mesh (left: parameter space, right: textured mesh).

39.2   Basics

39.2.1   Default Surface Parameterization

From the user point of view, the simplest entry point to this package is the following function:

The function CGAL::parameterize() applies a default surface parameterization method: Floater Mean Value Coordinates [Flo03a], with an arc-length circular border parameterization, and using OpenNL sparse linear solver [Lev05]. The ParameterizationMesh_3 concept defines the input meshes handled by CGAL::parameterize(). See Section 39.2.2. The result is stored into the (u,v) fields of the mesh halfedges.

Note: CGAL::Parameterizer_traits_3<ParameterizationMesh_3> is the (pure virtual) superclass of all surface parameterizations and defines the error codes.

39.2.2   Input Mesh for parameterize()

The input meshes handled directly by CGAL::parameterize() must be models of ParameterizationMesh_3, triangulated, 2-manifold, oriented, and homeomorphic to discs (possibly with holes).

Note: ParameterizationMesh_3 is a general concept to access a polyhedral mesh. It is optimized for the Surface_mesh_parameterization package only in the sense that it defines the accessors to fields specific to the parameterization domain (index, u, v, is_parameterized). The extra constraints needed by the surface parameterization methods (triangulated, 2-manifold, homeomorphic to a disc) are not part of the concept and are checked at runtime.

This package provides a model of the ParameterizationMesh_3 concept to access CGAL::Polyhedron_3<Traits>:
CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron_3_>

We will see later that CGAL::parameterize() can support indirectly meshes that are not topological disks.

39.2.3   Default Parameterization Example

Simple_parameterization.cpp applies the default parameterization to a CGAL::Polyhedron_3<Traits> mesh (must be a topological disk). Eventually, it extracts the result from halfedges and prints it.

File: examples/Surface_mesh_parameterization/Simple_parameterization.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/Parameterization_polyhedron_adaptor_3.h>
#include <CGAL/parameterize.h>

#include <iostream>
#include <fstream>


// ----------------------------------------------------------------------------
// Private types
// ----------------------------------------------------------------------------

typedef CGAL::Cartesian<double>             Kernel;
typedef CGAL::Polyhedron_3<Kernel>          Polyhedron;


// ----------------------------------------------------------------------------
// main()
// ----------------------------------------------------------------------------

int main(int argc, char * argv[])
{
    std::cerr << "PARAMETERIZATION" << std::endl;
    std::cerr << "  Floater parameterization" << std::endl;
    std::cerr << "  Circle border" << std::endl;
    std::cerr << "  OpenNL solver" << std::endl;

    //***************************************
    // decode parameters
    //***************************************

    if (argc-1 != 1)
    {
        std::cerr << "Usage: " << argv[0] << " input_file.off" << std::endl;
        return(EXIT_FAILURE);
    }

    // File name is:
    const char* input_filename  = argv[1];

    //***************************************
    // Read the mesh
    //***************************************

    // Read the mesh
    std::ifstream stream(input_filename);
    Polyhedron mesh;
    stream >> mesh;
    if(!stream || !mesh.is_valid() || mesh.empty())
    {
        std::cerr << "FATAL ERROR: cannot read OFF file " << input_filename << std::endl;
        return EXIT_FAILURE;
    }

    //***************************************
    // Create Polyhedron adaptor
    // Note: no cutting => we support only
    // meshes that are topological disks
    //***************************************

    typedef CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron>
                                            Parameterization_polyhedron_adaptor;
    Parameterization_polyhedron_adaptor mesh_adaptor(mesh);

    //***************************************
    // Floater Mean Value Coordinates parameterization
    // (defaults are circular border and OpenNL solver)
    //***************************************

    // Type that defines the error codes
    typedef CGAL::Parameterizer_traits_3<Parameterization_polyhedron_adaptor>
                                            Parameterizer;

    Parameterizer::Error_code err = CGAL::parameterize(mesh_adaptor);
    if (err != Parameterizer::OK)
        std::cerr << "FATAL ERROR: " << Parameterizer::get_error_message(err) << std::endl;

    //***************************************
    // Output
    //***************************************

    if (err == Parameterizer::OK)
    {
        // Raw output: dump (u,v) pairs
        Polyhedron::Vertex_const_iterator pVertex;
        for (pVertex = mesh.vertices_begin();
            pVertex != mesh.vertices_end();
            pVertex++)
        {
            // (u,v) pair is stored in any halfedge
            double u = mesh_adaptor.info(pVertex->halfedge())->uv().x();
            double v = mesh_adaptor.info(pVertex->halfedge())->uv().y();
            std::cout << "(u,v) = (" << u << "," << v << ")" << std::endl;
        }
    }

    return (err == Parameterizer::OK) ? EXIT_SUCCESS : EXIT_FAILURE;
}

39.2.4   Enhanced parameterize() function

This package provides a second CGAL::parameterize() entry point where the user can specify a parameterization method:

39.2.5   Introduction to the Package Concepts

The ParameterizerTraits_3 concept

This CGAL package implements some of the state-of-the-art surface parameterization methods, such as Least Squares Conformal Maps, Discrete Conformal Map, Discrete Authalic Parameterization, Floater Mean Value Coordinates or Tutte Barycentric Mapping. These methods are provided as models of the ParameterizerTraits_3 concept. See Section 39.3.

Each of these surface parameterization methods is templated by the input mesh type, a border parameterization and a solver:

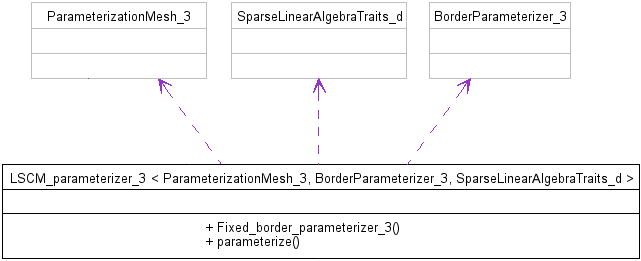
Figure 39.2:  A parameterizer UML class diagram (simplified).

The BorderParameterizer_3 concept

Parameterization methods for borders are used as traits classes modifying the behavior of ParameterizerTraits_3 models. They are provided as models of the BorderParameterizer_3 concept. See Sections 39.3.1.5 and 39.3.2.2.

The SparseLinearAlgebraTraits_d concept

This package solves sparse linear systems using solvers which are models of SparseLinearAlgebraTraits_d. See Section 39.4.

The ParameterizationMesh_3 and ParameterizationPatchableMesh_3 Concepts

As described in Section 39.2.2 the input meshes handled by CGAL::parameterize() must be models of the ParameterizationMesh_3 concept. The surface parameterization methods provided by this package only support surfaces which are homeomorphic to disks, possibly with holes. Nevertheless meshed with arbitrary topology and number of connected components can be parameterized, provided that the user specifies a cut graph (an oriented list of vertices) which is the border of a topological disc. If no cut graph is specified as input, the longest border of the input mesh is taken by default, the others being considered as holes.

For this purpose, the CGAL::Parameterization_mesh_patch_3<ParameterizationPatchableMesh_3> class is responsible for virtually cutting a patch into a ParameterizationPatchableMesh_3 mesh. The resulting patch is a topological disk (if the input cutting path is correct) and provides a ParameterizationMesh_3 interface. It can be used as parameter for the function CGAL::parameterize().

ParameterizationPatchableMesh_3 inherits from ParameterizationMesh_3, thus is a concept for a 3D surface mesh. ParameterizationPatchableMesh_3 adds the ability to support patches and virtual seams. Patches are a subset of a 3D mesh. Virtual seams behave as if the surface was cut along a cut graph. More information is provided in Section 39.5.

39.3   Surface Parameterization Methods

This CGAL package implements some of the state-of-the-art surface parameterization methods, such as Least Squares Conformal Maps, Discrete Conformal Map, Discrete Authalic Parameterization, Floater Mean Value Coordinates or Tutte Barycentric Mapping. These methods are provided as models of the ParameterizerTraits_3 concept.

39.3.1   Fixed Border Surface Parameterizations

Fixed Border Surface Parameterizations need a set of constraints: two (u,v) coordinates for each vertex along the border. Such border parameterizations are described in Section 39.3.1.5.

Tutte Barycentric Mapping

CGAL::Barycentric_mapping_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>

The Barycentric Mapping parameterization method has been introduced by Tutte [Tut63]. In parameter space, each vertex is placed at the barycenter of its neighbors to achieve the so-called convex combination condition. This algorithm amounts to solve one sparse linear solver for each set of parameter coordinates, with a #vertices x #vertices sparse and symmetric positive definite matrix (if the border vertices are eliminated from the linear system). A coefficient $$(i, j) of the matrix is set to 1 for an edge linking the vertex $$v_i to the vertex $$v_j, to minus the degree of the vertex $$v_i for a diagonal element, and to 0 for any other matrix entry. Although a bijective mapping is guaranteed when the border is convex, this method does not minimize angles nor areas distortion.

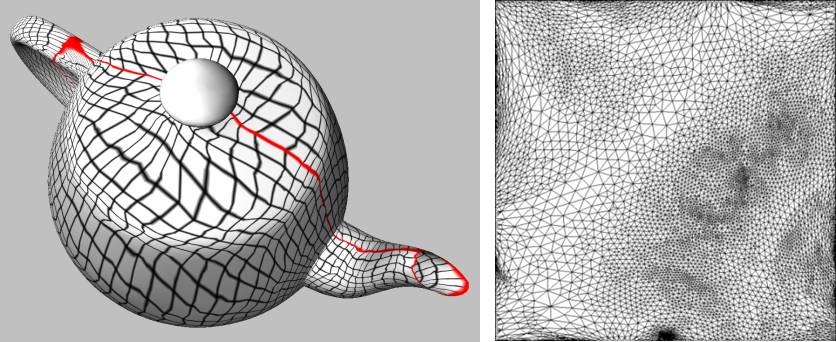
Figure 39.3:  Left: Tutte barycentric mapping parameterization (the red line depicts the cut graph). Right: parameter space.

Discrete Conformal Map

CGAL::Discrete_conformal_map_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>

Discrete conformal map parameterization has been introduced by Eck et al. to the graphics community [EDD$$⁺95]. It attempts to lower angle deformation by minimizing a discrete version of the Dirichlet energy as derived by Pinkall and Polthier [PP93]. A one-to-one mapping is guaranteed only when the two following conditions are fulfilled: the barycentric mapping condition (each vertex in parameter space is a convex combination if its neighboring vertices), and the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is sparse and symmetric definite positive (if the border vertices are eliminated from the linear system and if the mesh contains no hole), thus can be efficiently solved using dedicated linear solvers.

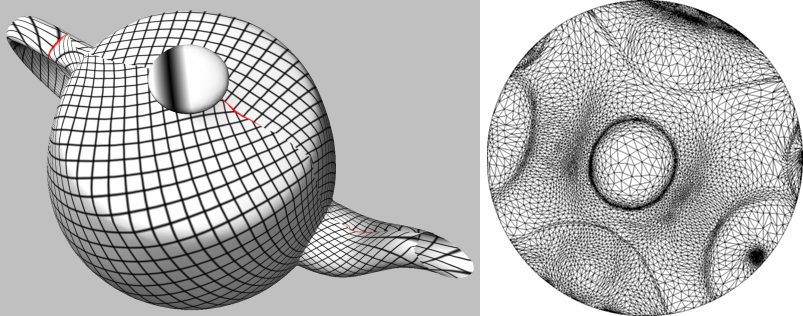
Figure 39.4:  Left: discrete conformal map. Right: parameter space.

Floater Mean Value Coordinates

CGAL::Mean_value_coordinates_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>

The mean value coordinates parameterization method has been introduced by Floater [Flo03a]. Each vertex in parameter space is optimized so as to be a convex combination of its neighboring vertices. The barycentric coordinates are this time unconditionally positive, by deriving an application of the mean theorem for harmonic functions. This method is in essence an approximation of the discrete conformal maps, with a guaranteed one-to-one mapping when the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is asymmetric.

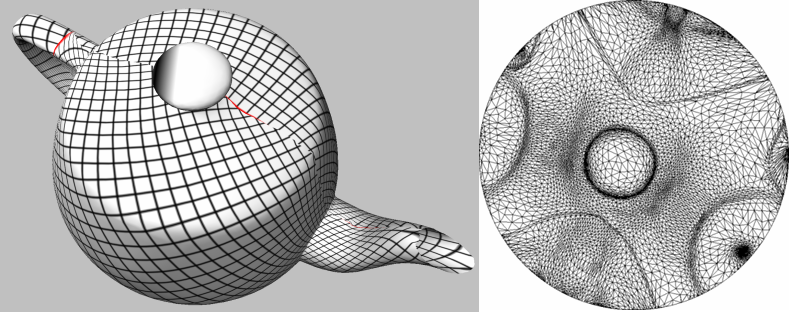
Figure 39.5:  Floater Mean Value Coordinates

Discrete Authalic parameterization

CGAL::Discrete_authalic_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>

The discrete authalic parameterization method has been introduced by Desbrun et al. [DMA02]. It corresponds to a weak formulation of an area-preserving method, and in essence locally minimizes the area distortion. A one-to-one mapping is guaranteed only if the convex combination condition is fulfilled and the border is convex. This method solves two #vertices x #vertices sparse linear systems. The matrix (the same for both systems) is asymmetric.

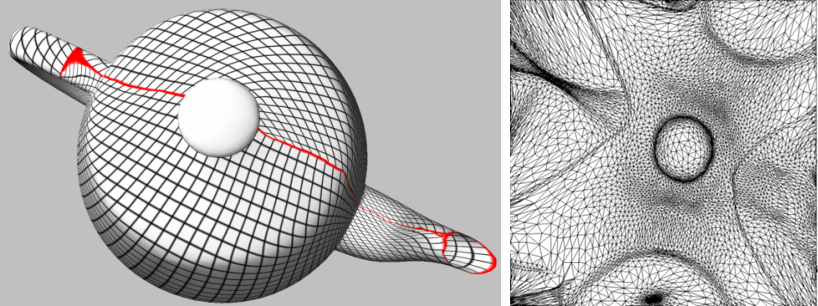
Figure 39.6:  Discrete Authalic Parameterization

Border Parameterizations for Fixed Methods

Parameterization methods for borders are used as traits classes modifying the behavior of ParameterizerTraits_3 models. They are provided as models of the BorderParameterizer_3 concept. Border parameterizations for fixed border surface parameterizations are a family of methods to define a set of constraints, namely two $$u,v coordinates for each vertex along the border.

• The user can select a border parameterization among two commonly used methods: uniform or arc-length parameterization.

  Usage:

  Uniform border parameterization is more stable, although it gives poor visual results. The arc-length border parameterization is used by default.

• One convex shape specified by one shape among two standard ones: a circle or a square.

  Usage:

  The circular border parameterization is used by default as it corresponds to the simplest convex shape. The square border parameterization is commonly used for texture mapping.

CGAL::Circular_border_arc_length_parameterizer_3<ParameterizationMesh_3>
CGAL::Circular_border_uniform_parameterizer_3<ParameterizationMesh_3>
CGAL::Square_border_arc_length_parameterizer_3<ParameterizationMesh_3>
CGAL::Square_border_uniform_parameterizer_3<ParameterizationMesh_3>

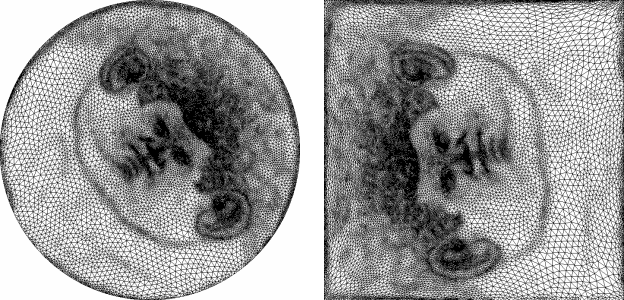
Figure 39.7:  Left: Julius Cesar mask parameterization with Authalic/circular border. Right: Julius Cesar mask's image with Floater/square border.

39.3.2   Free Border Surface Parameterizations

Least Squares Conformal Maps

CGAL::LSCM_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>

The Least Squares Conformal Maps (LSCM) parameterization method has been introduced by Lévy et al. [LPRM02]. It corresponds to a conformal method with a free border (at least two vertices have to be constrained to obtain a unique solution), which allows further lowering of the angle distortion. A one-to-one mapping is not guaranteed by this method. It solves a (2 $$ × #triangles) $$ × #vertices sparse linear system in the least squares sense, which implies solving a symmetric matrix.

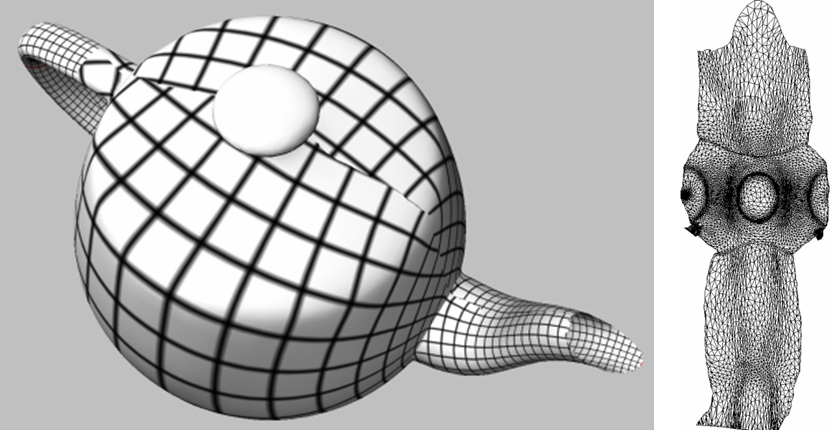
Figure 39.8:  Least squares conformal maps.

Border Parameterizations for Free Methods

Parameterization methods for borders are used as traits classes modifying the behavior of ParameterizerTraits_3 models. They are provided as models of the BorderParameterizer_3 concept. The border parameterizations associated to free border surface parameterization methods define only two constraints: the pinned vertices.

• CGAL::Two_vertices_parameterizer_3<ParameterizationMesh_3>
  

  Usage:

  CGAL::Two_vertices_parameterizer_3<ParameterizationMesh_3> is the default free border parameterization, and is the only one available in the current version of this package.

39.3.3   Discrete Authalic Parameterization Example

Authalic_parameterization.cpp computes a Discrete Authalic parameterization over a CGAL::Polyhedron_3<Traits> mesh. Specifying a specific surface parameterization instead of the default one means using the second parameter of CGAL::parameterize(). The differences with the first example Simple_parameterization.cpp are:

#include <CGAL/Discrete_authalic_parameterizer_3.h>

...

//***************************************
// Discrete Authalic Parameterization
//***************************************

typedef CGAL::Discrete_authalic_parameterizer_3<Parameterization_polyhedron_adaptor>
                                                    Parameterizer;

Parameterizer::Error_code err = CGAL::parameterize(mesh_adaptor, Parameterizer());

...

39.3.4   Square Border Arc Length Parameterization Example

Square_border_parameterization.cpp computes a Floater mean value coordinates parameterization with a square border arc length parameterization. Specifying a specific border parameterization instead of the default one means using the second parameter of CGAL::Mean_value_coordinates_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>. The differences with the first example Simple_parameterization.cpp are:

#include <CGAL/Square_border_parameterizer_3.h>

...

//***************************************
// Floater Mean Value Coordinates parameterization
// with square border
//***************************************

// Square border parameterizer
typedef CGAL::Square_border_arc_length_parameterizer_3<Parameterization_polyhedron_adaptor>
                                                        Border_parameterizer;

// Floater Mean Value Coordinates parameterizer with square border
typedef CGAL::Mean_value_coordinates_parameterizer_3<Parameterization_polyhedron_adaptor,
                                                        Border_parameterizer>
                                                    Parameterizer;

Parameterizer::Error_code err = CGAL::parameterize(mesh_adaptor, Parameterizer());

...

39.4   Sparse Linear Algebra

Parameterizing triangle meshes requires both efficient representation of sparse matrices and efficient iterative or direct linear solvers. We provide links to standard libraries (TAUCS) and include a separate package devoted to OpenNL sparse linear solver.

39.4.1   List of Solvers

We provide an interface to several sparse linear solvers, as models of the SparseLinearAlgebraTraits_d concept:

• OpenNL [Lev05] is shipped with CGAL. This is the default solver.

  OpenNL::DefaultLinearSolverTraits<COEFFTYPE, MATRIX, VECTOR, SOLVER> in OpenNL package
  OpenNL::SymmetricLinearSolverTraits<COEFFTYPE, MATRIX, VECTOR, SOLVER> in OpenNL package
  

  Usage:

  OpenNL (in the version shipped with CGAL) is a lightweight sparse linear solver. It does not support large systems, but it is highly portable and supports exact number types.

• TAUCS is a state-of-the-art direct solver for sparse symmetric matrices. It also includes an out-of-core general sparse solver.

  CGAL::Taucs_solver_traits<T>
  CGAL::Taucs_symmetric_solver_traits<T>
  

  Usage:

  TAUCS is very robust and supports large systems. On the other hand, it is not available on all platforms supported by CGAL and does not support exact number types.

  Install:

  TAUCS can be downloaded from http://www.tau.ac.il/~stoledo/taucs/2.2/taucs_full.zip.

39.4.2   TAUCS Solver Example

examples/Surface_mesh_parameterization/Taucs_parameterization.cpp computes the default parameterization method (Floater mean value coordinates with a circular border), but specifically instantiates the TAUCS solver. Specifying a specific solver instead of the default one (OpenNL) means using the third parameter of CGAL::Mean_value_coordinates_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d>. The differences with the first example examples/Surface_mesh_parameterization/Simple_parameterization.cpp are:

#include <CGAL/Taucs_solver_traits.h>

...

//***************************************
// Floater Mean Value Coordinates parameterization
// (circular border) with TAUCS solver
//***************************************

// Circular border parameterizer (the default)
typedef CGAL::Circular_border_arc_length_parameterizer_3<Parameterization_polyhedron_adaptor>
                                                    Border_parameterizer;
// TAUCS solver
typedef CGAL::Taucs_solver_traits<double>           Solver;

// Floater Mean Value Coordinates parameterization
// (circular border) with TAUCS solver
typedef CGAL::Mean_value_coordinates_parameterizer_3<Parameterization_polyhedron_adaptor,
                                                        Border_parameterizer,
                                                        Solver>
                                                    Parameterizer;

Parameterizer::Error_code err = CGAL::parameterize(mesh_adaptor, Parameterizer());

...

39.5   Cutting a Mesh

39.5.1   Computing a Cut Graph

All surface parameterization methods proposed in this package only deal with meshes which are homeomorphic (topologically equivalent) to discs. Nevertheless meshes with arbitrary topology and number of connected components car be parameterized, provided that the user specifies a cut graph (an oriented list of vertices), which is the border of a topological disc. If no cut graph is provided as input, the longest border already in the input mesh is taken as default border, all other borders being considered as holes. Note that only the inside part (i.e., one connected component) of the given border is parameterized.

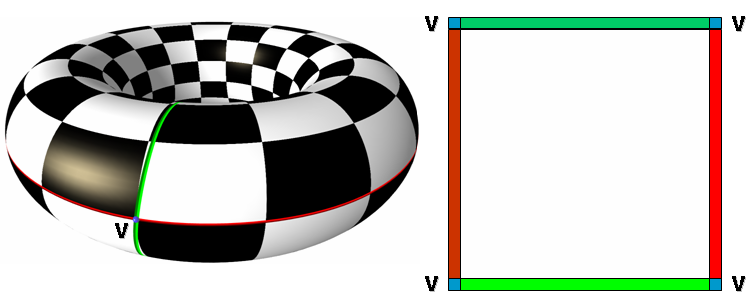
Figure 39.9:  Cut Graph

This package does not provide any algorithm to transform an arbitrary mesh into a topological disk, the user being responsible for generating such a cut graph. Nevertheless, we provide in polyhedron_ex_parameterization.cpp a simple cutting algorithm for the sake of completeness.

39.5.2   Applying a Cut

The surface parameterization classes in this package only directly support surfaces which are homeomorphic to disks (models of ParameterizationMesh_3). This software design simplifies the implementation of all new parameterization methods.

The CGAL::Parameterization_mesh_patch_3<ParameterizationPatchableMesh_3> class is responsible for virtually cutting a patch in a ParameterizationPatchableMesh_3 mesh. The resulting patch is a topological disk (if the cut graph is correct) and provides a ParameterizationMesh_3 interface. It can be used as parameter of CGAL::parameterize().

ParameterizationPatchableMesh_3 inherits from concept ParameterizationMesh_3, thus is a concept for a 3D surface mesh. ParameterizationPatchableMesh_3 adds the ability to support patches and virtual seams. Patches are a subset of a 3D mesh. Virtual seams behave exactly as if the surface was cut along a certain graph.

The ParameterizationMesh_3 interface with the Polyhedron is both a model of ParameterizationMesh_3 and ParameterizationPatchableMesh_3:
CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron_3_>

Note that this class is a decorator which adds on the fly the necessary fields to unmodified CGAL data structures (using STL maps). For better performances, it is recommended to use CGAL data structures enriched with the proper fields. See Polyhedron_ex class in polyhedron_ex_parameterization.cpp example.

39.5.3   Cutting a Mesh Example

Mesh_cutting_parameterization.cpp virtually cuts a CGAL::Polyhedron_3<Traits> mesh to make it a topological disk, then applies the default parameterization:

File: examples/Surface_mesh_parameterization/Mesh_cutting_parameterization.cpp

#include <CGAL/Cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/Parameterization_polyhedron_adaptor_3.h>
#include <CGAL/parameterize.h>
#include <CGAL/Parameterization_mesh_patch_3.h>

#include <iostream>
#include <fstream>


// ----------------------------------------------------------------------------
// Private types
// ----------------------------------------------------------------------------

typedef CGAL::Cartesian<double>             Kernel;
typedef CGAL::Polyhedron_3<Kernel>          Polyhedron;

// Polyhedron adaptor
typedef CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron>
                                            Parameterization_polyhedron_adaptor;

// Type describing a border or seam as a vertex list
typedef std::list<Parameterization_polyhedron_adaptor::Vertex_handle>
                                            Seam;


// ----------------------------------------------------------------------------
// Private functions
// ----------------------------------------------------------------------------

// If the mesh is a topological disk, extract its longest border,
// else compute a very simple cut to make it homeomorphic to a disk.
// Return the border of this region (empty on error)
//
// CAUTION: this cutting algorithm is very naive. Write your own!
static Seam cut_mesh(Parameterization_polyhedron_adaptor& mesh_adaptor)
{
    // Helper class to compute genus or extract borders
    typedef CGAL::Parameterization_mesh_feature_extractor<Parameterization_polyhedron_adaptor>
                                            Mesh_feature_extractor;

    Seam seam;              // returned list

    // Get reference to Polyhedron_3 mesh
    Polyhedron& mesh = mesh_adaptor.get_adapted_mesh();

    // Extract mesh borders and compute genus
    Mesh_feature_extractor feature_extractor(mesh_adaptor);
    int nb_borders = feature_extractor.get_nb_borders();
    int genus = feature_extractor.get_genus();

    // If mesh is a topological disk
    if (genus == 0 && nb_borders > 0)
    {
        // Pick the longest border
        seam = feature_extractor.get_longest_border();
    }
    else // if mesh is NOT a topological disk, create a virtual cut
    {
        const int CUT_LENGTH = 6;

        // Build consecutive halfedges array
        Polyhedron::Halfedge_handle seam_halfedges[CUT_LENGTH];
        seam_halfedges[0] = mesh.halfedges_begin();
        if (seam_halfedges[0] == NULL)
            return seam;                    // return empty list
        int i;
        for (i=1; i<CUT_LENGTH; i++)
        {
            seam_halfedges[i] = seam_halfedges[i-1]->next()->opposite()->next();
            if (seam_halfedges[i] == NULL)
                return seam;                // return empty list
        }

        // Convert halfedges array to two-ways vertices list
        for (i=0; i<CUT_LENGTH; i++)
            seam.push_back(seam_halfedges[i]->vertex());
        for (i=CUT_LENGTH-1; i>=0; i--)
            seam.push_back(seam_halfedges[i]->opposite()->vertex());
    }

    return seam;
}


// ----------------------------------------------------------------------------
// main()
// ----------------------------------------------------------------------------

int main(int argc, char * argv[])
{
    std::cerr << "PARAMETERIZATION" << std::endl;
    std::cerr << "  Floater parameterization" << std::endl;
    std::cerr << "  Circle border" << std::endl;
    std::cerr << "  OpenNL solver" << std::endl;
    std::cerr << "  Very simple cut if model is not a topological disk" << std::endl;

    //***************************************
    // decode parameters
    //***************************************

    if (argc-1 != 1)
    {
        std::cerr << "Usage: " << argv[0] << " input_file.off" << std::endl;
        return(EXIT_FAILURE);
    }

    // File name is:
    const char* input_filename  = argv[1];

    //***************************************
    // Read the mesh
    //***************************************

    // Read the mesh
    std::ifstream stream(input_filename);
    Polyhedron mesh;
    stream >> mesh;
    if(!stream || !mesh.is_valid() || mesh.empty())
    {
        std::cerr << "FATAL ERROR: cannot read OFF file " << input_filename << std::endl;
        return EXIT_FAILURE;
    }

    //***************************************
    // Create Polyhedron adaptor
    //***************************************

    Parameterization_polyhedron_adaptor mesh_adaptor(mesh);

    //***************************************
    // Virtually cut mesh
    //***************************************

    // The parameterization methods support only meshes that
    // are topological disks => we need to compute a "cutting" of the mesh
    // that makes it homeomorphic to a disk
    Seam seam = cut_mesh(mesh_adaptor);
    if (seam.empty())
    {
        std::cerr << "FATAL ERROR: an unexpected error occurred while cutting the shape" << std::endl;
        return EXIT_FAILURE;
    }

    // Create a second adaptor that virtually "cuts" the mesh following the 'seam' path
    typedef CGAL::Parameterization_mesh_patch_3<Parameterization_polyhedron_adaptor>
                                            Mesh_patch_polyhedron;
    Mesh_patch_polyhedron   mesh_patch(mesh_adaptor, seam.begin(), seam.end());
    if (!mesh_patch.is_valid())
    {
        std::cerr << "FATAL ERROR: non manifold shape or invalid cutting" << std::endl;
        return EXIT_FAILURE;
    }

    //***************************************
    // Floater Mean Value Coordinates parameterization
    //***************************************

    // Type that defines the error codes
    typedef CGAL::Parameterizer_traits_3<Mesh_patch_polyhedron>
                                            Parameterizer;

    Parameterizer::Error_code err = CGAL::parameterize(mesh_patch);
    if (err != Parameterizer::OK)
        std::cerr << "FATAL ERROR: " << Parameterizer::get_error_message(err) << std::endl;

    //***************************************
    // Output
    //***************************************

    if (err == Parameterizer::OK)
    {
        // Raw output: dump (u,v) pairs
        Polyhedron::Vertex_const_iterator pVertex;
        for (pVertex = mesh.vertices_begin();
            pVertex != mesh.vertices_end();
            pVertex++)
        {
            // (u,v) pair is stored in any halfedge
            double u = mesh_adaptor.info(pVertex->halfedge())->uv().x();
            double v = mesh_adaptor.info(pVertex->halfedge())->uv().y();
            std::cout << "(u,v) = (" << u << "," << v << ")" << std::endl;
        }
    }

    return (err == Parameterizer::OK) ? EXIT_SUCCESS : EXIT_FAILURE;
}

39.6   Output

Parameterization methods compute $$(u,v) fields for each vertex of the input mesh, with the seam vertices being virtually duplicated (thanks to CGAL::Parameterization_mesh_patch_3<ParameterizationPatchableMesh_3>). To support this duplication, CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron_3_> stores the result in the $$(u,v) fields of the input mesh halfedges. A $$(u,v) pair is computed for each inner vertex (i.e. its halfedges share the same $$(u,v) pair), while a $$(u,v) pair is computed for each border halfedge. The user has to iterate over the mesh halfedges to get the result. Note that $$(u,v) fields do not exist in CGAL::Polyhedron_3<Traits>, thus the output traversal is specific to the way the (u,v) fields are implemented by the adaptor.

39.6.1   EPS Output Example

Complete_parameterization_example.cpp is a complete parameterization example which outputs the resulting parameterization to a EPS file. It gets the $$(u,v) fields computed by a parameterization method over a CGAL::Polyhedron_3<Traits> mesh with a CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron_3_> adaptor:

File: examples/Surface_mesh_parameterization/Complete_parameterization_example.cpp

#include <CGAL/basic.h> // include basic.h before testing #defines

#ifdef CGAL_USE_TAUCS


#include <CGAL/Cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/Parameterization_polyhedron_adaptor_3.h>
#include <CGAL/parameterize.h>
#include <CGAL/Discrete_authalic_parameterizer_3.h>
#include <CGAL/Square_border_parameterizer_3.h>
#include <CGAL/Parameterization_mesh_patch_3.h>

#include <CGAL/Taucs_solver_traits.h>

#include <iostream>
#include <fstream>
#include <cstdlib>


// ----------------------------------------------------------------------------
// Private types
// ----------------------------------------------------------------------------

typedef CGAL::Cartesian<double>             Kernel;
typedef CGAL::Polyhedron_3<Kernel>          Polyhedron;

// Polyhedron adaptor
typedef CGAL::Parameterization_polyhedron_adaptor_3<Polyhedron>
                                            Parameterization_polyhedron_adaptor;

// Type describing a border or seam as a vertex list
typedef std::list<Parameterization_polyhedron_adaptor::Vertex_handle>
                                            Seam;


// ----------------------------------------------------------------------------
// Private functions
// ----------------------------------------------------------------------------

// If the mesh is a topological disk, extract its longest border,
// else compute a very simple cut to make it homeomorphic to a disk.
// Return the border of this region (empty on error)
//
// CAUTION: this cutting algorithm is very naive. Write your own!
static Seam cut_mesh(Parameterization_polyhedron_adaptor& mesh_adaptor)
{
    // Helper class to compute genus or extract borders
    typedef CGAL::Parameterization_mesh_feature_extractor<Parameterization_polyhedron_adaptor>
                                            Mesh_feature_extractor;

    Seam seam;              // returned list

    // Get reference to Polyhedron_3 mesh
    Polyhedron& mesh = mesh_adaptor.get_adapted_mesh();

    // Extract mesh borders and compute genus
    Mesh_feature_extractor feature_extractor(mesh_adaptor);
    int nb_borders = feature_extractor.get_nb_borders();
    int genus = feature_extractor.get_genus();

    // If mesh is a topological disk
    if (genus == 0 && nb_borders > 0)
    {
        // Pick the longest border
        seam = feature_extractor.get_longest_border();
    }
    else // if mesh is NOT a topological disk, create a virtual cut
    {
        const int CUT_LENGTH = 6;

        // Build consecutive halfedges array
        Polyhedron::Halfedge_handle seam_halfedges[CUT_LENGTH];
        seam_halfedges[0] = mesh.halfedges_begin();
        if (seam_halfedges[0] == NULL)
            return seam;                    // return empty list
        int i;
        for (i=1; i<CUT_LENGTH; i++)
        {
            seam_halfedges[i] = seam_halfedges[i-1]->next()->opposite()->next();
            if (seam_halfedges[i] == NULL)
                return seam;                // return empty list
        }

        // Convert halfedges array to two-ways vertices list
        for (i=0; i<CUT_LENGTH; i++)
            seam.push_back(seam_halfedges[i]->vertex());
        for (i=CUT_LENGTH-1; i>=0; i--)
            seam.push_back(seam_halfedges[i]->opposite()->vertex());
    }

    return seam;
}

// Dump parameterized mesh to an eps file
static bool write_file_eps(const Parameterization_polyhedron_adaptor& mesh_adaptor,
                           const char *pFilename,
                           double scale = 500.0)
{
    const Polyhedron& mesh = mesh_adaptor.get_adapted_mesh();

    std::ofstream out(pFilename);
    if(!out)
        return false;
    CGAL::set_ascii_mode(out);

    // compute bounding box
    double xmin,xmax,ymin,ymax;
    xmin = ymin = xmax = ymax = 0;
    Polyhedron::Halfedge_const_iterator pHalfedge;
    for (pHalfedge = mesh.halfedges_begin();
         pHalfedge != mesh.halfedges_end();
         pHalfedge++)
    {
        double x1 = scale * mesh_adaptor.info(pHalfedge->prev())->uv().x();
        double y1 = scale * mesh_adaptor.info(pHalfedge->prev())->uv().y();
        double x2 = scale * mesh_adaptor.info(pHalfedge)->uv().x();
        double y2 = scale * mesh_adaptor.info(pHalfedge)->uv().y();
        xmin = (std::min)(xmin,x1);
        xmin = (std::min)(xmin,x2);
        xmax = (std::max)(xmax,x1);
        xmax = (std::max)(xmax,x2);
        ymax = (std::max)(ymax,y1);
        ymax = (std::max)(ymax,y2);
        ymin = (std::min)(ymin,y1);
        ymin = (std::min)(ymin,y2);
    }

    out << "%!PS-Adobe-2.0 EPSF-2.0" << std::endl;
    out << "%%BoundingBox: " << int(xmin+0.5) << " "
                                << int(ymin+0.5) << " "
                                << int(xmax+0.5) << " "
                                << int(ymax+0.5) << std::endl;
    out << "%%HiResBoundingBox: " << xmin << " "
                                    << ymin << " "
                                    << xmax << " "
                                    << ymax << std::endl;
    out << "%%EndComments" << std::endl;
    out << "gsave" << std::endl;
    out << "0.1 setlinewidth" << std::endl;

    // color macros
    out << std::endl;
    out << "% RGB color command - r g b C" << std::endl;
    out << "/C { setrgbcolor } bind def" << std::endl;
    out << "/white { 1 1 1 C } bind def" << std::endl;
    out << "/black { 0 0 0 C } bind def" << std::endl;

    // edge macro -> E
    out << std::endl;
    out << "% Black stroke - x1 y1 x2 y2 E" << std::endl;
    out << "/E {moveto lineto stroke} bind def" << std::endl;
    out << "black" << std::endl << std::endl;

    // for each halfedge
    for (pHalfedge = mesh.halfedges_begin();
         pHalfedge != mesh.halfedges_end();
         pHalfedge++)
    {
        double x1 = scale * mesh_adaptor.info(pHalfedge->prev())->uv().x();
        double y1 = scale * mesh_adaptor.info(pHalfedge->prev())->uv().y();
        double x2 = scale * mesh_adaptor.info(pHalfedge)->uv().x();
        double y2 = scale * mesh_adaptor.info(pHalfedge)->uv().y();
        out << x1 << " " << y1 << " " << x2 << " " << y2 << " E" << std::endl;
    }

    /* Emit EPS trailer. */
    out << "grestore" << std::endl;
    out << std::endl;
    out << "showpage" << std::endl;

    return true;
}


// ----------------------------------------------------------------------------
// main()
// ----------------------------------------------------------------------------

int main(int argc, char * argv[])
{
    std::cerr << "PARAMETERIZATION" << std::endl;
    std::cerr << "  Discrete Authalic Parameterization" << std::endl;
    std::cerr << "  Square border" << std::endl;
    std::cerr << "  TAUCS solver" << std::endl;
    std::cerr << "  Very simple cut if model is not a topological disk" << std::endl;
    std::cerr << "  Output: EPS" << std::endl;

    //***************************************
    // decode parameters
    //***************************************

    if (argc-1 != 2)
    {
        std::cerr << "Usage: " << argv[0] << " input_file.off output_file.eps" << std::endl;
        return(EXIT_FAILURE);
    }

    // File names are:
    const char* input_filename  = argv[1];
    const char* output_filename = argv[2];

    //***************************************
    // Read the mesh
    //***************************************

    // Read the mesh
    std::ifstream stream(input_filename);
    Polyhedron mesh;
    stream >> mesh;
    if(!stream || !mesh.is_valid() || mesh.empty())
    {
        std::cerr << "FATAL ERROR: cannot read OFF file " << input_filename << std::endl;
        return EXIT_FAILURE;
    }

    //***************************************
    // Create Polyhedron adaptor
    //***************************************

    Parameterization_polyhedron_adaptor mesh_adaptor(mesh);

    //***************************************
    // Virtually cut mesh
    //***************************************

    // The parameterization methods support only meshes that
    // are topological disks => we need to compute a "cutting" of the mesh
    // that makes it homeomorphic to a disk
    Seam seam = cut_mesh(mesh_adaptor);
    if (seam.empty())
    {
        std::cerr << "FATAL ERROR: an unexpected error occurred while cutting the shape" << std::endl;
        return EXIT_FAILURE;
    }

    // Create a second adaptor that virtually "cuts" the mesh following the 'seam' path
    typedef CGAL::Parameterization_mesh_patch_3<Parameterization_polyhedron_adaptor>
                                            Mesh_patch_polyhedron;
    Mesh_patch_polyhedron   mesh_patch(mesh_adaptor, seam.begin(), seam.end());
    if (!mesh_patch.is_valid())
    {
        std::cerr << "FATAL ERROR: non manifold shape or invalid cutting" << std::endl;
        return EXIT_FAILURE;
    }

    //***************************************
    // Discrete Authalic Parameterization (square border)
    // with TAUCS solver
    //***************************************

    // Border parameterizer
    typedef CGAL::Square_border_arc_length_parameterizer_3<Mesh_patch_polyhedron>
                                                            Border_parameterizer;
    // TAUCS solver
    typedef CGAL::Taucs_solver_traits<double>               Solver;

    // Discrete Authalic Parameterization (square border)
    // with TAUCS solver
    typedef CGAL::Discrete_authalic_parameterizer_3<Mesh_patch_polyhedron,
                                                    Border_parameterizer,
                                                    Solver> Parameterizer;

    Parameterizer::Error_code err = CGAL::parameterize(mesh_patch, Parameterizer());
    if (err != Parameterizer::OK)
        std::cerr << "FATAL ERROR: " << Parameterizer::get_error_message(err) << std::endl;

    //***************************************
    // Output
    //***************************************

    // Write Postscript file
    if (err == Parameterizer::OK)
    {
        if ( ! write_file_eps(mesh_adaptor, output_filename) )
        {
            std::cerr << "FATAL ERROR: cannot write file " << output_filename << std::endl;
            return EXIT_FAILURE;
        }
    }

    return (err == Parameterizer::OK) ? EXIT_SUCCESS : EXIT_FAILURE;
}


#else // CGAL_USE_TAUCS


#include <iostream>
#include <cstdlib>

// ----------------------------------------------------------------------------
// Empty main() if TAUCS is not installed
// ----------------------------------------------------------------------------

int main()
{
    std::cerr << "Skip test as TAUCS is not installed" << std::endl;
    return EXIT_SUCCESS;
}

#endif // CGAL_USE_TAUCS

39.7   Complexity and Guarantees

39.7.1   Parameterization Methods and Guarantees

• Fixed boundaries

  • One-to-one mapping

    Tutte's theorem guarantees a one-to-one mapping provided that the weights are all positive and the border convex. It is the case for Tutte barycentric mapping and Floater mean value coordinates. It is not always the case for discrete conformal map (cotangents) and discrete authalic parameterization.

  • Non-singularity of the matrix

    Geshorgin's theorem guarantees the convergence of the solver if the matrix is diagonal dominant. This is the case with positive weights (Tutte barycentric mapping and Floater mean value coordinates).

• Free boundaries

  • One-to-one mapping

    No guarantee is provided by LSCM (both global overlaps and triangle flips can occur).

  • Non-singularity of the matrix

    For LSCM, the matrix of the system is the Gram matrix of a matrix with maximal rank, and is therefore non-singular (Gram theorem).

39.7.2   Precision

Two algorithms of this package construct the sparse linear system(s) using trigonometric functions, and are this incompatible with exact arithmetic:

• Floater mean value coordinates

• Circular border parameterization

On the other hand, linear solvers commonly use double precision floating point numbers.
OpenNL's BICGSTAB solver (accessible through the OpenNL::DefaultLinearSolverTraits<COEFFTYPE, MATRIX, VECTOR, SOLVER> interface) is the only solver supported by this package which computes exact results, when used with an exact arithmetic. This package is intended to be used mainly with a CGAL Cartesian kernel with doubles.

OpenNL's BICGSTAB Solver with an Exact Arithmetic

The BICGSTAB conjugate gradient is in disguise a direct solver. In a nutshell, it computes a vector basis orthogonal with respect to the matrix, and the coordinates of the solution in this vector basis. Each iteration computes one component of the basis and one coordinate, therefore the algorithm converges to the solution in $$n iterations, where $$n is the dimension of the matrix. More precisely, it is shown to converge in $$k iteration, where $$k is the number of distinct eigenvalues of the matrix.

Solvers with a Floating Point Arithmetic

OpenNL's BICGSTAB example:

When inexact numerical types are used (e.g. doubles), accumulated errors slow down convergence (in practice, it requires approximately $$5k iterations to converge). The required number of iterations depends on the eigenvalues of the matrix, and these eigenvalues depend on the shape of the triangles. The optimum is when the triangles are equilateral (then the solver converges in less than 10 iterations). The worst case is obtained when the mesh has a large number of skinny triangles (near-singular Jacobian matrix of the triangle). In this case, the spectrum of the matrix is wide (many different eigenvalues), and the solver requires nearly $$5n iterations to converge.

39.7.3   Algorithmic Complexity

In this package, we focus on piecewise linear mappings onto a planar domain. All surface parameterization methods are based on solving one (or two) sparse linear system(s). The algorithmic complexity is dominated by the resolution of the sparse linear system(s).

OpenNL's BICGSTAB example:

At each iteration, the operation of highest complexity is the product between the sparse-matrix and a vector. The sparse matrix has a fixed number of non-zero coefficients per row, therefore the matrix / vector product has $$O(n) complexity. Since convergence is reached after $$k iterations, the complexity is $$O(k.n) (where $$k is the number of distinct eigenvalues of the matrix). Therefore, best case complexity is $$O(n) (equilateral triangles), and worst case complexity is $$O(n²) (skinny triangles).

39.8   Software Design

39.8.1   Global Function parameterize()

This package's entry point is:

// Compute a one-to-one mapping from a 3D triangle surface 'mesh' to a
// 2D circle, using Floater Mean Value Coordinates algorithm.
// A one-to-one mapping is guaranteed.
template <class ParameterizationMesh_3>
typename Parameterizer_traits_3<ParameterizationMesh_3>::Error_code
parameterize(ParameterizationMesh_3& mesh)  // 3D mesh, model of ParameterizationMesh_3 concept
{
    Mean_value_coordinates_parameterizer_3<ParameterizationMesh_3> parameterizer;
    return parameterizer.parameterize(mesh);
}

// Compute a one-to-one mapping from a 3D triangle surface 'mesh' to a
// simple 2D domain.
// One-to-one mapping may be guaranteed or not,
// depending on the chosen ParametizerTraits_3 algorithm.
template <class ParameterizationMesh_3, class ParameterizerTraits_3>
typename Parameterizer_traits_3<ParameterizationMesh_3>::Error_code
parameterize(ParameterizationMesh_3& mesh,          // 3D mesh, model of ParameterizationMesh_3
             ParameterizerTraits_3 parameterizer)   // Parameterization method for 'mesh'
{
    return parameterizer.parameterize(mesh);
}

You may notice that these global functions simply call the parameterize() method of a ParameterizerTraits_3 object. The purpose of these global functions is:

• to be consistent with other CGAL algorithms that are also provided as global functions, e.g. CGAL::convex_hull_2(),
• to provide a default parameterization method (Floater Mean Value Coordinates), which wouldn't be possible with a direct call to an object's method.

You may also wonder why there is not just one CGAL::parameterize() function with a default ParameterizerTraits_3 argument equal to CGAL::Mean_value_coordinates_parameterizer_3<ParameterizationMesh_3>. The reason is simply that this is not allowed by the C++ standard (see [C++98], paragraph 14.1/9).

39.8.2   No Common Parameterization Algorithm

ParameterizerTraits_3 models modify the behavior of the global function CGAL::parameterize() - hence the Traits in the name. On the other hand, ParameterizerTraits_3 models do not modify the behavior of a common parameterization algorithm - as you might expect.

In this package, we focus on triangulated surfaces that are homeomorphic to a disk and on piecewise linear mappings onto planar domains. A consequence is that the skeleton of all parameterization methods of this package is the same:

• Allocate a sparse linear system $$A.X = B
• Parameterize the mesh border and initialize $$B
• Parameterize the inner points of the mesh and set $$A coefficients
• Solve the system

It is tempting to make the parameterization method a traits class that modifies the behavior of a common parameterization algorithm. On the other hand, there are several differences among methods:

• Fixed border methods need to parameterize all border vertices, while free border methods parameterize only two vertices.
• Some methods create symmetric definite positive systems, which may be solved more efficiently than general systems.
• Most parameterization methods use two #vertices x #vertices systems, where Least Squares Conformal Maps uses one (2 * #triangles) x #vertices system.
• Most parameterization methods invert the $$A matrix, when Least Squares Conformal Maps solves the system in the least squares sense.

Therefore, the software design chosen is:

• Each ParameterizerTraits_3 model implements its own version of the parameterization algorithm as a parameterize() method.
• Each ParameterizerTraits_3 model has template arguments defining the border parameterization and sparse linear solver to use, with default values adapted to the method.
• Code factorization is achieved using a class hierarchy and (few) virtual methods.

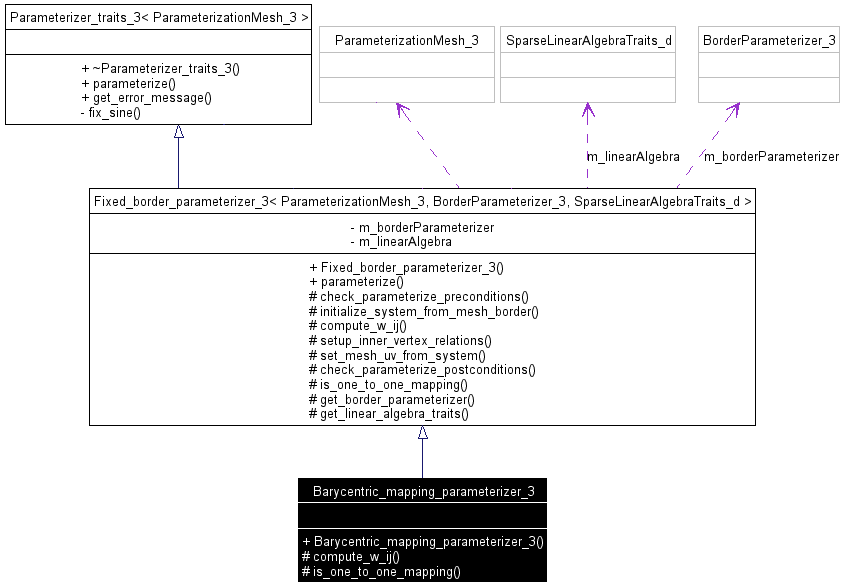
Figure 39.10:  A parameterizer UML class diagram (main types and methods only)

Figure 39.11:  Surface parameterizer classes hierarchy

Note: CGAL::Parameterizer_traits_3<ParameterizationMesh_3> is the (pure virtual) superclass of all surface parameterization classes.

39.8.3   Fixed_border_parameterizer_3 Class

Linear fixed border parameterization algorithms are very close. They mainly differ by the energy that they try to minimize, i.e. by the value of the $$w_ij coefficient of the $$A matrix, for $$v_i and $$v_j neighbor vertices of the mesh [FH05]. One consequence is that most of the code of the fixed border methods is factorized in the CGAL::Fixed_border_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d> class.

Subclasses:

• must provide BorderParameterizer_3 and SparseLinearAlgebraTraits_d default template parameters that make sense,
• must implement compute_w_ij() to compute $$w_ij = (i, j) coefficient of matrix $$A for $$v_j neighbor vertex of $$v_i,
• may implement an optimized version of is_one_to_one_mapping().

See CGAL::Barycentric_mapping_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d> class as an example.

39.8.4   Border Parameterizations

Border Parameterizations are models of the BorderParameterizer_3 concept. To simplify the implementation, BorderParameterizer_3 models know only the ParameterizationMesh_3 mesh class. They do not know the parameterization algorithm or the sparse linear solver used.

39.8.5   ParameterizationMesh_3 and ParameterizationPatchableMesh_3 Concepts

All parameterization methods are templated by the kind of mesh they are applied on. The mesh type must be a model of ParameterizationMesh_3.

The purpose of such a model is to:

1. Support several kind of meshes.
2. Hide the implementation of extra fields specific to the parameterization domain (index, u, v, is_parameterized).
3. Handle in the mesh type the complexity of virtually cutting a mesh to make it homeomorphic to a disk (instead of duplicating this code in each parameterization method).

Two options are possible for 1) and 2):

• Pass to all classes and methods a mesh pointer, a traits class to manipulate it, and accessors to the extra field arrays. This is the choice of the Boost Graph Library with boost::graph_traits<> and the property maps.
• Pass to all classes and methods an object that points to the actual mesh and knows how to access to its fields. This is the Adaptor concept [GHJV95].

The current design of this package uses the second option, which is simpler. Of course, we may decide at some point to switch to the first one to reach a deeper integration of CGAL with Boost.

Point 3) is solved by class CGAL::Parameterization_mesh_patch_3<ParameterizationPatchableMesh_3>, which takes care of virtually cutting a patch in a ParameterizationPatchableMesh_3 mesh, to make it appear as a topological disk with a ParameterizationMesh_3 interface. ParameterizationPatchableMesh_3 inherits from concept ParameterizationMesh_3 and adds the ability to support patches and virtual seams.

This mainly means that:

• vertices can be tagged as inside or outside the patch to parameterize,
• the fields specific to parameterizations (index, u, v, is_parameterized) can be set per corner (which is a more general way of saying per half-edge).

39.8.6   SparseLinearAlgebraTraits_d Concept

This package solves sparse linear systems using solvers which are models of SparseLinearAlgebraTraits_d.

SparseLinearAlgebraTraits_d is a sub-concept of the LinearAlgebraTraits_d concept in Kernel_d. The goal is to adapt easily code written for dense matrices to sparse ones, and vice-versa.

39.8.7   Cutting a Mesh

In this package, we focus on triangulated surfaces that are homeomorphic to a disk.

Computing a cutting path that transforms a closed mesh of arbitrary genus into a topological disk is a research topic on its own. This package does not intend to cover this topic at the moment.

39.9   Extending the Package and Reusing Code

39.9.1   Reusing Mesh Adaptors

ParameterizationMesh_3 defines a concept to access to a general polyhedral mesh. It is optimized for the Surface_mesh_parameterization package only in the sense that it defines the accessors to fields specific to the parameterization domain (index, u, v, is_parameterized).

It may be easily generalized.

39.9.2   Reusing Sparse Linear Algebra

The SparseLinearAlgebraTraits_d concept and the traits classes for OpenNL and TAUCS are independent of the rest of the Surface_mesh_parameterization package, and may be reused by CGAL developers for other purposes.

39.9.3   Adding New Parameterization Methods

Implementing a new fixed border linear parameterization is easy. Most of the code of the fixed border methods is factorized in the CGAL::Fixed_border_parameterizer_3<ParameterizationMesh_3, BorderParameterizer_3, SparseLinearAlgebraTraits_d> class. Subclasses must mainly implement a compute_w_ij() method which computes each $$w_ij = $$(i, j) coefficient of the matrix $$A for $$v_j neighboring vertices of $$v_i.

Although implementing a new free border linear parameterization method is more challenging, the Least Squares Conformal Maps parameterization method provides a good starting point.

Implementing non linear parameterizations is a natural extension to this package, although only the mesh adaptors can be reused.

39.9.4   Adding New Border Parameterization Methods

Implementing a new border parameterization method is easy. Square, circular and two-points border parameterizations are good starting points.

39.9.5   Mesh Cutting

Obviously, this package would benefit of having robust algorithms which transform arbitrary meshes into topological disks.