|
CGAL 6.1 - Halfedge Data Structures
|
|
CGAL 6.1 - Halfedge Data Structures
|
A halfedge data structure (abbreviated as HalfedgeDS, or HDS for template parameters) is an edge-centered data structure capable of maintaining incidence information of vertices, edges and faces, for example for planar maps, polyhedra, or other orientable, two-dimensional surfaces embedded in arbitrary dimension. Each edge is decomposed into two halfedges with opposite orientations. One incident face and one incident vertex are stored in each halfedge. For each face and each vertex, one incident halfedge is stored. Reduced variants of the halfedge data structure can omit some of these information, for example the halfedge pointers in faces or the storage of faces at all.
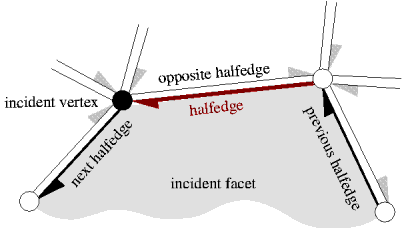
The halfedge data structure is a combinatorial data structure, geometric interpretation is added by classes built on top of the halfedge data structure. These classes might be more convenient to use than the halfedge data structure directly, since the halfedge data structure is meant as an implementation layer. See for example the Polyhedron_3 class in Chapter Polyhedral Surface.
The data structure provided here is also known as the FE-structure [9], as halfedges [6], [2] or as the doubly connected edge list (DCEL) [3], although the original reference for the DCEL [7] describes a different data structure. The halfedge data structure can also be seen as one of the variants of the quad-edge data structure [4]. In general, the quad-edge data can represent non-orientable 2-manifolds, but the variant here is restricted to orientable 2-manifolds only. An overview and comparison of these different data structures together with a thorough description of the design implemented here can be found in [5].
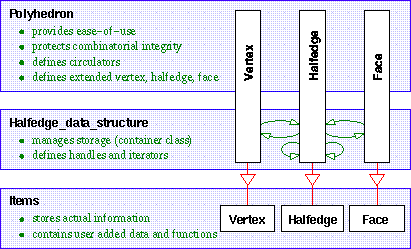
Figure 28.1 Responsibilities of the different layers in the halfedge data-structure design.
Figure 28.1 illustrates the responsibilities of the three layers of the software design, with the Polyhedron_3 as an example for the top layer. The items provide the space for the information that is actually stored, i.e., with member variables and access member functions in Vertex, Halfedge, and Face respectively. Halfedges are required to provide a reference to the next halfedge and to the opposite halfedge. Optionally they may provide a reference to the previous halfedge, to the incident vertex, and to the incident face. Vertices and faces may be empty. Optionally they may provide a reference to the incident halfedge. The options mentioned are supported in the halfedge data structure and the polyhedron, for example, Euler operations update the optional references if they are present. Furthermore, the item classes can be extended with arbitrary attributes and member functions, which will be promoted by inheritance to the actual classes used for the polyhedron.
Vertices, halfedges, and faces are passed as local types of the Items class to the halfedge data structure and polyhedron. Implementations for vertices, halfedges and faces are provided that fulfill the mandatory part of the requirements. They can be used as base classes for extensions by the user. Richer implementations are also provided to serve as defaults; for polyhedra they provide all optional incidences, a three-dimensional point in the vertex type and a plane equation in the face type.
The Halfedge data structure concept HalfedgeDS, is responsible for the storage organization of the items. Currently, implementations using internally a bidirectional list or a vector are provided. The HalfedgeDS defines the handles and iterators belonging to the items. These types are promoted to the declaration of the items themselves and are used there to provide the references to the incident items. This promotion of types is done with a template parameter Refs of the item types. The halfedge data structure provides member functions to insert and delete items, to traverse all items, and it gives access to the items.
There are two different models for the HalfedgeDS concept available, HalfedgeDS_list and HalfedgeDS_vector, and more might come. Therefore we have kept their interface small and factored out common functionality into separate helper classes, HalfedgeDS_decorator, HalfedgeDS_const_decorator, and HalfedgeDS_items_decorator, which are not shown in Figure 28.1, but would be placed at the side of the HalfedgeDS since they broaden that interface but do not hide it. These helper classes contain operations that are useful to implement the operations in the next layer, for example, the polyhedron. They add, for example, the Euler operations and partial operations from which further Euler operations can be built, such as inserting an edge into the ring of edges at a vertex. Furthermore, the helper classes contain adaptive functionality. For example, if the HalfedgeDSHalfedge::prev() member function is not provided for halfedges, the HalfedgeDS_items_decorator::find_prev() member function of a helper class searches in the positive direction along the face for the previous halfedge. But if the HalfedgeDSHalfedge::prev() member function is provided, the HalfedgeDS_items_decorator::find_prev() member function simply calls it. This distinction is resolved at compile time with a technique called compile-time tags, similar to iterator tags in [8].
The Polyhedron_3 as an example for the third layer adds the geometric interpretation, provides an easy-to-use interface of high-level functions, and unifies the access to the flexibility provided underneath. It renames face to facet, which is more common for three-dimensional surfaces. The interface is designed to protect the integrity of the internal representation, the handles stored in the items can no longer directly be written by the user. The polyhedron adds the convenient and efficient circulators, see Circulator, for accessing the circular sequence of edges around a vertex or around a facet. To achieve this, the Polyhedron_3 derives new vertices, halfedges and facets from those provided in Items. These new items are those actually used in the HalfedgeDS, which gives us the coherent type structure in this design, especially if compared to our previous design.
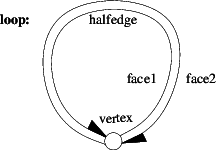
The following example program uses the default halfedge data structure and the decorator class. The default halfedge data structure uses a list-based representation. All incidences of the items and a point type for vertices are defined. The trivial traits class provides the type used for the point. The program creates a loop, consisting of two halfedges, one vertex and two faces, and checks its validity.
File HalfedgeDS/hds_prog_default.cpp
The following program defines a minimal halfedge data structure using the minimal items class HalfedgeDS_min_items and a list-based halfedge data structure. The result is a data structure maintaining only halfedges with next and opposite pointers. No vertices or faces are stored. The data structure represents an undirected graph.
File HalfedgeDS/hds_prog_graph.cpp
The default halfedge data structure uses a list internally and the maximal base classes. We change the list to a vector representation here. Again, a trivial traits class provides the type used for the point. Note that for the vector storage the size of the halfedge data structure should be reserved beforehand, either with the constructor as shown in the example or with the reserve() member function. One can later resize the data structure with further calls to the reserve() member function, but only if the data structure is in a consistent, i.e., valid, state.
File HalfedgeDS/hds_prog_vector.cpp
This example reuses the base class available for faces and adds a member variable color.
File HalfedgeDS/hds_prog_color.cpp
The halfedge data structure as presented here is slightly less space efficient as, for example, the winged-edge data structure [1], the DCEL [7] or variants of the quad-edge data structure [4]. On the other hand, it does not require any search operations during traversals. A comparison can be found in [5].
The following example trades traversal time for a compact storage representation using traditional C techniques (i.e., type casting and the assumption that pointers, especially those from malloc or new, point to even addresses). The idea goes as follows: The halfedge data structure allocates halfedges pairwise. Concerning the vector-based data structure this implies that the absolute value of the difference between a halfedge and its opposite halfedge is always one with respect to C pointer arithmetic. We can replace the opposite pointer by a single bit encoding the sign of this difference. We will store this bit as the least significant bit in the next halfedge handle. Furthermore, we do not implement a pointer to the previous halfedge. What remains are three pointers per halfedge.
We use the static member function HalfedgeDS::halfedge_handle() to convert from pointers to halfedge handles. The same solution can be applied to the list-based halfedge data structure HalfedgeDS_list, see examples/HalfedgeDS/hds_prog_compact2.cpp. Here is the example for the vector-based data structure.
File HalfedgeDS/hds_prog_compact.cpp
Two edges are created in the default halfedge data structure. The halfedge iterator is used to count the halfedges.
File HalfedgeDS/hds_prog_halfedge_iterator.cpp
Three edges are created in the default halfedge data structure. The adapter N_step_adaptor is used to declare the edge iterator used in counting the edges.
File HalfedgeDS/hds_prog_edge_iterator.cpp