|
CGAL 6.1 - Optimal Bounding Box
|
|
CGAL 6.1 - Optimal Bounding Box
|
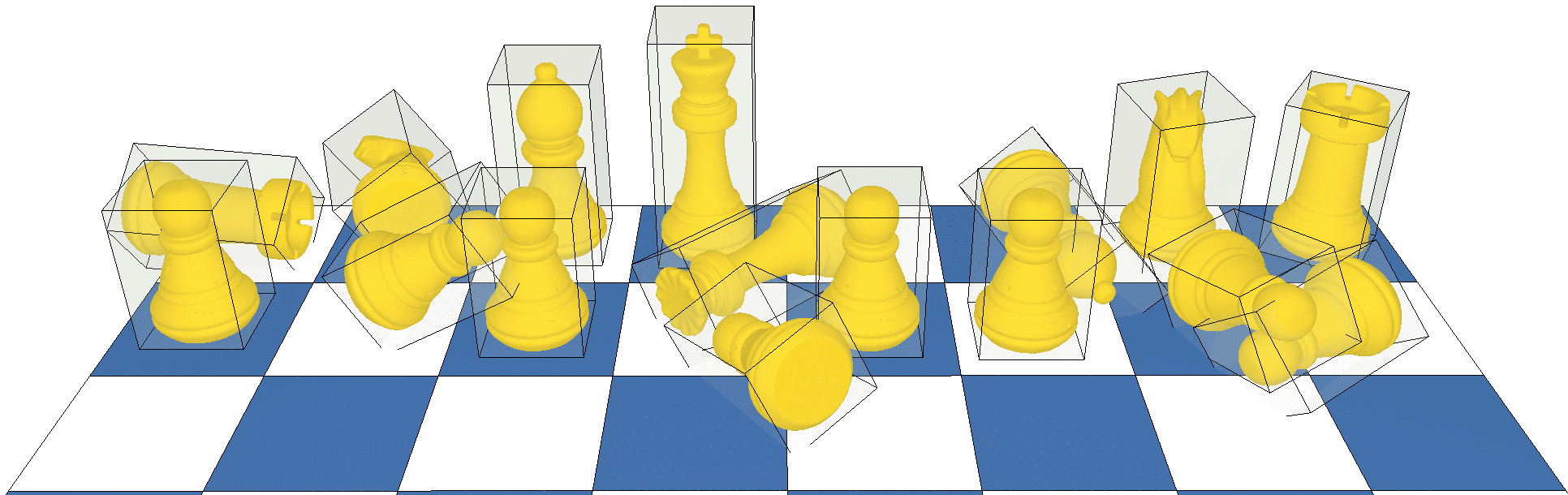
Encompassing a model within a volume is a common approach to accelerate a number of applications such as collision detection or visibility testing: the proxy volume provides a rapid way to test a configuration or filter results, with the real model only being used when required. Typical coarser volumes that can be used to approximate a more complex model are simplified meshes (for example using the package Triangulated Surface Mesh Simplification), convex hulls, or simple rectangular boxes. Within this last category, the axis-aligned bounding box (AABB) has obvious advantages: it is extremely simple to compute and one may build a hierarchical structure of successively tighter volumes to further speed up intersection and distance computations. One such example of structure is the CGAL AABB tree (2D and 3D Fast Intersection and Distance Computation). The disadvantage is also clear: the box is usually poorly fitting most models. A good compromise between the good approximation offered by convex hulls or simplified meshes and the speed offered by axis-aligned bounding boxes are Optimal Bounding Boxes. Contrary to the AABB, the optimal bounding box of a model is not necessarily axis-aligned, but provides a tight approximation.

Figure 106.2 Left: the axis-aligned bounding box. Right: the optimal bounding box, a much better fit.
In 2D, the optimal bounding rectangle of an input can be computed in linear time using the technique of rotating calipers, first introduced by Toussaint [4] (see also the CGAL package Bounding Volumes). An algorithm to compute the optimal oriented bounding box in 3D was proposed by O’Rourke [3], but its cubic complexity in the number of points makes it unusable in practice. The implementation proposed in this package is based on the paper of Chang et al.[1], who introduced an algorithm to compute a close approximation of the optimal bounding box. As this is but an approximation of the optimal bounding box, we call the resulting box, the Oriented Bounding Box.
The algorithm introduced by Chang et al. formulates the computation of the optimal bounding box as an unconstrained optimization problem on the 3D matrix rotation group. The function to optimize is defined as the volume of the box. Because this function is non-differentiable, in particular near local optima, traditional optimization methods might encounter convergence issues. Consequently, Chang et al.'s algorithm employs a combination of a derivative-free optimization method, the Nelder-Mead simplex method [2], and a metaheuristics method based on biological evolution principles to maintain and evolve a population of tentative rotation matrices. The purpose of this evolution is to oppose a global approach to the local Nelder-Mead optimization, enabling the algorithm to explore the search space as much as possible, and to find not only a local minimum, but a global optimum.
In theory, the genetic algorithms used by Chang et al. enable - given enough time - the algorithm to explore the complete search space. In practice, an algorithm does not have infinite time at its disposal. In addition, there is no simple way to check if the current-best solution is optimal. Thus, an implementation of the algorithm cannot provide the same guarantees that the theoretical algorithm offers. However, we observe that in practice the algorithm constructs a close approximation of the optimal bounding box most of the time.
As the bounding box only depends on the convex hull of the object, computing its convex hull as a preprocessing step is a good way to reduce the number of points in subsequent computations. The computational trade-off is developed in more details in Section Complexity and Performance.
The computation of the oriented bounding box can be performed by calling the free function CGAL::oriented_bounding_box(). Convex hull computation is performed using the package 3D Convex Hulls, and is enabled by default.
The input can be a range of 3D points, or a mesh, with a variety of Named Parameters enabling using further custom inputs.
The result of the algorithm can be retrieved as:
CGAL::make_hexahedron() , which can be used to construct a mesh from these points.MutableFaceGraph, a quadrangular mesh representing the oriented bounding box.The requirements on geometric objects and operations on these objects are described in the traits class concept OrientedBoundingBoxTraits_3. A model of this concept is provided: CGAL::Oriented_bounding_box_traits_3.
If the approach using the convex hull is chosen, a kernel offering exact predicates must be used to ensure a correct hull. In addition, the eight bounding vertices are constructed using the best found affine transformation; consequently, a kernel providing exact construction may also be useful.
A major drawback of the exact algorithm of O’Rourke is its cubic complexity and consequent large runtimes. In this section, we investigate the speedup gained by preprocessing the input data with a convex hull computation, and show that the oriented bounding box algorithm exhibits linear complexity.
Models from the Thingi10k data set are used with speeds being averaged over 100 runs for each model. The machine used is a laptop running Fedora 30 64-bits, with two 6-core Intel(R) i9-8950HK CPU clocked at 2.90GHz, and with 32GB of RAM. The CGAL kernel used is CGAL::Exact_predicates_inexact_constructions_kernel.
Computing the convex hull as a preliminary step provides a significant speed advantage.
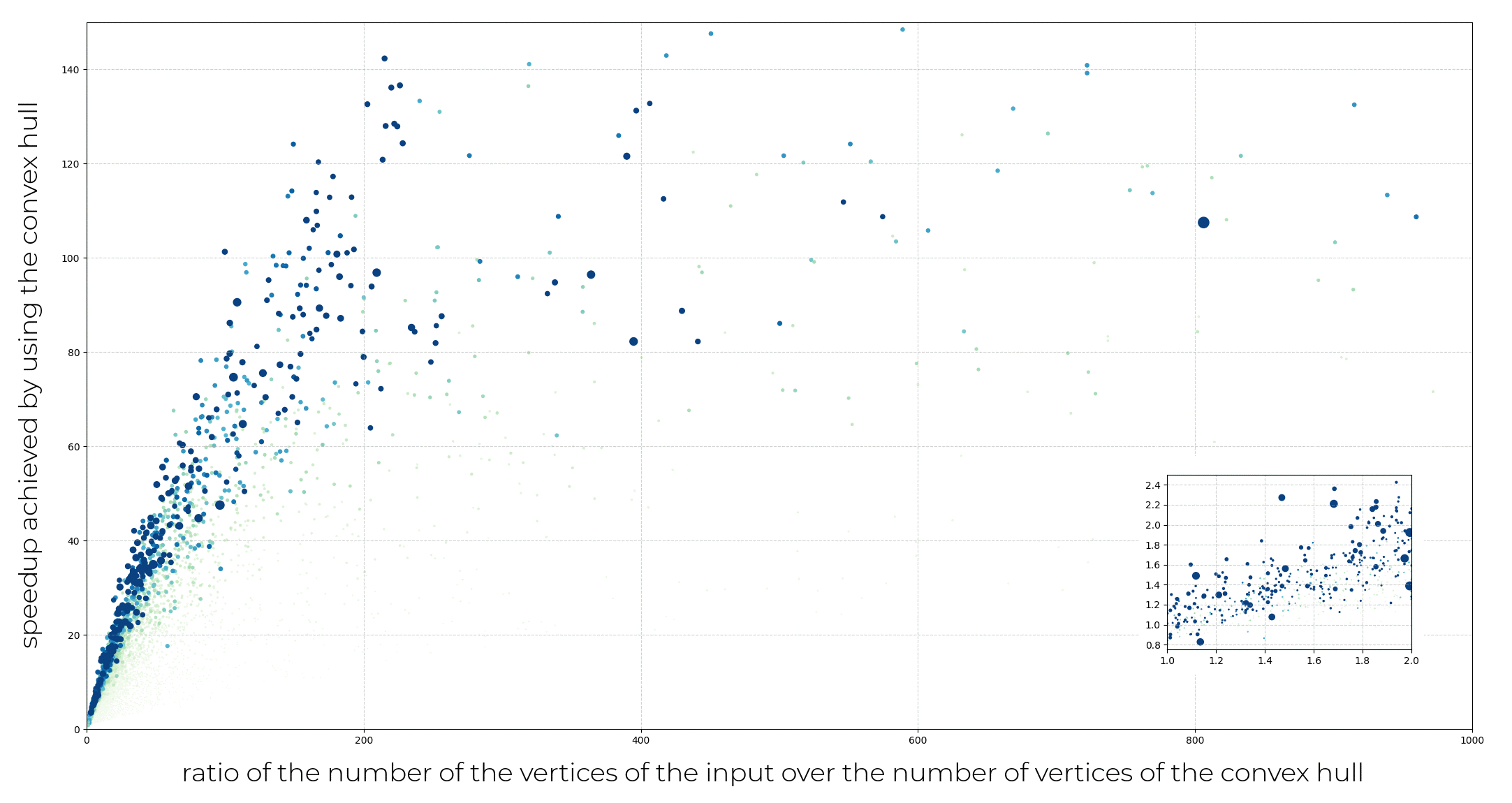
Figure 106.3 Computation of the speedup achieved on the total runtime of the algorithm when the convex hull is computed and used afterwards. Note that the total runtime includes the construction of the convex hull (when it is used). The color and size of the dots represent the number of vertices in the input data (larger, bluer points having more input vertices than greener, smaller points). Computing the convex hull is beneficial for all but a handful of cases.
We analyze in this section the computation time of the algorithm based on the number of vertices on the convex hull.
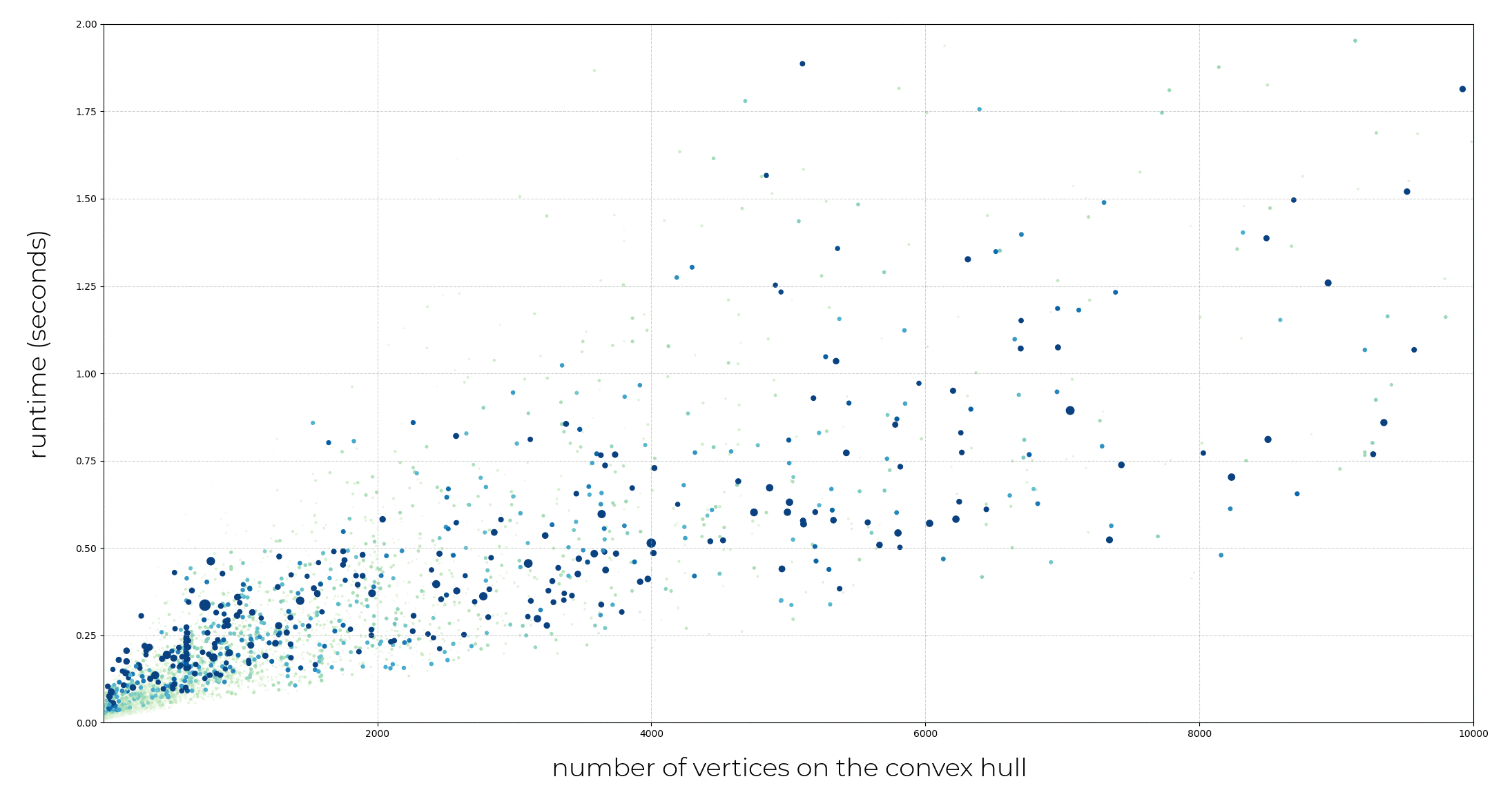
Figure 106.4 Running times for the oriented bounding box construction of the convex hull of models of the Thingi10k data set. The color and size of the dots represent the number of vertices in the input data (larger, bluer points having more input vertices than greener, smaller points). The algorithm exhibits linear complexity in practice. For visibility reasons, the few models whose convex hull has more than 10000 vertices are excluded from this graph, but consistent results are observed.
The following example illustrates a basic usage of the algorithm: an input mesh is read, its oriented bounding box is computed using an array as output, and a mesh is constructed from the eight points.
File Optimal_bounding_box/obb_example.cpp
The following example illustrates how to use Named Parameters to efficiently compute the oriented bounding box of a mesh whose vertices' positions are modified on the fly.
File Optimal_bounding_box/obb_with_point_maps_example.cpp
The following example uses the affine transformation, which is the affine transformation such that the axis-aligned bounding box of the transformed vertices of the mesh has minimum volume, returned by the algorithm to build a custom vertex point property map. An AABB tree of the (on the fly) rotated faces of the mesh is then constructed.
File Optimal_bounding_box/rotated_aabb_tree_example.cpp
A prototype was created by Konstantinos Katrioplas in 2018. Mael Rouxel-Labbé worked to speed up and robustify the implementation, and to submit the first version of this package.